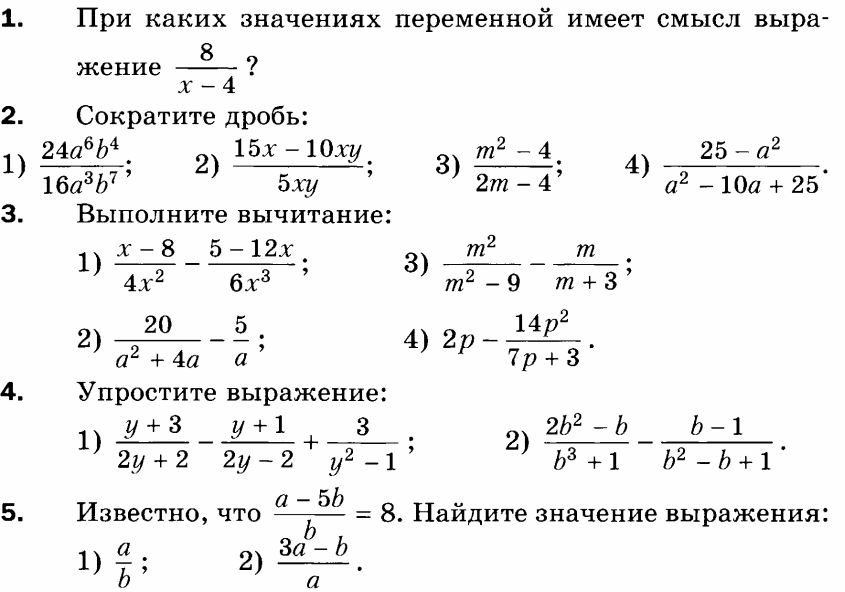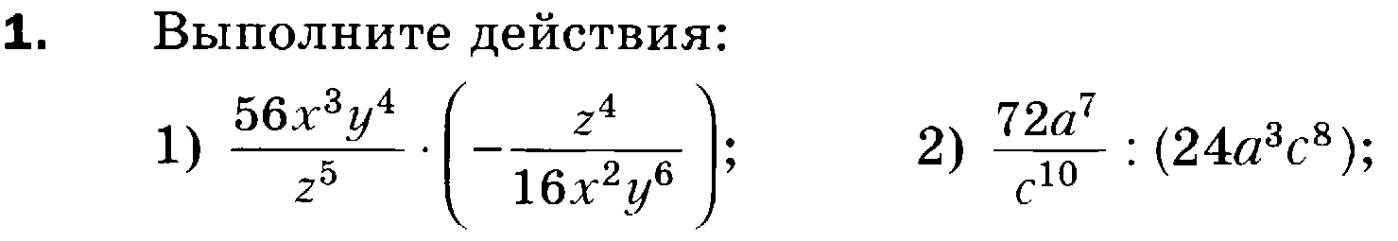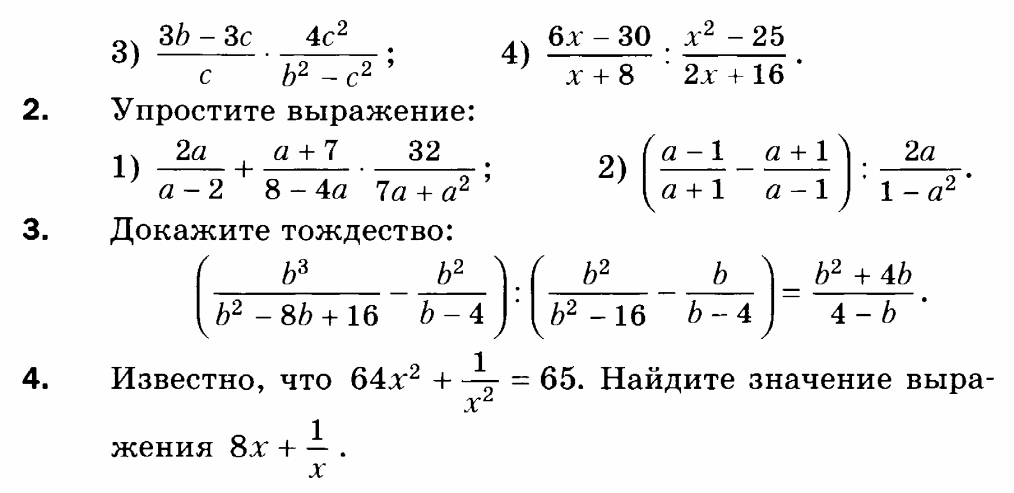СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ

Благодаря готовым учебным материалам для работы в классе и дистанционно

Выбрать материалы

Скидки до 50 % на комплекты
только до 15.05.2025

Готовые ключевые этапы урока всегда будут у вас под рукой

Организационный момент

Проверка знаний

Объяснение материала

Закрепление изученного

Итоги урока

Обо мне Блог Файлы Тесты Галерея Активность Награды

Контрольно-измерительные материалы по математике 8 класс

Категория: Математика

Нажмите, чтобы узнать подробности

Тексты контрольных работ по алгебре и геометрии 8 класс с ответами

Просмотр содержимого документа
«Контрольно-измерительные материалы по математике 8 класс»

Приложение

к рабочей программе по математике базового уровня















КОНТРОЛЬНО-ОЦЕНОЧНЫЕ СРЕДСТВА


по математике

8 класс






















Контрольно-оценочные средства

Структура и содержание


  1. Паспорт КОС


Раздел, тема

Проверяемые компетенции (из рабочей программы)

Вид оценочных средств (контрольная работа, тест, диктант, тестирование в формате ОГЭ, ЕГЭ и т.д.)

Вариативность

8 класс; алгебра

Рациональные выражения

Рациональные дроби. Основное свойство рациональных дробей. Сложение и вычитание рациональных дробей с одинаковыми знаменателями. Сложение и вычитание рациональных дробей с разными знаменателями. Умножение и деление рациональных дробей. Возведение в степень рациональных дробей. Тождественное преобразование рациональных выражений. Равносильные уравнения. Рациональные уравнения. Степень с целым отрицательным показателем. Свойства степени с целым показателем. Функция y=k/x и её график.

Контрольные работы «Сложение и вычитание рациональных дробей с разными знаменателями», «Тождественные преобразования рациональных выражений», «Рациональные уравнения. Функция k/x и её график»

2

Квадратные корни. Действительные числа

Функция y= x² и её график. Квадратные корни. Арифметический квадратный корень. Множество и его элементы. Подмножество. Операции над множествами. Числовые множества. Свойства арифметического квадратного корня. Тождественное преобразование выражений, содержащих арифметические квадратные корни. Функция y=√x и её график.

Контрольные работы «Тождественные преобразования выражений, содержащих квадратные корни. Функция y=x² и её график».

2

Квадратные уравнения

Квадратные уравнения. Решение неполных квадратных уравнений. Формула корней квадратного уравнения. Теорема Виета. Квадратный трёхчлен. Решение уравнений, сводящихся к квадратным уравнениям. Рациональные уравнения как математические модели реальных ситуаций.

Контрольные работы: «Квадратные уравнения», «Рациональные уравнения»

2

Повторение и систематизация учебного материала

Задачи на обобщение и систематизацию знаний. Проверяются умения к обобщению и систематизации знаний по основным темам курса алгебры 8 класса

Итоговая контрольная работа

2

8 класс, геометрия

Четырехугольники

Четырёхугольник и его элементы. Параллелограмм. Свойства параллелограмма. Признаки параллелограмма. Прямоугольник. Ромб. Квадрат. Средняя линия треугольника. Трапеция. Центральные и вписанные углы. Описанная и вписанная окружности четырёхугольника

Контрольные работы «Параллелограмм. Прямоугольник. Ромб. Квадрат», «Средняя линия треугольника. Трапеция. Центральные и вписанные углы. Описанная и вписанная окружности четырёхугольника»

2

Подобные треугольники

Теорема Фалеса. Теорема о пропорциональных отрезках. Подобные треугольники. Первый признак подобия треугольников. Второй и третий признаки подобия треугольников.

Контрольные работы «Теорема Фалеса. Теорема о пропорциональных отрезках. Признаки подобия треугольников.»

2

Решение прямоугольных треугольников.

Метрические соотношения в прямоугольном треугольнике. Теорема Пифагора. Тригонометрические функции острого угла прямоугольного треугольника. Решение прямоугольных треугольников

Контрольные работы «Метрические соотношения в прямоугольном тре-угольнике. Теорема Пифагора», «Тригонометрические функции острого угла прямоугольного треугольника. Решение прямоугольных треугольников».

2

Многоугольники. Площадь многоугольника.

Многоугольники. Понятие площади многоугольника. Площадь прямоугольника. Площадь параллелограмма. Площадь треугольника. Площадь треугольника.

Контрольная работа «Многоугольники. Площадь многоугольника»

2

Повторение

Задачи на обобщение и систематизацию знаний. Проверяются умения к обобщению и систематизации знаний по основным темам курса геометрии 8 класса

Итоговая контрольная работа

2


  1. КИМ с критериями оценки

Отметка «5» ставится, если:

  1. работа выполнена полностью;

  2. в логических  рассуждениях и обосновании решения нет пробелов и ошибок; 

  3. в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непо­нимания учебного материала).


Отметка «4» ставится, если:

  1. работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

  2. допущена одна ошибка или два-три недочета в выкладках, ри­сунках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки).


 Отметка «3» ставится, если:

допущены более одной ошибки или более двух-трех недоче­тов в выкладках, чертежах или графиках, но учащийся владеет обязательными умениями по проверяемой теме.


Отметка «2» ставится, если:

допущены существенные ошибки, показавшие, что учащийся не владеет обязательными умениями по данной теме в полной мере.




Перечень ошибок


К    грубым    ошибкам относятся ошибки, которые обнаруживают незнание учащимися формул, правил, основных свойств, теорем и неумение их применять; неумение преобразовывать выражения с квадратными корнями; неумение решать квадратные и другие виды уравнений; незнание приемов решения задач, рассматриваемых в учебниках, а также вычислительные ошибки, если они не являются опиской; неумение читать и строить графики.

К    негрубым   ошибкам относятся: неправильное списывание данных, чисел, знаков; неточности формулировок, определений, понятий; недоведение преобразований до конца.

  •  

К    недочетам    относятся: недостаточность или отсутствие пояснений, обоснований в решениях; нерациональные записи при вычислениях, нерациональные приемы вычислений, преобразований и решений задач; отдельные погрешности в формулировке вопроса или ответа; небрежное выполнение записей, чертежей, схем, графиков; орфографические и пунктуационные ошибки.





Контрольные работы по алгебре

8класс

Контрольная работа «Сложение и вычитание рациональных дробей с разными знаменателями»

Вариант 1




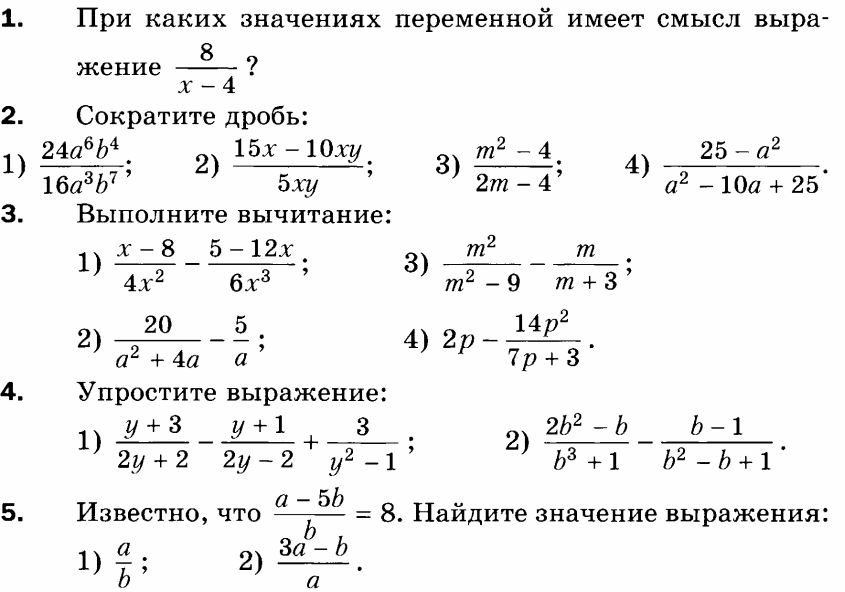
Вариант 2

Ответы.

Вариант 1: 1.все х, кроме х=4; 2. 1)3a³/2b³, 2)3-2y/y, 3)m+2/2, 4) 5+a/5-a;3. 1)3x²-10/12x³,

2)-5/a+4, 3)3m/m²-9, 4)6p/7p+3;4.1)1/y²-1, 2)1/b+1; 5. 1)13, 2)2 12/13.

Вариант 2: 1.все х, кроме х=-11; 2. 1)2a⁴/3b⁴, 2)2n-3/n, 3)3/c-5; 3. 1)15x²-8/18x³, 2)-6/b+4, 3)4c/c²-16, 4)3y/6y+1; 4. 1)1/y²-4,2)3b/b+4; 5. 1)6; 2)65/6


Контрольная работа «Тождественные преобразования рациональных выражений»

Вариант 1

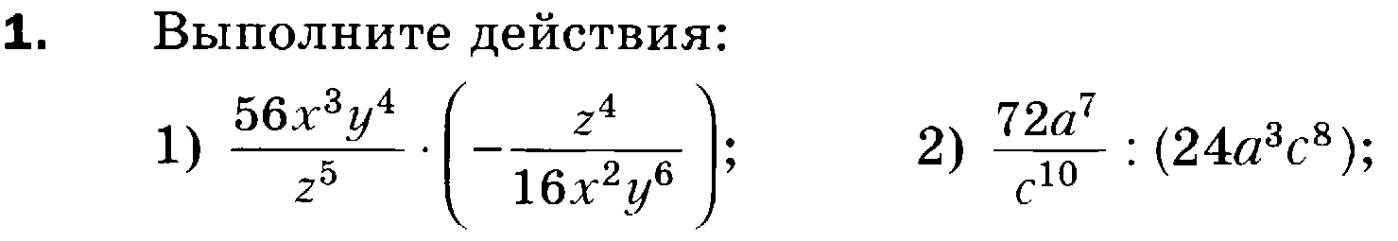
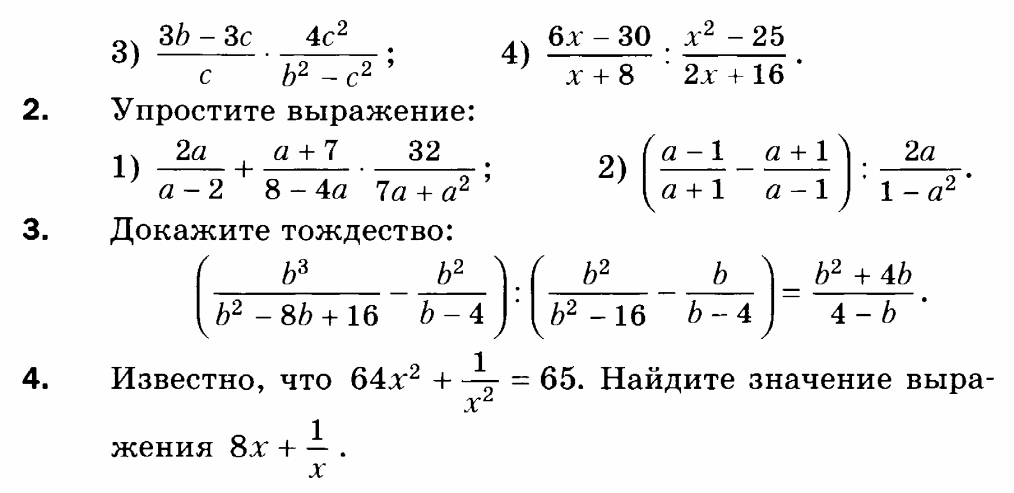
Вариант 2


Ответы.

Вариант 1:1. 1)-7x/2zy², 2)3a⁴/c¹8, 3)12c/b+c, 4)12/x+5; 2. 1)2(a+2)/a, 2)2; 3. Тождество доказано; 4.-9 и 9.

Вариант 2:1. 1)9a²c8/2b6, 2)2m³/p19, 3)30b/a-b, 4)x-7/15; 2/1)3(a+3)/a, 2)-1/3; 3. Тождество доказано; 4. -6 и 6.


Контрольная работа «Рациональные уравнения. Функция k/x и её грфик».

Вариант 1

















Вариант 2



Ответы.

Вариант 1: 1. 1)4, 2) 5; 2. 1)1,26·10⁵, 2)3,5·10-3; 2. 1)a², 2)a³, 3)a²; 4.0,96a³b²; 5.1)7/24, 2)1/49;6.5b²/64a³; 7.1)1/36, 2)-3; 8. Построен график, 8;9. 1)-1;0, 2)4

Вариант 2:1. 1)-4, 2)-4; 2. 1) 2,45·10⁵, 2)1,9 ·10-3; 3. 1) a², 2)a², 3)a; 4. 0,34a²b²; 5. 1)17/36, 2)1/8; 6. a²/12b20; 7. 1)1/9, 2)1/8; 8. Построен график, 2;3; 9.1)-1 или 0, 2)2.


Контрольная работа «Тождественные преобразования выражений, содержащих квадратные корни. Функция y=x² и её график»

Вариант 1


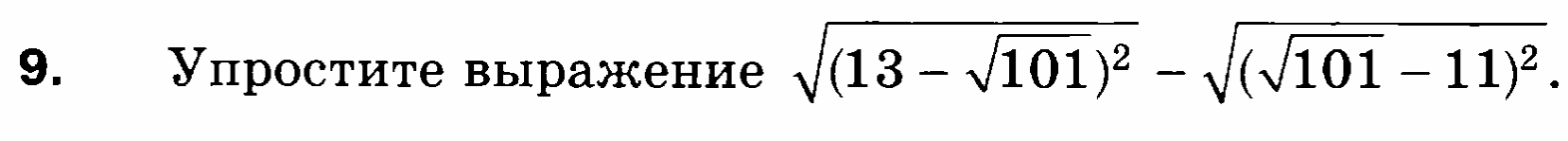
Вариант 2


Ответы.

Вариант 1: 1.A∩B{2;3;6}, AUB{2;3;4;6;8;9;12;18;24}; 2. 1)18, 2)4,5, 3)96, 4)7; 3. ±√2, 2)нет решений, 3)16, 4)нет решений. 4.1)13√2б 2)10 3)49-12√5 4)-33; 5. 1)a-7 2)√33-1 3) √a-√3/√a+√3; 7. 1) √6/4 2)√14+2 8. 1)-b√5 2)a²√12 3)‌‌‌‌|a²|√-a 4)-ab³√-a; 9. 2

Вариант 2: 1.A∩B{2;3;6}, AUB{2;3;4;5;6;10;12;15;30 }; 2. 1)7, 2)5,6, 3)72, 4)18; 3. ±√5, 2)нет решений, 3)81, 4)нет решений. 4.1)18√3, 2)30 3)37-12√7 4)71; 5. 1)a+8 2)1-√11 3) √a-√5/√a+√5; 7. 1) 4√2/3 2)√13+3 8. 1)-a√11 2)3a⁴√2 3)‌‌‌‌|a³|√-a 4)-a⁵b²√-b; 9. 3



Контрольная работа «Квадратные уравнения»

Вариант 1

_________________________________________________________________

Вариант 2

Ответы.

Вариант 1: 1. 1)±√3 2)0; -1,8 3)-7; 6 4)9; 1/3 5) нет решений 6)1/4; 2.x²+10x +8=0 3.12см и

16 см 4. X2=-0,5 c=3 5.3 6.132

Вариант 2: 1. 1)±√5 2)0; -5/3 3)8; -3 4)3; 1/7 5) нет решений 6)-1,5; 2.x²-6x +4=0; 3.12см и

9см 4. X2=1/3 b=-13 5.8; 6.108




Контрольная работа «Рациональные уравнения»

Вариант 1

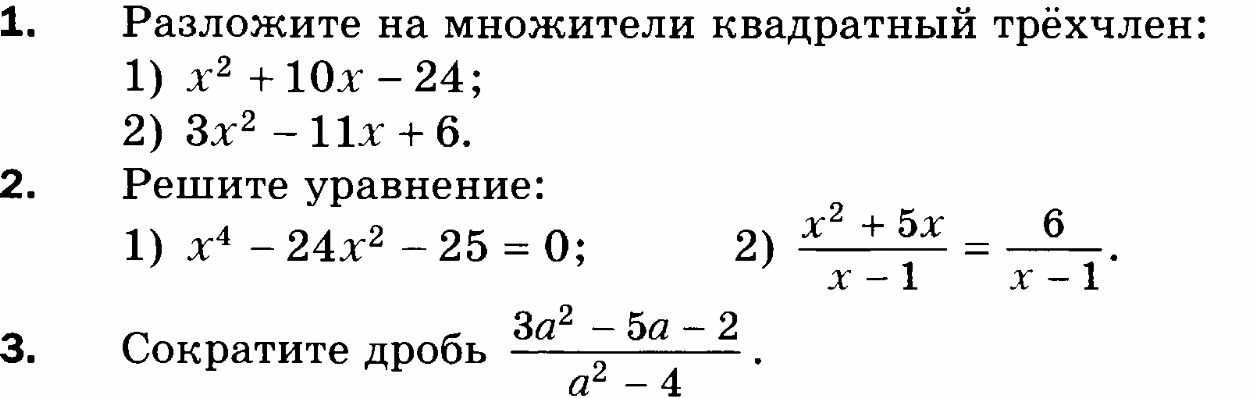
Вариант 2

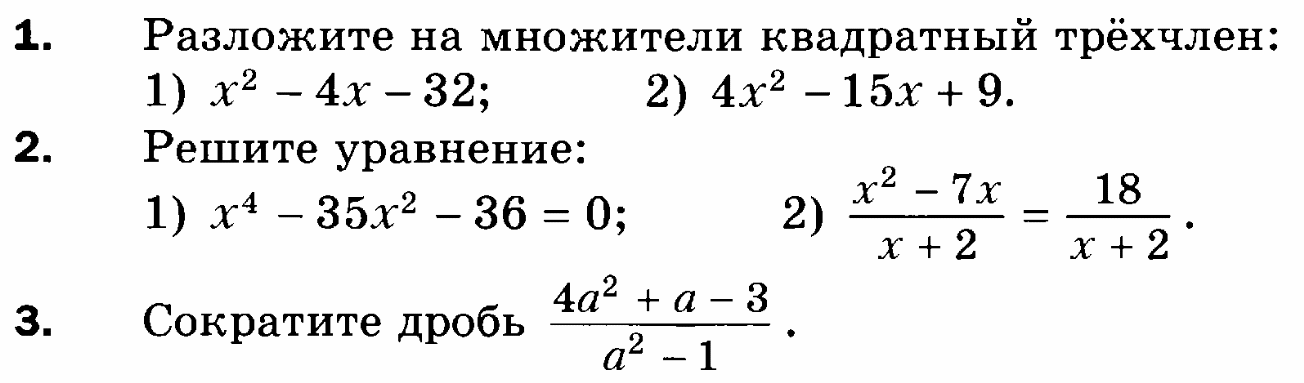
Ответы.

Вариант 1: 1. 1) (x+12)(x-2); 2)(3x-2)(x-3); 2. 1) -5; 5 2)-6 3. 2; -1/3; 4.9; 5.60 км/ч, 40 км/ч

6. Построен график.

Вариант 2: 1. 1) (x-8)(x+4); 2)(4x-3)(x-3); 2. 1) -3; 3 2)9; 3. 3/4; -1; 4. 15; 5.60 км/ч, 50 км/ч

6. Построен график.



Итоговая контрольная работа

Вариант 1



Вариант 2

Ответы.

Вариант 1: 1. 5n6/2m; 2)1/m4; 3)7√a; 4.(-∞; 1/3)U(1/3; 3)U(3; +∞); 5.-2/a+5; 6. 16деталей,20 деталей; 7.Построен график. 8. Доказательство проведено.

Вариант 2: 1. 3a²/2b6; 2)n³; 3)√6; 4.(-∞; 3/2)U(3/2; 2)U(2; +∞); 5.2/b-4; 6.20м³,30 м³; 7.Построен график. 8. Доказательство проведено.



Контрольные работы по геометрии.


Контрольная работа по теме «Параллелограмм. Прямоугольник. Ромб. Квадрат»

Вариант 1

1. Одна из сторон параллелограмма в 5 раз больше другой, а его периметр равен 36 см. Найдите стороны параллелограмма.

2. В прямоугольнике АВСD диагонали пересекаются в точке О, АD = 14 см, ВD = 18 см. Найдите периметр треугольника ВОС.

3. Сторона ромба образует с одной из его диагоналей угол 68°. Найдите углы ромба.

4. На диагонали АС параллелограмма АВСD отметили точки Р и К так, что АР = СК (точка Р лежит между точками А и К). Докажите, что ∠АDР = ∠СВК.

5. В параллелограмме АВСD биссектриса угла D пересекает сторону АВ в точке Р. Отрезок АР меньше отрезка ВР в 6 раз. Найдите периметр параллелограмма, если АВ = 14 см.

6. Прямая, пересекающая диагональ ВD параллелограмма АВСD в точке Е, пересекает его стороны АВ и СD в точках М и К соответственно, причем МЕ = КЕ. Докажите, что четырехугольник ВКDМ – параллелограмм.


Вариант 2.

1. Одна из сторон параллелограмма в 5 раз больше другой, а его периметр равен 36 см. Найдите стороны параллелограмма.

2. В прямоугольнике АВСD диагонали пересекаются в точке О, АD = 14 см, ВD = 18 см. Найдите периметр треугольника ВОС.

3. Сторона ромба образует с одной из его диагоналей угол 68°. Найдите углы ромба.

4. На диагонали АС параллелограмма АВСD отметили точки Р и К так, что АР = СК (точка Р лежит между точками А и К). Докажите, что ∠АDР = ∠СВК.

5. В параллелограмме АВСD биссектриса угла D пересекает сторону АВ в точке Р. Отрезок АР меньше отрезка ВР в 6 раз. Найдите периметр параллелограмма, если АВ = 14 см.

6. Прямая, пересекающая диагональ ВD параллелограмма АВСD в точке Е, пересекает его стороны АВ и СD в точках М и К соответственно, причем МЕ = КЕ. Докажите, что четырехугольник ВКDМ – параллелограмм.


Ответы. Вариант 1. 1. АВ = 3 см; ВС = 15 сь ;2. Р = 32 см;3. ∠А = 136°; ∠В = 44°;4. Доказательство;5. Р = 32 см;6. Доказательство

Вариант2. 1. АВ = 3 см; ВС = 15 см; 2. Р = 32 см; 3. ∠А = 136°; ∠В = 44°;4. Доказательство;5. Р = 32 см; 6. Доказательство


Контрольная работа по теме «Средняя линия треугольника. Трапеция. Центральные и вписанные углы. Описанная и вписанная окружности четырёхугольника»

Вариант 1

1. Найдите периметр треугольника, если его средние линии равны 6 см, 9 см и 10 см.

2. Основания трапеции относятся как 3 : 5, а средняя линия равна 32 см. Найдите основания трапеции.

3. Боковые стороны трапеции равны 7 см и 12 см. Чему равен периметр трапеции, если в неё можно вписать окружность?

4. Основания равнобокой трапеции равны 3 см и 7 см, а диагональ делит тупой угол трапеции пополам. Найдите периметр трапеции.

5. Найдите углы четырёхугольника ABCD, вписанного в окружность, если ∠ADB = 43°, ∠ACD = 37°, ∠CAD = 22°.

6. Высота равнобокой трапеции равна 9 см, а её диагонали перпендикулярны. Найдите периметр трапеции, если её боковая сторона равна 12 см.

Вариант 2

1. Стороны треугольника равны 10 см, 12 см и 14 см. Найдите периметр треугольника, вершины которого — середины сторон данного треугольника.

2. Основания трапеции относятся как 4 : 7, а средняя линия равна 44 см. Найдите основания трапеции.

3. Основания трапеции равны 6 см и 12 см. Чему равен периметр трапеции, если в неё можно вписать окружность?

4. Основания равнобокой трапеции равны 8 см и 10 см, а диагональ делит острый угол трапеции пополам. Найдите периметр трапеции.

5. Найдите углы четырёхугольника ABCD, вписанного в окружность, если ∠CBD = 48°, ∠ACD = 34°, ∠BDC = 64°.

6. Высота равнобокой трапеции равна 10 см, а её диагонали перпендикулярны. Найдите боковую сторону трапеции, если её периметр равен 48 см.


Ответы:

Вариант 1 :1.   Р = 50 см.2.   ВС = 24 см; AD = 40 см.3.   Р = 38 см.4.   Р = 16 см.5.   ∠А = 100°, ∠B = 59°, ∠C = 80°, ∠D = 121°.6.   Р = 42 см.

Вариант 2: 1. Р = 18 см; 2. ВС = 32 см; AD = 56 см; 3. Р = 36 см;4. Р = 34 см;5. ∠А = 112°, ∠B = 82°, ∠C = 68°, ∠D = 98°;6. АВ = 14 см.




Контрольная работа по теме «Теорема Фалеса. Теорема о пропорциональных отрезках. Признаки подобия треугольников»


Вариант 1.

  1. На рисунке 124 АВ || CD, МА = 12 см, АС = 4 см, BD = б см. Найдите отрезок МВ.

  2. Треугольники АВС и А1В1С1 подобны, причём сторонам АВ и ВС соответствуют стороны А1В1 и В1С1. Найдите неизвестные стороны этих треугольников, если АВ = 8 см, ВС = 10 см, А1В1 = 4 см, А1С1 = 6 см.

  3. Отрезок АК — биссектриса треугольника АВС, АВ = 12 см, ВК = 8 см, СК = 18 см. Найдите сторону АС.

  4. На стороне ВС треугольника АВС отметили точку М так, что ВМ : МС = 2 : 9. Через точку М провели прямую, которая параллельна стороне АС треугольника и пересекает сторону АВ в точке К. Найдите сторону АС, если МК = 18 см.

  5. В трапеции ABCD с основаниями AD и ВС диагонали пересекаются в точке О, ВС : AD = 3 : 5, BD = 24 см. Найдите отрезки ВО и OD.

  6. Через точку М, находящуюся на расстоянии 15 см от центра окружности радиусом 17 см, проведена хорда, которая делится точкой М на отрезки, длины которых относятся как 1 : 4. Найдите длину этой хорды.

Вариант 2.

  1. Стороны угла О пересекают параллельные прямые PK и NM, (точка P между O и N), NP=20 см, PO=8 см, MK=15 см. Найдите отрезок KO.

  2. Треугольники АВС и А1 В1 С1 подобны, причем сторонам АВ и ВС соответствуют стороны А1 В1 и В1 С1. Найдите неизвестные стороны этих треугольников, если ВС=5 см, АВ=6 см, В1С1=15 см, А1 С1=21 см.

  3. Отрезок CD – биссектриса треугольника АВС, АС=12 см, ВС=18 см, AD=10 см. Найдите отрезок BD.

  4. На стороне АВ треугольника АВС отметили точку Е так, что АЕ : ВЕ= 3:4. Через точку Епровели прямую, которая параллельна стороне АС треугольника и пересекает сторону ВСв точке F. Найдите отрезок EF, если АС =28 см.

  5. В трапеции АВСD с основаниями АD и ВС диагонали пересекаются в точке О, ВО : ОD = 2:3, АС=25 см. Найдите отрезки АО и ОС.

  6. Через точку Р, лежащую внутри окружности, проведена хорда, которая делится точкой Рна отрезки, длины которых равны 4 см и 5 см. Найдите расстояние от точки Р до центра окружности, если её радиус равен 6 см.



Ответы:

Вариант 1: 1. МВ = 18 см; 2. АС = 12 см; В1С1 = 5 см;3. АС = 27 см;4. АС = 99 см;5. ВО = 9 см; OD = 15 см;6. АВ = 20 см.

Вариант 2: 1. КО = 6 см;2. АС = 7 см; А1В1 = 18 см;3. BD = 15 см;4. EF = 16 см;5. СО = 10 см; АО = 15 см;6. ОР = 4 см.

Контрольная работа по теме «Метрические соотношения в прямоугольном тре-угольнике. Теорема Пифагора»

Вариант 1.

  1. Высота прямоугольного треугольника, проведённая к гипотенузе, делит её на отрезки длиной 9 см к 16 см. Найдите меньший катет треугольника.

  2. В прямоугольном треугольнике гипотенуза равна 13 см, а один из катетов — 12 см. Найдите периметр треугольника.

  3. Диагонали ромба равны 12 см и 16 см. Найдите сторону ромба.

  4. Высота ВМ равнобедренного треугольника АВС (АВ = АС) делит сторону АС на отрезки AM = 15 см и СМ = 2 см. Найдите основание треугольника АВС.

  5. Из точки к прямой проведены две наклонные, проекции которых на прямую равны 9 см и 16 см. Найдите расстояние от точки до прямой, если одна из наклонных на 5 см больше другой.

  6. Окружность, вписанная в прямоугольную трапецию, делит точкой касания большую боковую сторону на отрезки длиной 4 см и 25 см. Найдите высоту трапеции.

Вариант 2.

  1. Катет прямоугольного треугольника равен 30 см, а его проекция на гипотенузу – 18 см. Найдите гипотенузу треугольника.

  2. В прямоугольном треугольнике катеты равны 8 см и 15 см. Найдите периметр треугольника.

  3. Сторона ромба равна 10 см, а одна из диагоналей – 16 см. Найдите вторую диагональ ромба.

  4. Высота АК равнобедренного треугольника АВС (АВ = ВС) равна 12 см, а КВ = 9 см. Найдите основание треугольника АВС.

  5. Из точки к прямой проведены две наклонные, длины которых равны 13 см и 15 см. Найдите расстояние от точки до прямой, если разность проекций наклонных на эту прямую равна 4 см.

  6. Окружность, вписанная в равнобокую трапецию, делит точкой касания боковую сторону на отрезки длиной 2 см и 32 см. Найдите высоту трапеции

Ответы:

Вариант 1: 1. СВ = 15 см;2. Р = 30 см;3. АВ = 10 см;4. ВС = 2√17 см;5. AD = 12 см;6. СН = 20 см.

Вариант 2: 1. АВ = 50 см;2. Р = 40 см;3. BD = 12 см;4. АС = 6√5 см;5. ВН = 12 см;6. ВН = 16 см.



Контрольная работа по теме «Тригонометрические функции острого угла прямоугольного треугольника. Решение прямоугольных треугольников»

Вариант 1.

  1. В треугольнике АВС известно, что ∠С= 90°, АС= 25 см, ВС= 20 см. Найдите: cos B; 2) tg A.

  2. В прямоугольном треугольнике АВС (∠С= 90°) известно, что АB= 15 см, sin A = 0,6. Найдите катет ВС.

  1. Найдите значение выражения sin2 16° + cos2 16°- sin2 16°.

  2. Основание равнобедренного треугольника равно 12 см, а высота, проведённая к основанию 8 см. Найдите синус, косинус, тангенс и котангенс угла при основании треугольника.

  3. Высота ВD треугольника АВС делит сторону АС на отрезки АD и СD, ВС = 6 см, ∠А = 30°, ∠СВD = 45°. Найдите отрезок AD.

  4. Диагональ равнобокой трапеции перпендикулярна боковой стороне и образует с основанием трапеции угол α. Найдите высоту трапеции, если радиус окружности, описанной около трапеции равен R

Вариант 2.

  1. В треугольнике АВС известно, что ∠С= 90°, АС= 8 см, ВС= 6 см. Найдите: ctg B; 2) sin A.

  2. В прямоугольном треугольнике АВС (∠С= 90°) известно, что АС= 12 см, tg A = 0,8. Найдите катет ВС.

  1. Найдите значение выражения cos2 30°+sin2 52° + cos2 52°.

  2. Основание равнобедренного треугольника равно 10 см, а боковая сторона 13 см. Найдите синус, косинус, тангенс и котангенс угла между боковой стороной треугольника и высотой, проведенной к его основанию.

  3. Высота ВD треугольника АВС делит сторону АС на отрезки АD и СD, АВ = 6 см, ∠А = 60°, ∠СВD = 30°. Найдите отрезок СD.

  4. Диагональ равнобокой трапеции перпендикулярна боковой стороне, а угол между боковой стороной и большим основанием трапеции равен α. Найдите радиус окружности, описанной около трапеции, если её высота равна h.

Ответы:

Вариант 1:1. cos B = 4/5; tg A = 4/3;2. ВС = 9 см;3. ВС = 0,25;4. sin A = 0,8; cos A = 0,6; tg A = 4/3; ctg A = 0,75;5. AD = 3√6 см;6. ВН = R • sin2 α.

Вариант 2:1. ctg B = 0,75; sin A = 0,6;2. BC = 9,6 см;3. 1,25;4. sin В = 5/13; cos В = 12/13; tg В = 5/12; ctg В = 12/5;5. CD = 6 см;6. R = h/(2 sin α • cos α).


Контрольная работа по теме «Многоугольники. Площадь многоугольника»

Вариант 1.

1. Чему равна сумма углов выпуклого четырнадцатиугольника?

2. Площадь параллелограмма равна 84 см2, а одна из его сторон — 12 см. Найдите высоту параллелограмма, проведённую к этой стороне.

3. Боковая сторона равнобедренного треугольника равна 15 см, а высота, проведённая к основанию, — 9 см. Найдите площадь треугольника.

4. Найдите площадь ромба, сторона которого равна 26 см, а одна из диагоналей на 28 см больше другой.

5. Боковая сторона равнобокой трапеции равна 10√2 см и образует с основанием угол 45°. Найдите площадь трапеции, если в неё можно вписать окружность.

6. Биссектриса прямого угла прямоугольного треугольника делит гипотенузу на отрезки длиной 15 см и 20 см. Найдите площадь треугольника.

Вариант 2.

1. Чему равна сумма углов выпуклого восемнадцатиугольника?
2. Площадь параллелограмма равна 98 см2, а одна из его высот — 14 см. Найдите сторону параллелограмма, к которой проведена эта высота.
3. Основание равнобедренного треугольника равно 16 см, а боковая сторона — 17 см. Найдите площадь треугольника.
4. Найдите площадь ромба, сторона которого равна 50 см, а разность диагоналей — 20 см.
5. Боковая сторона равнобокой трапеции образует с основанием угол 60°, а высота трапеции равна 6√3 см. Найдите площадь трапеции, если в неё можно вписать окружность.
6. Биссектриса острого угла прямоугольного треугольника делит катет на отрезки длиной 6 см и 10 см. Найдите площадь треугольника.

Ответы:

Вариант 1:1. S14 = 2160°;2. BH = 7 см;3. S = 108 см2;4. S = 480 см2;5. S = 100√2 см2;6. S = 294 см2.

Вариант 2: 1. S18 = 2880°;2. AD = 7 см;3. S = 120 см2;4. S = 2400 см2;5. S = 72√3 см2;6. S = 96 см2.


Контрольная работа по теме «Итоговая контрольная работа»

Вариант 1.

  1. Найдите углы параллелограмма, если один из них на 26° больше другого.

  2. Продолжения боковых сторон АВ и СD трапеции АВСD пересекаются в точке M. Меньшее основание ВС равно 5 см, ВМ = 6 см, АВ = 12 см. Найдите большее основание трапеции.

  3. Высота АМ треугольника АВС делит его сторону ВC на отрезки ВМ и МС. Найдите сторону АС, если АВ = 10√2 см, МС = 24 см, ∠В = 45°.

  4. Основания равнобокой трапеции равны 12 см и 20 см, а диагональ является биссектрисой её тупого угла. Найдите площадь трапеции.

  5. Перпендикуляр, опущенный из точки окружности на её диаметр, делит его на два отрезка, один из которых на 27 см больше другого. Найдите радиус окружности, если длина данного перпендикуляра равна 18 см.

Вариант 2.

1.Найдите углы параллелограмма, если один из них на 32° меньше другого.

2.Продолжения боковых сторон АВ и СD трапеции АВСD пересекаются в точке Е. Большее основание АD равно 12 см, DЕ = 16 см, СD = 102 см. Найдите меньшее основание трапеции.

3.Высота DЕ треугольника СDF делит его сторону CF на отрезки CE и EF. Найдите сторону СD, если EF = 8 см, DF = 17 см, ∠C = 60°.

4.Основания равнобокой трапеции равны 12 см и 18 см, а диагональ является биссектрисой её острого угла. Найдите площадь трапеции.

5.Перпендикуляр, опущенный из точки окружности на её диаметр, делит его на два отрезка, разность которых равна 21 см. Найдите радиус окружности, если длина данного перпендикуляра равна 10 см.

Ответы:

Вариант 1: № 1. ∠A = 103°; ∠B = 77°; ∠C = 103°; ∠D = 77°;2. AD = 15 см;3. АС = 26 см;4. S = 128√6 см2;5. АО = 22,5 см.

Вариант 2: 1. ∠A = 74°; ∠B = 106°; ∠C = 74°; ∠D = 106°;2. ВС = 4,5 см;3. CD = 10√3 см;4. S = 45√15 см2;5. r = 14,5 см.

Геометрия 7 класс

Алгебра 9 класс ФГОС

Электронная тетрадь по алгебре 8 класс...

Электронная тетрадь по алгебре 11 класс...

Электронная тетрадь по геометрии 9...

Алгебра 8 класс ФГОС

Математика 6 класс ФГОС

Алгебра 7 класс
Скачать

© 2024, 85 0

Рекомендуем курсы ПК и ППК для учителей

Активизация основных видов деятельности учащихся на уроках математики...
800 руб.  4000 руб.
Система работы с высокомотивированными и одаренными учащимися по...
800 руб.  4000 руб.
Развитие пространственных представлений школьников в обучении...
600 руб.  3000 руб.
Современные педагогические технологии в образовательном процессе
800 руб.  4000 руб.
Учитель, преподаватель математики и информатики
3560 руб.  17800 руб.
Методика преподавания математики в соответствии с ФГОС ООО (СОО)
800 руб.  4000 руб.
0 Нет комментариев

Вебинар для учителей

Свидетельство об участии БЕСПЛАТНО!

Полезное для учителя

Новости проекта
03.06.24

Лайфхак учителя №1! Что делать с плохой накопляемостью отметок

12.05.24

Лайфхак учителя №2! Как перестать бегать от ученика к ученику во время практической работы

04.05.24

Лайфхак учителя №3! Что делать, если вы устали из урока в урок повторять одно и то же

Курсы для учителей!
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
Использование табличного процессора в обучении математике
600 руб.
3000 руб.
Учитель, преподаватель математики
2760 руб.
13800 руб.
Исследовательская деятельность учащихся
800 руб.
4000 руб.
Смотреть все курсы


Закрыть через 5 секунд
Комплекты для работы учителя
Поделитесь с друзьями
ВКонтактеОдноклассникиTwitterМой МирLiveJournalGoogle PlusЯндекс