| Дата: | Предмет: алгебра | Учитель: Колодий О.В. |
| Класс: 8 | Раздел: Квадратные уравнения | № урока: 41 |
| Тема: Теорема, обратная теореме Виета |
| Цели урока | Формировать умения применять теорему Виета к решению квадратных уравнений, раскрыть преимущества данной теоремы для приведенного квадратного уравнения. Содействовать развитию математической речи, навыкам быстрого устного счета. Создать условия, обеспечивающие формирование у учеников умений работать в группе. |
| Ожид. результ. | Знают теорему Виета, обратную теорему, находят сумму и произведение корней приведенного квадратного уравнения, находят подбором корни уравнения, проверять корни по теореме Виета |
| Первоначальные знания | Квадратные корни. Квадратное уравнение и его виды. Формула корней. Дискриминант. Приведенные квадратные уравнения. Теорема Виета. |
| Ресурсы | Учебник, раздаточный материал. |
| Ход урока |
| Этап урока | t | Деятельность учителя | Деят-ть учащихся |
| 1.Организационный момент (психологический настрой на урок) | 5 | Психологический настрой: На доске вывешены слова Аристотеля «Познание начинается с удивления». - Ребята, как вы понимаете эти слова? (Да, если мы чему-то удивились, то сразу задаём себе вопросы: «Как?, Почему?» т.е. начинаем думать, анализировать, а значит познавать.) - Мне очень хочется, хотя бы чуть-чуть удивить вас на уроке, чтобы активизировать процесс вашего познания. Обращаю ваше внимание на слова ещё одного великого человека Клода Адриана Гельвеция: «Чтобы удивиться достаточно одной минуты. Чтобы сделать удивительную вещь, нужны многие годы». У нас нет много времени, мы ограничены рамками урока, потому я постараюсь дать направление вашей деятельности на пути к открытию. Деление на группы: произвольное (по рядам) | Настраиваются на урок, делятся на группы, отвечают на вопросы. |
| 2.Вызов | 5 | Анализ проверочной работы: проверка выполнения работы над ошибками. Выводы учащихся по результатам работы. | Выявление проблемных вопросов |
| 3.Осмысление
| 6 | Устный счет №1: проверка теоретических знаний На доске записаны квадратные уравнения: 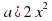 +6х+8=0; ( +6х+8=0; (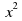 +3х+4=0). Ответ: корней нет. +3х+4=0). Ответ: корней нет.
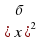 - 7х+10=0; От. 2; 5. - 7х+10=0; От. 2; 5.
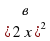 +4х=0; ( +4х=0; (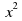 +2х=0). Ответ: -2; 0. +2х=0). Ответ: -2; 0.
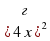 - 100 =0; ( - 100 =0; (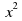 - - 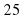 =0). Ответ: -5;5. =0). Ответ: -5;5.
Вопросы к классу: 1.Что написано на доске? (Квадратные уравнения). 2.Докажите, что данные уравнения квадратные. (Уравнения имеют вид ах2 + bx + c = 0, а 0). 3.Какие виды квадратных уравнений в зависимости от количества слагаемых вы знаете? (Полные и неполные). 4.Назовите полные квадратные уравнения. Почему они так называются? 5.Назовите неполные квадратные уравнения. Почему они так называются? 6.По какому ещё признаку квадратные уравнения делятся на две группы? (Если старший коэффициент равен 1, то это приведённое квадратное уравнение, если а 1, то это неприведённое квадратное уравнение). 7.Назовите приведённые и неприведённые уравнения. Можно ли из неприведённого квадратного уравнения получить приведённое? | Отвечают на вопросы, анализируют, доказывают. Оценивание устных ответов в группе. |
| 4 | Устный счет №2: проверка практических знаний 1.Найдите сумму и произведение корней уравнения: х² - 37х + 27 = 0; у² + 41у – 371 = 0; у² - 19 = 0; -х² + х = 0. 2.Не решая уравнения, определить знаки его корней: х² + 4х – 5 = 0; х² - 5х + 3 = 0; х² - 8х – 7 = 0. 3.Один из корней уравнения х² - 19х + 18 = 0 равен 1. найти его второй корень. | Участвуют в решении заданий. Оценивание устных ответов в группе. |
| 6 | Обучающая самостоятельная работа с самопроверкой 1. Проверьте, правильно ли найдены корни квадратного уравнения: а) х2 + 3х – 40 = 0, х1 = –8, х2 = 5; б) х2 + 2х – 3 = 0, х1 = –1, х2 = 3. 2. Определить знаки корней квадратного уравнения: а) х2 – х – 12 = 0; б) х2 – 7х + 12 = 0. 3. Определите корни квадратного уравнения, не используя формулу корней: а) х2 - 6х + 5 = 0; б) х2 + 9х + 20 = 0. 4. Составьте приведенные квадратные уравнения, если его корни равны: а) х1 = –3, х2 = 1; б) х1 = 5, х2 = 6. Ответы:1.а) да, б) нет; 2.а)+,-;б) +,+; 3.а)1;5; б)-5; -4; 4 а) а) х2 +2х - 3 = 0; б) х2 – 11х + 30 = 0. | Решают, комментируют, самопроверка правильности решения |
| 11 | Повторение темы «Квадратные уравнения» (решение через дискриминант) 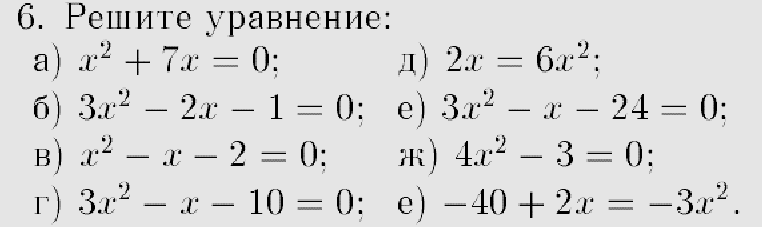
| Выполняют в группах решение уравнений. Оценивание работы группой
|
| 4. Домашнее задание | 3 | № 297(4,5,9), стр 66 изучить теорему 3 и выполнить №296(1,2)еня сегодня хорошо получалось...не все способы решения квадратных уравнений нами рассмотрены | Слушают, делают карандашом пометки. |
| 5. Рефлексия | 5 | Синквейн: – это пятистрочная строфа. 1-я строка – одно ключевое слово, определяющее содержание синквейна; 2-я строка – два прилагательных, характеризующих данное понятие; 3-я строка – три глагола, обозначающих действие в рамках заданной темы; 4-я строка – короткое предложение, раскрывающее суть темы или отношение к ней; 5-я строка – синоним ключевого слова (существительное). | Составляют синквейн |






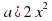 +6х+8=0; (
+6х+8=0; (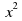 +3х+4=0). Ответ: корней нет.
+3х+4=0). Ответ: корней нет.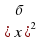 - 7х+10=0; От. 2; 5.
- 7х+10=0; От. 2; 5.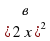 +4х=0; (
+4х=0; (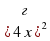 - 100 =0; (
- 100 =0; (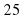 =0). Ответ: -5;5.
=0). Ответ: -5;5.