Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Ульяновский государственный педагогический
университет имени И.Н. Ульянова»
(ФГБОУ ВО «УлГПУ им. И.Н. Ульянова»)
Кафедра методик математического и информационно-технологического образования
КУРСОВАЯ РАБОТА
Решение тригонометрических уравнений и неравенств с параметрами.
студентки 3 курса группы МИЯ-15
Специальность / Направление подготовки 44.03.05 Педагогическое образование
Специализация / Профиль Математика/ Иностранный язык
Заключновой Ирины Сергеевны
Научный руководитель к.п.н., доцент Кузина Н.Г.
_____________________ _____________/_______________
(оценка цифрой и прописью) (подпись науч. рук-ля / расшифровка подписи)
_________________________ _______________
(количество баллов) (дата)
___________ №__________
(дата) (журнал регистрации)
______________________
(должность регистрирующего)
__________/____________
(подпись / расшифровка)
Ульяновск 2018
Оглавление
Введение 2
Глава 1. Теоретические основы решения тригонометрических уравнений и неравенств с параметром 4
1.1 Исторические сведения о развитии тригонометрии 4
1.2 Тождественные преобразования тригонометрических выражений 5
1.3 Параметр 9
1.4 Методы решения тригонометрических уравнений с параметром 10
1.4 Решение тригонометрических неравенств с параметром 16
Выводы по первой главе 21
Глава 2. Практикум по решению тригонометрических уравнений и неравенств с параметром 22
2.1 Решение тригонометрических уравнений с параметром 22
2.2 Решение тригонометрических неравенств с параметром 28
Выводы по второй главе 33
Заключение 34
Список используемых источников 36
Введение
Данная работа посвящена исследованиям, лежащим в области математики, и касается тригонометрического раздела математики. Актуальность данной темы состоит в том, что тригонометрические уравнения одна из самых сложных тем в школьном курсе. Тригонометрические уравнения возникают при решении задач по планиметрии, стереометрии, астрономии, физики и в других областях. Тригонометрические уравнения и неравенства из года в год встречаются среди заданий ЕГЭ для 11 класса. А тригонометрические уравнения и неравенства с параметрами – наиболее сложные, но зато и самые интересные. Именно задачи такого типа развивают сообразительность, смекалку, догадливость, находчивость в учениках. Самое важное отличие тригонометрических уравнений от алгебраических состоит в том, что в алгебраических уравнениях имеют конечное число корней, а в тригонометрических - бесконечное, что сильно усложняет отбор корней и выбор значения параметра.
Цель курсовой работы заключается в овладении методами решения основных типов тригонометрических уравнений и неравенств с параметрами.
Для осуществления обозначенной цели служат следующие задачи:
-
Отобрать теоретические сведения необходимые для решения тригонометрических уравнений и неравенств с параметрами
-
Сформировать понимание у учащихся работы с тригонометрическими задачами с параметрами
-
Выделить основные типы тригонометрических уравнений с параметрами и методы их решения на основе рассмотрения примеров
-
Овладеть методами решения основных типов тригонометрических уравнений и неравенств с параметрами
-
Изучить различные подходы и методы решений тригонометрических уравнений и неравенств с параметрами
Объект исследования – тригонометрические уравнения и неравенства с параметром. Предмет исследования – методы решения тригонометрических уравнений и неравенств с параметром.
При написании курсовой работы были использованы методы исследования: теоретические (анализ, классификация, индукция, обобщение) и практические (сравнение, материальное моделирование).
Методологической основой для исследования послужили научные труды известных математиков. В качестве теоретической базы исследования были использованы научные статьи, учебники по математике: Гусятников Н.В., Гусятников В.В.; Коноплева О.А. Практической базой исследования послужили сборники задач: Евдокимова Н.Н.; Мордкович А.Г., Литвиненко В.Н.
Глава 1. Теоретические основы решения тригонометрических уравнений и неравенств с параметром
- Исторические сведения о развитии тригонометрии
Слово «тригонометрия» составлено из двух греческих слов: «тригонон» - треугольник и «метрео» - измеряю. Основной задачей тригонометрии является нахождение неизвестных параметров треугольника по данным значениям других его параметров.
Первые методы нахождения неизвестных параметров данного треугольника были развиты учеными Древней Греции за несколько веков до нашей эры. Греческие астрономы не знали синусов, косинусов и тангенсов. Вместо таблиц этих величин они употребляли таблицы, позволявшие отыскивать хорду окружности по стягиваемой ею дуге. Дуги измерялись в градусах и минутах.
Все древние цивилизации вносили свой клад в дело накопления тригонометрических знаний. На одной из глиняных табличек Древнего Вавилова, возраст которой определяется вторым тысячелетием до нашей эры, решается тригонометрическая задача.
Значительно развили тригонометрию индийские средневековые астрономы и арабские ученые. В X веке багдадский ученый Абу-ль-Вефа присоединил к понятиям синусов и косинусов понятия тангенсов, котангенсов, секансов и косекансов. Абу-ль-Вефа установил также основные соотношения между ними. Благодаря работам знаменитого арабского ученого Насир эд-Дина (1201-1274) тригонометрия становится самостоятельной научной дисциплиной. Насир эд-Дин рассмотрел все случаи решения плоских и сферических треугольников. В XII веке с арабского языка на латинский был переведен ряд астрономических работ, по которым европейцы познакомились с тригонометрией, не многие работы Насир эд-Дина остались им неизвестны.
Выдающийся немецкий астроном XV века Региомонтан (1436-1476) заново сформулировал теоремы Насир эд-Дина. Региомонтан составил таблицы синусов плоских углов с точностью до седьмой значащей цифры. В середине XVIII века, благодаря русскому академику Леонарду Эйлеру (1707-1783), тригонометрия приняла современный вид. Он разработал её как науку о тригонометрических функциях, ввел записи 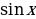 , tg x, обозначил а, в, с для сторон А,В,С для противоположных углов
, tg x, обозначил а, в, с для сторон А,В,С для противоположных углов  .
.
Эйлер рассматривал тригонометрические функции аргумента х – радианной меры соответствующего угла, давая этому аргументу различные значения: положительные, отрицательные и даже комплексные. Он же ввел и обратные тригонометрические функции.
- Тождественные преобразования тригонометрических выражений
Напомним основные факты тригонометрии.
-
Знаки тригонометрических функций по четвертям:
| Четверть | sin x | cos x | tg x | ctg x |
| I | + | + | + | + |
| II | + | - | - | - |
| III | - | - | + | + |
| IV | - | + | - | - |
-
Некоторые значения тригонометрических функций
| x | 0 | 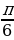
| 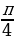
| 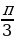
| 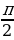
| 
| 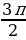
|
| sin x | 0 | 
| 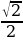
| 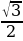
| 1 | 0 | -1 |
| cos x | 1 | 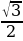
| 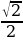
| 
| 0 | -1 | 0 |
| tg x | 0 | 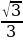
| 1 | 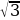
| - | 0 | - |
| ctg x | - | 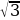
| 1 | 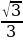
| 0 | - | 0 |
-
Четность, периодичность.
Функция y=cos x является четной, остальные тригонометрические функции нечетные:
sin(-x)=-sin x,
cos(-x)=cos x,
tg(-x)=-tg x ( x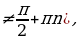
ctg(-x)=-ctg x (x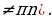
Все тригонометрические функции являются периодическими. При этом Т=2 – основной период функций y=sin x, y=cos x, а Т=
– основной период функций y=sin x, y=cos x, а Т= – основной период функции y=tg x, y=ctg x. Напомним, что основным периодом называется наименьший период из множества всех положительных периодов периодической функции. Таким образом,
– основной период функции y=tg x, y=ctg x. Напомним, что основным периодом называется наименьший период из множества всех положительных периодов периодической функции. Таким образом,
sin(x+2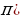 =sin(x-2
=sin(x-2 )=sin x,
)=sin x,
cos(x+2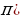 =cos(x-2
=cos(x-2 )=cos x,
)=cos x,
tg(x+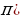 =tg(x-
=tg(x- )=tg x ( x
)=tg x ( x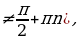
ctg(x+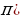 =ctg(x-
=ctg(x- )=ctg x (x
)=ctg x (x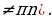
-
Формулы сложения аргументов:
sin(x y)=sin x cos y
y)=sin x cos y  sin y cos x,
sin y cos x,
cos(x y)=cos x cos y
y)=cos x cos y 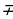 sin x sin y,
sin x sin y,
tg(x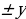 )=
)=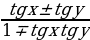 ( x
( x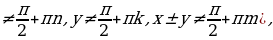
ctg(x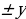 )=
)=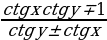 ( x
( x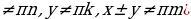 .
.
-
Формулы, связывающие тригонометрические функции одного и того же аргумента:
cos2 x + sin2 x =1,
tg x = 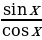 ( x
( x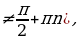
ctg x = 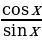 ( x
( x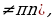
1+ tg2 x = 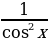 ( x
( x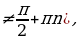
1+ ctg2 x = 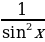 ( x
( x .
.
-
Формулы, связывающие тригонометрические функции аргументов, из которых один вдвое больше другого:
sin 2x = 2 sin x cos x,
cos 2x = cos2 x – sin2 x,
tg 2x = 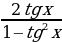 (x
(x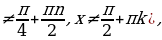
ctg 2x = 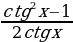 (x
(x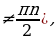
1 + cos 2x = 2 cos2 x,
1 - cos 2x = 2 sin2 x,
1 sin 2x = (cos x
sin 2x = (cos x  sin x)2.
sin x)2.
-
Формулы приведения:
| x | 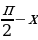
| 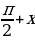
| 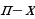
| 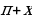
| 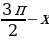
| 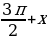
| 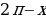
|
| sin x | cos x | cos x | sin x | - sin x | - cos x | - cos x | - sin x |
| cos x | sin x | - sin x | - cos x | - cos x | - sin x | sin x | cos x |
| tg x | ctg x | - ctg x | - tg x | tg x | ctg x | - ctg x | - tg x |
| ctg x | tg x | - tg x | - ctg x | ctg x | tg x | - tg x | - ctg x |
Для облегчения запоминания указанных в таблице формул приведения можно применять следующее мнемоническое правило:
1) если дуга х откладывается от горизонтального диаметра (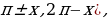 то название функции сохраняется; если дуга х откладывается от вертикального диаметра (
то название функции сохраняется; если дуга х откладывается от вертикального диаметра ( 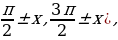 то название функции меняется ( синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс);
то название функции меняется ( синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс);
2) перед полученной функцией ставят тот знак, который имела бы выводимая функция в случае, если 0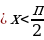 .
.
-
Формулы преобразования суммы тригонометрических функций в произведение:
sin x + sin y = 2 sin 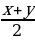 cos
cos 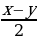 ,
,
sin x - sin y = 2 sin 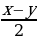 cos
cos 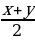 ,
,
cos x + cos y = 2 cos 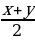 cos
cos 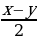 ,
,
cos x - cos y = 2 sin 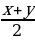 sin
sin 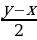 ,
,
tg x  tg y =
tg y = 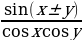 (x
(x
ctg x  ctg y =
ctg y = 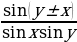 (x
(x
-
Формулы преобразования произведения тригонометрических функций в сумму:
sin x cos y = 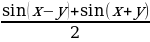 ,
,
cos x cos y = 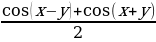 ,
,
sin x sin y = 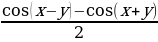 .
.
- Параметр
Имеется несколько определений параметра:
Параметр – это величина, входящая в формулы и выражения, значение которой является постоянным в пределах рассматриваемой задачи, но в другой задаче меняет свои значения.
Переменные a, b, c, …, k, которые при решении уравнения или неравенства считаются постоянными, называются параметрами, а само уравнение (неравенство) называется уравнением (неравенством), содержащим параметры.
Для решения квадратных уравнений с параметром необходимо находить контрольные значения параметра. Контрольные значения параметра – те значения, при которых обращается в 0:
- старший коэффициент в уравнении или в неравенстве;
- знаменатели в дроби;
- дискриминант квадратного двучлена.
1.4 Методы решения тригонометрических уравнений с параметром
Решить уравнение f (х; а) = 0 с параметром а – это значит, для каждого действительного значения а найти значения х, удовлетворяющих уравнению, или установить, что таких нет.
При решении тригонометрических уравнений с параметром наряду с единичной окружностью можно пользоваться координатной прямой для параметра. По мере решения уравнения на прямой появляются точки, разбивающие прямую на части, над каждой из которых записываем множество корней уравнения. Если координатная прямая заполнена, то это свидетельствует о том, что решение закончено и можно записывать ответ. При решении уравнений с параметрами нам будут необходимы знания о решении тригонометрических уравнения без параметра, поэтому рассмотрим далее методы их решения.
Напомним общие формулы решений простейших тригонометрических уравнений (если не сделано оговорок, то предполагается, что параметры n, k, l, m, … принимают любые целые значения).
| Уравнение | Решение |
| sin x = a, где 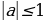 | x = (-1)k arcsin a + 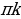 |
| сos x = a, где 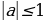 | x = 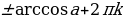 |
| tg x = a | x = 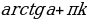 |
| ctg x = a | x = 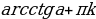 |
Отметим особо некоторые частные случаи простейших тригонометрических уравнений, когда решение может быть записано без применения общих формул:
sin x = 0  x =
x = 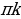 ,
,
sin x = 1  x =
x = 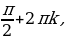
sin x = -1  x =
x = 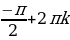 ,
,
cos x = 0  x =
x = 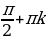 ,
,
cos x = 1  x =
x = 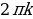 ,
,
cos x = -1  x =
x = 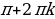 .
.
Проверка найденных решений необходима:
-
Если в процессе решения произошло расширение области определения уравнения в результате некоторых преобразований (освобождение от знаменателей, сокращение дроби, приведение подобных членов),
-
Если в процессе решения уравнения использовалось возведение обеих частей уравнения в одну и ту же четную степень,
-
Если при решении применялись тригонометрические тождества, левая и правая части которых имеют неодинаковые области определения.
Основными методами, используемыми при решении тригонометрических уравнений, являются следующие методы: разложение на множители, сведение к квадратным уравнениям, решение однородных уравнений, универсальная подстановка, с помощью замены неизвестного, применение формул понижения степени, с применением формул тройного аргумента.
-
Решение тригонометрических уравнений разложением на множители. Метод разложения на множители заключается в следующем: если f(x)=f1(x) f2(x) … fn(x), то всякое решение уравнения f(x)=0 является решением совокупности уравнений f1(x)=0, f2(x)=0, … , fn(x)=0.
Обратное утверждение, неверно: не всякое решение совокупности уравнений является решением уравнения. Это объясняется тем, что решения отдельных уравнений могут не входить в область определения функции f(x). Поэтому, если при решении тригонометрического уравнения методом разложения на множители, функции, входящие в уравнение, определены не для всех значений аргумента, после нахождения решения должна быть сделана проверка, чтобы исключить лишние корни. можно поступать другим способом: находить область допустимых значений исходного уравнения и выбирать только те корни, которые входят в найденную область допустимых значений.
Пример №1. Решите уравнение: (2sin x – cos x)(1+ cos x)=sin2 x
(2sin x – cos x)(1+ cos x)=1 – cos2 x;
(2sin x – cos x)(1+ cos x)= (1- cos x) (1+ cos x);
(2sin x – cos x)(1+ cos x)- (1- cos x) (1+ cos x) ;
(1+ cos x)( 2sin x – cos x-1+ cos x)=0 
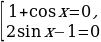

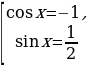
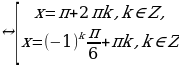
Ответ: 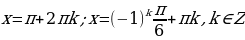
-
Решение тригонометрических уравнений, сводящихся к квадратным. При решении уравнений указанного типа в основном применяются следующие тригонометрические тождества:
sin2 x + cos2 x=1,
tg2 x + 1=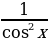 , x
, x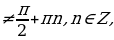
ctg2 x + 1=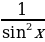 , x
, x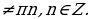
Пример №2. Решите уравнение: 6cos2 x +5sinx – 7 = 0
6(1-sin2 x) +5sinx – 7 = 0;
6sin2 x -5sinx +1 = 0;
Введем подстановку y=sin x, тогда получаем квадратное уравнение
6y2 – 5y +1 = 0. Находим корн у1 =  , у2 =
, у2 = 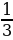 . Затем осуществляем обратную подстановку sin x =
. Затем осуществляем обратную подстановку sin x = , sin x =
, sin x =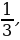 получаем решение исходного уравнения.
получаем решение исходного уравнения.
Ответ: x = 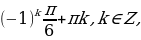 x =
x = 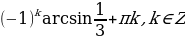
-
Решение однородных уравнений. Уравнение вида
b0sinn ax + b1sinn-1 ax cos ax + b2sinn-2 ax cos2 ax + … +
+ b0n-1 sin ax cosn-1 ax + bncosn ax = 0, где b0, b1, … , bn - действительные числа, называются однородными уравнениями степени n относительно функций sin ax, cos ax. Общий подход к решению однородных уравнений основан на том, что корни уравнений sin ax = 0 или cos ax = 0 не являются корнями уравнения, так как, если, например cos ax = 0, то из уравнения следует, что и sin ax = 0, что противоречит основному тригонометрическому тождеству cos2 x + sin2 x =1. Следовательно, левую и правую части уравнения можно разделить на cosn ax и ввести подстановку y=tg ax, или разделить на sinn ax и ввести подстановку y=ctg ax.
Пример №3. Решите уравнение: sin x – 2cos x = 0
Уравнение является однородным уравнением первой степени. Разделим на cos x, получаем равносильное уравнение tg x = 2.
Ответ: x=arctg2 +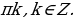
-
Решение уравнений с помощью введения вспомогательного аргумента. Рассмотрим уравнение asin x + bcos x = c, a2+b2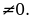 Разделим левую и правую части уравнения на
Разделим левую и правую части уравнения на 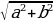 :
:
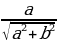 sin x +
sin x +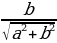 cos x =
cos x = 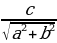 . Так как
. Так как 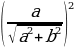 +
+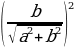 =1, то существует угол
=1, то существует угол 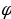 такой, что cos
такой, что cos 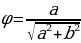 , sin
, sin 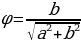 , при этом
, при этом 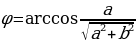 (или
(или 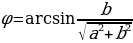 ). Тогда уравнение примет вид sin x cos
). Тогда уравнение примет вид sin x cos 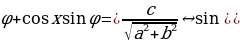 +
+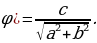
Пример №4. Решите уравнение: sin x + cos x = 1
Разделим левую и правую часть уравнения на 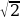 . Тогда получим
. Тогда получим
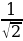 sin x +
sin x + 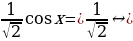 cos
cos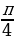 sin x + sin
sin x + sin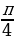 cos x =
cos x = 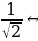
 sin (x +
sin (x +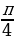 ) =
) =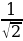
 x= -
x= - 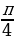 +
+ 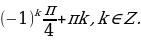
Ответ: x= - 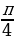 +
+ 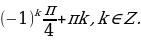
-
Решение уравнений методом универсальной подстановки. Тригонометрическое уравнение вида R (sin kx, cos nx, tg mx, ctg lx)=0, где R – рациональная функция, k, l, m, n 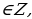 с помощью тригонометрических формул двойного и тройного аргумента, а также формул сложения можно свести двойного и тройного аргумента, а также формул сложения можно свести к рациональному уравнению относительно аргументов sin x, cos x, tg x, ctg x, после чего уравнение может быть сведено к рациональному уравнению относительно t = tg
с помощью тригонометрических формул двойного и тройного аргумента, а также формул сложения можно свести двойного и тройного аргумента, а также формул сложения можно свести к рациональному уравнению относительно аргументов sin x, cos x, tg x, ctg x, после чего уравнение может быть сведено к рациональному уравнению относительно t = tg 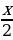 с помощью формул универсальной тригонометрической подстановки
с помощью формул универсальной тригонометрической подстановки
sin x = 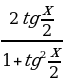 , cos x =
, cos x = 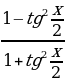 ,
,
tg x = 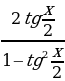 , ctg x =
, ctg x = 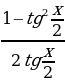 .
.
Следует отметить, что применение формул может приводить к сужению ОДЗ исходного уравнения, поскольку tg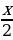 не определен в точках, необходимо делать проверку корней.
не определен в точках, необходимо делать проверку корней.
Пример №5. Решите уравнение:sin x + tg 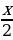 = 0
= 0
По условию задачи х 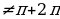 k, k
k, k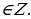 Применив формулы и сделав замену t = tg
Применив формулы и сделав замену t = tg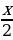 , получим
, получим 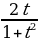 + t = 0, откуда t=0 и, следовательно, x =2
+ t = 0, откуда t=0 и, следовательно, x =2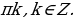
Ответ: x =2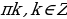 .
.
-
Решение тригонометрических уравнений с помощью замены неизвестного. Уравнение вида P (sin x cos x;sin x cos x) = 0 решается следующей заменой sin x
cos x;sin x cos x) = 0 решается следующей заменой sin x  cos x = y, (sin x
cos x = y, (sin x  cos x)2 = y2, 1
cos x)2 = y2, 1 2 sin x cos x = = y2,
2 sin x cos x = = y2,  2 sin x cos x = y2-1.
2 sin x cos x = y2-1.
Пример №6. Решите уравнение: 2(sin x + cos x) + sin 2x +1 = 0, x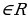
2(sin x + cos x) + 2 sin x cos x +1 = 0;
Пусть sin x + cos x = y, (sin x + cos x)2 = y2, 1+ 2 sin x cos x = y2,
2 sin x cos x = y2 -1, получим y2+2y-1+1 =0 ; y2 + 2y=0; y(y+2)=0
-
y=0: sin x + cos x = 0, разделим на cos x 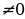 , получим tg x = -1,
, получим tg x = -1,
x = - 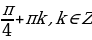
-
y= - 2: sin x + cos x = - 2, 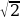 sin (x +
sin (x +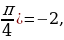 sin (x +
sin (x +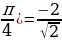 , т.к.
, т.к. 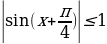 , при х
, при х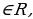 то корней нет
то корней нет
Ответ: x = - 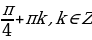
-
Решение уравнения с применением формул понижения степен. При решении широкого круга тригонометрических уравнений ключевую роль играют формулы понижения степени:
sin2 x =  (1-cos 2x),
(1-cos 2x),
cos2 x =  (1+cos 2x).
(1+cos 2x).
Пример №7. Решите уравнение: sin2 x + sin2 2x – sin2 3x – sin2 4x = 0. Применив формулу понижения степени, получим
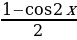 +
+ 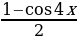 -
- 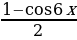 -
- 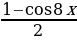 = 0,
= 0,

-2 sin 3x sin 5x -2 sin x sin 5x = 0,
2 sin 5x (sin 3x + sinx) = 0, 4sin 5x sin 2x sin x = 0. Последнее уравнение равносильно совокупности трех уравнений:
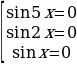
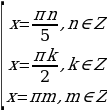
Решение из множества 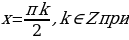 k=2l, l
k=2l, l 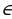 Z содержаться в множестве
Z содержаться в множестве 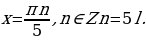
Ответ: 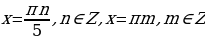
-
Решение уравнений с применением формул тройного аргумента. При решении ряда уравнений наряду с другими существенную роль играют формулы
sin 3x = 3sin x – 4sin3 x,
cos 3x = 4 cos3 x – 3cos x.
Пример №8. Решите уравнение: cos 3x = - 2cos x
Применив формулу, получим cos x ( 4cos2 x – 1) = 0 
cos x ( cos 2x + 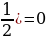 . Последнее уравнение равносильно совокупности двух уравнений:
. Последнее уравнение равносильно совокупности двух уравнений:
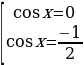
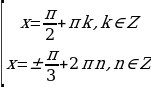
Ответ: 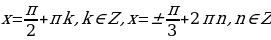
- Решение тригонометрических неравенств с параметром
Решение тригонометрических неравенств сводится, как правило, к решению простейших тригонометрических неравенств, т.е. неравенств вида sinx a, cos x a и т.д., также к решению совокупностей, систем или совокупностей систем простейших тригонометрических неравенств.
Для решения простейших тригонометрических неравенство для решения простейших тригонометрических неравенств во многих случаях удобно пользоваться геометрическим методом или с помощью окружности, на которой множество значений переменной, удовлетворяющих заданному простейшему неравенству, изображается в виде одной или нескольких дуг.
Аналогично тому, как с помощью неравенств задаются промежутки на числовой прямой, можно записывать и множество точек, принадлежащих той или иной дуге окружности  Условимся символом
Условимся символом  М1М2 обозначать дугу, для которой точка М1 – начальная точка (в обозначении дуги она записывается первой), М2 - конечная точка пути, описываемого текущей точкой по окружности
М1М2 обозначать дугу, для которой точка М1 – начальная точка (в обозначении дуги она записывается первой), М2 - конечная точка пути, описываемого текущей точкой по окружности 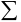 в положительном направлении (против часовой стрелки).
в положительном направлении (против часовой стрелки).
Разберем случаи простейших уравнений для некоторых тригонометрических функций.
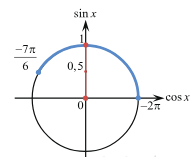
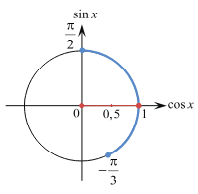
Пример №9. Решите неравенство: 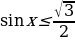
Первый способ: Решим это неравенство графически. Для этого построим в одной системе координат график синуса y=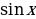 и прямой y=
и прямой y=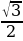 (рис. 1)
(рис. 1)
Выделим промежутки, на которых синусоида расположена ниже графика прямой y=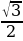 . Найдем абсциссы х1 и х2 точек пересечения этих графиков:
. Найдем абсциссы х1 и х2 точек пересечения этих графиков:
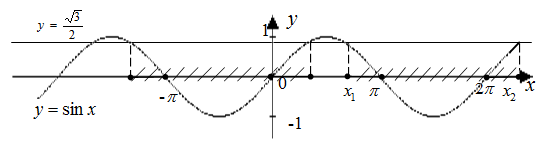
(рис. 1)
х1 = 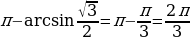
х2 = 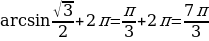
Получили интервал 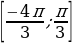 , но так как функцию y=sin x периодическая и имеет период 2
, но так как функцию y=sin x периодическая и имеет период 2 , то ответом будет объединение интервалов:
, то ответом будет объединение интервалов: 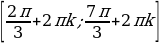 , k
, k
Второй способ: Построим единичную окружность и прямую y=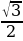 , точки их пересечения обозначим Px1 и Px2 (рис. 2). Решением исходного неравенства будет множество точек ординаты, которых меньше
, точки их пересечения обозначим Px1 и Px2 (рис. 2). Решением исходного неравенства будет множество точек ординаты, которых меньше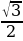 . Найдем значение х1 и х2, совершая обход против часовой стрелки, х12:
. Найдем значение х1 и х2, совершая обход против часовой стрелки, х12:
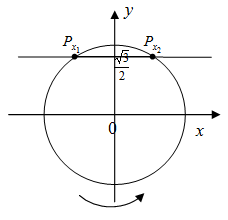
(рис. 2)
х1 = 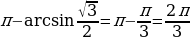
х2 = 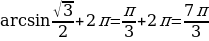
Учитывая периодичность функции синус, окончательно получим интервалы 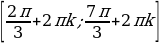 , k
, k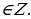
Ответ: х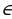
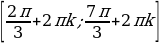 , k
, k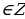
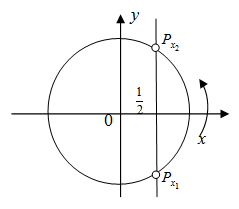
Пример №10. Решите неравенство: cos x 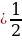
Построим единичную окружность и прямую x= (так как на единичной окружности косинусам отвечает ось абсцисс). Обозначим Px1 и Px2 (рис. 3) – точки пересечения прямой и единичной окружности. Решением исходного уравнения будет множество точек абсциссы, которых меньше
(так как на единичной окружности косинусам отвечает ось абсцисс). Обозначим Px1 и Px2 (рис. 3) – точки пересечения прямой и единичной окружности. Решением исходного уравнения будет множество точек абсциссы, которых меньше  . Найдем значение x1 и x2, совершая обход против часовой стрелки так, чтобы x12:
. Найдем значение x1 и x2, совершая обход против часовой стрелки так, чтобы x12:
(рис. 3)
x1=-arccos = -
= - 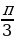 ; x2=arccos
; x2=arccos =
= 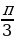
Учитывая периодичность косинуса, окончательно получим интервалы 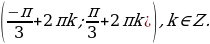
Ответ: х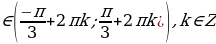
Пример №11. Решите неравенство: ctg x 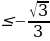
Построим в одной системе координат графики функций: y=ctg x, y=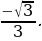 Выделим промежутки, на которых график функции y=ctg x расположен не выше графика прямой y=
Выделим промежутки, на которых график функции y=ctg x расположен не выше графика прямой y=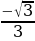 (рис. 4).
(рис. 4).
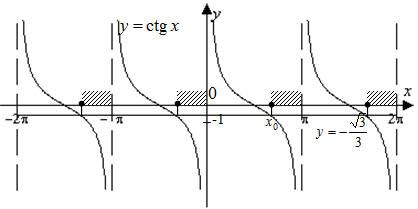
(рис. 4)
Найдем абсциссу точки x0, которая является концом одного из промежутков, на котором неравенство
x0=arcctg(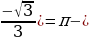 arcctg(
arcctg(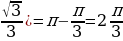
Другим концом этого промежутка есть точка  , а функция y=ctg x в этой точке неопределенна. Таким образом, одним из решением данного неравенства является промежуток
, а функция y=ctg x в этой точке неопределенна. Таким образом, одним из решением данного неравенства является промежуток 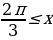
 . Учитывая, что котангенс функция периодическая, с периодом
. Учитывая, что котангенс функция периодическая, с периодом  , то окончательно получим
, то окончательно получим 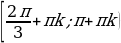 , k
, k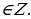
Ответ: х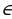
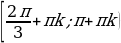 , k
, k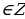
Если неравенство f(x; р) , ,
Решить неравенство с параметром - значит найти все значения параметров, при которых данные для решения тригонометрические неравенства будут иметь решение.
Выводы по первой главе
В первой главе были рассмотрены исторические сведения о развитии тригонометрии, тождественные преобразования тригонометрических выражений, которые необходимо знать для решения уравнений и неравенств. Определено, что такое параметр и его контрольные значения. При решении уравнений с параметрами нам будут необходимы знания о решении тригонометрических уравнения без параметра, поэтому были рассмотрены простейшие тригонометрические уравнения и восемь методов их решения, записаны решения для частных случаев простейших уравнений. Каждый метод был проиллюстрирован примером. Так же были рассмотрены методы решения тригонометрических неравенств, и разобраны случаи простейших уравнений для некоторых тригонометрических функций. Чтобы разобрать оба метода решения неравенств (геометрический и с помощью окружности) один из примеров решен двумя способами.
Глава 2. Практикум по решению тригонометрических уравнений и неравенств с параметром 2.1 Решение тригонометрических уравнений с параметром
Пример№1: Найдите все значения параметра а, при каждом из которых уравнение cos4 x – (a + 2)cox2x – (a + 3) = 0 имеет решение.
Введем новую переменную: t =cos2x, t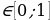 . Тогда данное уравнение принимает вид t2 – (а + 2)t – (a + 3) = 0. Чтобы решить получившееся квадратное уравнение с переменной t, найдем его дискриминант: D = a2 + 4a + 4 + + 4a + 12 = a2 + 8a + 16 = (a + 4)2. Так как D≥0, квадратное уравнение имеет решение:
. Тогда данное уравнение принимает вид t2 – (а + 2)t – (a + 3) = 0. Чтобы решить получившееся квадратное уравнение с переменной t, найдем его дискриминант: D = a2 + 4a + 4 + + 4a + 12 = a2 + 8a + 16 = (a + 4)2. Так как D≥0, квадратное уравнение имеет решение:
t1,2 =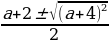 =
= 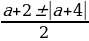 =
= 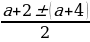
t1 = 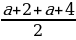 =
= 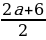 =
= 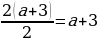
t2 = 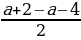 =
= 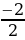 = -1
= -1
Число -1 не принадлежит промежутку 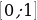 таким образом, заданное нам тригонометрическое уравнение с параметром имеет решение при условии
таким образом, заданное нам тригонометрическое уравнение с параметром имеет решение при условии
0 ≤ а +3 ≤ 1,
-3 ≤ а ≤ -2.
Ответ. Уравнение cos 4 x – (a + 2) cos2x – (a + 3) = 0 имеет решение при
a 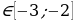 .
.
Пример№2: Найдите все значения параметра р, при которых уравнение
6sin3 x = p – 10cos 2x не имеет корней.
6sin3 x = p – 10cos 2x;
6sin3 x + 10cos 2x = p;
6sin3 x + 10(1 – 2sin2 x) = p;
6sin3 x – 20sin2 x + 10 = p.
Введем новую переменную: t = sin x, t 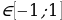 тогда тригонометрическое уравнение примет вид 6t3 – 20t2 + 10 = p. Рассмотрим функцию
тогда тригонометрическое уравнение примет вид 6t3 – 20t2 + 10 = p. Рассмотрим функцию
у = 6t3 – 20t2 + 10 и исследуем ее на наибольшее и наименьшее значения на отрезке 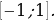 Находим производную: у
Находим производную: у = 18t2 - 40t = 18t (t -
= 18t2 - 40t = 18t (t - 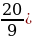 . Определяем критические точки функции: у′=0, 18t(t -
. Определяем критические точки функции: у′=0, 18t(t - 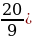 , t1=0, t2 =
, t1=0, t2 =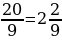 .
.
Число 2 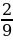 не принадлежит промежутку
не принадлежит промежутку 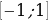 , поэтому вычисляем значения функции в точке 0 и на концах отрезка:
, поэтому вычисляем значения функции в точке 0 и на концах отрезка:
у(0) = 0 – 0 + 10 = 10,
у(-1) = -6 – 20 + 10 = -16,
у(1) = 6 – 20 + 10 = -4.
ymax (t) = 10, ymin (t) = -16 на отрезке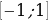 . Значит, при
. Значит, при
p 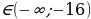
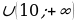 исходное уравнение не имеет корней.
исходное уравнение не имеет корней.
Ответ. Уравнение 6sin3x = p – 10cos2x не имеет корней при
p 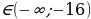
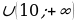
Пример№3: Решите уравнение sin4 x + cos4 x = a
Применяя формулы понижения степени получим:
(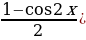 2 + (
2 + (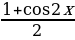 )2 = a, и далее cos2 2x = 2a – a.
)2 = a, и далее cos2 2x = 2a – a.
Найдем контрольные значения параметра. В данном случае это такие значения параметра, при которых правая часть уравнения 0 или 1
(если 2а – 1 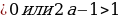 , то уравнение не имеет решений). Если
, то уравнение не имеет решений). Если
2а – 1 =0, то а =  ; если 2а – 1= 1, то а = 1. И так, рассмотрим уравнение
; если 2а – 1= 1, то а = 1. И так, рассмотрим уравнение
cos 4x = 4a -3в каждом из пяти случаев: 1) а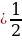 ; 2) а =
; 2) а =  ; 3)
; 3) 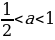 ; 4) а=1; 5) а
; 4) а=1; 5) а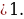
1) Если а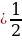 , то 2а – 1
, то 2а – 1  и уравнение cos2 2x = 2a – a не имеет корней
и уравнение cos2 2x = 2a – a не имеет корней
2) Если а = 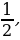 то уравнение cos2 2x = 2a – a принимает вид cos2 2x = 0, откуда находим x =
то уравнение cos2 2x = 2a – a принимает вид cos2 2x = 0, откуда находим x = 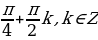
3) Если 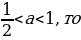 0
0 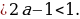 Преобразуем уравнение
Преобразуем уравнение
cos2 2x = 2a – a к виду: 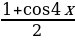 = 2a – 1, и далее cos 4x = 4a -3. Так как в рассматриваемом случае
= 2a – 1, и далее cos 4x = 4a -3. Так как в рассматриваемом случае 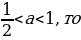 2
2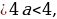 а тогда
а тогда 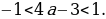 Значит, уравнение cos 4x = 4a -3 имеет решение. Получим
Значит, уравнение cos 4x = 4a -3 имеет решение. Получим
4х = 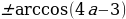 + 2
+ 2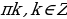 . От куда
. От куда
х = 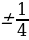
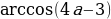 +
+ 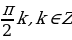 .
.
4) Если а=1, то уравнение cos2 2x = 2a – a принимает вид cos2 2x =1. Из этого уравнения находим х = 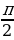 k,
k, 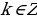
5) Если а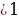 , то 2а -1
, то 2а -1 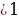 и уравнение cos 4x = 4a -3 не имеет корней.
и уравнение cos 4x = 4a -3 не имеет корней.
Затем, что если а =  или а = 1, то решение тоже можно записать в виде
или а = 1, то решение тоже можно записать в виде
х = 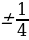
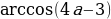 +
+ 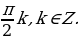
Ответ: 1) Если а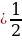 и а
и а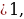 то корней нет.
то корней нет.
2) Если 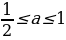 , то х =
, то х = 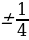
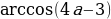 +
+ 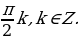
Пример№4:Решим уравнение (а-1)sin2 x – 2(a+1)sin x +2a – 1=0.
Положим y=sin x, тогда данное уравнение примет вид
(a-1)y2 – 2 (a+1)y + 2a-1=0. Первым контрольным значением параметра а будет значение а=1, которое обращает в нуль коэффициент при у2. При а=1 уравнение (a-1)y2 – 2 (a+1)y + 2a-1=0 принимает вид -4у + 1 =0, откуда находим у=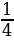 , то есть sin x=
, то есть sin x=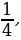 и, следовательно, х = (-1)k arcsin
и, следовательно, х = (-1)k arcsin 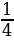 +
+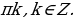 Рассмотри теперь случай, когда а
Рассмотри теперь случай, когда а 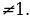 Найдем дискриминант уравнения
Найдем дискриминант уравнения
(a-1)y2 – 2 (a+1)y + 2a-1=0. Имеем: 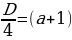 2-(a-1)(2a-1) = -a2 + 5a. Вторыми контрольными значениями параметра а будут те значения, при которых D=0. Это будут значения а=0, а=5. Заметим, что D
2-(a-1)(2a-1) = -a2 + 5a. Вторыми контрольными значениями параметра а будут те значения, при которых D=0. Это будут значения а=0, а=5. Заметим, что D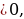 если а
если а или а
или а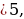 и D
и D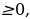 если 0
если 0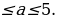 Значит, нам нужно рассмотреть уравнение
Значит, нам нужно рассмотреть уравнение
(a-1)y2 – 2 (a+1)y + 2a-1=0 в каждом из следующих случаев: а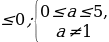 ;
;
а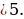
Если а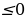 или а
или а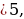 уравнение (a-1)y2 – 2 (a+1)y + 2a-1= 0 не имеет корней.
уравнение (a-1)y2 – 2 (a+1)y + 2a-1= 0 не имеет корней.
В случае 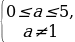 уравнение имеет два действительных корня
уравнение имеет два действительных корня
у1,2 = 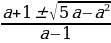 . Так как у = sin x, то должны выполняться следующие двойные неравенства: -1
. Так как у = sin x, то должны выполняться следующие двойные неравенства: -1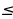 у1
у1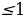 , -1
, -1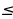 у2
у2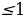 . Нетрудно заметить, что у1=
. Нетрудно заметить, что у1=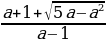 удовлетворяет двойному неравенству -1
удовлетворяет двойному неравенству -1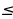 у1
у1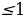 лишь при а=0. В самом деле, если а=0, то у=-1; если а
лишь при а=0. В самом деле, если а=0, то у=-1; если а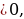 то а+1
то а+1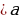 -1 и тем более а+1+
-1 и тем более а+1+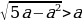 -1, то есть у1
-1, то есть у1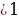 . Если а=0, то уравнение sin x = y1, принимает вид sin x = -1, откуда находим х = -
. Если а=0, то уравнение sin x = y1, принимает вид sin x = -1, откуда находим х = -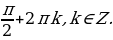 Будем теперь искать значение параметра а
Будем теперь искать значение параметра а
( из рассматриваемого множества системы 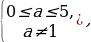 которые удовлетворяют системе неравенств -1
которые удовлетворяют системе неравенств -1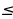 у2
у2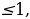 то есть системе
то есть системе
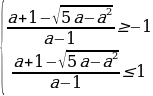
Система в свою очередь, равносильна следующей совокупности систем неравенств:
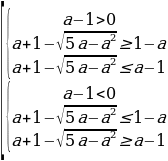
Решим первую систему из данной совокупности. Имеем:
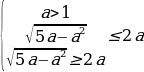
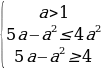
Откуда находим 1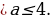 Решим вторую систему совокупности. Имеем:
Решим вторую систему совокупности. Имеем:
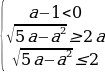
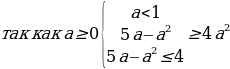 откуда находим 0
откуда находим 0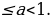
Итак, совокупность систем, а следовательно, и система имеют решения: 0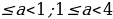 . Это означает, что на множестве
. Это означает, что на множестве 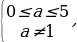 уравнение
уравнение
sin x = 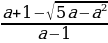 имеет решение только в том случае, если
имеет решение только в том случае, если 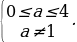 Это решение таково: х = (-1)k arcsin
Это решение таково: х = (-1)k arcsin 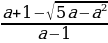 +
+ 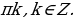 Заметим. что эта запись включает в себя и рассмотренный выше случай, когда а=0. Если 4
Заметим. что эта запись включает в себя и рассмотренный выше случай, когда а=0. Если 4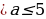 , то уравнение sin x =
, то уравнение sin x = 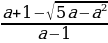 , а с ним и уравнение
, а с ним и уравнение
(а-1)sin2 x – 2(a+1)sin x +2a – 1=0 не имеют корней.
Ответ: 1) если а=1, то х = (-1)k 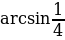 +
+ 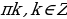
2) если 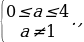 то х = (-1)k arcsin
то х = (-1)k arcsin 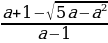 +
+ 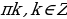
3) если а 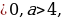 то уравнение не имеет корней
то уравнение не имеет корней
Пример№5: При каких значениях параметра а графики функций
y = sin2 x + acos x и y = 3a – 2a2 не имеют общих точек?
Другими словами, нужно найти такие значения параметра а, при которых уравнение sin2 x + acos x = 3a – 2a2 не имеет корней.
1 – cos2 x + acos x + 2a2 – 3a = 0;
cos2 x – acos x – (2a2 – 3a + 1) = 0.
Введем новую переменную: t = cos x, t 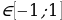 , тогда тригонометрическое уравнение примет вид t2 – at – (2a2 – 3a + 1) = 0. Получили квадратное уравнение с параметром а.
, тогда тригонометрическое уравнение примет вид t2 – at – (2a2 – 3a + 1) = 0. Получили квадратное уравнение с параметром а.
D = a2 + 4(2a2 – 3a + 1) = a2 + 8a2 – 12a + 4 = 9a2 – 12a + 4 = (3a – 2)2,
t1,2 = 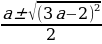 =
= 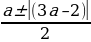 . t1 =
. t1 = 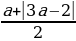 t2 =
t2 = 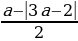
Так как 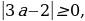 то t1
то t1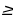 t2
t2
Случай 1. t1 t2 , тогда
t2 , тогда 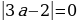 , а =
, а = 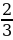 и t2 =
и t2 = 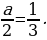 В этом случае уравнение cos x =
В этом случае уравнение cos x = 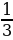 имеет корни.
имеет корни.
Случай 2. t1 t2 . Чтобы уравнения сos x = t1 и сos x = t2 не имели корней необходимо и достаточно выполнения одного из трех условий: t1 2 1,
t2 . Чтобы уравнения сos x = t1 и сos x = t2 не имели корней необходимо и достаточно выполнения одного из трех условий: t1 2 1,
t2 1 1. Рассмотрим каждое из этих условий.
Условие 1. t1 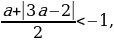
а +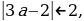
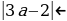 а – 2,
а – 2,
2 + а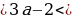 - а – 2,
- а – 2,
4 + а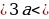 - а.
- а.
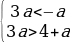
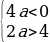
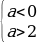
Система решений не имеет, значит, не существует таких значений а, при которых выполняется условие t1
Условие 2. t2 1.
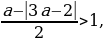
а -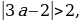
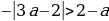 ,
,
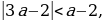
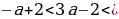 а – 2,
а – 2,
- а + 4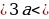 а.
а.
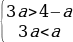
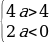
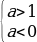
Система решений не имеет, следовательно, не существует таких значений а, при которых выполняется условие t2 1.
Условие 3. t2 1 1.
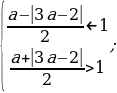
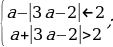
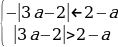 ;
; 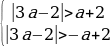 ;
;
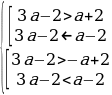 ;
; 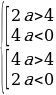 ;
; 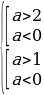 ;
; 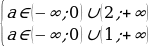
Таким образом, 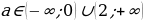 .
.
Ответ: Графики функций y = sin2 x + acos x и y = 3a – 2a2 не имеют общих точек, если 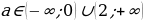 .
.
2.2 Решение тригонометрических неравенств с параметром
Пример№6: Найдите все значения параметра а, при каждом из которых множество решений неравенства 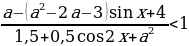 содержит отрезок
содержит отрезок 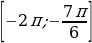 .
.
Заметим, что при любых значениях переменной x и параметра a знаменатель дроби в левой части неравенства положителен, поэтому исходное неравенство равносильно неравенству
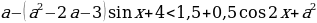 Для того, чтобы множество решений неравенства содержало отрезок
Для того, чтобы множество решений неравенства содержало отрезок 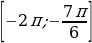 синус должен принимать значения 0
синус должен принимать значения 0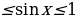 (рис.5).
(рис.5).
Пусть sin x = t, тогда cos 2x =1-2t2и неравенство принимает вид
a – (a2 – 2a -3)t + 4 0,5(1-2t2) + a2 +1,5
0,5(1-2t2) + a2 +1,5
t2 – (a2 – 2a -3)t – a2 + a + 2 
Введем функцию f(t) = t2 – (a2 – 2a -3)t – a2 + a + 2
(рис. 5)
Для того, чтобы множество решений неравенства
t2 – (a2 – 2a -3)t – a2 + a + 2  содержало отрезок
содержало отрезок 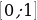 необходимо и достаточно, чтобы одновременно выполнялись два условия f(0)
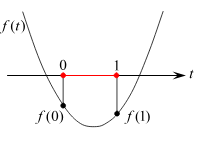
необходимо и достаточно, чтобы одновременно выполнялись два условия f(0)  и f(1)
и f(1)  (рис.6).
(рис.6).
(рис. 6)

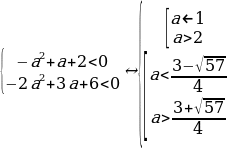

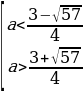
Ответ: 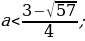
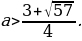
Пример№7: Найдите все значения параметра a, при которых для любого действительного x выполнено неравенство
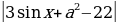 +
+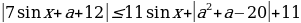 .
.
Пусть t=sin x, тогда неравенство запишется в виде
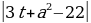 +
+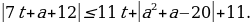
Поскольку -1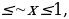 нам требуется найти все значения a, при которых неравенство выполнено при -1
нам требуется найти все значения a, при которых неравенство выполнено при -1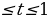 .
.
Рассмотрим функции f(t)= 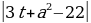 +
+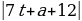 и
и
g(t) = 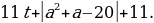 Функция f(t) — кусочно-линейная. Угловой коэффициент её звеньев не превосходит 10. Функция g(t)— линейная функция с угловым коэффициентом 11. Значит, функция g(t) - f(t) возрастающая. Таким образом, если неравенство f(t)
Функция f(t) — кусочно-линейная. Угловой коэффициент её звеньев не превосходит 10. Функция g(t)— линейная функция с угловым коэффициентом 11. Значит, функция g(t) - f(t) возрастающая. Таким образом, если неравенство f(t)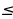 g(t) выполнено при t= - 1, то оно выполнено при t
g(t) выполнено при t= - 1, то оно выполнено при t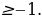 При t = -1 неравенство принимает вид:
При t = -1 неравенство принимает вид:
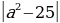 +
+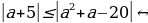
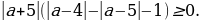
Выражение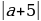 равно 0 при а= - 5 и больше при 0 при других значениях a. Выражение
равно 0 при а= - 5 и больше при 0 при других значениях a. Выражение 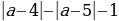 при а
при а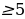 равно 0, при
равно 0, при
4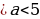 принимает вид 2а – 10, при а
принимает вид 2а – 10, при а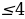 равно −2. Таким образом, неравенство
равно −2. Таким образом, неравенство 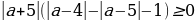 выполнено при
выполнено при 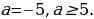
Ответ: 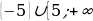 ).
).
Пример№8: Найдите все значения параметра а, при которых для любого действительного значения х выполнено неравенство
2а – 4 + а(3 – sin2 x)2 + cos2x ОДЗ: х ∈R, a ∈R. Пусть sin2 x = t, | t | ≤ 1
2а – 4 + а(3 – t)2 + 1 - t at2 – (6a + 1) + 11a – 3 Найдем все значения параметра а, при которых f(t) = at2 – (6a + 1) + 11a – 3 будет отрицательным при любом | t | ≤ 1.
1) а = 0, f(t) = - t – 3 меньше нуля для любых | t | ≤ 1
2) а 0, 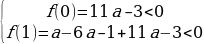 ;
; 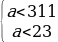 ; 0
; 0
3) а а) D = 1 + 24а – 8а2
а б) t1 ≤ t2 а D ≥ 0,
t0 = 6a+12af(0) = 11а – 3 a≤0.
в) 1 t1 ≤ t2
а D ≥ 0,
6a+12a1,
f(1) = 6а – 4 ⊘
Ответ: а ∈ (-∞; 311).
Пример№9: Найдите все значения параметра а, при каждом из которых множество решений неравенства 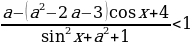 содержит отрезок
содержит отрезок 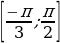 .
.
Заметим, что при любых значениях переменной x и параметра a знаменатель дроби в левой части неравенства положителен, поэтому исходное неравенство равносильно неравенству
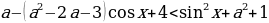 Для того, чтобы множество решений неравенства содержало отрезок
Для того, чтобы множество решений неравенства содержало отрезок 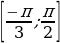 косинус должен принимать значения 0
косинус должен принимать значения 0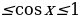 (рис.7).
(рис.7).
Пусть cos x = t, тогда sin 2x =1-2t2 и неравенство принимает вид
a – (a2 – 2a -3)t + 4 1- t2 +a2+1
1- t2 +a2+1
t2 – (a2 – 2a -3)t – a2 + a + 2 
Введем функцию f(t) = t2 – (a2 – 2a -3)t – a2 + a + 2
(рис. 7)
Для того, чтобы множество решений неравенства
t2 – (a2 – 2a -3)t – a2 + a + 2  содержало отрезок
содержало отрезок 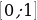 необходимо и достаточно, чтобы одновременно выполнялись два условия f(0)
необходимо и достаточно, чтобы одновременно выполнялись два условия f(0)  и f(1)
и f(1)  (рис.8).
(рис.8).

(рис. 8)
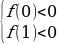

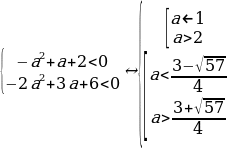

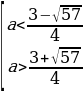
Ответ: 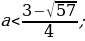
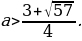
Выводы по второй главе
Во второй главе были приведены решения тригонометрических уравнений и неравенств с параметрами. Рассмотрены пять примеров решения тригонометрических уравнений с параметрами. Задания звучали в двух вариациях: «при каких значения параметра…» и «решите уравнение и найдите значение параметра». Также были разобраны четыре тригонометрических неравенства с параметром. Неравенства, которые были взяты из второй части ЕГЭ, у подобных неравенств задание звучало, не в классическом виде «найдите значение параметра…», а была поставлена дополнительная задача в отборке найденного параметра в заданном отрезке. К каждому примеру было предложено подробный разбор решения.
Заключение
В курсовой работе рассмотрены необходимые для овладения навыков решения тригонометрических уравнений и неравенств с параметрами теоретические основы. Определено понятие параметра, выделены восемь методов решения тригонометрических уравнений: разложение на множители, сведение к квадратным уравнениям, решение однородных уравнений, универсальная подстановка, с помощью замены неизвестного, применение формул понижения степени, с применением формул тройного аргумента. И два метода решения тригонометрических неравенств: геометрический метод и с помощью окружности. Теоритические сведения были проиллюстрированы примерами.
Данные теоритические сведения являются не только вспомогательной теорией для решения тригонометрических уравнений и неравенств с пара-метрами (а так же задания №18 из ЕГЭ), но так же может пригодиться для решения задания №13 из ЕГЭ.
Во второй главе данной работы рассмотрены несколько подходов ре-шения тригонометрических уравнений с параметрами. Их использование может намного упростить решение многих сложных заданий. Можно выде-лить несколько способов решения тригонометрических уравнений с параметрами.
Основные типы задач с параметрами:
• задачи, которые необходимо решить для всех значений параметра или для значений параметра из заданного промежутка. (Примеры 6,9)
• задачи, где требуется найти количество решений в зависимости от значения параметра. (Примеры 1,2,5,7,8)
• задачи, в которых необходимо найти значения параметра, удовлетворяющих некоторым условиям. (Примеры 3,4)
Приведённые примеры дают представление об основных типах задач с параметрами.
Считаю, что цель и задачи, которые поставила перед собой при выполнении курсовой работы, достигнуты. Благодаря отборки теоретических сведений, выделения основных типов тригонометрических уравнений и неравенств с параметрами и изучения различных подходов и методов решения подобных задач произошли сформированность понимания и овладение методами решения основных типов тригонометрических уравнений и неравенств с параметрами.
Список используемых источников
-
Азаров А.И. и др. Тригонометрические уравнения: Учеб. пособие / А.И. Азаров, О.М. Гладун, В.С. Федосенко / - ООО»Тривиум», 2004. -160с.
-
Евдокимова Н.Н. Тригонометрия: Теория и примеры. – СПб: Издательский Дом «Литера», 2005. – 64с.
-
Гусятников Н.В., Гусятников В.В. Учебное пособие «Методы решения уравнений» Екатеринбург, УрГПУ, 2009 г.-56с.
-
Ивлев Б.М. Дидактические материалы по алгебре и началам анализа для 10 класса / Б.М. Ивлев, С.М. Саакян, С.И. Шварцбурд. – 8-е изд. – М.: Просвещение, 2004.-176с.
-
Коноплева О.А. Математика в таблицах: 7-11 классы. – СПб.: «Тригон», 2005. – 104с.
-
Математика. Способы решения экзаменационных задач – 2006. Под редакцией З.С.Стромова. – Волгоград: Братья Гринины, 2006. – 64с.
-
Потапов М.К. Алгебра и начала анализа: дидакт. Материалы для 10 кл./ М.К. Потапов, А.В.Шевкин. – 2-е изд. – М.:Просвещение, 2007. – 159с.
-
Литвиненко В.Н., Мордкович А.Г. Практикум по элементарной математике: Алгебра. Тригонометрия. М.: ABF, 1995. — 352 с.: ил.
-
Бардушкин В., Тригонометрические уравнения. Отбор корней/В. Бардушкин, А. Прокофьев.// Математика, №12, 2005 с. 23--27.
-
Бородин П., Тригонометрия. Материалы вступительных экзаменов в МГУ[текст]/П.Бородин, В.Галкин, В.Панфёров, И.Сергеев, В.Тарасов // Математика №1, 2005 с. 36--48.
-
Выгодский Я.Я., Справочник по элементарной математике. /Выгодский Я.Я. --- М.: Наука, 1970.
-
О. В. Мантуров, Ю. К. Солнцев, Ю. И. Сорокин, Н. Г. Федин - «Толковый словарь математических терминов»
-
Л. Л. Драгилева – «Репетитор по математике», Ростов-на-Дону «Феникс» 1997
-
Далингер, В.А. Задачи с параметрами: учебное пособие / В.А. Далингер. – Омск: Изд-во ООО «Амфора», 2012.
1






 , tg x, обозначил а, в, с для сторон А,В,С для противоположных углов
, tg x, обозначил а, в, с для сторон А,В,С для противоположных углов 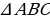 .
. 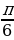
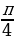
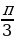
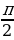

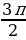

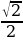
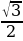
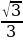
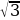
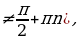
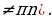
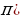 =sin(x-2
=sin(x-2 y)=sin x cos y
y)=sin x cos y 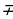 sin x sin y,
sin x sin y,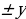 )=
)=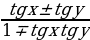 ( x
( x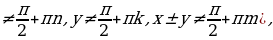
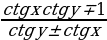 ( x
( x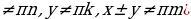 .
. 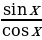 ( x
( x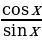 ( x
( x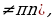
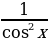 ( x
( x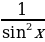 ( x
( x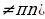 .
. 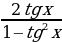 (x
(x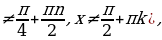
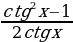 (x
(x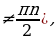
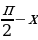
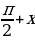
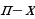
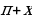
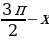
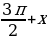
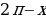
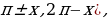 то название функции сохраняется; если дуга х откладывается от вертикального диаметра (
то название функции сохраняется; если дуга х откладывается от вертикального диаметра ( 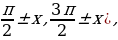 то название функции меняется ( синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс);
то название функции меняется ( синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс); 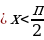 .
.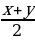 cos
cos 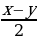 ,
,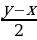 ,
,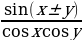 (x
(x
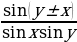 (x
(x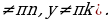
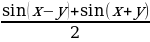 ,
,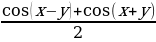 ,
,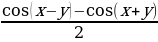 .
. 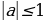
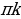
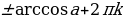
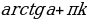
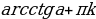
 x =
x = 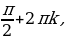
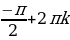 ,
,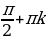 ,
,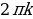 ,
,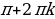 .
.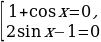
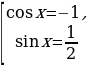
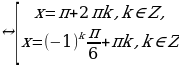
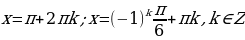
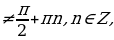
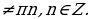
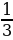 . Затем осуществляем обратную подстановку sin x =
. Затем осуществляем обратную подстановку sin x =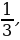 получаем решение исходного уравнения.
получаем решение исходного уравнения.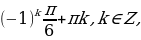 x =
x = 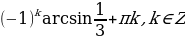
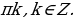
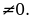 Разделим левую и правую части уравнения на
Разделим левую и правую части уравнения на 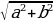 :
: 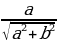 sin x +
sin x +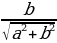 cos x =
cos x = 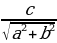 . Так как
. Так как 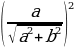 +
+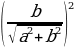 =1, то существует угол
=1, то существует угол 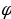 такой, что cos
такой, что cos 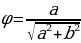 , sin
, sin 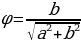 , при этом
, при этом 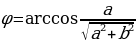 (или
(или 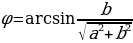 ). Тогда уравнение примет вид sin x cos
). Тогда уравнение примет вид sin x cos 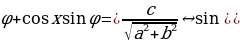 +
+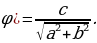
 . Тогда получим
. Тогда получим 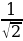 sin x +
sin x + 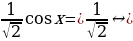 cos
cos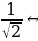
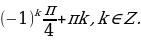
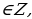 с помощью тригонометрических формул двойного и тройного аргумента, а также формул сложения можно свести двойного и тройного аргумента, а также формул сложения можно свести к рациональному уравнению относительно аргументов sin x, cos x, tg x, ctg x, после чего уравнение может быть сведено к рациональному уравнению относительно t = tg
с помощью тригонометрических формул двойного и тройного аргумента, а также формул сложения можно свести двойного и тройного аргумента, а также формул сложения можно свести к рациональному уравнению относительно аргументов sin x, cos x, tg x, ctg x, после чего уравнение может быть сведено к рациональному уравнению относительно t = tg 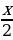 с помощью формул универсальной тригонометрической подстановки
с помощью формул универсальной тригонометрической подстановки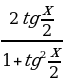 , cos x =
, cos x = 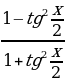 ,
, 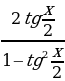 , ctg x =
, ctg x = 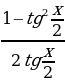 .
. 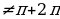 k, k
k, k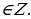 Применив формулы и сделав замену t = tg
Применив формулы и сделав замену t = tg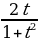 + t = 0, откуда t=0 и, следовательно, x =2
+ t = 0, откуда t=0 и, следовательно, x =2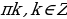 .
. 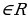
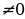 , получим tg x = -1,
, получим tg x = -1, 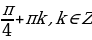
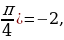 sin (x +
sin (x +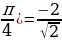 , т.к.
, т.к. 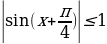 , при х
, при х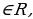 то корней нет
то корней нет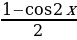 +
+ 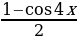 -
- 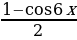 -
- 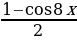 = 0,
= 0,
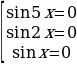
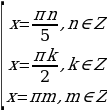
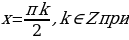 k=2l, l
k=2l, l 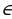 Z содержаться в множестве
Z содержаться в множестве 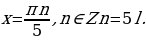
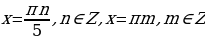
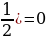 . Последнее уравнение равносильно совокупности двух уравнений:
. Последнее уравнение равносильно совокупности двух уравнений: 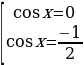
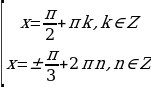
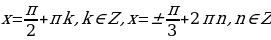
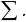 Условимся символом
Условимся символом 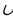 М1М2 обозначать дугу, для которой точка М1 – начальная точка (в обозначении дуги она записывается первой), М2 - конечная точка пути, описываемого текущей точкой по окружности
М1М2 обозначать дугу, для которой точка М1 – начальная точка (в обозначении дуги она записывается первой), М2 - конечная точка пути, описываемого текущей точкой по окружности 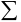 в положительном направлении (против часовой стрелки).
в положительном направлении (против часовой стрелки).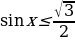

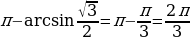
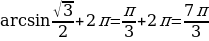
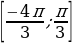 , но так как функцию y=sin x периодическая и имеет период 2
, но так как функцию y=sin x периодическая и имеет период 2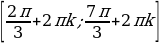 , k
, k
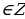
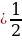

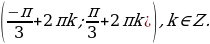
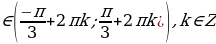
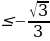
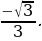 Выделим промежутки, на которых график функции y=ctg x расположен не выше графика прямой y=
Выделим промежутки, на которых график функции y=ctg x расположен не выше графика прямой y=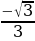 (рис. 4).
(рис. 4).
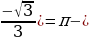 arcctg(
arcctg(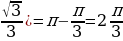
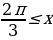
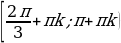 , k
, k . Тогда данное уравнение принимает вид t2 – (а + 2)t – (a + 3) = 0. Чтобы решить получившееся квадратное уравнение с переменной t, найдем его дискриминант: D = a2 + 4a + 4 + + 4a + 12 = a2 + 8a + 16 = (a + 4)2. Так как D≥0, квадратное уравнение имеет решение:
. Тогда данное уравнение принимает вид t2 – (а + 2)t – (a + 3) = 0. Чтобы решить получившееся квадратное уравнение с переменной t, найдем его дискриминант: D = a2 + 4a + 4 + + 4a + 12 = a2 + 8a + 16 = (a + 4)2. Так как D≥0, квадратное уравнение имеет решение: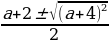 =
= 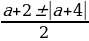 =
= 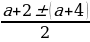
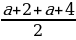 =
= 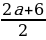 =
= 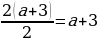
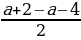 =
= 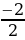 = -1
= -1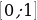 таким образом, заданное нам тригонометрическое уравнение с параметром имеет решение при условии
таким образом, заданное нам тригонометрическое уравнение с параметром имеет решение при условии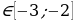 .
.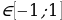 тогда тригонометрическое уравнение примет вид 6t3 – 20t2 + 10 = p. Рассмотрим функцию
тогда тригонометрическое уравнение примет вид 6t3 – 20t2 + 10 = p. Рассмотрим функцию 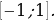 Находим производную: у
Находим производную: у = 18t2 - 40t = 18t (t -
= 18t2 - 40t = 18t (t - 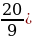 . Определяем критические точки функции: у′=0, 18t(t -
. Определяем критические точки функции: у′=0, 18t(t - 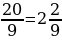 .
.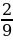 не принадлежит промежутку
не принадлежит промежутку 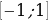 , поэтому вычисляем значения функции в точке 0 и на концах отрезка:
, поэтому вычисляем значения функции в точке 0 и на концах отрезка: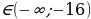
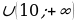 исходное уравнение не имеет корней.
исходное уравнение не имеет корней.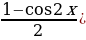 2 + (
2 + (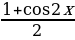 )2 = a, и далее cos2 2x = 2a – a.
)2 = a, и далее cos2 2x = 2a – a.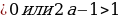 , то уравнение не имеет решений). Если
, то уравнение не имеет решений). Если 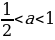 ; 4) а=1; 5) а
; 4) а=1; 5) а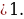
 и уравнение cos2 2x = 2a – a не имеет корней
и уравнение cos2 2x = 2a – a не имеет корней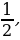 то уравнение cos2 2x = 2a – a принимает вид cos2 2x = 0, откуда находим x =
то уравнение cos2 2x = 2a – a принимает вид cos2 2x = 0, откуда находим x = 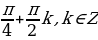
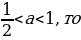 0
0 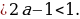 Преобразуем уравнение
Преобразуем уравнение 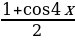 = 2a – 1, и далее cos 4x = 4a -3. Так как в рассматриваемом случае
= 2a – 1, и далее cos 4x = 4a -3. Так как в рассматриваемом случае 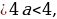 а тогда
а тогда 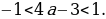 Значит, уравнение cos 4x = 4a -3 имеет решение. Получим
Значит, уравнение cos 4x = 4a -3 имеет решение. Получим 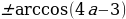 + 2
+ 2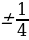
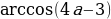 +
+ 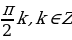 .
. 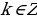
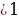 , то 2а -1
, то 2а -1 
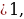 то корней нет.
то корней нет. 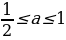 , то х =
, то х = 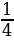 , то есть sin x=
, то есть sin x=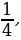 и, следовательно, х = (-1)k arcsin
и, следовательно, х = (-1)k arcsin 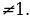 Найдем дискриминант уравнения
Найдем дискриминант уравнения 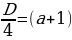 2-(a-1)(2a-1) = -a2 + 5a. Вторыми контрольными значениями параметра а будут те значения, при которых D=0. Это будут значения а=0, а=5. Заметим, что D
2-(a-1)(2a-1) = -a2 + 5a. Вторыми контрольными значениями параметра а будут те значения, при которых D=0. Это будут значения а=0, а=5. Заметим, что D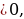 если а
если а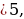 и D
и D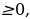 если 0
если 0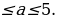 Значит, нам нужно рассмотреть уравнение
Значит, нам нужно рассмотреть уравнение 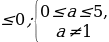 ;
; 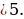
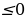 или а
или а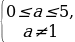 уравнение имеет два действительных корня
уравнение имеет два действительных корня 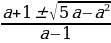 . Так как у = sin x, то должны выполняться следующие двойные неравенства: -1
. Так как у = sin x, то должны выполняться следующие двойные неравенства: -1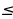 у1
у1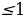 , -1
, -1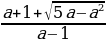 удовлетворяет двойному неравенству -1
удовлетворяет двойному неравенству -1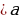 -1 и тем более а+1+
-1 и тем более а+1+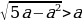 -1, то есть у1
-1, то есть у1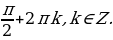 Будем теперь искать значение параметра а
Будем теперь искать значение параметра а 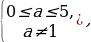 которые удовлетворяют системе неравенств -1
которые удовлетворяют системе неравенств -1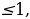 то есть системе
то есть системе 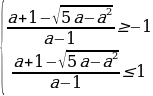
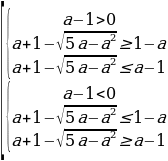
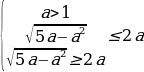
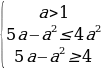
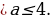 Решим вторую систему совокупности. Имеем:
Решим вторую систему совокупности. Имеем: 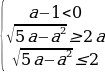
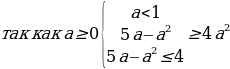 откуда находим 0
откуда находим 0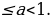
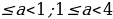 . Это означает, что на множестве
. Это означает, что на множестве 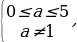 уравнение
уравнение 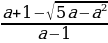 имеет решение только в том случае, если
имеет решение только в том случае, если 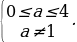 Это решение таково: х = (-1)k arcsin
Это решение таково: х = (-1)k arcsin 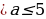 , то уравнение sin x =
, то уравнение sin x = 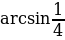 +
+ 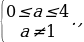 то х = (-1)k arcsin
то х = (-1)k arcsin 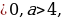 то уравнение не имеет корней
то уравнение не имеет корней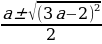 =
= 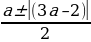 . t1 =
. t1 = 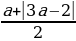 t2 =
t2 = 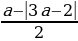
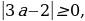 то t1
то t1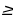 t2
t2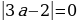 , а =
, а = 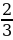 и t2 =
и t2 = 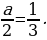 В этом случае уравнение cos x =
В этом случае уравнение cos x = 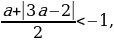
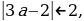
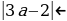 а – 2,
а – 2, 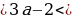 - а – 2,
- а – 2,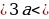 - а.
- а.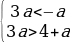
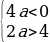
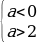
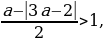
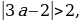
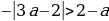 ,
, 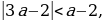
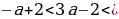 а – 2,
а – 2,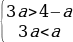
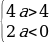
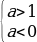
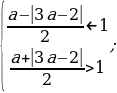
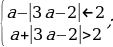
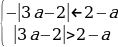 ;
; 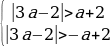 ;
; 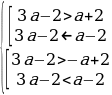 ;
; 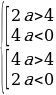 ;
; 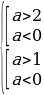 ;
; 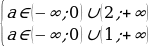
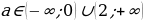 .
.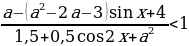 содержит отрезок
содержит отрезок 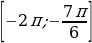 .
.
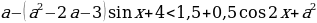 Для того, чтобы множество решений неравенства содержало отрезок
Для того, чтобы множество решений неравенства содержало отрезок 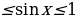 (рис.5).
(рис.5).

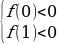
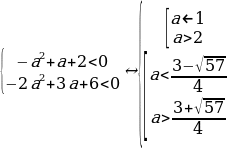
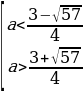
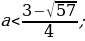
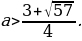
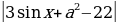 +
+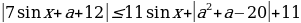 .
.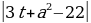 +
+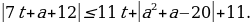
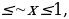 нам требуется найти все значения a, при которых неравенство выполнено при -1
нам требуется найти все значения a, при которых неравенство выполнено при -1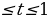 .
. 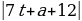 и
и 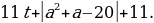 Функция f(t) — кусочно-линейная. Угловой коэффициент её звеньев не превосходит 10. Функция g(t)— линейная функция с угловым коэффициентом 11. Значит, функция g(t) - f(t) возрастающая. Таким образом, если неравенство f(t)
Функция f(t) — кусочно-линейная. Угловой коэффициент её звеньев не превосходит 10. Функция g(t)— линейная функция с угловым коэффициентом 11. Значит, функция g(t) - f(t) возрастающая. Таким образом, если неравенство f(t)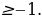 При t = -1 неравенство принимает вид:
При t = -1 неравенство принимает вид: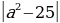 +
+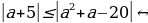
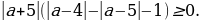
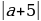 равно 0 при а= - 5 и больше при 0 при других значениях a. Выражение
равно 0 при а= - 5 и больше при 0 при других значениях a. Выражение 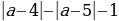 при а
при а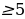 равно 0, при
равно 0, при 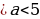 принимает вид 2а – 10, при а
принимает вид 2а – 10, при а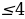 равно −2. Таким образом, неравенство
равно −2. Таким образом, неравенство 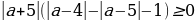 выполнено при
выполнено при 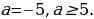
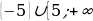 ).
).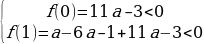 ;
; 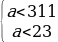 ; 0
; 0 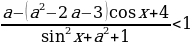 содержит отрезок
содержит отрезок 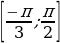 .
.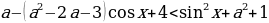 Для того, чтобы множество решений неравенства содержало отрезок
Для того, чтобы множество решений неравенства содержало отрезок 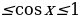 (рис.7).
(рис.7).





















