Научно-практическая конференция исследовательских работ обучающихся муниципальных бюджетных общеобразовательных организаций
г.Шахты
Проектно-исследовательская работа
Тема: «Квадратные уравнения в трудах Диофанта»
секция математики
Выполила: Сыроватская Татьяна Юрьевна,
обучающаяся 8 класса Б
МБОУ г. Шахты «Гимназия им. А.С. Пушкина»
Руководитель: Назарьева Татьяна Николаевна,
учитель математики МБОУ г. Шахты «Гимназия им. А.С. Пушкина»
2020 год
Оглавление. 1. Введение. ………………………………………………………..……..3
2. Основная часть.
2.1. Немного о Диофанте. …………………………………….……4
2.2. Арифметика Диафанта…………………………………………5
2.3. Диофантовы уравнения………………………………………...6
2.4. Как составлял и решал Диофант квадратные уравнения…….9
2.5. Применение диофантовых уравнений………………………..10
3. Заключение. ………………….…………………………………………14
4. Список литературы и источников……………………………………..15
Введение
Почему я выбрала эту тему
С уравнениями мы знакомы давно, но с квадратными уравнениями мы познакомились только в этом году. Меня заинтересовала эта тема, т.к. я и раньше любила решать уравнения. Великого древнегреческого ученого Диофанта мы едва затронули в курсе алгебры. Как оказалось, у Диофанта была своя система решения уравнений и он даже написал 13 книг посвященных этому. Так давайте узнаем о Диофантовых уравнениях поподробнее.
Цели исследования:
Узнать, кто такой Диофант
Изучить тему диофатовых уравнений
Разобраться в решении диофантовых уравнений и их применении.
Гипотеза исследования
Умение решать диофантовы уравнения поможет решать олимпиадные задания, а также подготовиться к решению ряду задач № 19 ЕГЭ.
Задачи исследования:
изучить литературу, интернет-ресурсы;
научиться решать неопределённые уравнения первой степени и квадратные уравнения методом Диофанта, узнать, когда они не имеют решений;
разобрать решение различных задач, в том числе задания №19 ЕГЭ;
обобщить изученный материал, подготовить презентацию.
Основная часть.
Немного о Диофанте.
Диофа́нт Александри́йский (см приложение 1)— древнегреческий математик, живший предположительно в III веке н. э. Нередко упоминается как «отец алгебры». Автор «Арифметики» — книги, посвящённой нахождению положительных рациональных решений неопределённых уравнений. В наше время под «диофантовыми уравнениями» обычно понимают уравнения с целыми коэффициентами, решения которых требуется найти среди целых чисел.
Диофант был первым греческим математиком, который рассматривал дроби наравне с другими числами. Диофант также первым среди античных учёных предложил развитую математическую символику, которая позволяла формулировать полученные им результаты в достаточно компактном виде.
В честь Диофанта назван кратер на видимой стороне Луны.
Диофант представляет одну из наиболее трудных загадок в истории науки. Нам не известны ни время, когда он жил, ни предшественники его, которые работали бы в той же области.
Промежуток времени, когда мог жить Диофант, составляет полтысячелетия! Нижняя грань этого промежутка определяется без труда: в своей книге о многоугольных числах Диофант неоднократно упоминает математика Гипсикла Александрийского, который жил в середине II века до н. э. С другой стороны, в комментариях Теона Александрийского к «Альмагесту» знаменитого астронома Птолемея помещён отрывок из сочинения Диофанта. Теон жил в середине IV века н. э. Этим определяется верхняя грань этого промежутка. Итак, 500 лет! Зато место жительства Диофанта хорошо известно — это знаменитая Александрия, центр научной мысли эллинистического мира.
В одном из древних рукописных сборников задач в стихах жизнь Диофанта описывается в виде следующей алгебраической загадки, представляющей надгробную надпись на его могиле:
Прах Диофанта гробница покоит; дивись ей — и камень
Мудрым искусством его скажет усопшего век.
Волей богов шестую часть жизни он прожил ребёнком
И половину шестой встретил с пушком на щеках.
Только минула седьмая, с подругою он обручился.
С нею пять лет проведя, сына дождался мудрец;
Только полжизни отцовской возлюбленный сын его прожил.
Отнят он был у отца ранней могилой своей.
Дважды два года родитель оплакивал тяжкое горе,
Тут и увидел предел жизни печальной своей.
Она эквивалентна решению следующего уравнения:
{\displaystyle x={\frac {x}{6}}+{\frac {x}{12}}+{\frac {x}{7}}+5+{\frac {x}{2}}+4}![]()
![]() х=
х=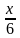 +
+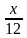 +
+ 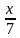 + 5 +
+ 5 + 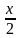 + 4
+ 4
Отсюда нетрудно подсчитать, что Диофант прожил 84 года.
Арифметика Диафанта
Основное произведение Диофанта — Арифметика в 13 книгах. К сожалению, сохранились только 6 первых книг из 13.
Лист из Арифметики (рукопись XIV века). В верхней строке записано уравнение (см. приложение2)
Первая книга предварена обширным введением, в котором описаны используемые Диофантом обозначения. Неизвестную Диофант называет «числом» (ἀριθμός) и обозначает буквой ς, квадрат неизвестной — символом ΔΥ (сокращение от δύναμις — «степень»), куб неизвестной — символом ΚΥ (сокращение от κύβος — «куб»). Предусмотрены специальные знаки для следующих степеней неизвестного, вплоть до шестой, называемой кубо-кубом, и для противоположных им степеней, вплоть до минус шестой.
Знака сложения у Диофанта нет: он просто пишет рядом положительные члены в порядке убывания степени, причём в каждом члене сначала записывается степень неизвестного, а затем численный коэффициент. Вычитаемые члены также записываются рядом, а перед всей их группой ставится специальный знак в виде перевёрнутой буквы Ψ. Знак равенства обозначается двумя буквами ἴσ (сокращение от ἴσος — «равный»).
Сформулированы правило приведения подобных членов и правило прибавления или вычитания к обеим частям уравнения одного и того же числа или выражения: то, что потом у ал-Хорезми стало называться «алгеброй и алмукабалой». Введено правило знаков: «минус на плюс даёт минус», «минус на минус даёт плюс»; это правило используется при перемножении двух выражений с вычитаемыми членами. Всё это формулируется в общем виде, без отсылки к геометрическим истолкованиям.
Бо́льшая часть труда — это сборник задач с решениями (в сохранившихся шести книгах их всего 189), умело подобранных для иллюстрации общих методов. Главная проблематика Арифметики — нахождение положительных рациональных решений неопределённых уравнений. Рациональные числа трактуются Диофантом так же, как и натуральные, что не типично для античных математиков.
Сначала Диофант исследует системы уравнений второго порядка от двух неизвестных; он указывает метод нахождения других решений, если одно уже известно. Затем аналогичные методы он применяет к уравнениям высших степеней. В VI книге исследуются задачи, относящиеся к прямоугольным треугольникам с рациональными сторонами.
Диофантовы уравнения
Диофантовы уравнения – алгебраические уравнения или системы алгебраических уравнений с целыми коэффициентами, для которых надо найти целые или рациональные решения. При этом число неизвестных в уравнениях больше числа уравнений.
Диофант сам находил решения своих задач. Вот несколько задач из его «Арифметики».
1. Найти два числа так, чтобы их произведение находилось в заданном отношении к их сумме.
2. Найти три квадрата так, чтобы сумма их квадратов тоже была квадратом.
3. Найти два числа так, чтобы их произведение делалось кубом как при прибавлении , так и при вычитании их суммы.
4. Для числа 13=2²+3² найти два других, сумма квадратов которых равна 13.
Приведём диофантово решение последней задачи. Он полагает первое число (обозначим его через А) равным x+2, а второе число B равным 2x-3 , указывая , что коэффициент перед x можно взять и другой. Решая уравнения
(x+2)²+(kx-3)²=13,
Диофант находит x=8/5, откуда A=18/5,B=1/5. Воспользуемся указанием Диофанта и возьмём произвольный коэффициент перед x в выражении для B. Пусть снова А=x+2,а В=kx-3, тогда из уравнения
(x+2)²+(kx-3)²=13
x=2(3k-2)/k²+1.
Отсюда
А=2(k²+3k-1)/k²+1,
В=3k²-4k-3/k²+1.
Теперь становятся понятными рассуждения Диофанта. Он вводит очень удобную подстановку А=x+2, В=2x-3, которая с учётом условия 2²+3²=13 позволяет понизить степень квадратного уравнения. Можно было бы с тем же успехом в качестве В взять 2x+3 , но тогда получаются отрицательные значения для В, чего Диофант не допускал. Очевидно, k=2- наименьшее натуральное число , при котором А и В положительны .
Исследование Дифантовых уравнений обычно связано с большими трудностями. Более того, можно указать многочлен F (x,y1,y2 ,…,yn) c целыми коэффициентами такой, что не существует алгоритма , позволяющего по любому целому числу x узнавать , разрешимо ли уравнение F (x,y1,y2 ,…,yn)=0 относительно y1,…,y. Примеры таких многочленов можно выписать явно. Для них невозможно дать исчерпывающего описания решений.
Современной постановкой диофантовых задач мы обязаны Ферма. Именно он поставил перед европейскими математиками вопрос о решении неопределённых уравнений только в целых числах. Надо сказать, что это не было изобретением Ферма - он только возродил интерес к поиску целочисленных решений. А вообще задачи, допускающие только целые решения, были распространены во многих странах в очень далёкие от нас времена. В нынешней математике существует целое направление, занимающееся исследованиями диофантовых уравнений, поиском способов их решений. Называется оно диофантовым анализом и диофантовой геометрией, поскольку использует геометрические способы доказательств.
Простейшее Диофантово уравнение ax+by=1,где a и b – цельные взаимопростые числа, имеет бесконечно много решений (если x0 и y0-решение, то числа x=x0+bn, y=y0-an, где n- любое целое , тоже будут решениями). Рассмотрим простое диофантово уравнение
5х-8у=19
Найдем частное решение методом подбора х=7, у=2.
1)5 х - 8 у=19;
2)5·7-8·2=19;
Вычтем из уравнения 1) второе равенство, получим
5(х-7)-8(у-2)=0
5(х-7)=8(у-2)
5 и 8 взаимно простые (НОД=1), 5 не делится на 8, следовательно делится на (х-7)
x-7=8k, k-целое.
x=8k+7, подставим
5(8k+7-7)=8(y-2)
5·8k=8· (y-2)
5k=y-2;
y=5k+2.
Ответ:(8k+7;5k+2)
Существует более удобный способ подбора частного решения.
Решаем это уравнение относительно того из неизвестных, при котором наименьший (по модулю) коэффициент. 5х - 8у = 19 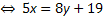
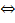 х =
х = 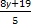 .
.
Остатки при делении на 5: 0,1,2,3,4. Подставим вместо у эти числа.
Если у = 0, то х = 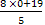 =
=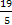 .
.
Если у =1, то х = 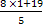 =
=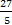 .
.
Если у = 2, то х = 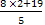 =
=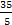 = 7
= 7 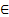 Z.
Z.
Если у =3, то х = 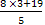 =
=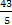 .
.
Если у = 4 то х = 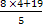 =
=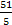 .
.
Итак, частным решением является пара (7;2).
Тогда общее решение: 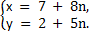 n
n 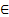 Z.
Z.
Диофантовы уравнения могут и не могут иметь решение.
Пример: 35х+28y=25
7(5x+4y)=25
7(5x+4y) делится на 7, а 25 не делится на 7, т.к. эти части равны, такого быть не может, получили противоречие, значит это уравнение не имеет решений. Мы рассмотрели множество таких уравнений и пришли к выводу, что уравнение вида ax+by=c, не имеют решение, если a и b делятся на целое число d, а с не делится на d, то диофантовое уравнение не имеет решений.
Другим примером Диофантовых уравнений является
x2 + у2 = z2 .
Это Диофантово уравнение 2-й степени. Сейчас мы займёмся поиском его решений. Удобно записывать их в виде троек чисел (x,y,z). Они называются пифагоровыми тройками. Вообще говоря, уравнению удовлетворяет бесконечное множество решений. Но нас будут интересовать только натуральные. Целые, положительные решения этого уравнения представляют длины катетов х, у и гипотенузы z прямоугольных треугольников с целочисленными длинами сторон и называются пифагоровыми числами. Наша задача состоит в том, чтобы найти все тройки пифагоровых чисел. Заметим, что если два числа из такой тройки имеют общий делитель, то на него делится и третье число. Поделив их все на общий делитель, вновь получим пифагороау тройку. Значит от любой пифагоровой тройки можно перейти к другой пифагоровой тройке, числа которой попарно взаимо просты. Такую тройку называют примитивной. Очевидно, для поставленной нами задачи достаточно найти общий вид примитивних пифагоровых троек. Ясно, что в примитивной пифагоровой тройке два числа не могут быть чётными, но в то же время все три числа не могут быть нечётными одновременно. Остаётся один вариант: два числа нечётные, а одно чётное. Покажем, что z не может быть чётным числом. Предположим противное: z=2m, тогда x и y-нечётные числа. x=2k+1, y=2t+1. В этом случае сумма x²+y²=4(k²+k+t²+t)+2 не делится на 4, в то время как z²=4m² делится на 4. Итак, чётным числом является либо x, либо y. Пусть x=2u, y и z- нечётные числа. Обозначим z+y=2v, z-y=2w . Числа v и w взаимно простые. На самом деле, если бы они имели общий делитель d1, то он был бы делителем и для z=w+v, и для y=v-w, что противоречит взаимной простоте y и z. Кроме того , v и w разной чётности: иначе бы y и z были бы чётными. Из равенства x²=(z+y)(z-y) следует, что u²=vw. Поскольку v и w взаимно просты, а их произведение является квадратом , то каждый из множителей является квадратом . Значит найдутся такие натуральные числа p и q, что v=p², w= q² . Очевидно, числа p и q взаимно просты и имеют разную чётность . Теперь имеем
z=p²+q² , y=p²-q²,
откуда
x²=( p²+q²)²-( p²-q²)²=4 p² q².
В результате мы доказали, что для любой примитивной пифагоровой тройки (x,y,z) найдутся взаимо простые натуральные числа p и q разной чётности , pq , такие, что
х =2pq, у =p²-q², z = p2 + q2 .(6)
Все тройки взаимно простых пифагоровых чисел можно получить по формулам
х =2pq, у = p²-q², z = p2 + q2 ,
где m и n — целые взаимо простые числа. Все остальные его натуральные решения имеют вид:
x=2kpq,y=k(p²-q²),z=k(p2 + q2 ),
где k-произвольное натуральное число
Как составлял и решал Диофант квадратные уравнения
В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.
При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.
Вот, к примеру, одна из его задач.
Задача 11. «Найти два числа, зная, что их сумма равна 20, а произведение — 96».
Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так как если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т. е. 10 + х, другое же меньше, т. е 10 - х. Разность между ними 2х. Отсюда уравнение
(10+x)(10—x) =96,
или же
100 —x2 = 96.
x2 - 4 = 0
Отсюда х = 2. Одно из искомых чисел равно 12, другое 8. Решение х = - 2 для Диофанта не существует, так как греческая математика знала только положительные числа.
Если мы решим эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то мы придем к решению уравнения
y(20-y)=96
y2 - 20y+96=0
Ясно, что, выбирая в качестве неизвестного полуразность искомых чисел, Диофант упрощает решение; ему удается свести задачу к решению неполного квадратного уравнения
Применение диофантовых уравнений.
Диофантовы уравнения в олимпиадных задачах
Диофантовы уравнения в экономике
Задача 1. Как, имея монеты в 5 копеек и в 3 копейки, заплатить кассиру в магазине 13 копеек?
Решение: х - количество монет по 5 коп., у- количество монет по 3 коп. Составим и решим уравнение 5х + 3у= 13. Подберём частное решение х=2, у=1, тогда 5·2+3·1=13,
5х + 3у = 5·2+3·1, перенесём все слагаемые в левую часть и сгруппируем
5·(х-2) + 3·(у-1) =0, обозначим х-2 = х1, у-1 = у1, тогда уравнение становиться однородным, 5х1+3у1=0, отсюда  , у1 кратно 5, т.е. у1 =5n, х1 = -3n, где n- любое целое число, вернёмся к старым неизвестным х-2= -3n , х= 2-3n,
, у1 кратно 5, т.е. у1 =5n, х1 = -3n, где n- любое целое число, вернёмся к старым неизвестным х-2= -3n , х= 2-3n,
у-1= 5n, у =1+ 5n .
Ответ: х= 2-3n, у =1+ 5n , где n- любое целое число.
Замечание: Если х будет отрицательным, это значит сдача, т.е. продавец должна будет вернуть.
Задача. 2. Для перевозки зерна имеются мешки, в которые входит либо 60 кг, либо 80 кг зерна. Сколько надо заготовить тех и других мешков для загрузки 1 т зерна таким образом, чтобы все мешки были полными? Какое наименьшее количество мешков при этом может понадобиться?
Решение: Для неизвестных х и у , обозначающих количество мешков по 60 и по 80 кг соответственно, имеем уравнение 60х+80у=1000, сократив обе части уравнения получим 3 х+5 у =50. Надо решить это уравнение в целых неотрицательных числах. Одно целочисленное решение этого уравнения
(-50;50), действительно 3·(-50)+4·50 = 50.
3 х+5 у = 3·(-50)+4·50 , 3( х+50)+5( у-50)=0,
х=4n-50, у=50-3n, где n- любое целое число.
Так как число мешков неотрицательно, то 4n-50 ≥0 и 50-3n ≥0, значит
| Значение n | Значение х | Значение у | х+у |
| 13 | 2 | 11 | 13наименьшее |
| 14 | 6 | 8 | 14 |
| 15 | 10 | 5 | 15 |
| 16 | 14 | 2 | 16 |
Ответ: 13 мешков, 2 мешка по 60 кг, 11 мешков по 80 кг
Задача 3. Требуется разлить 20,5 литра сока в банки по 0,7л и 0,9 л, так, чтобы все банки оказались полными. Сколько каких банок надо заготовить? Какое наименьшее количество банок при этом может понадобиться?
Решение: Задача сводится к решению уравнения
0,7х+09у= 20,5 в целых неотрицательных числах , где х и у – количество банок по 0,7л и 0,9л соответственно.
Преобразуем уравнение к виду 7 х+9 у = 205 , а затем, делая последовательные замены переменных в левой части, получим равенства
7 х+9 у =7(х+ у)+2у= 7u+2у= u+2(у+3u) =u+2v= 205, где х+у=u, у+3u = v.
Из этих равенств имеем
u = 205-2v, у = v - 3u = v- 3(205-2v)=7v- 615 ≥ 0, х =u-у = 205-2v- (7v-615)= 820-9v ≥0.
| v | х | у | х+у |
| 88 | 28 | 1 | 29 |
| 89 | 19 | 8 | 27 |
| 90 | 10 | 15 | 25 |
| 91 | 1 | 22 | 23- наименьшая |
Ответ: 23 банки, из них 1 по 0,7л и 22 банки по 0,9 л.
Задача 4. ( старинная )
Двенадцать человек несут 12 хлебов; каждый мужчина несёт по 2 хлеба, женщина – по половине хлеба, ребёнок – по четверти хлеба. Сколько было мужчин, женщин и детей?
Решение: Пусть было х мужчин, у женщин, тогда детей было 12- х – у. Вместе они несли  хлебов. Составим уравнение
хлебов. Составим уравнение
 .
.
Умножим правую и левую части этого уравнения на 4 , после преобразований получим равносильное ему уравнение
7х+у = 36,
имеющий частное решение х=5, у=1 и общее решение х = 5- n,
у = 1+7n, где n- любое целое число.
Чтобы х и у и (12-х-у) были натуральными числами, можно взять только одно значение n , равное 0. При этом х = 5, у = 1, 12 – х –у = 6, т.е. было 5 мужчин,1 женщина, 6 детей.
Ответ: было 5 мужчин,1 женщина, 6 детей.
Применение в истории
Стоит упомянуть одно интересное историческое приложение, использующее свойства диофантовых уравнений. Согласно некоторым источникам, китайские военачальники, чтобы узнать численность своей армии, давали несколько последовательных команд «В колонну по 7 становись!», «В колонну по 11 становись!», «В колонну по 13 становись!», «В колонну по 17 становись!» и в каждом случае выясняли, сколько солдат получилось в последнем ряду. После этого (только по полученным остаткам!) вычислялось общее количество солдат.
Диофантовы уравнения в КИМах ЕГЭ
Вариант № 144 А.Ларин, задание № 19
Заключение
В разных учебниках встречаются многие старинные задачи, которые можно решить с помощью уравнений Диофанта, в т.ч. некоторые прототипы задания № 19 профильного ЕГЭ.. Выполнив данный проект, я научилась находить целые решения линейных уравнений с двумя неизвестными , поняла, что существуют жизненные ситуации, когда необходимо решить уравнение с несколькими неизвестными в целых числах, помимо этого увидела, что спектр применения данных уравнений очень широк. В дальнейшем мне бы хотелось расширить мое исследование и рассмотреть решение диофантовых уравнений более высокого порядка, в том числе великую теорему Ферма.
Список литературы и источников.
Башмакова И.Г., Диофант и Диофантовы уравнения. - М.: «Наука», 1972г.
Соловьев Ю.Н., Неопределенные уравнения первой степени: Квант, 1992 г.
Стройк Д.Я., Краткий очерк истории математики. - М.: «Наука», 1990 г.
http://www.newreferat.com/ref-21974-2.html
https://ru.wikipedia.org/wiki/Диофант_Александрийский
http://www.bestreferat.ru/referat-412475.html
http://ega-math.narod.ru/Liv/Diophant.htm#ch04
http://www.cleverstudents.ru/equations/quadratic_equations.html
https://ru.wikipedia.org/wiki/Диофантово_уравнение
http://mirznanii.com/a/313605-1/diofantovye-uravneniya
Приложения:
1
2







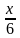 +
+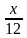 +
+ 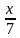 + 5 +
+ 5 + 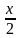 + 4
+ 4





















