Лабораторно-практическая работа № 1 по теме:
«Приложение производной в механике»
Цель работы: отработка понятий «механический и геометрический смысл производной»
Планируемые результаты:
Предметные: обучающиеся научатся применять полученные знания при вычислении производных, построении графиков скорости; получат возможность на практике увидеть механический смысл производной
Метапредметные: познавательные – формулировать выводы относительно приложений производной в механике
регулятивные – планировать самостоятельно познавательную деятельность
коммуникативные – выражать логически верные, обоснованные высказывания по теме, работать в парах, группах
Личностные: использовать научные методы при организации собственной познавательной деятельности; проявлять к ней ответственное отношение; представлять результаты групповой деятельности.
Выполнение работы
(часть 1)
А) известен закон прямолинейного движения точки x = x(t) t ͼ [ 0; 10 ]
Б) найти:
Среднюю скорость движения на указанном отрезке времени
Скорость и ускорение в момент времени t0
Моменты остановки, продолжает ли точка после момента остановки движение в том же или противоположном направлении
Наибольшую скорость движения на указанном отрезке времени ( можно построить график скорости)
Сделать вывод
Задания дифференцированы по уровню сложности ( 1 вариант – наименьший уровень сложности)
Варианты (работа в парах или группах)
X (t) = t2 – 3t, t0 = 4
X (t) = t3 + 2t, t0 = 1
X (t) = 2t3 – t2 , t0 = 2
X (t) = t3 - 2t2 + 1, t0 = 2 (разобрать с учащимися)
X (t) = t4 - ½t2 + 1, t0 = 0,5
X (t) = 2t3 – 2,5t2 + 3t + 1 , t0 = 1
X (t) = ( 3- t ) . ( t – t2 ), t0 = 2
X (t) = (t + 2)( t2 – t + 5), t0 = 4
X(t) = (t -1)3 , t0 = 3
X (t) = t4 + t3 + t2 + 4t , t0 = 0,5
X(t) = t4 / 4 + t3 / 3 + 3t2 / 2 + 2t, t0 = 1
X(t) = (6t – 2) / (6t + 2), t0 =1
(часть 2)
Перед началом работы проводится беседа:
Каков физический смысл производной перемещения? (это – скорость)
Можно ли найти производную скорости? Используется ли эта величина в физике? Как она называется? (да; ускорение)
Мгновенная скорость равна 0. Что можно сказать о движении тела в этот момент? (это – остановка тела)
Каков физический смысл следующих высказываний: производная = 0 в точке t0 (тело останавливается) при переходе через точку t0 производная меняет знак? (направление движения меняется на противоположное)
(часть3)
Образец выполнения работы (вариант 4)
X (t) = t3 - 2t2 + 1, t0 = 2 средняя скорость движения точки v ср. = Δх / Δt
Δх = х (10) – х (0) = 1000 – 2 . 1000 + 1 – 1 = 1200; Δt = 10 – 0 = 10
v ср. = 1200 : 10 = 120
v = х1 (t) = (t3 – 2t2 + 1)1 = 3t2 – 4t
v(2) = 3 . 4 – 4 . 2 = 4
v(t) = 0, 3t2 – 4t =0, t(3t – 4) = 0, t1 = 0, t2 = 4/3

Знак производной меняется, т.е. тело движется в противоположном направлении.
Начертим схематически график скорости v(t) = 3t2 – 4t, t ͼ [ 0; 10 ] 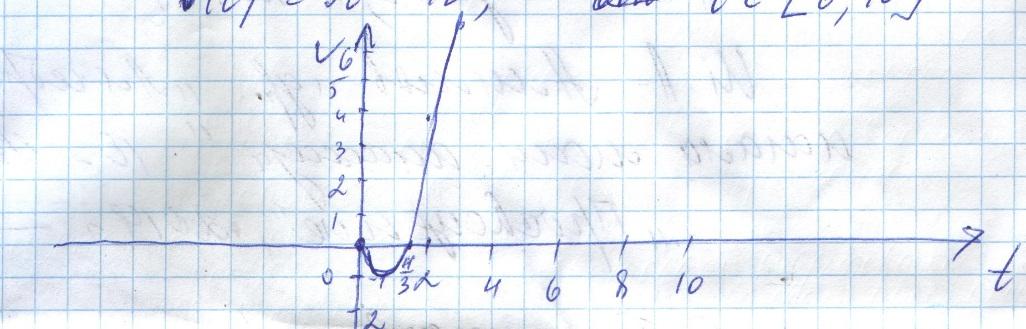
| t | 0 | 1 | 4/3 | 2 | 3 | 10 |
| v | 0 | -1 | 0 | 4 | 15 | 260 |
Наибольшая скорость достигается в точке t = 10 v(10) = 3 . 102 – 4 . 10 = 260
Вывод
В чём состоит механический (физический) смысл производной? Он заключается в том, что…..(производная x1 (t) выражает скорость протекания процесса в момент времени t или что величина, показывающая мгновенную скорость изменения в данной точке)
Вспомните геометрический смысл производной….(значение производной в точке равно угловому коэффициенту касательной к графику функции в этой точке, т.е.
k = tg@ = y1 (x)
ответы:
| Этап | 1 | 2 | 3 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1 | 7 | 102 | 190 | 995 | 178 | 63 | 113 | 73 | 1114 | 3001/3 | 6/31 |
| 2 | 5; 2 | 5; 6 | 20; 22 | 0; 2 | 4; 7 | -1; 7 | 59; 26 | 12; 12 | 6,25; 8 | 7; 8 | 0,375; -9/16 |
| 3 | 1; 5 | - | 0; 1/3 | ½; 0 | - | (4 ± кор.кв.7) / 4 | - | 1 | - | - | - |
| 4 | 17 | 302 | 580 | 3990 | 553 | 223 | 323 | 243 | 4324 | 1132 | 6 |
Литература: А.Г.Мордкович «Алгебра и начала математического анализа» 10-11 кл. «Мнемозина», 2014г.
Ш.А.Алимов и др. «Алгебра и начала математического анализа» 20-11 кл. «Просвещение», 2014г.
М.И.Башмаков «Математика»































