Лекция 12. Понятие предела функции в точке. Теоремы о пределах.

Понятие предела функции в точке. Теоремы о пределах

Преподаватель математики

М. Е. Никитин

Предел функции

Предел – одно из основных по нятий математического анализа. Понятие предела использовалось еще Ньютоном во второй половине XVII века и математиками XVIII века, такими как Эйлер и Лагранж, однако они понимали предел интуитивно. Первые строгие определения предела дали Больцано в 1816 году и Коши в 1821 году.

Лагранж

Ньютон

Эйлер

Больцано

Коши

Различают – предел функции в точке и предел функции на бесконечности .

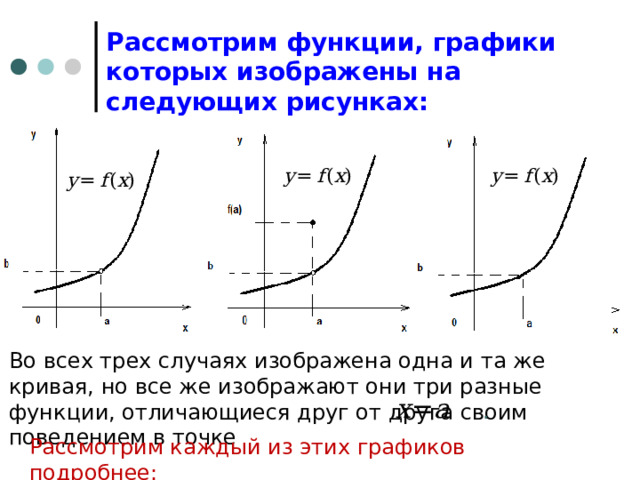
Рассмотрим функции, графики которых изображены на следующих рисунках:

Во всех трех случаях изображена одна и та же кривая, но все же изображают они три разные функции, отличающиеся друг от друга своим поведением в точке

.

Рассмотрим каждый из этих графиков подробнее:

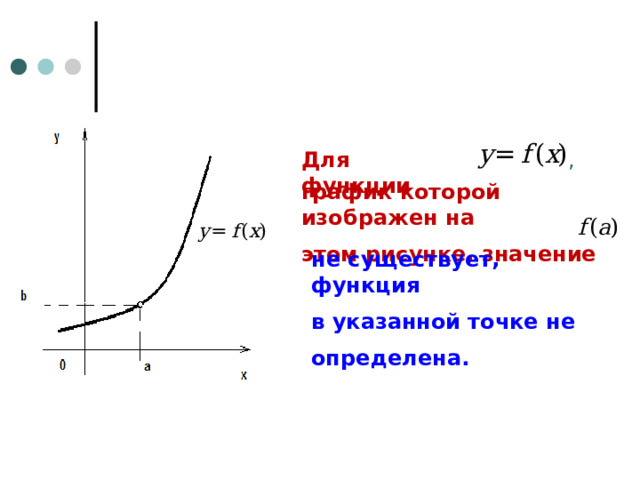
Для функции

,

график которой изображен на

этом рисунке, значение

не существует, функция

в указанной точке не

определена.

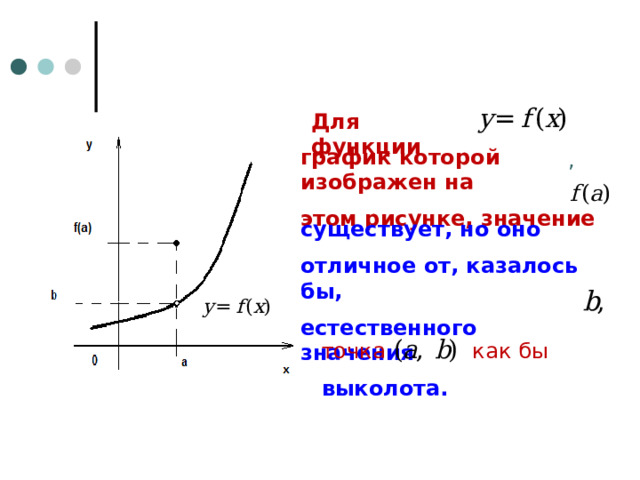
Для функции

график которой изображен на

этом рисунке, значение

,

существует, но оно

отличное от, казалось бы,

естественного значения

точка

как бы

выколота.

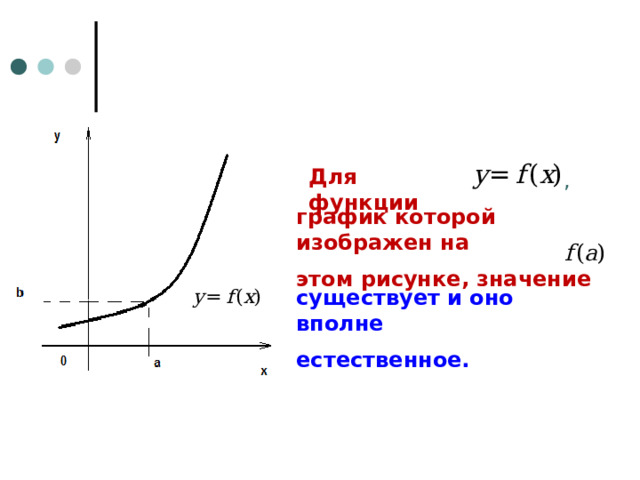
Для функции

,

график которой изображен на

этом рисунке, значение

существует и оно вполне

естественное.

Для всех трех случаев используется одна и та же запись:

при

которую читают: «предел функции

к равен ».

стремлении

Опр. Число называется пределом функции в точке а , если для всех значений х , достаточно близких к а и отличных от а , значение функции

f (x) сколь угодно мало отличается

от .

Теорема 1.

Предел суммы (разности) 2-х функций равен сумме (разности) их пределов, если последние существуют:

Теорема 2.

Предел константы равен самой этой константе.

Теорема 3.

Предел произведения 2-х функций равен произведению их пределов, если последние существуют:

Теорема 4.

Предел отношения 2-х функций равен отношению их пределов, если последние существуют и предел знаменателя отличен от 0 :

Теорема 5.

Постоянный множитель можно выносить за знак предела

Теорема 6.

Предел степени переменного равен той же степени предела основания:

Вычисление пределов

Вычисление предела :

начинают с подстановки предельного значения x 0 в функцию f(x).

Если при этом получается конечное число, то предел равен этому числу.

Если при подстановки предельного значения x 0 в функцию f(x) получаются выражения вида:

то предел будет равен:

7

3

1

3

1,4

Домой (4 примера):

Часто при подстановке предельного значения x 0 в функцию f(x) получаются выражения следующих видов:

Эти выражения называются неопределенности , а вычисление пределов в этом случае называется раскрытие неопределенности .

Правило № 1

• В большинстве случаев, чтобы раскрыть неопределенность вида , достаточно

числитель и знаменатель дроби разложить на множители, и затем сократить на множитель, приводящий к неопределенности.

Пример №1:

Разложим числитель и знаменатель на множители:

Вернемся к примеру

0

-4

-1,5

Домой (№5,6,7):

06/20/2022

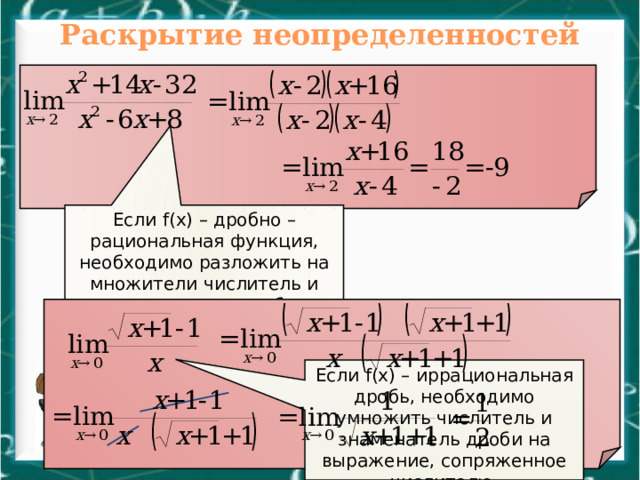
Раскрытие неопределенностей

Если f(x) – дробно – рациональная функция, необходимо разложить на множители числитель и знаменатель дроби

Если f(x) – иррациональная дробь, необходимо умножить числитель и знаменатель дроби на выражение, сопряженное числителю.

Упражнения (13 примеров):

Домашнее задание (№8-11):

+ знать ответы на следующие вопросы:

• С какими математиками связано понятие «Предел»?
• Как вычислить предел?
• Как раскрыть неопределенность вида 0/0?
• Как раскрыть неопределенность вида 0/0, если f(x) – иррациональная дробь?
• Уметь формулировать теоремы.

Дополнительно

06/20/2022