Раздел 11 Элементы теории вероятностей и математической статистики
Лекция № 203 Понятия события и вероятности события. Виды события. Операции над событиями.
Лекция № 204 Классическое определение вероятности.
Основная литература:
-
Уч. пособие “Алгебра. Элементы статистики и теории вероятностей” авторов Ю.Н. Макарычева и Н.Г. Миндюк
-
Математика: учебник / М.И. Башмаков. — Москва : КноРус, 2017.
-
Башмаков М.И. Математика. Задачник: учебное пособие для студ. Учреждений сред проф. образования. - 5-е изд., стер.- М.: Издательский центр «Академия», 2017 год.
-
Математика: учебник для учреждений нач. и сред. проф. образования /М.И. Башмаков.- 7-е изд., стер.- М.: Издательский центр «Академия», 2012 год.
-
http://www.drofa.ru/ (Методические пособия, статьи для обучения математике)
-
http://podgotovka-ege.ru/education/ (Сайт для подготовки к ЕГЭ)
-
https://multiurok.ru/seropol-irina
Мотивация.
В своей практической деятельности мы часто встречаемся с явлениями, исход которых невозможно предсказать, результат которых зависит от случая.
Случайное явление можно охарактеризовать отношением числа его наступления к числу испытаний, в каждом из которых при одинаковых условиях всех испытаний оно могло наступить или не наступить.
Теория вероятности - раздел математики, в котором изучаются случайные явления (события) и выявляются закономерности при массовом их повторении.
Изучение нового материала.
Основные понятия теории вероятностей
Определение: Всякое действие, явление, наблюдение с несколькими различными исходами, реализуемое при данном комплексе условий, будем называть испытанием.
Пример 1: Многократное подбрасывание монеты, процесс изготовления какой-либо детали и т.д.
Определение: Все то, что может произойти при осуществлении некоторого комплекса условий называется событием.
Пример 2: Выпадение «орла» или «решки» при подбрасывание монеты и т.д.
Определение: Событие, которое может произойти, а может и не произойти в процессе наблюдения или эксперимента, называется случайным.
Пример 3: выпадение "решки" при бросании монеты, выпадение четного числа очков при игре в кости, вероятность выбора черного шара при случайном выборе из набора разноцветных шаров и т.д.
Определение: Все рассматриваемые события будем считать равновозможными, т.е. такие, которые имеют равные возможности произойти.
Пример 4: При бросании кости могут появиться 1 очко, 2, 3, 4, 5 и 6 очков и эти исходы испытания являются равновозможными
События принято обозначать заглавными буквами латинского алфавита: A, B, C, D и т.д.
Виды случайных событий
События называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.
Пример 5: Монета брошена 1 раз. События: А - выпал герб и В - выпала решка несовместные.
Пример 6: Брошена игральная кость. События: А - выпала 1, В - выпала 2, С - выпала 3 несовместные.
Определение: События называют совместными, если появление одного из них не исключает появление других событий в одном и том же испытании.
Пример 7: Брошена игральная кость. События: А - выпала 4, событие В - выпало четное число совместные.
Определение: События называют единственно возможными, если появление в результате испытания одного и только одного из них является достоверным событием.
Пример 8: Стрелок произвел выстрел по цели. События: А - попадание в цель, В - промах единственно возможные в данном испытании.
Определение: События называют равновозможными, если есть основание считать, что ни одно из этих событий не является более возможным, чем другие.
Пример 9: Брошена игральная кость. Равновозможные события: А - выпала 3 и В - выпала 5; или С - выпало четное число и Д - выпало нечетное число очков.
Определение: Совокупность всех единственно возможных событий испытания называют полная группа событий.
Пример 10: Стрелок произвел 2 выстрела.
Полная группа событий: где
Событие - промах;
Событие - одно попадание;
Событие - два попадания;
Определение: Противоположными называют два единственно возможных события образующих полную группу событий. Обозначение: A¯;
Пример 11:Монета брошена 1 раз. События: - выпал герб и - выпала решка противоположные.
Пример 12: Брошена игральная кость. События: - выпало четное число очков и - выпало нечетное число очков противоположные.
События: - выпала 1 и - не выпала 1 противоположные.
Операции над событиями
Определение: Суммой конечного числа событий называют новое событие, состоящее в наступлении хотя бы одного из них. (Суммой событий А и В называют событие состоящее в появлении или события А или события В, или обоих событий.);
Логический принцип: или - или.
Обозначение: А+В
Пример 13: Событие А - попадание в круг, а событие В - попадание в квадрат;
Тогда их сумма А+В заключается в попадании или в круг или в квадрат
Определение: Произведением конечного числа событий называют новое событие, состоящее в том, что произойдут все эти события.
(Произведением двух событий А и В называют событие, состоящее и в появлении события А и в появлении события В).
Логический принцип и - и.
Обозначение: АВ
Пример 14: Событие А - попадание в круг, а событие В - попадание в квадрат;
Тогда их произведение АВ заключается в попадании в общую часть круга и квадрата.
Относительная частота событий
Зарождение теории вероятностей произошло в поисках ответа на вопрос: как часто наступает то или иное событие в большой серии испытаний со случайными исходами, которые происходят в одинаковых условиях?
Рассмотрим такой пример. Бросают игральный кубик, т. е. небольшой куб, на гранях которого выбиты очки 1, 2, 3, 4, 5, 6 (рис. 13). При бросании игрального кубика на его верхней грани может выпасть одно очко, два очка, три очка и т. д. Каждый из этих исходов является случайным.
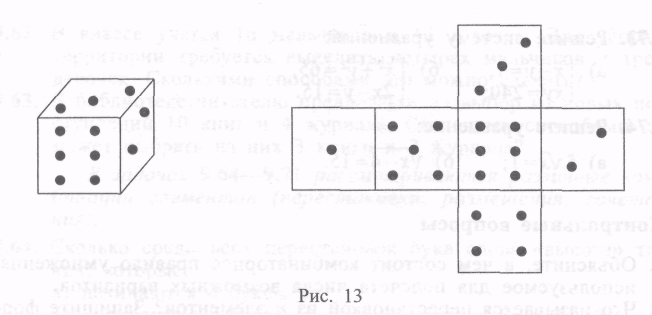
Провели такое испытание. Игральный кубик бросали 100 раз и наблюдали, сколько раз произойдет событие «на кубике выпало 6 очков». Оказалось, что в данной серии экспериментов «шестерка» выпала 9 раз. Число 9, которое показывает, сколько раз в этом испытании произошло рассматриваемое событие, называют частотой этого события, а отношение частоты к общему числу испытании, равное 0,09, называют относительной частотой этого события.
Вообще, пусть определенное испытание проводится многократно в одних и тех же условиях и при этом каждый раз фиксируется, произошло или нет интересующее нас событие А. Обозначим буквой п общее число испытаний, а буквой т число испытаний, при которых произошло событие А.
Определение: Относительной частотой случайного события в серии испытаний называется отношение числа испытаний, в которых это событие наступило, к числу всех испытаний, т.е. 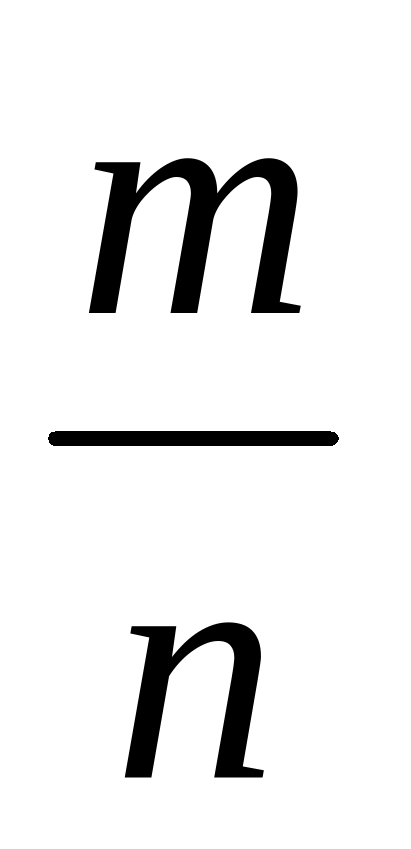 .
.
В ходе статистических исследований установлено, что при многократном повторении отдельных опытов или наблюдений в одних и тех же условиях относительная частота появления ожидаемого события остается примерно одинаковой, незначительно отличаясь от некоторого числа р. Например, при бросании монеты она может упасть кверху орлом или решкой. Если монета однородна и имеет правильную геометрическую форму, то шансы выпадения орла или решки одинаковы. При небольшом числе испытаний выпадение орла может, например, произойти чаще, чем решки. Однако если эти испытания проводятся достаточно большое число раз, то относительная частота выпадения орла близка к относительной частоте выпадения решки.
Классическое определение вероятности
Многие исследователи проводили испытания с бросанием монеты и вычисляли относительную частоту выпадения орла. В таблице указано число бросков монеты в проводимых ими испытаниях и относительные частоты выпадения орла.
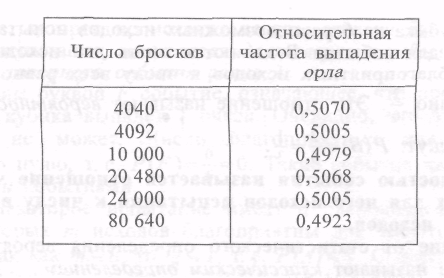
Из таблицы видно, что относительная частота выпадения орла незначительно отличается от 0,5. Говорят, что вероятность выпадения орла близка к 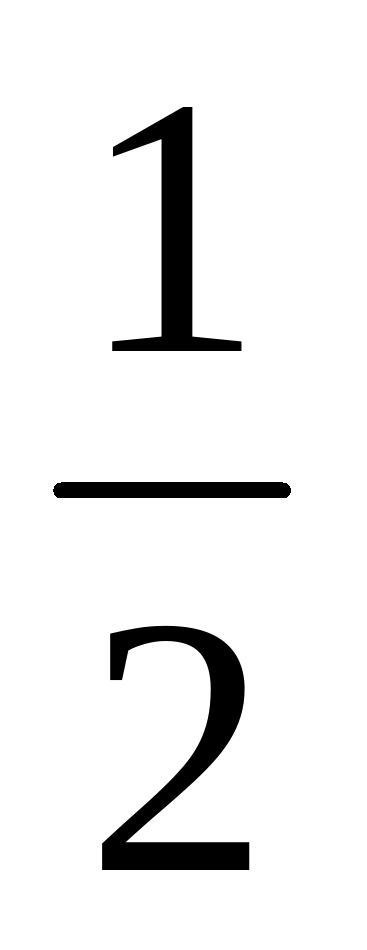 .
.
Вообще, если в длинной серии экспериментов со случайными исходами значения относительных частот близки к некоторому определенному числу, то это число принимают за вероятность данного случайного события. Такое определение называют статистическим определением вероятности.
Вероятность случайного события находят, когда в ходе статистического исследования анализируют относительную частоту наступления этого события при многократном повторении в одних и тех же условиях эксперимента или наблюдения. Так, например, поступают, когда хотят определить ожидаемую всхожесть семян некоторого растения, предсказать результат выступления спортсмена в соревнованиях по стрельбе и т. п.
Для того чтобы найти вероятность интересующего нас события, необходимо предварительно провести достаточно большое число экспериментов или наблюдений. В то же время если рассматриваются испытания со случайными исходами и все исходы этих испытаний равновозможны, т. е. имеются основания считать, что шансы их наступления одинаковы, то вероятность наступления случайного события удается найти путем рассуждений, не прибегая к испытанию.
Вернемся к рассмотренному примеру с бросанием игрального кубика. Будем считать, что этот кубик имеет правильную форму и сделан из однородного материала и поэтому при его бросании шансы выпадения на его верхней грани любого числа очков от 1 до 6 одинаковы. Говорят, что существует шесть равновозможных исходов этого испытания: выпадение очков 1, 2, 3, 4, 5 и 6.
Рассмотрим событие В, которое означает выпадение числа очков, кратного 3. Это событие происходит лишь при двух исходах испытания: когда выпало 3 очка и когда выпало 6 очков. Эти исходы называют благоприятными исходами для события В. При бросании кубика из 6 равновозможных исходов испытания благоприятными для события В являются лишь два исхода. Отношение числа благоприятных исходов к числу всех равновозможных исходов равно 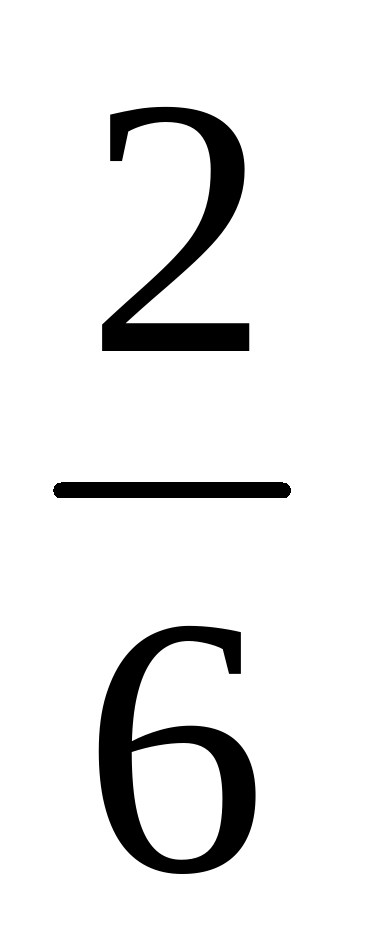 . Это отношение называют вероятностью события В и пишут: Р(В) =
. Это отношение называют вероятностью события В и пишут: Р(В) =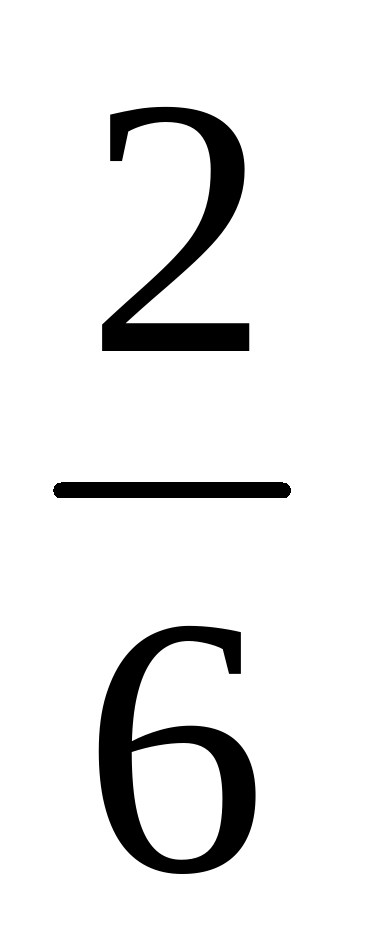 =
= .
.
Определение: Вероятностью события A называется отношение числа m благоприятных для него исходов испытания к числу n всех равновозможных исходов, т.е.
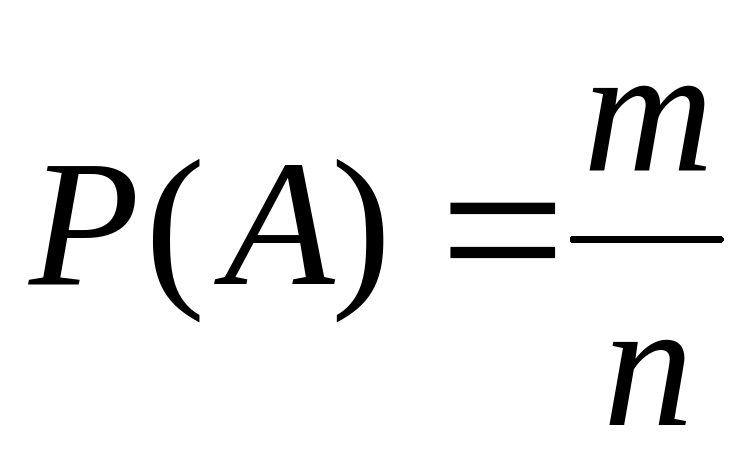
В отличие от статистического определения вероятности это определение называют классическим определением.
Что означает на практике, что вероятность рассмотренного события В равна 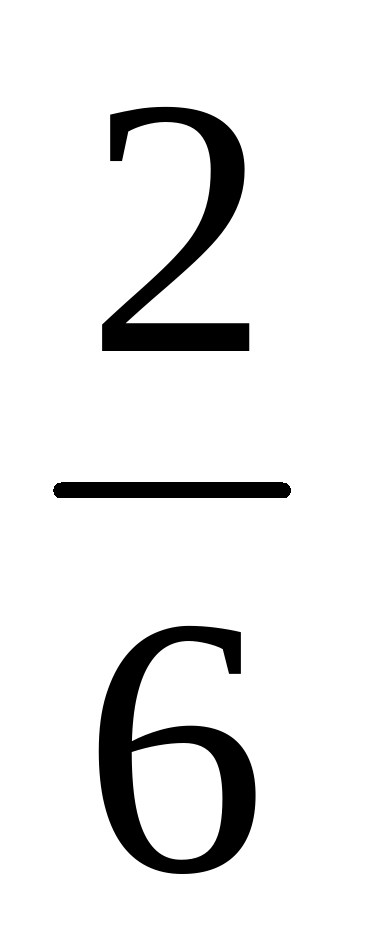 ? Разумеется, это не означает, что при шести бросках число очков, кратное 3, выпадает ровно два раза. Возможно, что оно выпадает один раз, три раза или не выпадет совсем. Однако если провести большое число испытаний, то относительная частота появления события В будет мало отличаться от
? Разумеется, это не означает, что при шести бросках число очков, кратное 3, выпадает ровно два раза. Возможно, что оно выпадает один раз, три раза или не выпадет совсем. Однако если провести большое число испытаний, то относительная частота появления события В будет мало отличаться от 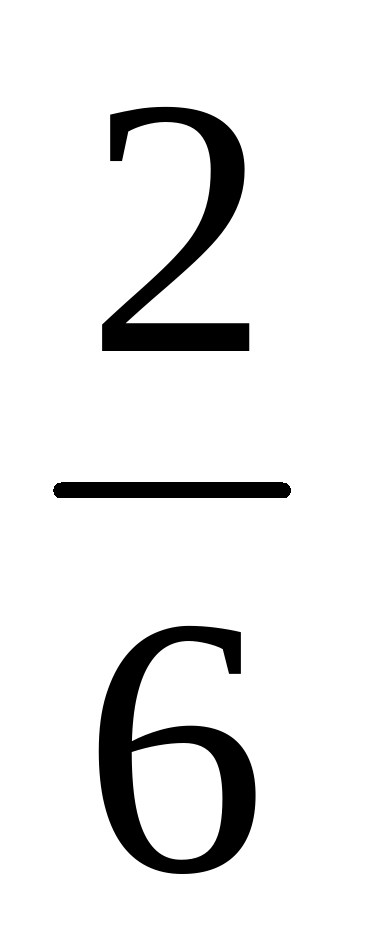 . Вообще, при увеличении числа испытаний относительная частота появления случайного события приближается к его вероятности.
. Вообще, при увеличении числа испытаний относительная частота появления случайного события приближается к его вероятности.
Сопоставляя классическое и статистическое определения вероятности, можно сделать вывод, что нахождение классической вероятности не требует, чтобы испытание было проведено в действительности, а нахождение статистической вероятности (относительной частоты) предполагает фактическое проведение испытания.
Для того чтобы найти вероятность некоторого события, надо правильно определить число равновозможных исходов испытания и число благоприятных для этого события исходов.
Рассмотрим, например, известную задачу Даламбера (1717— 1783): «Найти вероятность того, что при подбрасывании двух монет на обеих монетах выпадут решки».
При бросании монет равновозможными являются следующие исходы: (о;о), (о;р), (р;р), (р;о), где в каждой паре на первом месте записан результат бросания первой монеты, а на втором — результат бросания второй монеты, причем выпадение орла обозначено буквой о, а выпадение решки — буквой р.
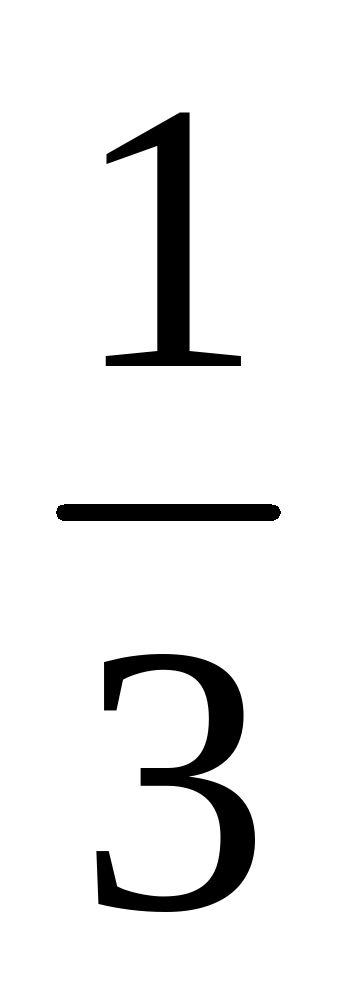
Благоприятным для события А, состоящего в том, что оба раза выпадут решки, является один исход. Значит, P(А)=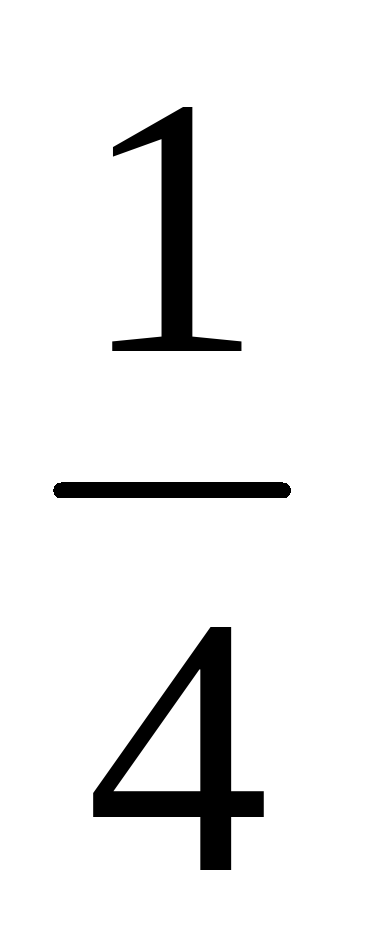 .
.
Введем теперь понятия достоверного и невозможного события.
Пусть С-событие, состоящее в том, что при бросании игрального кубика выпадет менее 7 очков. Так как каждый из исходов 1, 2, 3, 4, 5, 6 является благоприятным для события С, то вероятность наступления события С равна: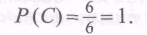
Определение: Если при реализации условий событие происходит всегда, то оно называется достоверным. Вероятность достоверного события равна 1.
Например: выпадение на игральной кости натурального числа меньшего 7, после понедельника всегда наступает вторник и т.д.
Обозначим буквой F событие, означающее, что при бросании игрального кубика выпадет 7 очков. Очевидно, что это событие произойти не может. Число благоприятных для него исходов равно нулю, т. е. P(F) =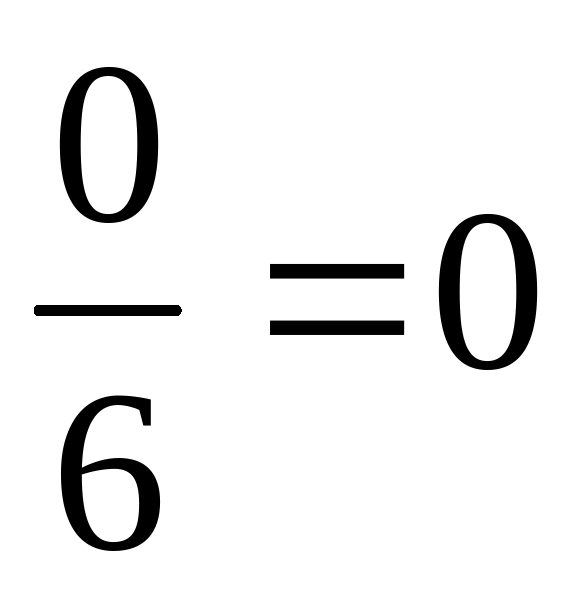 . Такие события называют невозможными событиями.
. Такие события называют невозможными событиями.
Определение: Если событие при заданных условиях никогда не наступает, то его называют невозможным
Например: выпадение 7 очков при выбрасывании игральной кости, наступление после июня августа и т.д.
Пусть некоторое испытание имеет п равновозможных исходов, из которых т исходов благоприятны для события А. Тогда 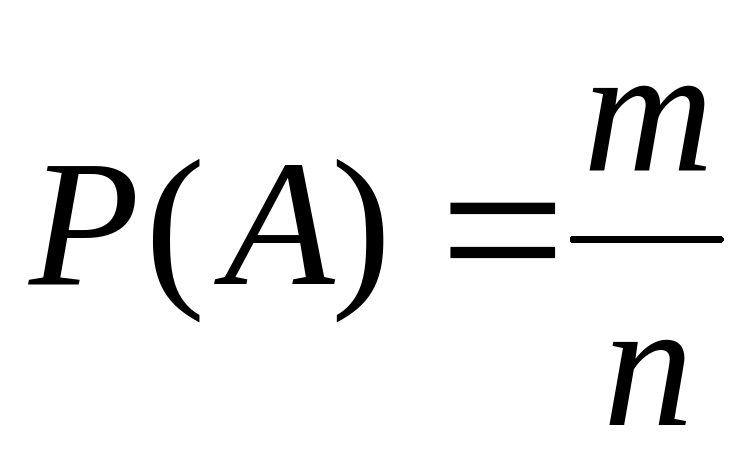 . Так как тто
. Так как тто 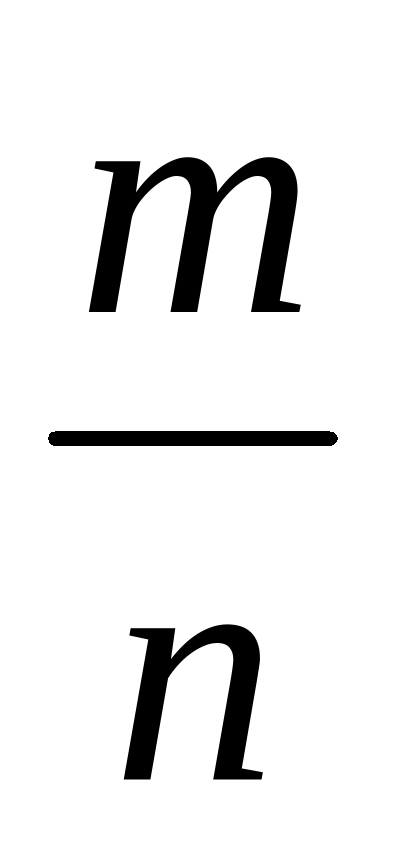 Р(A) 1. С другой стороны, всегда Р(А)0. Следовательно, 0P(A)1.
Р(A) 1. С другой стороны, всегда Р(А)0. Следовательно, 0P(A)1.
Свойства вероятности события.
-
Вероятность любого события есть неотрицательное число, не превосходящее единицы, т.е. 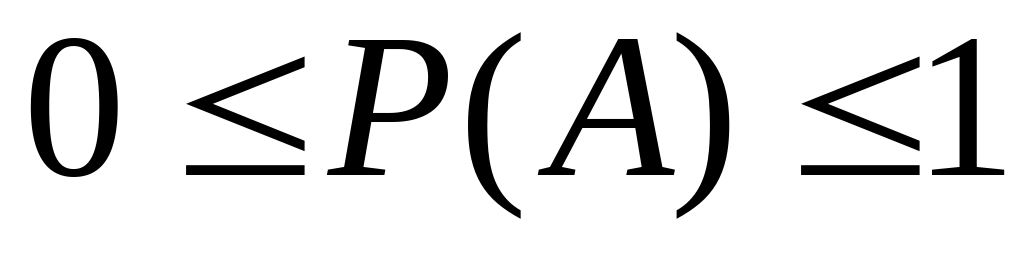 .
.
-
Вероятность достоверного события равна единице, т.к. 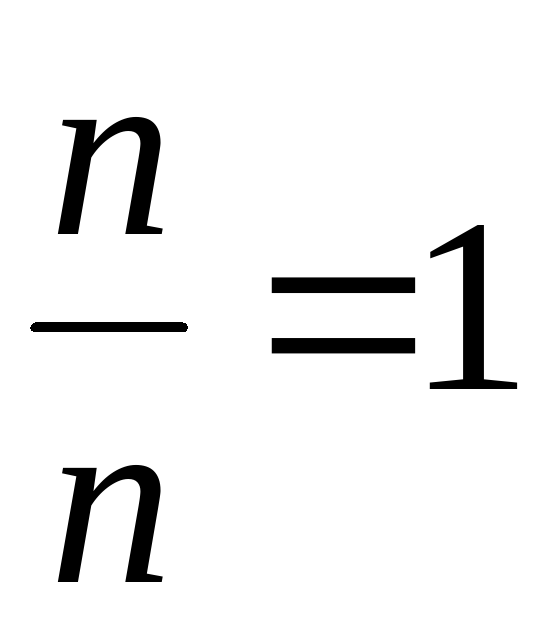 .
.
-
Вероятность невозможного события равна нулю, т.к. 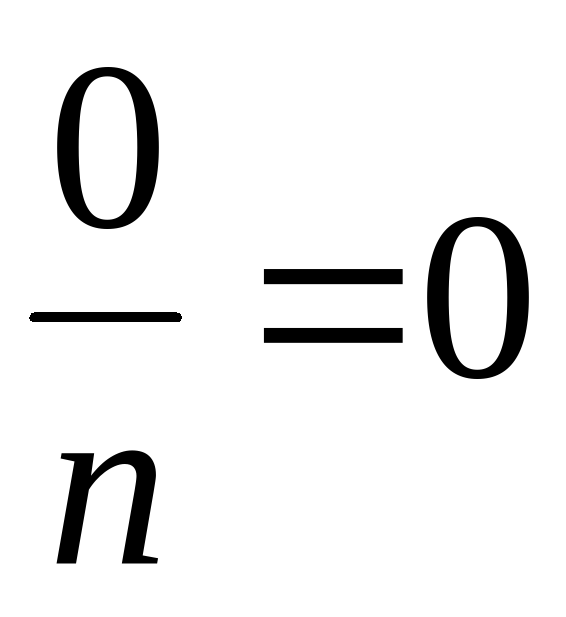 .
.
Задача 1. Из 25 экзаменационных билетов по геометрии ученик успел подготовить 11 первых и 8 последних билетов. Какова вероятность того, что на экзамене ему достанется билет, который он не подготовил?
Решение: Общее число равновозможных исходов при выборе билетов на экзамене 25. Пусть М—событие, заключающееся в том, что ученику достанется на экзамене билет, к которому он не подготовился. Число благоприятных для события М исходов (но не для ученика) равно 25-(11 + 8), т. е. 6. Значит,
Р(М) =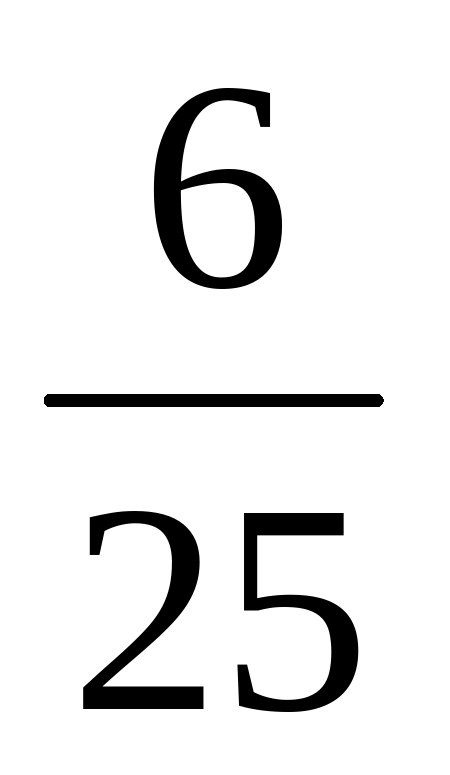 = 0,24.
= 0,24.
Задача 2. Антон и Игорь бросают белый и черный игральные кубики и подсчитывают сумму выпавших очков. Они договорились, что если при очередной попытке в сумме выпадет 8 очков, то выигрывает Антон, а если в сумме выпадет 7 очков, то выигрывает Игорь. Является ли такая игра справедливой?
Решение: При бросании кубиков на белом кубике может выпасть 1, 2, 3, 4, 5 или 6 очков. Каждому числу очков, выпавших на белом кубике, соответствует шесть вариантов числа очков, выпавших на черном кубике. Все равновозможные исходы этого испытания приведены в таблице:
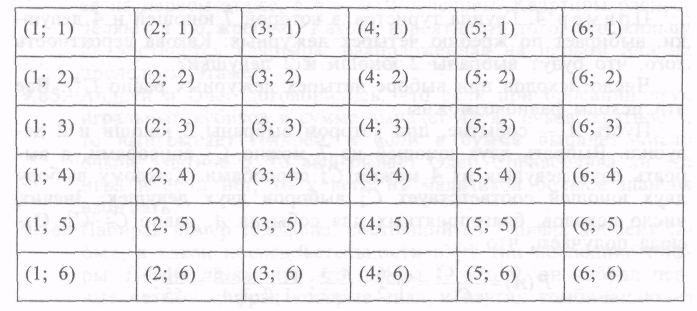
В каждой паре на первом месте записано число очков, выпавших на белом кубике, а на втором месте — число очков, выпавших на черном кубике. Общее число равновозможных исходов равно 36.
Пусть событие А означает, что при бросании кубиков в сумме выпало 8 очков, а событие В означает, что в сумме выпало 7 очков.
Для события А благоприятными являются следующие 5 исходов:
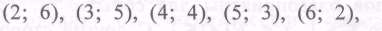
Для события В благоприятными являются следующие 6 исходов:
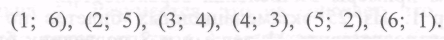
Отсюда: 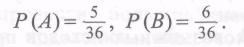
Поэтому шансов выиграть у Игоря больше, чем у Антона. Значит, такая игра не является справедливой.
Задача 3. Из 16 собранных велосипедов 4 оказались с дефектами. Какова вероятность того, что 2 выбранных наугад велосипеда будут без дефектов?
Решение: Пусть А — событие, при котором 2 выбранных велосипеда окажутся без дефектов. Любой выбор 2 велосипедов из 16, является равновозможным исходом. Значит, общее число равновозможных исходов равно числу сочетаний из 16 по 2, т.е.  . Исходом, благоприятным для события А, является выбор 2 исправных велосипедов из имеющихся 12 исправных (16-4 = 12). Значит, число благоприятных для события А исходов равно
. Исходом, благоприятным для события А, является выбор 2 исправных велосипедов из имеющихся 12 исправных (16-4 = 12). Значит, число благоприятных для события А исходов равно  . Отсюда получаем, что
. Отсюда получаем, что
Задача 4. Группа туристов, в которой 7 юношей и 4 девушки, выбирает по жребию четырех дежурных. Какова вероятность того, что будут выбраны 2 юноши и 2 девушки?
Решение: Число исходов при выборе четырех дежурных равно . Все эти исходы равновозможны.
Пусть А - событие, при котором выбраны 2 юноши и 2 девушки. Выбрать двух юношей из 7 можно , способами, а выбрать двух девушек из 4 можно способами. Каждому выбору двух юношей соответствует выборов двух девушек. Значит, число исходов, благоприятных для события А, равно . Отсюда получаем, что
ЗАДАЧИ, ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.
-
В партии из 1000 деталей отдел технического контроля обнаружил 12 нестандартных деталей. Какова относительная частота появления нестандартных деталей?
-
Выберите какой-нибудь текст, содержащий 150 слов. Подсчитайте число слов, составленных из шести букв. Найдите относительную частоту появления слов, которые составлены из шести букв.
-
Выберите 7 строк произвольного текста. Проведя подсчет букв, найдите относительную частоту появления буквы:
-
а) о; б) е; в) а; г) ю.
-
Проделайте дома такой опыт: подбросьте 50 раз монету в 1 р. и подсчитайте, сколько раз выпадет орел. Запишите результаты в тетради. В классе подсчитайте, сколько всеми учениками было проведено опытов и каково общее число выпадений орла. Вычислите относительную частоту выпадения орла при бросании монеты.
-
На учениях по стрельбе из винтовки относительная частота поражения цели у некоторого стрелка оказалась равной 0,8. Сколько попаданий в цель можно ожидать от этого стрелка на соревнованиях, если каждый участник произведет по 20 выстрелов?
-
Многократная проверка показала, что всхожесть семян огурцов определенного сорта равна 0,9. Посадили 85 семян этого сорта. Найдите ожидаемое число проросших семян.
-
Для новогодней лотереи отпечатали 1500 билетов, из которых 120 выигрышных. Какова вероятность того, что купленный билет окажется выигрышным?
ДОМАШНЕЕ ЗАДАНИЕ.
Лекция № 203
Выполнить конспект из Лекция №203 или учебника [1], гл.11, с.217-218
Решить задачи Задачник [2], с.266, №11.12, 11.13, 11.17
Лекция № 204
Выполнить конспект из Лекция №204 или учебника [1], гл.11, с.217-218
Решить задачи Задачник [2], с.267, №11.19 - 11.21


























