

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Был в сети 12.05.2024 20:45

Федорченко Александр Сергеевич
преподаватель
27 лет
Местоположение
Россия, Нефтекумск
Специализация
Лекция "Определение производной. Дифференцируемость функции. Правила дифференцирования. Производные основных функций. Производная сложной функции"
Категория:
Математика
07.04.2024 13:15


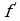 (x0).
(x0). 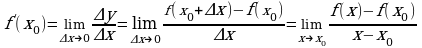

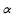
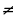 0, то их частное дифференцируемо в этой точке, причем:
0, то их частное дифференцируемо в этой точке, причем: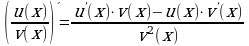
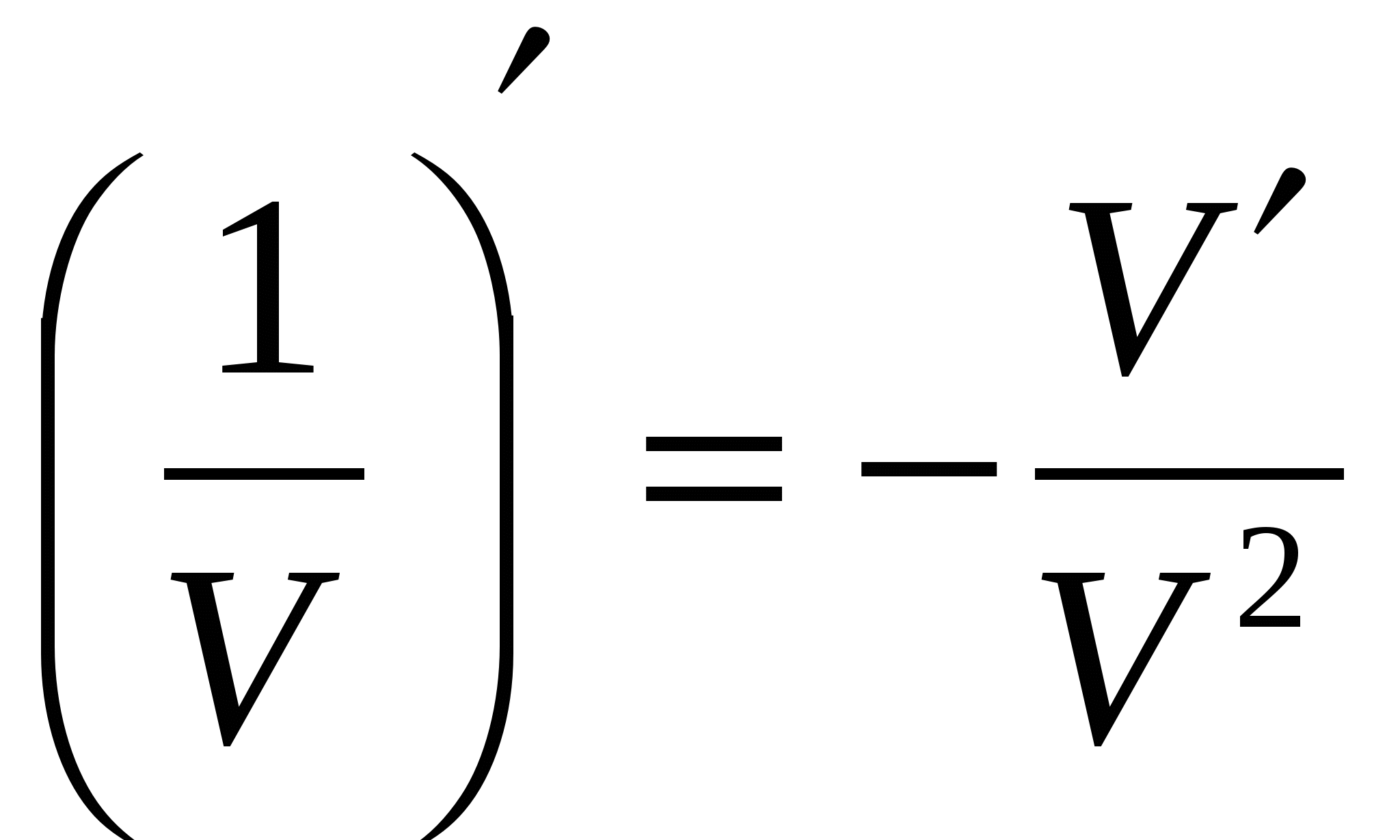 1)
1) 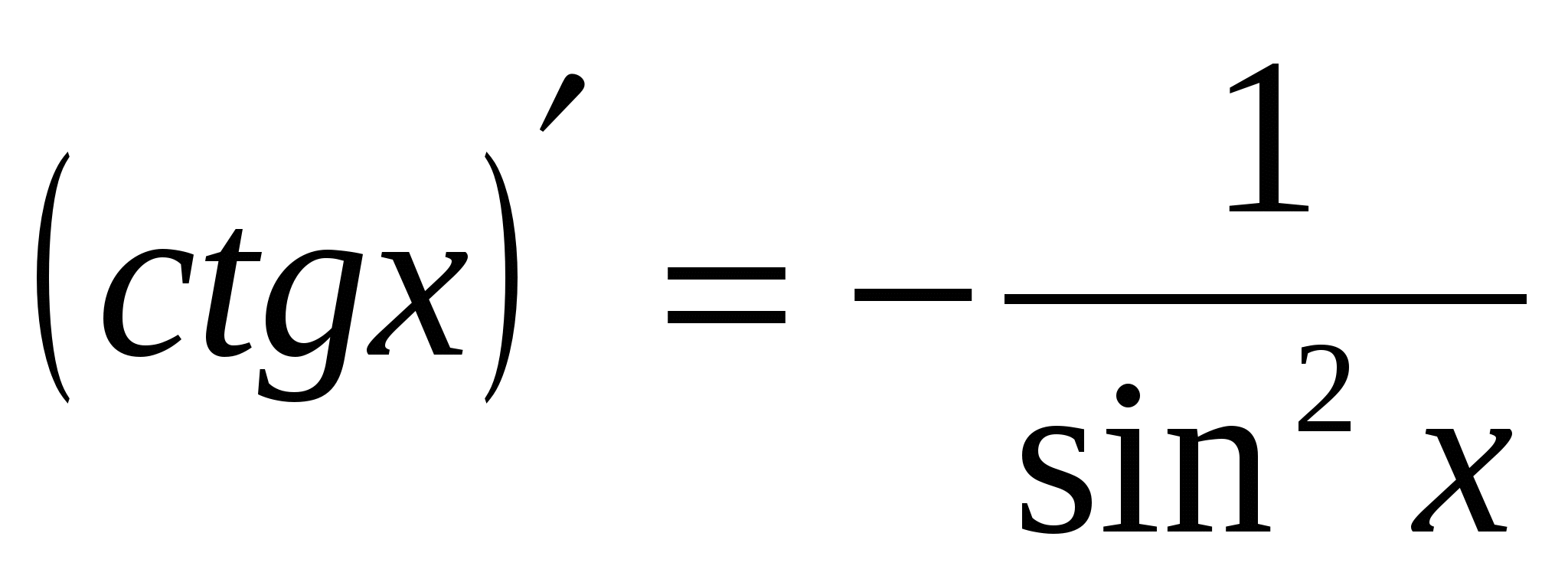
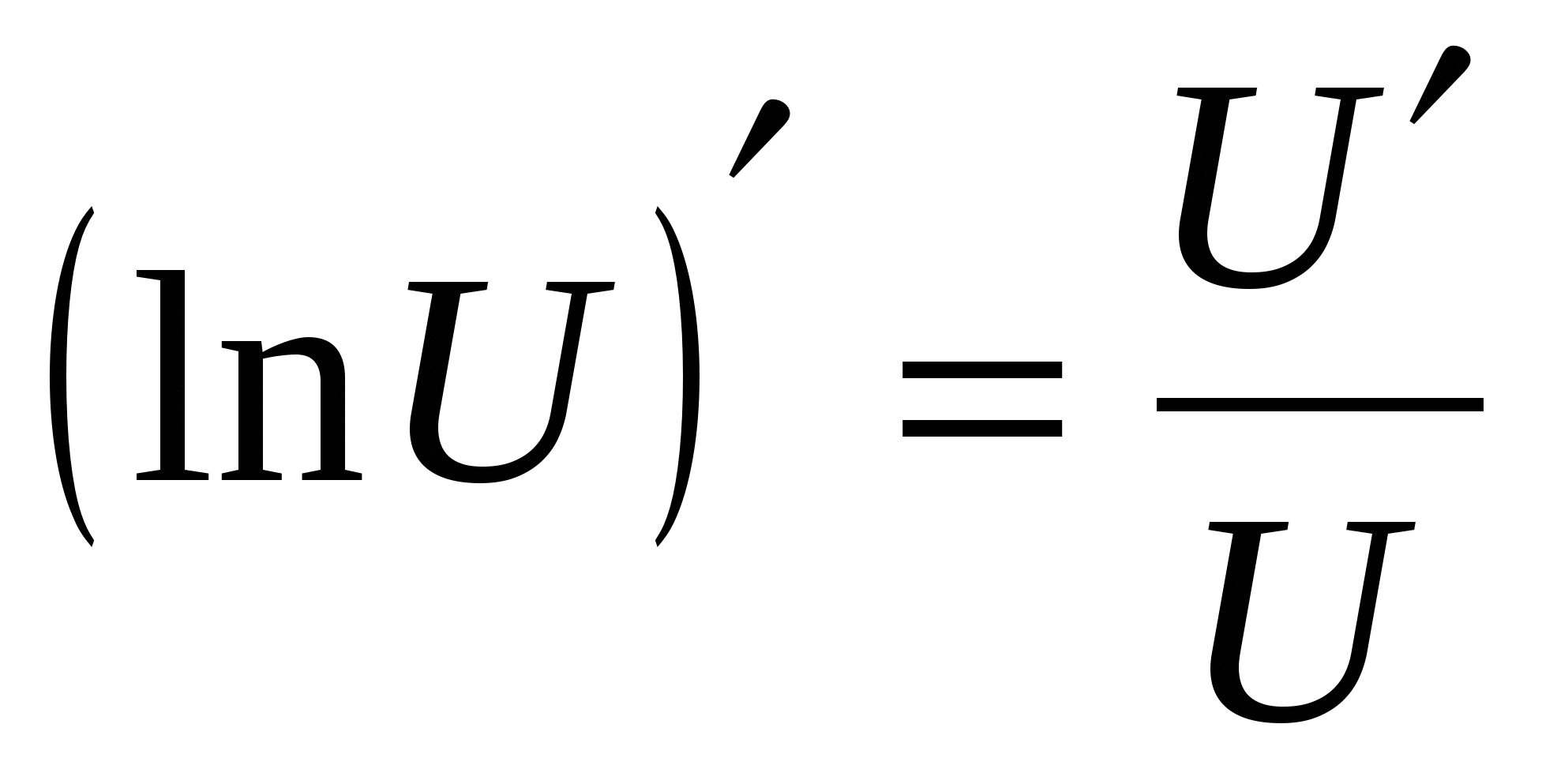 10
10 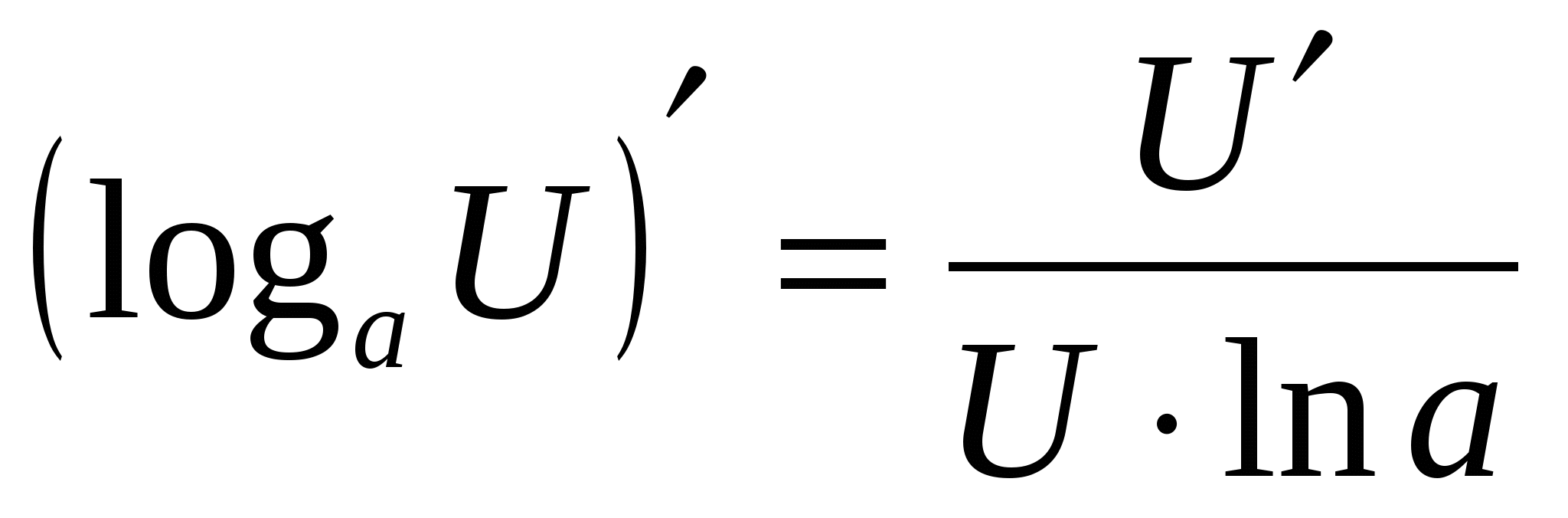 11
11

















