Предел функции в точке. Основные теоремы о пределах. Бесконечно малые и бесконечно большие функции. Некоторые замечательные пределы. Непрерывность функции и ее разрывы.
Пусть функция y =f(x) определена в некоторойокрестностиx0,кроме, может быть, самой точки x0.
Определение. Число A называется пределом функции y =f(x) в точке x0 (или при х →x0), если для любого сколь угодно малого числа ε 0 найдется такое число δ 0, что для всех х ¹x0, удовлетворяющих неравенству
│ х –x0│f(x) –А│
Или кратко: 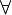 ε 0
ε 0  δ 0,
δ 0, 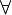 x:│ х –x0│х ¹x0= │f(x) –А│
x:│ х –x0│х ¹x0= │f(x) –А│
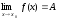
Геометрический смысл предела функции заключается в следующем: число 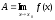 , если для любой ε – окрестности точки A найдется такая δ – окрестность точки x0, что для всех х ¹x0 из этой окрестности соответствующие значения функции f(x) лежат в ε – окрестности точки А.
, если для любой ε – окрестности точки A найдется такая δ – окрестность точки x0, что для всех х ¹x0 из этой окрестности соответствующие значения функции f(x) лежат в ε – окрестности точки А.
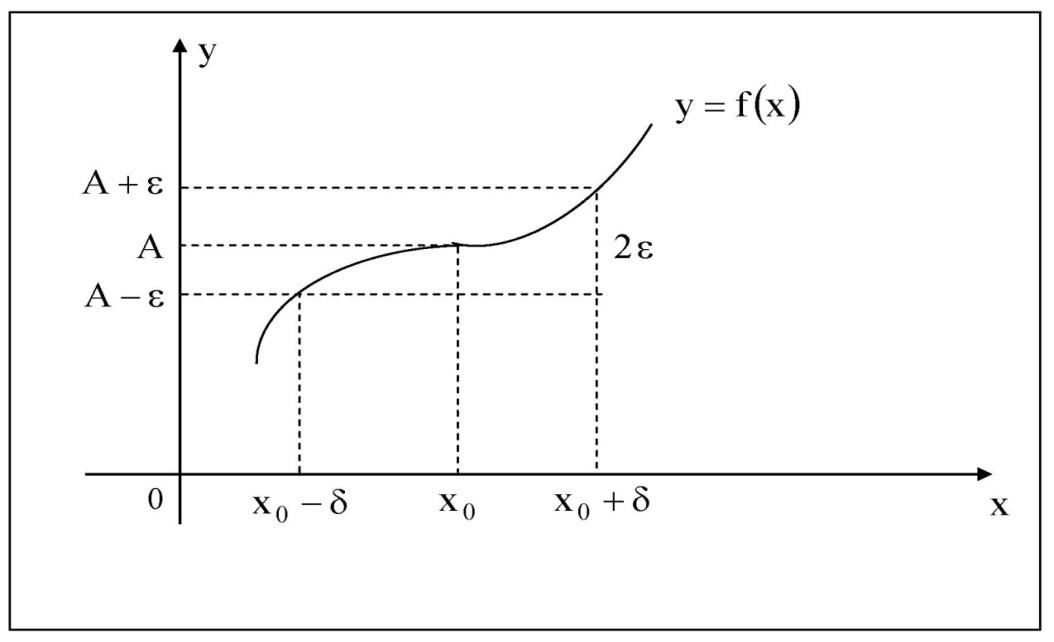
Рис. 1
Пример: Доказать, что 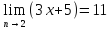
Решение. Возьмем произвольное 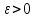 и найдем
и найдем 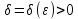 такое, что для всехx, удовлетворяющих неравенству,
такое, что для всехx, удовлетворяющих неравенству, 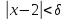 , выполняется неравенство
, выполняется неравенство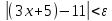 , то есть
, то есть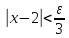 .
.
Взяв 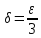 , видим, что для всехx, удовлетворяющих неравенству,
, видим, что для всехx, удовлетворяющих неравенству, 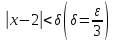 , выполняется неравенство
, выполняется неравенство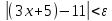 , следовательно,
, следовательно,
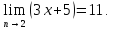
Пусть функция y =f(x) определена в промежутке (– ; +
; + ).
).
Определение. Число A называется пределом функции f(x) при х 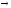
 , если для любого числа ε 0 существует такоечисло M = M (ε) 0, что для всех значений x, удовлетворяющих неравенству │x│M,выполняется неравенство │f(x) – А│ ε. В этом случае пишут
, если для любого числа ε 0 существует такоечисло M = M (ε) 0, что для всех значений x, удовлетворяющих неравенству │x│M,выполняется неравенство │f(x) – А│ ε. В этом случае пишут 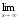 f(x) = А.
f(x) = А.
Или кратко: 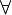 ε 0
ε 0  M 0, │x│ M= │f(x) –А│
M 0, │x│ M= │f(x) –А│
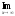 f(x) = А.
f(x) = А.
Бесконечно малые и бесконечно большие функции.
Определение 1. Функция f(x) называется бесконечно большой функцией при х →x0, если 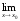 f(x) =
f(x) =  .
.
Определение 2. Функция f(x) называется бесконечно малой функцией при х →x0, если 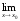 f(x) = 0.
f(x) = 0.
Основные теоремы о пределах функций.
Теорема 1. Предел постоянной величины равен самой постоянной: 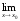 c = c.
c = c.
Теорема 2. Предел суммы (разности) двух функций равен сумме (разности) их пределов: 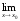
 =
= 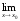 f(x)
f(x)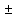
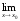 φ(x).
φ(x).
Теорема 3.Предел произведения двух функций равен произведению их пределов:
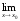
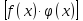 =
= 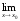 f(x)
f(x)
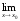 φ(x).
φ(x).
Теорема 4. Предел дроби равен пределу числителя, деленному на передел знаменателя, если предел знаменателя не равен нулю:
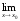
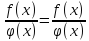 ,
, 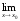
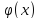 0.¹
0.¹
Теорема 5. (О пределе промежуточной функции) Если в окрестности точки x0 выполняются неравенства: 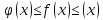 и
и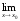
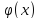 =
=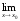
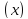 =А, то
=А, то 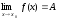 .
.
Первый замечательный предел 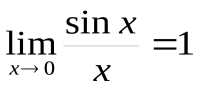 .
.
Второй замечательный предел.
Функция 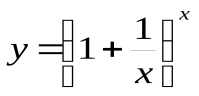 при
при и
и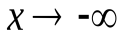 (где х в отличие от натурального n «пробегает» все значения числовой оси) имеет предел, равный числу е:
(где х в отличие от натурального n «пробегает» все значения числовой оси) имеет предел, равный числу е:
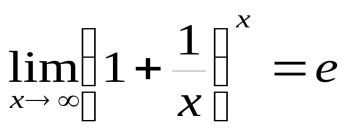 .
.
Эквивалентные бесконечно малые функции используются при вычислении пределов отношений двух бесконечно малых для раскрытия неопределенностей вида 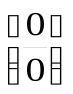 .
.
Запишем следствия из 1-го и 2-го замечательных пределов в виде таблицы эквивалентных бесконечно малых. При 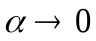
Пример. 1) Найти 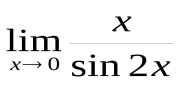 .
.
При 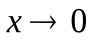
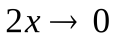 и, значит,
и, значит,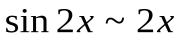 . Заменяя знаменатель на эквивалентную бесконечно малую, получаем
. Заменяя знаменатель на эквивалентную бесконечно малую, получаем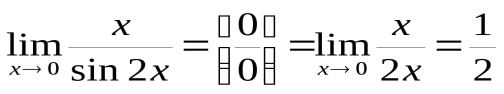 .
.
2) Найти 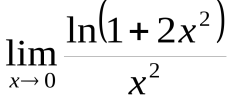 .
.
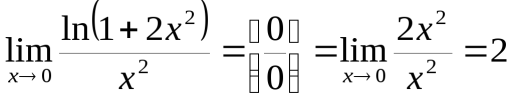 .
.
3) Найти 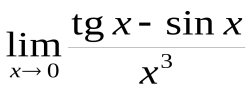 .
.
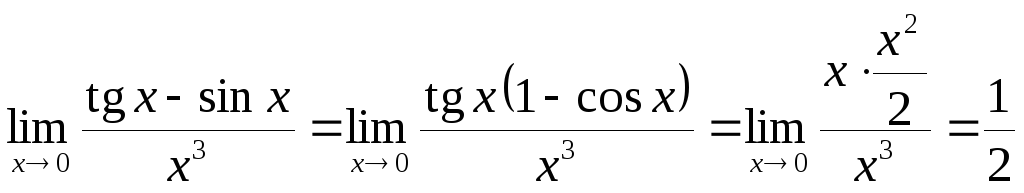
Определение 1. Функция 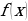 , определенная в некоторой окрестности точки
, определенная в некоторой окрестности точки 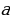 , называется непрерывной в точке
, называется непрерывной в точке 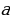 , если
, если 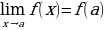 .
.
Необходимо обратить внимание учащихся на то, что согласно данному определению непрерывность функции 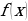 в точке
в точке 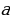 означает одновременную выполняемость следующих условий:
означает одновременную выполняемость следующих условий:
1. Функция 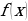 должна быть определена в точке
должна быть определена в точке 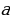 .
.
2. У функции 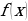 должен существовать предел в точке
должен существовать предел в точке 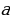 . Как отмечалось выше, это подразумевает существование и равенство односторонних пределов в точке
. Как отмечалось выше, это подразумевает существование и равенство односторонних пределов в точке 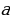 .
.
3. Предел функции 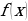 в точке
в точке 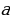 совпадает со значением функции в этой точке.
совпадает со значением функции в этой точке.
Определение 2. Функция называется непрерывной в точке 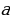 , если бесконечно малому приращению аргумента
, если бесконечно малому приращению аргумента 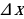 соответствует бесконечно малое приращение функции
соответствует бесконечно малое приращение функции 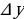 , то есть
, то есть 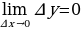 .
.
Определение 3. Если функция 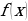 определена на полуинтервале
определена на полуинтервале  и
и 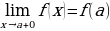 , т.е.
, т.е. 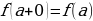 , то эта функция называется непрерывной справа в точке
, то эта функция называется непрерывной справа в точке 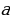 .
.
Определение 4. Если функция 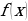 определена на полуинтервале
определена на полуинтервале  и
и 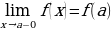 , т.е.
, т.е. 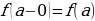 , то эта функция называется непрерывной слева в точке
, то эта функция называется непрерывной слева в точке 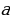 .
.
Для непрерывности функции в точке необходимо и достаточно её непрерывности в этой точке слева и справа.
Определение 5. Если функция непрерывна в каждой точке интервала 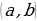 , то она называется непрерывной на этом интервале.
, то она называется непрерывной на этом интервале.
Определение 6. Функция называется непрерывной на отрезке 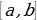 , если она непрерывна на интервале
, если она непрерывна на интервале 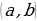 и, кроме того, непрерывна справа в точке
и, кроме того, непрерывна справа в точке 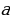 и непрерывна слева в точке
и непрерывна слева в точке 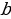 .
.
Определение 7. Точка 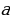 называется точкой разрыва функции
называется точкой разрыва функции 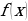 , если эта функция либо не определена в точке
, если эта функция либо не определена в точке 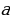 , либо определена, но не является непрерывной в точке
, либо определена, но не является непрерывной в точке 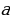 .
.
При этом следует отметить, что в точке разрыва нарушается одно из трех условий непрерывности. В зависимости от того, какое условие нарушается, выделяют точки разрыва первого рода (точки устранимого разрыва, точки разрыва с конечным скачком функции) и точки разрыва второго рода. У каждого типа разрыва есть свои характерные особенности, на которые нужно обратить внимание.
Определение. Точка х0 называется точкой разрыва 1 - го рода, если в этой точке функция 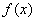 имеет конечные, но не равные друг другу левый и правый пределы.
имеет конечные, но не равные друг другу левый и правый пределы. 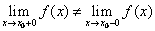
Для выполнения условий этого определения не требуется, чтобы функция была определена в точке 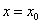 , достаточно того, что она определена слева и справа от нее.
, достаточно того, что она определена слева и справа от нее.
Из определения можно сделать вывод, что в точке разрыва 1 - го рода функция может иметь только конечный скачок.
Определение. Точка х0 называется точкой разрыва 2 - го рода, если в этой точке функция 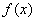 не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.
не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.
Пример. Функция Дирихле (Дирихле Петер Густав(1805-1859) - немецкий математик, член-корреспондент Петербургской АН 1837г)
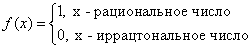
не является непрерывной в любой точке 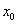 .
.
Пример. Функция  имеет в точке
имеет в точке 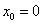 точку разрыва 2 - го рода, т.к.
точку разрыва 2 - го рода, т.к. 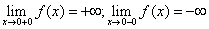 .
.
Основные свойства функции, непрерывной в точке:
1. Ограниченность в некоторой окрестности точки 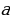 непрерывной в точке
непрерывной в точке 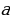 функции.
функции.
2. Знак функции, непрерывной в точке 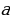 , в некоторой окрестности этой точки.
, в некоторой окрестности этой точки.
3. Непрерывность в точке суммы, произведения и частного непрерывных в точке функций.
4. Непрерывность сложной функции.
Формулировка основных свойств функций, непрерывных на отрезке
1. Теорема о нулях непрерывной на отрезке функции.
Если функция 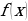 определена и непрерывна на отрезке
определена и непрерывна на отрезке 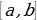 и принимает на его концах значения разных знаков, т.е.
и принимает на его концах значения разных знаков, т.е. 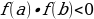 , то на интервале
, то на интервале 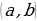 имеется по крайней мере один корень функции, т.е.
имеется по крайней мере один корень функции, т.е. 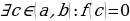 .
.
2. Теорема о промежуточных значениях непрерывной на отрезке функции.
Если функция 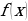 определена и непрерывна на отрезке
определена и непрерывна на отрезке 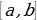 и принимает на его концах различные значения
и принимает на его концах различные значения 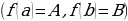 , то для любого числа C, лежащего между A и B, на интервале
, то для любого числа C, лежащего между A и B, на интервале 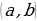 найдется такая точка с, что
найдется такая точка с, что 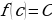 .
.
3. Теорема об ограниченности непрерывной на отрезке функции.
Если функция 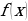 непрерывна на отрезке
непрерывна на отрезке 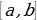 , то она ограничена на этом отрезке.
, то она ограничена на этом отрезке.
4. Теорема о достижимости своего наименьшего и наибольшего значений функции, непрерывной на отрезке.
Если функция 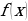 непрерывна на отрезке
непрерывна на отрезке 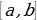 ,то она достигает на этом отрезке своего наибольшего и наименьшего значений.
,то она достигает на этом отрезке своего наибольшего и наименьшего значений.
Контрольные вопросы:
Что называется пределом функции в точке?
В чем геометрический смысл предела функции?
Какая функция называется бесконечно большой? Бесконечно малой?
Какие замечательные пределы вы знаете?
Какая функция называется непрерывной в точке? Непрерывной справа? Непрерывной слева? Непрерывной на интервале? Непрерывной на отрезке?
Какая точка называется точкой разрыва?
Какая точка называется точкой разрыва 1-го рода? 2-го рода?







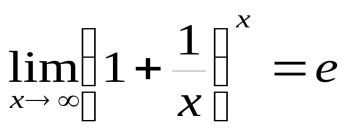 .
.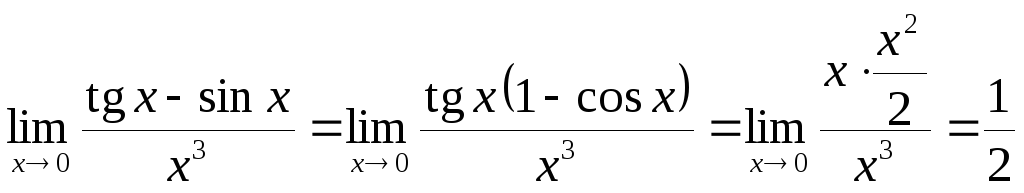
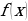 , определенная в некоторой окрестности точки
, определенная в некоторой окрестности точки 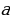 , называется непрерывной в точке
, называется непрерывной в точке 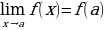 .
.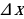 соответствует бесконечно малое приращение функции
соответствует бесконечно малое приращение функции 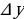 , то есть
, то есть 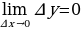 .
. и
и 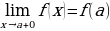 , т.е.
, т.е. 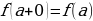 , то эта функция называется непрерывной справа в точке
, то эта функция называется непрерывной справа в точке 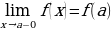 , т.е.
, т.е. 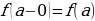 , то эта функция называется непрерывной слева в точке
, то эта функция называется непрерывной слева в точке 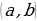 , то она называется непрерывной на этом интервале.
, то она называется непрерывной на этом интервале.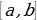 , если она непрерывна на интервале
, если она непрерывна на интервале 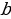 .
.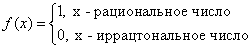
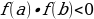 , то на интервале
, то на интервале 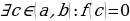 .
.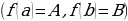 , то для любого числа C, лежащего между A и B, на интервале
, то для любого числа C, лежащего между A и B, на интервале 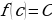 .
.









