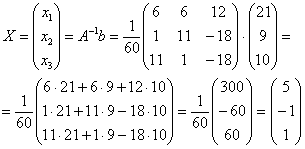Системы линейных уравнений
Основные понятия. Решение систем линейных уравнений
В курсе высшей математики системы линейных уравнений требуется решать как в виде отдельных заданий, так и в ходе решения остальных задач. С системами линейных уравнений приходится иметь дело практически во всех разделах высшей математики.
Что в данном случае обозначает математическое слово «линейных»? Это значит, что в уравнения системы все переменные входят в первой степени: 
Решить систему уравнений – это значит найти множество её решений или доказать, что их нет
1. Решение системы линейных уравнений способом подстановки
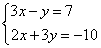
Рассмотрим пример
1) Выразить в одном из уравнений переменную. Например, выразим y в первом уравнении, получим систему:
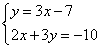
2) Подставляем во второе уравнение системы вместо y выражение 3х-7:
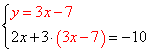
3) Решаем полученное второе уравнение:

4) Полученное решение подставляем в первое уравнение системы:
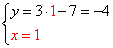
Система уравнений имеет единственное решение: пару чисел x = 1, y = - 4. Ответ: (1; -4), записывается в скобках, на первой позиции значение x, на второй - y.
2. Решение системы линейных уравнений способом сложения
Решим систему уравнений из предыдущего примера методом сложения.
1) Преобразовать систему таким образом, чтобы коэффициенты при одной из переменных стали противоположными. Умножим первое уравнение системы на "3".

2) Складываем почленно уравнения системы. Второе уравнение системы (любое) переписываем без изменений.

3) Полученное решение подставляем в первое уравнение системы:
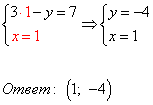
3. Решение системы линейных уравнений графическим способом
Графическое решение системы уравнений с двумя переменными сводится к отыскиванию координат общих точек графиков уравнений.
Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может: а) иметь единственное решение; б) не иметь решений; в) иметь бесконечное множество решений.
2 ) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.
) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.
Графическое решение системы
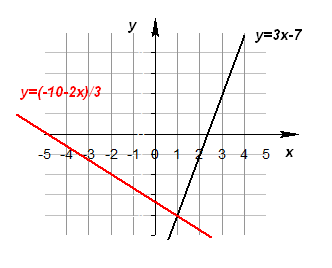
Ответ: (1; -4).
4.Решение системы по формулам Крамера
Рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. 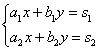
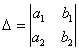
На первом шаге вычислим определитель , его называют главным определителем системы.
Если  , то система имеет бесконечно много решений или несовместна (не имеет решений).
, то система имеет бесконечно много решений или несовместна (не имеет решений).
Если 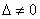 , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
, то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
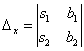 и
и 
Корни уравнения находим по формулам:
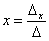 ,
, 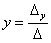
Пример. Решить систему линейных уравнений

Решение:
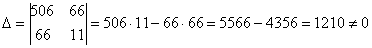 , значит, система имеет единственное решение.
, значит, система имеет единственное решение.
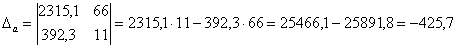 ;
;
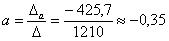
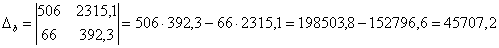 ;
;

Ответ: 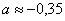 ,
, 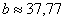
Пример. Решить систему по формулам Крамера. Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Пример. Решить систему по формулам Крамера.
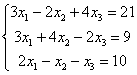
Ответ:  .
.
5. Метод Гаусса (последовательного исключения неизвестных).
 решим ее методом Гаусса.
решим ее методом Гаусса.
На первом этапе нужно записать расширенную матрицу системы:
 .
.
Матрица системы – это матрица, составленная только из коэффициентов при неизвестных, в данном примере матрица системы: 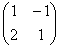 . Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае:
. Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае:  . Любую из матриц можно для краткости называть просто матрицей.
. Любую из матриц можно для краткости называть просто матрицей.
После того, как расширенная матрица системы записана, с ней необходимо выполнить некоторые действия, которые также называются элементарными преобразованиями.
Существуют следующие элементарные преобразования:
1) Строки матрицы можно переставлять местами. Например, в рассматриваемой матрице можно безболезненно переставить первую и вторую строки: 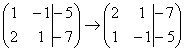
2) Если в матрице есть (или появились) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной.
3) Если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить.
4) Строку матрицы можно умножить (разделить) на любое число, отличное от нуля.
5) К строке матрицы можно прибавить другую строку, умноженную на число, отличное от нуля.
Элементарные преобразования не меняют решение системы уравнений
Цель элементарных преобразований – привести матрицу к ступенчатому виду: 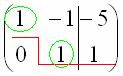 . треугольный вид.
. треугольный вид.
Ответ: 
Пример 1
Решить методом Гаусса систему уравнений:
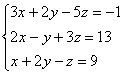
Ответ: 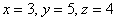
6. Решение системы с помощью обратной матрицы
Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.
Пример 11
Решить систему с матричным методом
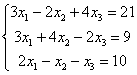
Решение: Запишем систему в матричной форме:
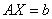 , где
, где 
если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице  нужно было бы поставить нули.
нужно было бы поставить нули.
Согласно формуле нам нужно найти обратную матрицу  и выполнить матричное умножение
и выполнить матричное умножение 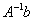 .
.
Обратную матрицу найдем по формуле:
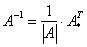 , где
, где 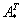 – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы  .
.
Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.
Внимание! Если  , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса).
, то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса).
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров 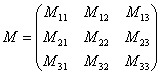
Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:
 То есть, двойной подстрочный индекс указывает, что элемент
То есть, двойной подстрочный индекс указывает, что элемент 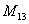 находится в первой строке, третьем столбце, а, например, элемент
находится в первой строке, третьем столбце, а, например, элемент  находится в 3 строке, 2 столбце
находится в 3 строке, 2 столбце
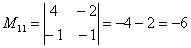
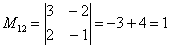
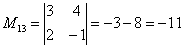

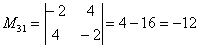
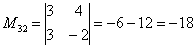
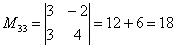
Таким образом:
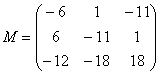 – матрица миноров соответствующих элементов матрицы
– матрица миноров соответствующих элементов матрицы  .
.
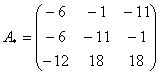 – матрица алгебраических дополнений.
– матрица алгебраических дополнений.
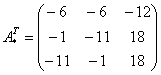 – транспонированная матрица алгебраических дополнений.
– транспонированная матрица алгебраических дополнений.

Ни в коем случае не вносим 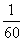 в матрицу, это серьезно затруднит дальнейшие вычисления. Деление нужно было бы выполнить, если бы все числа матрицы делились на 60 без остатка. А вот внести минус в матрицу в данном случае очень даже нужно, это, наоборот – упростит дальнейшие вычисления.
в матрицу, это серьезно затруднит дальнейшие вычисления. Деление нужно было бы выполнить, если бы все числа матрицы делились на 60 без остатка. А вот внести минус в матрицу в данном случае очень даже нужно, это, наоборот – упростит дальнейшие вычисления.
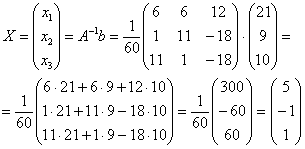
Ответ: 
Контрольные вопросы:
Какие уравнения называются линейными?
Что значит решить систему линейных уравнений?
Как решить систему линейных уравнений способом подстановки?
Как решить систему линейных уравнений способом сложения?
Как решить систему линейных уравнений графическим способом?
Как решить систему линейных уравнений по формулам Крамера?
Как решить систему линейных уравнений методом Гаусса (последовательного исключения неизвестных)?
Как решить систему линейных уравнений с помощью обратной матрицы?






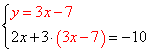


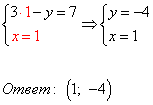

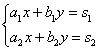
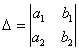
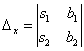 и
и 
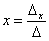 ,
, 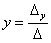

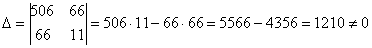 , значит, система имеет единственное решение.
, значит, система имеет единственное решение.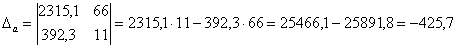 ;
;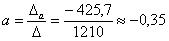
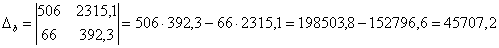 ;
;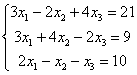
 .
. 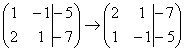
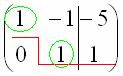 . треугольный вид.
. треугольный вид. 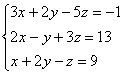


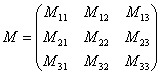
 То есть, двойной подстрочный индекс указывает, что элемент
То есть, двойной подстрочный индекс указывает, что элемент 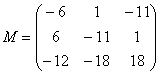 – матрица миноров соответствующих элементов матрицы
– матрица миноров соответствующих элементов матрицы 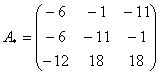 – матрица алгебраических дополнений.
– матрица алгебраических дополнений.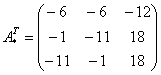 – транспонированная матрица алгебраических дополнений.
– транспонированная матрица алгебраических дополнений.