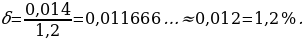ТО 107 законспектировать лекцию. Прислать на почту nata.vodiahina2014@yandex.ru
Тема урока: Целые и рациональные числа. Действительные числа. Приближенные вычисления. Погрешности приближений.
Цели:
Образовательные:
- рассмотреть множество натуральных, целых, рациональных чисел;
- ввести понятие конечной и бесконечной десятичной дроби;
- дать определение бесконечной периодической десятичной дроби.
- сформировать умение переводить обыкновенную дробь в десятичную;
- сформировать умение переводить бесконечную периодическую дробь в обыкновенную;
-рассмотреть множество иррациональных чисел;
- рассмотреть множество действительных чисел;
- рассмотреть правила выполнения действий с бесконечными десятичными дробями;
- ввести понятие модуля действительного числа.
Воспитательные:
- воспитывать положительное отношение к приобретению новых знаний;
- воспитывать ответственность за свои действия и поступки;
- вызвать заинтересованность новым для студентов подходом изучения математики.
Развивающие:
- формировать навыки познавательного мышления;
- формировать умения и навыки учебного труда.
Ход урока
1. Изучение нового материала
Первое множество, которое вы изучили в математике это множество натуральных чисел, т. е. числа которые мы используем в счете N= 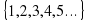 . Если мы сложим и умножим натуральные числа, то всегда получим натуральное число. Однако при нахождении разности и частного не всегда получается натуральное число.
. Если мы сложим и умножим натуральные числа, то всегда получим натуральное число. Однако при нахождении разности и частного не всегда получается натуральное число.
А если к множеству натуральных чисел добавим числа противоположные натуральным и 0, то получим множество целых чисел Z=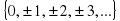 . При сложении, вычитании и умножении целых чисел всегда получаются целые числа. Однако частное двух целых чисел может не быть целым числом.
. При сложении, вычитании и умножении целых чисел всегда получаются целые числа. Однако частное двух целых чисел может не быть целым числом.
Введение множества рациональных чисел Q, т. е. чисел вида 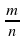 ,
,
где т — целое число, n — натуральное число. Любое целое число можно представить в виде рационального числа, как например число m можно представить в виде 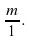
Мы всегда получим рациональное числа при выполнении четырех арифметических действий (кроме деления на нуль) над рациональными числами всегда.
Так же рациональное число можно представить в виде дроби 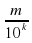 ,
,
где т — целое число, k — натуральное число, а так же его можно записать в виде конечной десятичной дроби.
Например: 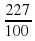 можно записать, как 2,27; -
можно записать, как 2,27; - 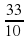 можно записать, как - 3,3.
можно записать, как - 3,3.
Но рациональные числа, например, такие как 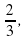 -
-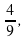
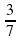 нельзя записать в виде конечной десятичной дроби. Если
нельзя записать в виде конечной десятичной дроби. Если 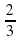 попытаться записать — в виде десятичной дроби, то получится бесконечная десятичная дробь 0,666... . Бесконечную десятичную дробь 0,666... называют периодической, повторяющуюся цифру 6 — ее периодом. Периодическую дробь 0,666... коротко записывают так: 0,(6); читается: «Ноль целых и шесть в периоде».
попытаться записать — в виде десятичной дроби, то получится бесконечная десятичная дробь 0,666... . Бесконечную десятичную дробь 0,666... называют периодической, повторяющуюся цифру 6 — ее периодом. Периодическую дробь 0,666... коротко записывают так: 0,(6); читается: «Ноль целых и шесть в периоде».
Любая периодическая дробь — это бесконечная десятичная дробь, у которой, начиная с некоторого десятичного знака, повторяется одна и та же цифра или несколько цифр — период дроби.
Например, десятичная дробь 23,14565656... = 23,14(56) периодическая с периодом 56; читается «23 целых, 14 сотых и 56 в периоде».
Заметим, что каждое целое число или конечную десятичную дробь можно считать и бесконечной десятичной периодической дробью с периодом, равным нулю.
Например: 41 = 41,000... = 41,(0); 4,53 = 4,53000... = 4,53(0).
Итак, каждое рациональное число можно представить в виде бесконечной периодической десятичной дроби.
Справедливо и обратное утверждение: каждая бесконечная периодическая десятичная дробь является рациональным числом, так как может быть представлена в виде дроби 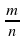 , где т — целое число, n — натуральное число.
, где т — целое число, n — натуральное число.
Периодические дроби бывают чистыми и смешанными.
Чистой п.д. называется дробь, у которой период начинается сразу же после запятой, например, 3,171717…Смешанной п.д. называется дробь, у которой между запятой и первым периодом есть одна или несколько неповторяющихся цифр, например, 0,23191919…
Правило 1. Чтобы обратить чистую п.д.д. в обыкновенную, нужно её период сделать числителем, а в знаменатель записать цифру 9 столько раз, сколько цифр в периоде.
Например: 0,(6)=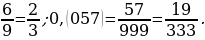
Правило 2. Чтобы обратить смешанную п.д.д. в обыкновенную, достаточно из числа, стоящего до второго периода, вычесть число, стоящее до первого периода, и полученную разность взять числителем, а знаменателем написать цифру 9 столько раз, сколько цифр в периоде, со столькими нулями, сколько цифр между запятой и периодом.
Например: 0,5(3)=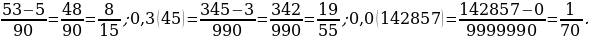
Исключение: б.п.д.д. с периодом 9. Например: 0,6(9)=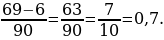
Иррациональным числом (I) называется бесконечная десятичная непериодическая дробь. Например, число 0,123456…., в котором после запятой записаны подряд все натуральные числа, является положительным иррациональным числом. Число -5, 246810…., в котором после запятой записаны подряд все четные числа, является отрицательным иррациональным числом.
Числа 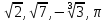 также являются иррациональными, так как можно доказать, что они могут быть представлены в виде бесконечных десятичных непериодических дробей.
также являются иррациональными, так как можно доказать, что они могут быть представлены в виде бесконечных десятичных непериодических дробей.
Рациональные и иррациональные числа образуют множество действительных чисел (R).
Известно как выполняются действия над конечными десятичными дробями. Арифметические операции над действительными числами, т.е. бесконечными десятичными дробями, заменяются операциями над их приближениями.
Например, вычислим приближенные значения 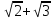
Решение:
-
Воспользуемся калькулятором и найдем значения 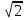 и
и 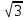
Имеем 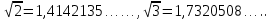
-
Найдем 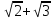 с точностью до единицы
с точностью до единицы
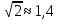 и
и 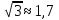 , тогда
, тогда 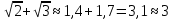
-
Найдем 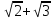 с точностью до одной десятой
с точностью до одной десятой
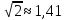 и
и 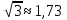 , тогда
, тогда 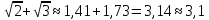
-
Найдем 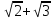 с точностью до одной сотой
с точностью до одной сотой
 и
и 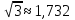 , тогда
, тогда 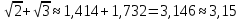
Аналогично, вычисляя произведение 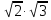 с точностью до 0,1, получаем
с точностью до 0,1, получаем
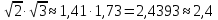
Результат действий с приближенными числами есть тоже приближенное число. Выполняя некоторые действия над точными числами (деление, извлечение корня), можно также получить приближенные числа.
Абсолютная и относительная погрешности приближённых значений чисел
Разность между точным числом х и его приближенным значением а называется абсолютной погрешностью приближенного числа и обозначается через 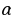 , т.е.
, т.е. 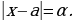
Например, если точное число 1,214 округлить до десятых, получим приближенное число 1,2. В данном случае абсолютная погрешность приближенного числа 1,2 равна 1,214 - 1,2, т.е. 0,014.
Относительной погрешностью 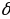 называется отношение абсолютной погрешности
называется отношение абсолютной погрешности 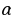 к величине приближенного числа a.:
к величине приближенного числа a.: 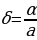 . Относительную погрешность принято выражать в процентах.
. Относительную погрешность принято выражать в процентах.
Например, 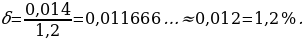
2. Закрепление изученного.
Учебник: Алгебра и начала математического анализа,10-11. Ш. А. Алимов, Ю. М. Колягин и др. Код доступа: https://yadi.sk/i/9LtBXH5sIo2s-A
№ 1 (1,3,5), 2(1,3,5), 3(1,3,5) – стр. 6, № 9 – стр.10, Ш. А. Алимов
3. Итоги урока.
4. Домашняя самостоятельная работа: № 1, 2, 3, 6 – чётные номера






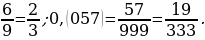
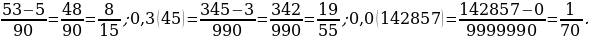
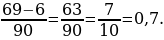
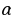 , т.е.
, т.е. 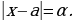
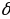 называется отношение абсолютной погрешности
называется отношение абсолютной погрешности 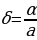 . Относительную погрешность принято выражать в процентах.
. Относительную погрешность принято выражать в процентах.