Возрастание и убывание функции. Точки экстремума. Исследование функции на экстремум с помощью производных высших порядков. Выпуклость и вогнутость кривой. Точки перегиба. Асимптоты. Общая схема исследования функций
Теорема 1. (Достаточное условие возрастания функции)
Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на интервале (a, b), причем  (x) 0 для любого x(a, b), то эта функция возрастает на отрезке [a, b].
(x) 0 для любого x(a, b), то эта функция возрастает на отрезке [a, b].
Теорема 2. (Необходимое условие возрастания функции)
Если функция f(x) непрерывна и возрастает на отрезке [a, b], дифференцируема на интервале (a, b), то  (x 0 для) любого x из интервала (a, b).
(x 0 для) любого x из интервала (a, b).
Сформулируйте и докажите достаточное условие и необходимое условие для убывания функции.
П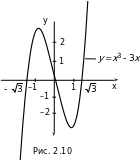
ример. Исследовать на монотонность (т.е. возрастание и убывание) функцию:
f (x) = x3 – 3x.
Решение.  (x) = 3x2 – 3 = 3(x2 – 1).
(x) = 3x2 – 3 = 3(x2 – 1).
Неравенство  (x) 0, т.е. 3(x2 – 1) 0, справедливо для x x 1. Следовательно, функция f(x, –1)) возрастает на интервалах (– и ). Поскольку неравенство(1, +
(x) 0, т.е. 3(x2 – 1) 0, справедливо для x x 1. Следовательно, функция f(x, –1)) возрастает на интервалах (– и ). Поскольку неравенство(1, +  (x) x2 – 1) x(–1, 1), то на интервале (–1, 1) функция f(x) убывает.
(x) x2 – 1) x(–1, 1), то на интервале (–1, 1) функция f(x) убывает.
Построим график функции y = x3 – 3x (рис. 2.10), используя ее значения в точках:
x1 = –1, x2 = 1, x3 = 0, x4 = –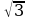 , x5 =
, x5 =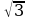 :
:
f(–1) = 2, f(1) = –2, f(0) = 0, f(–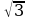 ) = 0, f(
) = 0, f(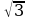 ) = 0.
) = 0.
Заметим, что в точке x1 = –1 значение f(–1) больше, чем значение f(x) в соседних с x1 точках. Говорят, что в точке x1 функция имеет максимум (локальный максимум). Аналогично, f(x2) f(x) для x, близких к x2. В этом случае говорят, что в точках x2 функция имеет минимум (локальный минимум).
Экстремумы функции
Говорят, что в точке x0 функция f(x) имеет максимум, если существует такая окрестность точки x0, что для любого x из этой окрестности f(x) f(x0).
Точка x0 называется точкой минимума, если существует такая окрестность точки x0, что для любого x из этой окрестности f(x) f(x0).
Точки максимума и минимума называются точками экстремума.
Замечание. Точки экстремума всегда являются внутренними точками промежутка, т.е. не могут быть его концом.
Теорема 1. (Необходимое условие экстремума)
Если функция f(x) дифференцируема в точке x0 и некоторой ее окрестности и x0 – точка экстремума, то  (x0) = 0.
(x0) = 0.
Следствие. Если x0 – точка экстремума, то  (x0) = 0 или
(x0) = 0 или  (x0) не существует.
(x0) не существует.
Если f'(x0) = 0 или f'(x0) не существует, то точку x0 будем называть критической (или подозрительной на экстремум). Критическая точка может и не быть точкой экстремума.
Теорема 2. (Первое достаточное условие экстремума)
Пусть функция f (x) определена и непрерывна в точке x0 и некоторой ее окрестности, дифференцируема в этой окрестности, за исключением, может быть, точки x0, и x0 – критическая точка для функции f (x) (т.е.  (x0) = 0 или
(x0) = 0 или  (x0) не существует). Тогда: 1) если при x x0 производная
(x0) не существует). Тогда: 1) если при x x0 производная  (x) 0, а для x x0:
(x) 0, а для x x0:  (x) x0 – точка максимума; 2) если при x x0:
(x) x0 – точка максимума; 2) если при x x0:  (x) x x0:
(x) x x0:  (x) 0, то x0 – точка минимума.
(x) 0, то x0 – точка минимума.
Теорема 3. (Второе достаточное условие экстремума).
Пусть функция f (x) дважды дифференцируема в точке x0 и некоторой ее окрестности и пусть  (x0) = 0. Если
(x0) = 0. Если 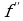 (x0) 0, то x0 – точка минимума. Если
(x0) 0, то x0 – точка минимума. Если 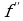 (x0) x0 – точка максимума.
(x0) x0 – точка максимума.
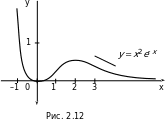
Пример 1. Исследовать на монотонность и экстремумы функцию
f(x) = x2e–x. Построить ее график.
Решение. Эта функция определена и непрерывна на всей ). Найдем производную:, числовой оси (–  (x) = 2xe–x – x2e–x = xe–x(2 – x). Тогда
(x) = 2xe–x – x2e–x = xe–x(2 – x). Тогда  (x) = 0 при x1 = 0 и x2 = 2, где x1, x2 – критические точки. ; 0), (0; 2), (2;Эти точки разбивают всю числовую ось на три интервала: (– ). Составим таблицу, в первой строке которой поместим указанные точки и+ интервалы, во второй строчке – сведения о производной
(x) = 0 при x1 = 0 и x2 = 2, где x1, x2 – критические точки. ; 0), (0; 2), (2;Эти точки разбивают всю числовую ось на три интервала: (– ). Составим таблицу, в первой строке которой поместим указанные точки и+ интервалы, во второй строчке – сведения о производной  (x) в точках и на интервалах, а в третьей – поведение данной функции f(x):
(x) в точках и на интервалах, а в третьей – поведение данной функции f(x):
| x | 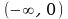
| x1 = 0 | (0, 2) | x2 = 0 | 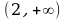
|
|  (x) (x)
|  (x) (x)
| 0 |  (x) 0 (x) 0
| 0 |  (x) (x)
|
| f(x) | убывает | 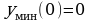
| возрастает | 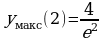
| убывает |
Определим знак  (x) на каждом из интервалов: если x, 0),(– то
(x) на каждом из интервалов: если x, 0),(– то  (x) x(0, 2), то
(x) x(0, 2), то  (x)0; если x), то(2, +
(x)0; если x), то(2, +  (x) f(x): на первом и последнем интервалах f(x) убывает, а на втором – возрастает. Отсюда следует, что x1 = 0 является точкой минимума, yмин(0) = 0, а x2 = 2 – точка максимума, yмакс(2) =
(x) f(x): на первом и последнем интервалах f(x) убывает, а на втором – возрастает. Отсюда следует, что x1 = 0 является точкой минимума, yмин(0) = 0, а x2 = 2 – точка максимума, yмакс(2) =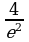 0,54. Для построения графика заметим, что f (x) 0 для всех x, отличных от нуля, и
0,54. Для построения графика заметим, что f (x) 0 для всех x, отличных от нуля, и
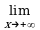
x2e–x = 0,
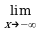 x2e–x ,= f(–1) = e 2,7.
x2e–x ,= f(–1) = e 2,7.
График этой функции изображен на рис. 2.12.
Отметим, что дальнейшее исследование этой функции (см. следующий раздел) позволит уточнить ее график.
Пример 2. Исследовать на экстремум функцию f (x) = x + 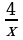 .
.
Решение(0,, 0). Область определения функции (- ), в каждом из этих интервалов функция непрерывна. Найдем+ f'(x) и f''`(x): f `(x) = 1 – 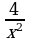 , f''(x) =
, f''(x) = 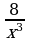 . Теперь найдем критические точки функции, для этого решим уравнение f'(x) = 0:
. Теперь найдем критические точки функции, для этого решим уравнение f'(x) = 0:
1 – 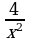 = 0, отсюда x1 = –2, x2 = +2 – критические точки. Используем теорему 3 для исследования критических точек, для этого вычислим f''(x) в точках x1 и x2. Так как
= 0, отсюда x1 = –2, x2 = +2 – критические точки. Используем теорему 3 для исследования критических точек, для этого вычислим f''(x) в точках x1 и x2. Так как
f''(–2) = 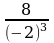 = –1x1 = –2 является точкой максимума fмакс(–2) = –2 –
= –1x1 = –2 является точкой максимума fмакс(–2) = –2 – 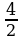 = –4. Для x2: f''(2) =
= –4. Для x2: f''(2) = 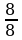 = 1 0, поэтому x2 = 2 – точка минимума, fмин(2) = 2 +
= 1 0, поэтому x2 = 2 – точка минимума, fмин(2) = 2 + 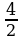 = 4.
= 4.
Т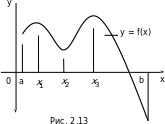
аким образом, функция f(x) = x + 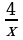 имеет максимум при x1 = –2, f(–2) = –4 и имеет минимум при x2 = 2, f(2) = 4.
имеет максимум при x1 = –2, f(–2) = –4 и имеет минимум при x2 = 2, f(2) = 4.
Известно, что если функция непрерывна на отрезке, то она достигает на этом отрезке своего наименьшего значения и своего наибольшего значения (см. гл. 1). Иногда требуется найти наименьшее или наибольшее значение такой функции.
Если на отрезке [a, b] есть точки минимума и максимума функции f(x) (рис. 2.13), то наименьшее значение функция будет принимать либо в одной из точек минимума, либо на конце отрезка [a, b]. Аналогично для наибольшего значения.
Алгоритм нахождения наибольшего и наименьшего значений функции f(x), непрерывной на отрезке:
найти критические точки x1, x2, ..., xn функции f(x), принадлежащие отрезку 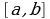 ;
;
вычислить значения функции f (x) в критических точках и на концах отрезка;
из этих значений выбрать самое большое и самое малое, эти числа и будут наибольшим и наименьшим значениями f(x) на отрезке [a, b].
Пример 3. Найти наименьшее и наибольшее значения функции:
f(x) = x4 – 2x2 + 5 на отрезке [–2, 2].
Решение. Найдем критические точки для данной функции:
 (x) = 4x3 – 4x = 4x(x2 – 1);
(x) = 4x3 – 4x = 4x(x2 – 1);
 (x) = 0 при x1 = 0, x2 = –1, x3 = +1, все три критические точки принадлежат данному отрезку. Вычислим значения функции в точках –2, –1, 0, 1, 2:
(x) = 0 при x1 = 0, x2 = –1, x3 = +1, все три критические точки принадлежат данному отрезку. Вычислим значения функции в точках –2, –1, 0, 1, 2:
f(–2) = (–2)4 (–2)– 22 + 5 = 16 – 8 + 5 = 13, f(–1) = 1 – 2 + 5 = 4,
f(0) = 5, f(1) = 4, f(2) =13.
Из найденных значений самое малое число 4, а самое большое число 13.
Итак, наименьшее значение функции равно 4, наибольшее значение равно 13.
Выпуклость, вогнутость графика функции,
точки перегиба
Пусть f(x) – функция, дифференцируемая на интервале (a, b). Рассмотрим кривую, являющуюся графиком функции y = f(x).
Кривая, заданная функцией y = f(x), называется выпуклой на интервале (a, b), если все точки кривой лежат ниже любой ее касательной на этом интервале.
Кривая называется вогнутой на интервале (a, b), если все точки кривой лежат выше любой ее касательной на этом интервале.
Точка кривой M0(x0, f(x0)), отделяющая выпуклую ее часть от вогнутой, называется точкой перегиба.
Теорема 1. (Достаточные условия выпуклости и вогнутости графика функции).
Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна, т.е. f''(x) y = f(x) на этом интервале выпукла.
Если во всех точках интервала (a, b): 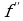 (x) 0, то кривая y = f(x) на этом интервале вогнута. (правило дождя)
(x) 0, то кривая y = f(x) на этом интервале вогнута. (правило дождя)
Теорема 2 (достаточное условие точки перегиба)
Пусть кривая является графиком функции y = f(x). Если 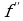 (x0) = 0 или
(x0) = 0 или 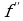 (x0) не существует и при переходе через x0 вторая производная
(x0) не существует и при переходе через x0 вторая производная 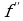 (x) меняет свой знак, то точка M0(x0, f(x0)) этой кривой является точкой перегиба.
(x) меняет свой знак, то точка M0(x0, f(x0)) этой кривой является точкой перегиба.
Асимптоты
При исследовании функции часто приходится устанавливать вид ее графика (а, значит, и характер функции) при неограниченном удалении точки графика от начала координат (при стремлении переменной точки в бесконечность). При этом важным случаем является тот, когда график функции при удалении его переменной точки в бесконечность неограниченно приближается к некоторой прямой.
Асимптотой графика функции y = f(x) называется такая прямая, что расстояние от переменной точки M на графике до этой прямой стремится к нулю при удалении точки M в бесконечность (рис. 2.17, 2.18).
С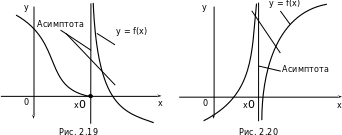
примерами асимптот мы встречались при изучении пределов функции (глава 1). Напомним, что если 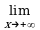 f (x) = b, то прямая y = b является асимптотой графика
f (x) = b, то прямая y = b является асимптотой графика
y = f(x) (при x ), эта асимптота параллельна оси Ox и называется горизонтальной асимптотой (см. рис. 2.18). Аналогично, прямая y = b является асимптотой графика
y = f(x) при x , если 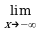 f (x) = b (рис. 2.17).Рассмотрим асимптоты, параллельные оси Oy. Они называются вертикальными асимптотами.
f (x) = b (рис. 2.17).Рассмотрим асимптоты, параллельные оси Oy. Они называются вертикальными асимптотами.
П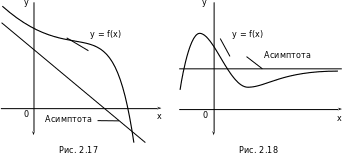
усть для функции f (x): 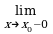 f(x или) =
f(x или) = 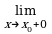 f(x, тогда из определения асимптоты) = следует, что прямая x = x0 асимптота. Очевидно и обратное, если прямая
f(x, тогда из определения асимптоты) = следует, что прямая x = x0 асимптота. Очевидно и обратное, если прямая
x = x0 является асимптотой, то хотя бы один из пределов, 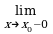 f(x),
f(x), 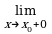 f(x), является бесконечным (см. рис. 2.19, 2.20).
f(x), является бесконечным (см. рис. 2.19, 2.20).
Следовательно, для отыскания вертикальных асимптот нужно найти такие значения x0, односторонние пределы в которых равны бесконечности.
Пример 1. Найти вертикальные асимптоты для графика функции y =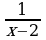 .
.
Решение. Функция f(x) = 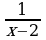 определена и непрерывна во всех точках числовой оси, за исключением точки x0 = 2, в которой функция терпит разрыв,
определена и непрерывна во всех точках числовой оси, за исключением точки x0 = 2, в которой функция терпит разрыв,
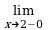
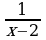 ,= –
,= – 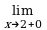
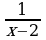 . Следовательно, прямая= + x = 2 является вертикальной асимптотой для графика y =
. Следовательно, прямая= + x = 2 является вертикальной асимптотой для графика y =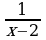 . Кроме того,
. Кроме того, 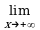
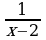 = 0 и
= 0 и 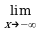
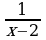 = 0, следовательно, прямая y = 0 является горизонтальной асимптотой при x и при x (см. рис. 2.21).
= 0, следовательно, прямая y = 0 является горизонтальной асимптотой при x и при x (см. рис. 2.21).
Рассмотрим асимптоты, которые не параллельны оси Oy, будем называть их наклонными асимптотами. Пусть график функции y = f(x) имеет наклонную асимптоту при x , тогда ее уравнение имеет вид y = kx + b. Определим числа k и b.
Опустим из точки M(x, f(x)) графика функции перпендикуляр MN на асимптоту (см. рис. 2.22). Из определения асимптоты следует, что при x длина MN 0 (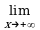 MN = 0). Из MNK имеем MK =
MN = 0). Из MNK имеем MK =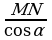 , где – угол наклона асимптоты к оси Ox, поэтому cos –постоянная величина. Значит,
, где – угол наклона асимптоты к оси Ox, поэтому cos –постоянная величина. Значит, 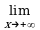 MK = 0. Так как MK = |AK – AM|,
MK = 0. Так как MK = |AK – AM|,
AK = kx + b, то MK = |kx + b – f(x)|, следовательно,
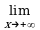 (f(x) – kx – b) = 0. (2.31)
(f(x) – kx – b) = 0. (2.31)
Итак, если прямая y = kx + b является асимптотой графика функции y = f (x), то выполняется равенство (2.31) и наоборот, если при постоянных числах k, b выполняется равенство (2.31), то прямая y = kx + b является асимптотой. Из равенства (2.31), разделив бесконечно малую функцию (f(x) – kx – b) на x (а x ), получим:
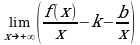 = 0, (2.32)
= 0, (2.32)
о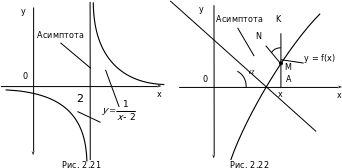
тсюда угловой коэффициент асимптоты:
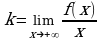 . (2.33)
. (2.33)
Определим коэффициент b из равенства (2.31), подставив в это равенство значение k:
b = 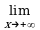 (f(x) – kx). (2.34)
(f(x) – kx). (2.34)
Итак, если прямая y = kx + b является асимптотой графика y = f(x), то k, b находятся по формулам (2.33), (2.34). Обратно, если существуют пределы (2.33), (2.34), то прямая y = kx + b есть асимптота. Если хотя бы один из пределов (2.33), (2.34) не существует, то при x кривая не имеет асимптоты.
Аналогично решается вопрос об асимптотах при x . Заметим, что отдельно находить горизонтальные асимптоты нет надобности, они будут найдены при нахождении наклонных асимптот (при k = 0).
Пример 2. Найти асимптоты линии y = ex – x.
Решение. Функция f (x) = ex – x определена, непрерывна на бесконечном интервале ), поэтому вертикальных асимптот нет., +(–
Найдем наклонные асимптоты, для этого вычислим пределы (2.33), (2.34) при
x , x :
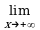
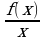 =
= 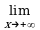 (
(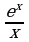 ,– 1) =
,– 1) =
так как 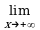
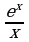 (проверьте= это по правилу Лопиталя). Отсюда следует, что при
(проверьте= это по правилу Лопиталя). Отсюда следует, что при
x наклонных асимптот нет:
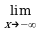
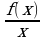 =
= 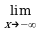 (
(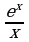 – 1) = –1, так как
– 1) = –1, так как 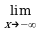
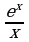 = 0,
= 0,
отсюда k = –1. Далее, 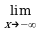 (f(x) – kx) =
(f(x) – kx) = 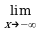 (ex – x + x) =
(ex – x + x) = 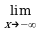 ex = 0, значит, b = 0.
ex = 0, значит, b = 0.
Итак, прямая y = –x есть наклонная асимптота при x для графика функции y = ex – x.
Контрольные вопросы:
Каково достаточное условие возрастания / убывания функции?
Каково необходимое условие возрастания / убывания функции?
Какие точки называются точками экстремума?
Как найти наибольшее и наименьшее значения функции на отрезке?
Когда кривая называется выпуклой / вогнутой на отрезке?
Какая точка называется точкой перегиба?
Что называется асимптотой графика? Какие бывают асимптоты?






 (x) 0 для любого x(a, b), то эта функция возрастает на отрезке [a, b].
(x) 0 для любого x(a, b), то эта функция возрастает на отрезке [a, b].
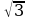 , x5 =
, x5 =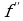 (x0) 0, то x0 – точка минимума. Если
(x0) 0, то x0 – точка минимума. Если 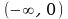
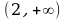
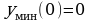
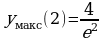
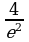 0,54. Для построения графика заметим, что f (x) 0 для всех x, отличных от нуля, и
0,54. Для построения графика заметим, что f (x) 0 для всех x, отличных от нуля, и 

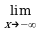 x2e–x ,= f(–1) = e 2,7.
x2e–x ,= f(–1) = e 2,7.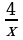 .
.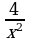 , f''(x) =
, f''(x) = 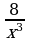 . Теперь найдем критические точки функции, для этого решим уравнение f'(x) = 0:
. Теперь найдем критические точки функции, для этого решим уравнение f'(x) = 0: 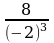 = –1x1 = –2 является точкой максимума fмакс(–2) = –2 –
= –1x1 = –2 является точкой максимума fмакс(–2) = –2 – 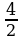 = –4. Для x2: f''(2) =
= –4. Для x2: f''(2) = 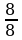 = 1 0, поэтому x2 = 2 – точка минимума, fмин(2) = 2 +
= 1 0, поэтому x2 = 2 – точка минимума, fмин(2) = 2 + 
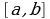 ;
;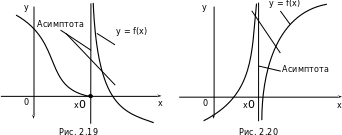
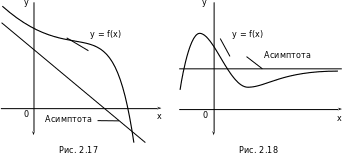
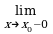 f(x или) =
f(x или) = 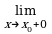 f(x, тогда из определения асимптоты) = следует, что прямая x = x0 асимптота. Очевидно и обратное, если прямая
f(x, тогда из определения асимптоты) = следует, что прямая x = x0 асимптота. Очевидно и обратное, если прямая 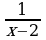 .
.
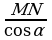 , где – угол наклона асимптоты к оси Ox, поэтому cos –постоянная величина. Значит,
, где – угол наклона асимптоты к оси Ox, поэтому cos –постоянная величина. Значит, 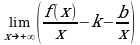 = 0, (2.32)
= 0, (2.32)
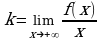 . (2.33)
. (2.33)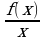 =
= 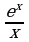 ,– 1) =
,– 1) = 
















