Реферат на тему «Арифметическая и геометрическая прогрессии в окружающей нас жизни»

Муниципальное общеобразовательное учреждение «Аладьинская школа»

Тема работы: «Арифметическая и геометрическая прогрессии в окружающей нас жизни»

Выполнила: Гусейнова Милена Ильгаровна, ученица 9 класса.

Руководитель:Бортникова Татьяна Александровна, учитель физики и математики I категории

С. Аладьино

2019

«Арифметические и геометрические прогрессии в задачах практического содержания»

Введение

Девизом одного из наших уроков, когда мы решали задачи на арифметическую и геометрическую прогрессии, стали слова Иоганна Гете «Недостаточно только получить знание, надо найти ему приложение». Они запали мне в душу.

Актуальность: Наша жизнь полна различных вычислений. Математические знания помогают в практической деятельности, формирует представление о математике как о части человеческой культуры. Всё, что не применяется, очень быстро забывается, так как становится ненужным. В 9 классе мы изучали арифметическую и геометрическую прогрессии. Присмотревшись внимательнее, я заметила, что они имеют определенное практическое значение. Передо мной стал вопрос: в каких жизненных ситуациях можно применить знания о прогрессиях? Можно ли увидеть прогрессию в природе, экономике других областях человеческой жизни.Впереди меня ждут экзамены, и я решила подготовиться, решая задачи на прогрессии с прикладным содержанием.

Я стала обращать внимание, что в средствах массовой информации часто звучат выражения «…увеличивается с геометрической прогрессией…», «…уменьшается по закону арифметической прогрессии…» и др.

Таким образом, объектом моего исследования являются арифметическая и геометрическая прогрессия.

Цель моего исследования: практико-ориентированные задачи на арифметическую и геометрическую прогрессий.

Для этого я поставила перед собой следующие задачи.

1. Изучить наличие задач на прогрессии с практическим содержанием в различных учебных пособиях и интернет-ресурсах.

2. Установить: имеют ли арифметическая и геометрическая прогрессии прикладное значение? Найти примеры применения прогрессий в нашей жизни.

Методы исследования:

1. Анкетирование одноклассников.

2. Анализ школьных учебников математики, математической справочной литературы, материала из Интернета.

Основная часть

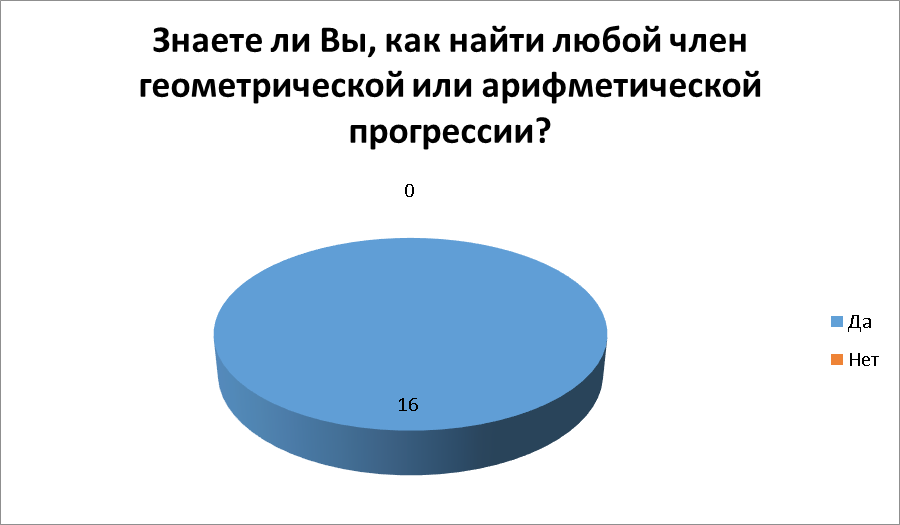
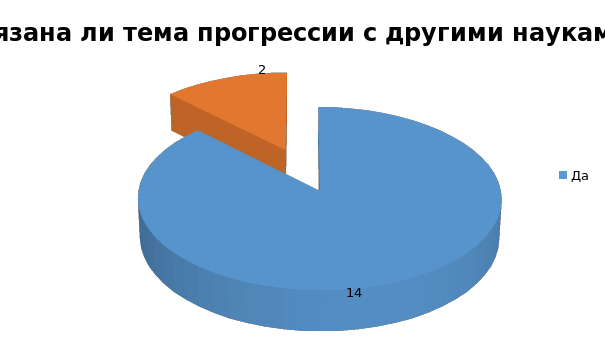
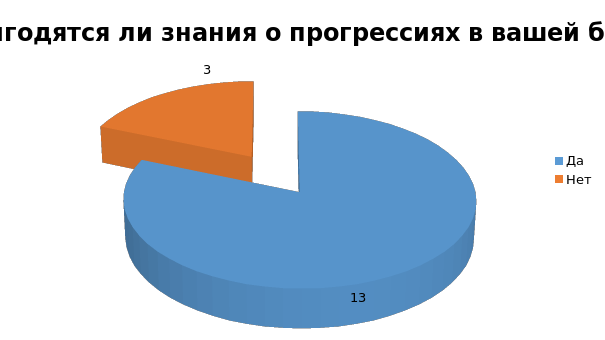
Я провела опрос среди своих одноклассников и выяснила, что формулы нахождения арифметической и геометрической прогрессий знают все. К моему удивлениюбольшинство ребят запомнили с уроков, что прогрессия связанас банковским делом. На вопрос «Ваши родители когда-нибудь брали кредит?» больше половины опрошенныхответили «да», так же из опроса выяснилось, что многие профессии связаны с прогрессиями. Поэтому я считаю свою тему актуальной.

Прогрессии применяются в различных направлениях деятельности человека. Рассмотрим примеры.

Во-первых,прогрессии применяются в медицине.

Задача:Больной принимает лекарство по следующей схеме: в первый день он принимает 5 капель, а в каждый следующий день — на 5 капель больше, чем в предыдущий. Приняв 40 капель, он 3 дня пьет по 40 капель лекарства, а потом ежедневно уменьшает прием на 5 капель, доведя его до 5 капель. Сколько пузырьков лекарства нужно купить больному, если в каждом содержится 20 мл лекарства (что составляет 250 капель)?

Найдя сумму п первых членов арифметической прогрессии, найдете, что вам надо купить 180 капель. Т.е. 2 пузырька лекарства. [Алгебра. 9 класс, в 2ч. Ч.2. Учебник для общеобразовательных учреждений/ Мордкович А.Г., П.В. Семенов , -М.: Мнемозина, 2014, -224с.(с.100)]

Решение. Составим математическую модель задачи:

5, 10, 15,…,40, 40, 40, 35, 30,…,5

а_п=а₁+d(n-1), 40=5+5(п-1), п=8, Sп=((a1+aп)n)/2, S8 =(5+40)·8:2=180,

180 капель больной принимал по схеме в первый период и столько же по второй период. Всего он принял 180+40+180=400(капель), всего больной выпьет 400:250=1,6 (пузырька). Значит, надо купить 2 пузырька лекарства.

Ответ: 2 пузырька.

Прогрессии применяются и в спорте.

Задача:Альпинисты в первый день восхождения поднялись на высоту 1400 м, а затем каждый следующий день они проходи ли на 100 м меньше, чем в предыдущий. За сколько дней они покорили высоту в 5000м?[Задача № 471 Алгебра. 9 класс, в 2ч. Ч.2. Учебник для общеобразовательных учреждений/ Мордкович А.Г., П.В. Семенов , -М.: Мнемозина, 2014, -224с.(с.100)

Дано: a₁=1400; d=-100, S_n=5000. Надо найти n.

Решение: S_n= (2a₁+ d (n-1))n:2;

5000= (2·1400-100 · (n-1)) n:2; Условию задачи удовлетворяет

10000= (2800-100 n+100) n; n=4 ( при n=25 а_n=-1000, но а_n0)

10000= (2900-100 n) n; Значит, альпинисты покорили

100 n2-2900 n+10000=0; высоту за 4 дня.

n2-29 n+100=0; n=25, n=4. Ответ: за 4 дня.

Задача В соревновании по стрельбе за каждый промах в серии из 25 выстрелов стрелок получал штрафные очки: за первый промах — одно штрафное очко, за каждый последующий — на 0,5 очка больше, чем за предыдущий. Сколько раз попал в цель стрелок, получивший 7 штрафных очков?

Решение:

Подсчитаем количество промахов.

- промахов

- не удовлетворяет условию задачи

- попаданий

Ответ: 21 раз попал в цель стрелок.

Прогрессии в литературе.

До изучения прогрессий я никогда бы ни подумала, что они могут присутствовать в таких предметах, как литература.Оказывается, прогрессия наблюдается в размерности стиха. Вот каковы прогрессии в литературе:

«…Не мог он ямба от хорея

Как мы не бились отличить…».

Отличие ямба от хорея состоит в различных расположениях ударных слогов стихотворения.

Ямб – это стихотворный размер с ударением на четных слогах 2; 4; 6; 8;…Номера ударных слогов образуют арифметическую прогрессию с первым членом 2 и разностью прогрессии 2.

Хорей – это стихотворный размер с ударением на нечетныхслогах стиха. Номера ударных слогов образуют арифметическую прогрессию 1; 3; 5; 7;..

Примеры.

Ямб. «Мой дЯдясАмыхчЕстныхпрАвил…», прогрессия 2; 4; 6; 8;…

Хорей. «БУрямглОюнЕбокрОет» А.С. Пушкин, прогрессия 1; 3; 5;7;

[«Сборника старинных занимательных задач по математике» Игнатьева Е.И.]

Арифметическая и геометрическая прогрессии используются в физике для решения задач на равноускоренное движение.

Задача :Поезд, отойдя от станции, равномерно увеличивал скорость на 50 м в мин. Какова была скорость поезда в конце 20 минуты?.[Ю.Н. Макарычев, Н.Г. Миндюк, К.Н. Нешков, С.Б. Суворов. Алгебра 9: учебник для общеобразовательных учреждений под редакцией С.А. Теляковского, 19- е изд.- М:Просвещени, 2017]

Решаем с использованием арифметической прогрессии

Дано: 1 мин: 50 м 2 мин: 50м + 50м 3 мин: 50м + 50м + 50м

Решение:a_n=a₁+d(n-1); a₁=50; d=a₂-a₁=100-50=50; a₂₀=a₁+d(20-1); a₂₀=50+50*19=1000м/мин=1км/мин=60км/ч

Ответ: скорость поезда в конце 20-й минуты 60км/ч

Задача: При свободном падении тело прошло в первую секунду 5 метров, а в каждую следующую на 10 м больше. Найдите глубину шахты, если свободно падающее тело достигло ее дна через 5 секунд после падения.

Решаем с использованием арифметической прогрессии.

Дано: 1с: 5м 2с: 5м + 10м = 15м3с: 15м + 10м = 25м

Глубина шахты равна сумме 5 членов арифметической прогрессии

Найти: S₅-?

Решение:S_n=(a₁+a_n)*n/2; a_n=a₁+d(n-1); a₁=5; d=10; a₅=5+10*(5-1)=45м; h=s₅=(5+45)*5/2=125м

Ответ: глубинашахты 125 м

Прогрессии применяются в строительном деле.

Задание 20 № 506688

Хозяин до­го­во­рил­ся с рабочими, что они ко­па­ют ко­ло­дец на сле­ду­ю­щих условиях: за пер­вый метр он за­пла­тит им 3500 рублей, а за каж­дый сле­ду­ю­щий метр — на 1600 руб­лей больше, чем за предыдущий. Сколь­ко денег хо­зя­ин дол­жен будет за­пла­тить рабочим, если они вы­ко­па­ют ко­ло­дец глу­би­ной 9 метров?

Решение.

Последовательность цен за метр — ариф­ме­ти­че­ская про­грес­сия с пер­вым эле­мен­том a₁=3500и раз­но­стьюd =1600. Сумма n пер­вых эле­мен­тов ариф­ме­ти­че­ской про­грес­сии — S_n=(a₁+a_n)*n/2 . То есть в нашем слу­чае имеемS₉=(a₁+a₉)*9 /2;a₉=3500+1600*8=16300 рублей.S₉=(3500 +16300)*9 /2=89100 рублей.

Ответ:89100 рублей.

Задание 11 № 99579

Задача: Бригада маляров красит забор длиной 240 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 60 метров забора. Определите, сколько дней бригада маляров красила весь забор.

Решение.Пусть бригада в первый день покрасила a₁метров забора, во второй —a₂,….,в последний — a_n метров забора. Тогда a₁+a_n=60м, а заnдней было покрашеноS_n=(a₁+a_n)*n/2=30nметров забора.Поскольку всего было покрашено 240 метров забора, имеем: 30n=240метров, n=8. Таким образом, бригада красила забор в течение 8 дней.

Ответ: 8 дней.

Задание 11 №99580

Задача:Рабочие прокладывают тоннель длиной 500 метров, ежедневно увеличивая норму прокладки на одно и то же число метров. Известно, что за первый день рабочие проложили 3 метра тоннеля. Определите, сколько метров тоннеля проложили рабочие в последний день, если вся работа была выполнена за 10 дней.

Решение.

Пусть рабочие в первый день проложилиa₁метровтоннеля, во второй —a₂,….,в последний — a_n метров тоннеля. Длина тоннеляS_n=(a₁+a_n)*n/2=500 метров.n=10 дней.Тогда в последний день рабочие проложилиa₁₀=2S_n/n-a₁=1000/10-3=97метров.Таким образом, рабочие в последний день проложили 97 метров тоннеля.

Ответ: 97.

Прогрессии и слухи.

Так же я нашла не менее интересную задачу про слухи.Удивительно, как быстро разбегаются по посёлку слухи! Решила придумать свою и предложить её одноклассникам.

Задача: В селе Аладьино 1200 жителей. Приезжий человек из села Красное озеро в 9:00 начинает рассказывать новость 2 людям, стоявшим в очереди у молочной палатки, каждый из них рассказывает в течении получаса новость уже двум своим соседям и т. д. Во сколько эта новость станет известна половине жителей села Аладьино?

Решение: Если слух распространяется по посёлку и далее таким способом, то есть каждый узнавший эту новость успевает в ближайшие полчаса передать её двум согражданам, то осведомление посёлка будет происходить по следующему расписанию:

в 09.00 новость знают 1+2=3(человек);

09.302+2*2=6(человек);

10.006+6*6=42(человек)

10.30 42+42*42=1806(человек)

Ответ: меньше чем через полтора часа.

Выводы

При исследовании задач учебников, сайтов подготовки выпускников к экзаменам я убедилась, что прогрессии имеют большое прикладное значение.

Решая задачи, я убедилась в том, что прогрессии используются в различных науках, и многих профессиях.

Я приобрела навык решения задач на арифметическую и геометрическую прогрессии.

Много экономических задач связанных с прогрессией. Этим я буду заниматься в следующем году.

Литература, интернет-ресурсы:

• Аксенова М.Д. Энциклопедия для детей Т.11. Математика гл. ред. Аксенова М.Д. – М.: Аванта «+», 1998.

• Пичугин Л.Ф. За страницами учебника алгебры. – М: Просвещение, 1990

• Шевелева Н.В., Корешкова Т.А., Мирошин В.В. Математика (Алгебра, элементы статистики и теории вероятностей). 9 класс/ М.: Национальное образование, 2011

• Алгебра. 9 класс, в 2ч. Ч.2. Учебник для общеобразовательных учреждений/ Мордкович А.Г., П.В. Семенов , -М.: Мнемозина, 2014, -224с.(с.100)]

• Ю.Н. Макарычев, Н.Г. Миндюк, К.Н. Нешков, С.Б. Суворов. Алгебра 9: учебник для общеобразовательных учреждений под редакцией С.А. Теляковского, 19- е изд.- М:Просвещени, 2017

• «Сборника старинных занимательных задач по математике» Игнатьева Е.И.

• Кордемский Б.А. Удивительный мир чисел /Б. А. Кордемский,А.А.Ахадов- М.:Просвещение, 1986

• https://math-ege.sdamgia.ru/test?theme=89

• https://nsportal.ru/

• http://www.5egena5.ru/zadachi-po-matematike-9klass.