Россия, п. Заполярный
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 04.12.2023 10:50
Колесник Марина Анатольевна
Репетитор по математике
58 лет
47 159
361 
Местоположение
Специализация
Линейная функция и её график
Категория:
Алгебра
07.02.2018 11:15
Просмотр содержимого документа
«Линейная функция и её график»
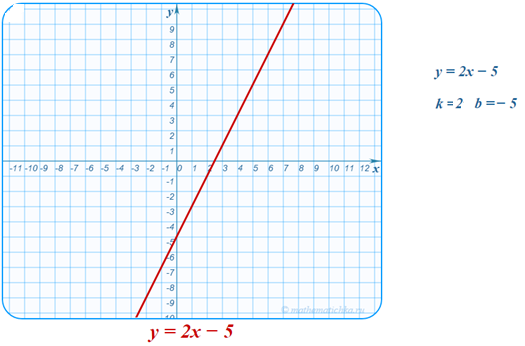
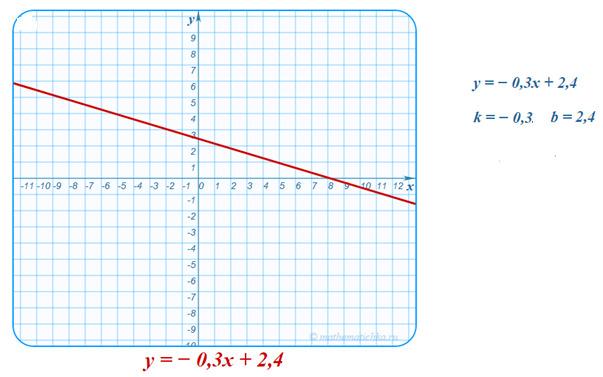
Линейной функцией называется функция, заданная формулой y = kx + b, где k и b - любые действительные числа.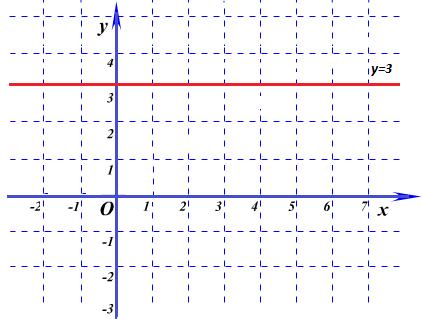
Если k = 0, то функция y = b называется постоянной. Её графиком, является прямая, параллельная оси Ox, проходящая через
точку (0; b)
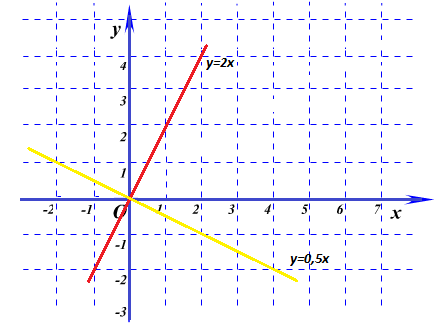
Если b = 0, то формула y = kx задаёт прямо пропорциональную зависимость. Графиком такой функции является прямая, проходящая через начало координат и точку (xo;yo). Если k0, то прямая составляет с положительным направлением оси Ox острый угол. Если k, то прямая составляет с положительным направлением оси Ox тупой угол.
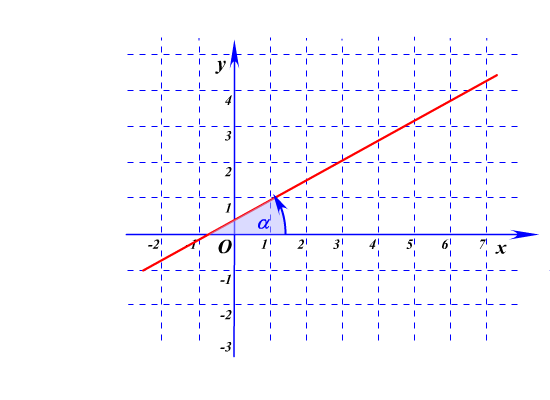
Графиком линейной функции является прямая, проходящая через точки (0;b) и (xo;yo).
Число k называется угловым коэффициентом прямой, оно равно тангенсу угла между прямой и положительным направлением оси Ox. k=tgα
Свойства линейной функции при k ≠ 0, b ≠ 0.
1) Область определения функции - множество всех действительных чисел: R или (−∞; ∞).
2) Функция y = kx + b ни чётна, ни нечётна.
3) При k 0 функция монотонно возрастает, а при k
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
