Нестандартный способ решения логарифмического неравенства.
Метод рационализации
Составитель разработки -Бибаева А.М.
Учитель математики МБОУСОШ №3 г.Беслан
«Стандартный» метод решения логарифмических неравенств
Рассмотрим традиционный метод решения логарифмического неравенства на конкретном примере.
| Пример 1. Решить логарифмическое неравенство: 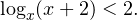 |
Вне зависимости от того, каким методом вы решаете то или иное логарифмическое неравенство, начинать всегда нужно с области допустимых значений. Основание логарифма должно быть положительным и не равным 1, а выражение, стоящее под знаком логарифма, — положительным. То есть область допустимых значений в нашем примере определяется следующей системой:

Видно, что решением данной системы является промежуток:  .
.
Теперь, используя свойства логарифмов, представим двойку справа в виде логарифма с основанием 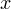 . Тогда неравенства примет вид:
. Тогда неравенства примет вид:
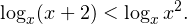
Далее решение неравенства разбивается на два случая:
1) если 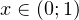 . В этом случае в основаниях логарифмов стоят одинаковые числа из интервала
. В этом случае в основаниях логарифмов стоят одинаковые числа из интервала  . Значит, соответствующие логарифмические функции являются убывающими. Поэтому, опуская знаки логарифмов, нам нужно изменить знак неравенства на обратный. В результате в этом случае приходим к следующему неравенству:
. Значит, соответствующие логарифмические функции являются убывающими. Поэтому, опуская знаки логарифмов, нам нужно изменить знак неравенства на обратный. В результате в этом случае приходим к следующему неравенству:
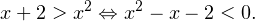
Изобразим соответствующую параболу, ветви которой направлены вверх, пересекающую ось OX в двух точках:  и
и  , являющихся корнями квадратного трёхчлена
, являющихся корнями квадратного трёхчлена  :
:

Тогда с учётом рассматриваемого ограничения на 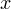 получаем для этого случая
получаем для этого случая 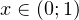 .
.
2) рассмотрим теперь случай, когда  . В этом случае оба логарифма будут возрастающими, поэтому после ухода от знаков логарифма, знак неравенства останется прежним. То есть в этом случае исходное логарифмическое неравенство можно заменить следующим:
. В этом случае оба логарифма будут возрастающими, поэтому после ухода от знаков логарифма, знак неравенства останется прежним. То есть в этом случае исходное логарифмическое неравенство можно заменить следующим:
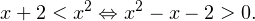
В учётом ограничения на 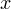 решение этого неравенства можно проиллюстрировать на числовой прямой следующим образом:
решение этого неравенства можно проиллюстрировать на числовой прямой следующим образом:

То есть решение в данном случае имеет вид: 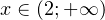 .
.
Объединяя решения, полученные в пунктах а) и б), приходим к окончательному ответу, который имеет вид:  .
.
Как известно, ЕГЭ по математике длится 235 минут, и чтобы распределить это время рационально на все задания, не помешало бы узнать короткие пути решения той или иной задачи. Так, на задача №14 оцениваемое в 2 балла, рекомендовано 30 минут (при условии, что ученик намерен решать все задания). Если проводить решение согласно всем известному методу интервалов, то, возможно, вы потратите все отведенное на него время. Существует ли такой метод решения неравенств, при котором мы сможем упростить наши вычисления, тем самым сохранив время?
Вернемся к нашему неравенству. Описанный в предыдущем параграфе способ является правильным, но при этом чрезвычайно неудобным. Как видите, приходится рассматривать два отдельных случая, что существенно повышает вероятность совершения ошибки. Гораздо проще поступить следующим образом. Перепишем исходное логарифмическое неравенства в виде:
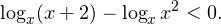
А дальше, в области допустимых значений, то есть при  (это мы установили выше), данное неравенство можно заменить следующим равносильным ему неравенством:
(это мы установили выше), данное неравенство можно заменить следующим равносильным ему неравенством:
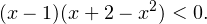
Ну действительно, если  , то первая скобка положительна, и на неё можно разделить, не меняя при этом знак неравенства. Если же
, то первая скобка положительна, и на неё можно разделить, не меняя при этом знак неравенства. Если же  , то первая скобка отрицательна, и при делении на неё, знак неравенства изменится на противоположный.
, то первая скобка отрицательна, и при делении на неё, знак неравенства изменится на противоположный.
То есть мы получили ровно то же самое, что имели в предыдущем пункте. Но при этом нет необходимости рассматривать два случая. Всё решается в рамках одного единственного неравенства. И хотя этот способ не избавляет нас от необходимости определения области допустимых значений, он всё равно приводит к существенному упрощению решения задачи.
Решаем полученное неравенство методом интервалов. Для этого поменяем знаки во второй скобке, разделим обе части неравенства на -1, поменяв знак неравенства:
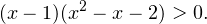
Теперь разложим выражение во вторых скобках на множители:

Изобразим на числовой прямой множество решений полученного неравенства (стрелкой обозначена область допустимых значений исходного логарифмического неравенства):
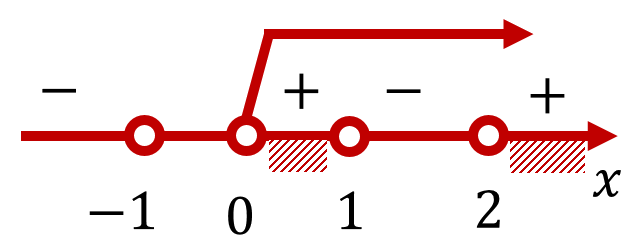
В результате получаем тот же результат, что и в предыдущем параграфе:
 .
.
Это метод рационализации (оптимизации, декомпозиции, замены множителей, замены функций, обобщенный метод интервалов, правило знаков)
Теоретическое обоснование метода
Часто, при решении логарифмических неравенств, встречаются задачи с переменным основанием логарифма. Так, неравенство вида

является стандартным школьным неравенством. Как правило, для его решения применяется переход к равносильной совокупности систем:

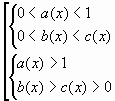
Недостатком данного метода является необходимость решения семи неравенств, не считая двух систем и одной совокупности. Уже при данных квадратичных функциях решение совокупности может потребовать много времени. Можно предложить альтернативный, менее трудоемкий метод решения этого стандартного неравенства. Это метод рационализации неравенств, известный в математической литературе под названием декомпозиции.
Метод декомпозиции
Метод декомпозиции заключается в замене сложного выражения F(x) на более простое выражение G(x), при которой неравенство G(x)^0 равносильно неравенству F(x)^0 в области определения F(x).
f, g, h – выражения с переменной х, a – фиксированное число или функция ( а0, a≠1).
|
| Выражение F | Выражение G |
| 1 | 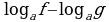
| 
|
|
| 
| 
|
|
| 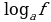
| 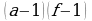
|
| 2 | 
| 
|
|
| 
| 
|
|
| 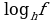
| 
|
| 3 | 
| 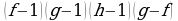
|
|
| 
| 
|
|
| 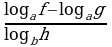
| 
|
| 4 | 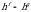
| 
|
|
| 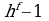
| 
|
|
| 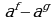
| 
|
| 5 | 
| 
|
|
| 
| 
|
| 6 | 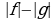
| 
|
Из данных выражений можно вывести некоторые следствия (с учетом области определения):

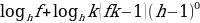
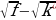 0
0 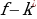 0
0
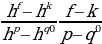
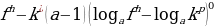
В указанных равносильных переходах символ ^ заменяет один из знаков неравенств: ,
Для решения:
1) Рассмотрим пример решения логарифмического неравенства двумя методами

1. Метод интервалов

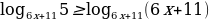






-11/6
-5/3
////////////////////////////
x
О.Д.З. 

a) 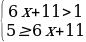 b)
b)

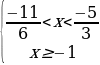






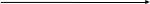





-5/3
-11/6
////////////////
x
//////////////////
x








x
///////
x
//////////////////////
-1



-1
-5/3

Нет решений






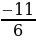
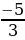
x



/////////////////////






-1
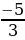
x

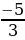
Ответ: (  ;
; 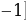
2. Метод декомпозиции (рационализации)

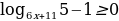
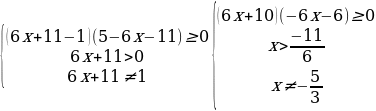



//////////////////////////////////////////////////////////////////
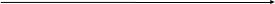







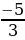
x
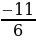

//////////////////////////////////////////////////////////////////





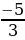
-1
x

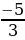
Ответ: ( ; 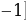
2. Пример

1) 
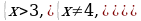
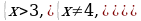

2)  ,
,
 ,
,
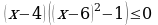 ,
,
 ,
, 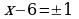 ,
,
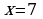 ,
, 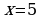
 ,
,
 ,
,  ;
;

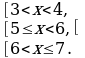
 U
U 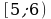 U
U 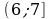 .
.
Ответ.  ,
, 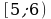 ,
, 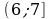 .
.
3) Пример

Решение.
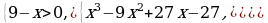
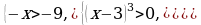
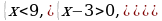


 ,
,
 ,
,
 ,
,
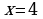 ,
, 
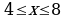 ;
;
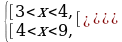
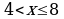 ,
, 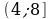
Ответ. 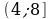
4. Пример.
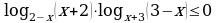
1) 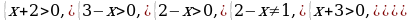



2) 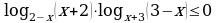 ,
,
 ,
,
 ,
,
 ,
, 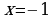 ,
,  ,
,  ,
,
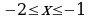 ,
, 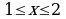 .
.
3)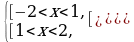

 U
U 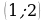 .
.
Ответ.  ,
, 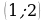 .
.
5)log12x2-41+35(3 – x) ≥ log2x2-5x+3(3- x).
Решение. Запишем неравенство в виде log12x2-41+35(3 – x) - log2x2-5x+3(3- x) ≥ 0 и заменим его равносильной системой, используя метод рационализации
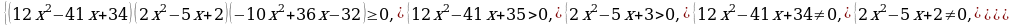
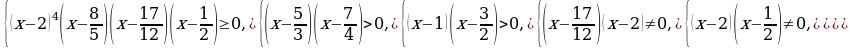
Для решения первых трёх неравенств системы используем метод интервалов.
Ответ: 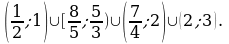
6) 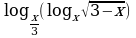 ≥ 0.
≥ 0.
Решение. Заменим данное неравенство равносильной системой, используя метод рационализации



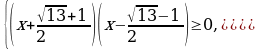
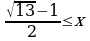
При решении неравенства (х – 1)(х – 2) x x 0, x ≠ 1. Условие 1 x позволяет исключить множитель x – 1 0 в первом неравенстве системы.
Ответ: 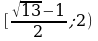 .
.
Дополнительно

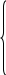
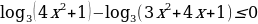
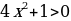




 [0; 4]
[0; 4]



///////////////////////////////////////////////////////////////
///////////////////////////////////////////////////////////////
х
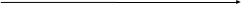






-1/3
-1




///////////////////////////////////////////////////////////////
х
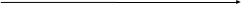


4
0
Ответ: [0; 4]
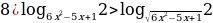
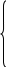

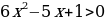
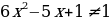
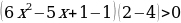
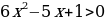 -2
-2 
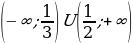






Ответ: 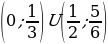

Решение:
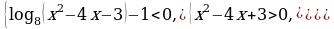
Ответ: (-1;1) U (3;5)
10) Решите неравенство log 2x+3 x2
 Решение. Запишем неравенство в виде log2x+3x2 – 1
Решение. Запишем неравенство в виде log2x+3x2 – 1
(2x + 2)(x2 – 2x – 3)
2x + 3 0
x ≠ 0

(x + 1)(x + 1)(x – 3)
x 1,5
x ≠ 0
Ответ: (-1.5; -1)  (-1; 0)
(-1; 0)  (0; 3).
(0; 3).
11) 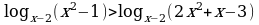 .
.
Решение. Получим следующую систему неравенств:

Решая первые четыре неравенства, практически находим ОДЗ исходного неравенства:

Откуда: 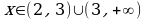 .
.
Решим теперь пятое неравенство системы. После элементарных преобразований получим неравенство
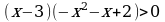 .
.
Умножим второй сомножитель на -1 и поменяем знак неравенства:
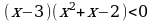 .
.
Нетрудно заметить, что корнями второго множителя в этом неравенстве являются числа 1 и -2. Поэтому, раскладывая второй множитель на одночлены первого порядка, получаем:
 .
.
Это неравенство легко решить методом интервалов:  .
.
С учетом найденного ранее ОДЗ, получаем окончательный ответ.
Ответ:  .
.
12)

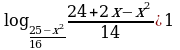
Решение.



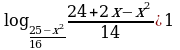 ,
,
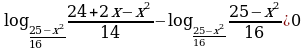 ,
,
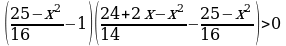 ,
,
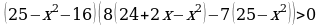 ,
,
 ,
,
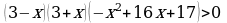 ,
,
 ,
,
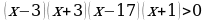 ,
,
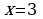 ,
, 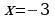 ,
, 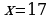 ,
, 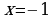
 ,
,  ,
,  .
.

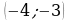 ,
,  .
.
Ответ. 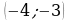 ,
,  .
.
13) 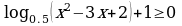
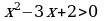
 ,
, 
 ,
, 
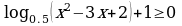 ,
,
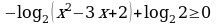 ,
,
 ,
,
 ,
,
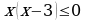 ,
,
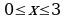 .
.
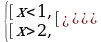
 ,
, 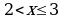 .
.
Ответ.  .
.
Дополнительно для самостоятельного решения:
 . Ответ.
. Ответ.  .
.
 . Ответ.
. Ответ. 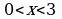 ,
, 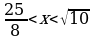 .
.
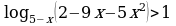 . Ответ.
. Ответ. 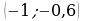
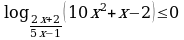 . Ответ.
. Ответ. 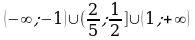 .
.
 . Ответ.
. Ответ. 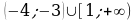 .
.
Комментарий.
Стандартные ошибки, которые допускают учащиеся при использовании метода рационализации, заключаются в следующем:
а) проводят рационализацию без учета области определения данного неравенства;
б) применяют метод рационализации к неравенствам, не приведенным к стандартному виду F(x) ˅ 0;
в) формально применяют метод рационализации к выражениям вида
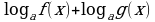 , заменяя на выражение
, заменяя на выражение 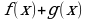 ;
;
г) подменяют формулировку «о совпадении знаков выражений для каждого
допустимого значения х» на неверную формулировку «о совпадении значений
выражений для каждого допустимого значения х».
Для работы с учениками:
Детям нужно рекомендовать использование метода рационализации в логарифмических неравенствах, когда неизвестное находится в основании степени.
Для отработки навыка решения предлагать решение в 3действия:
Найти область определения неравенства.
Использование замены функций по формулам рационализации.
Решить систему всех полученных условий.
Список литературы:
Семенов А.Л., Ященко И.В. Математика 2021. 30 вариантов. М.: Экзамен, 2021
Методы решения неравенств с одной переменной. www.alexlarin.net
Лысенко Ф.Ф., Кулабухова С.Ю. Математика. Подготовка к ЕГЭ – 2021.
1










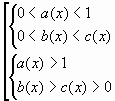
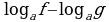



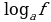
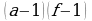




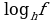


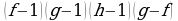


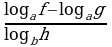

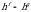
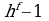

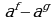





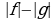


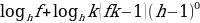
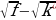 0
0 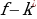 0
0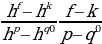
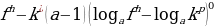

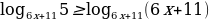

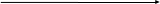






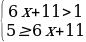 b)
b)

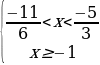

















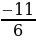
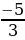





 ;
; 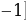
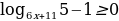
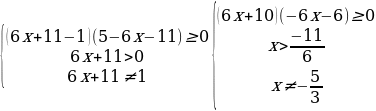



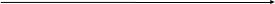






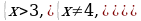

 ,
,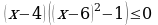 ,
, ,
, 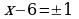 ,
,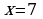 ,
, 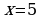
 ,
, ,
,  ;
;
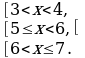
 U
U 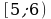 U
U 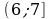 .
.
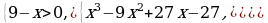
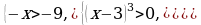
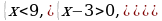


 ,
, ,
,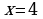 ,
, 
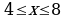 ;
;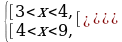
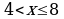 ,
, 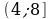
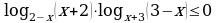
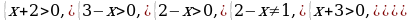



 ,
, ,
, ,
, 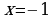 ,
,  ,
,  ,
,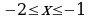 ,
, 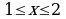 .
.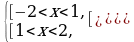

 U
U 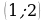 .
.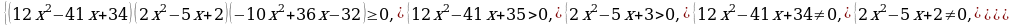
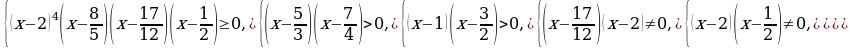
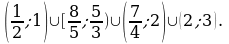
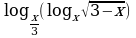 ≥ 0.
≥ 0.


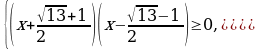
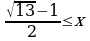
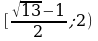 .
.

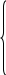
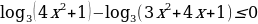
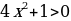



 [0; 4]
[0; 4] 








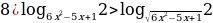

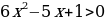
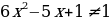
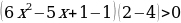

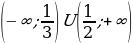




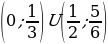

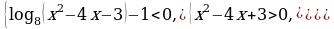
 Решение. Запишем неравенство в виде log2x+3x2 – 1
Решение. Запишем неравенство в виде log2x+3x2 – 1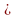 (-1; 0)
(-1; 0) 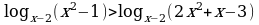 .
.

 .
.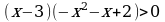 .
.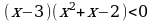 .
. .
. .
. .
.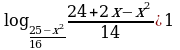



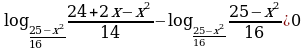 ,
,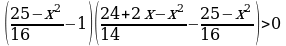 ,
,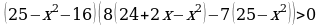 ,
, ,
,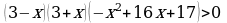 ,
, ,
,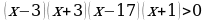 ,
,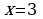 ,
, 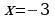 ,
, 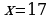 ,
,  ,
,  ,
,  .
.
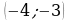 ,
,  .
.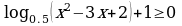
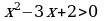
 ,
, 
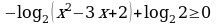 ,
, ,
, ,
,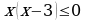 ,
,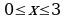 .
.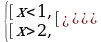
 ,
, 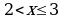 .
. .
. . Ответ.
. Ответ.  .
. . Ответ.
. Ответ. 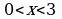 ,
, 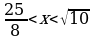 .
.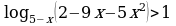 . Ответ.
. Ответ. 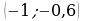
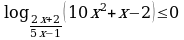 . Ответ.
. Ответ. 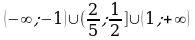 .
. . Ответ.
. Ответ. 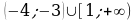 .
.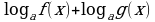 , заменяя на выражение
, заменяя на выражение 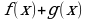 ;
;

















