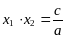ТЕМЫ ДИКТАНТОВ (9 класс)
| № п/п | Тема | Назначение | Количество вопросов |
| 1 | Функции и их свойства | т | 9 |
| 2 | Квадратный трёхчлен | т, п | 8 |
| 3 | Квадратичная функция и её график | т, п | 11 |
| 4 | Квадратичная функция | словарный | 12 |
| 5 | Уравнения и системы уравнений | т, п | 8 |
| 6 | Последовательности | т, п | 8 |
| 7 | Арифметическая прогрессия | т, п | 10 |
| 8 | Геометрическая прогрессия | т, п | 10 |
| 9 | Последовательности | словарный | 7 |
| 10 | Чётные и нечётные функции | т, п | 8 |
| 11 | Степенная функция | т, п | 10 |
| 12 | Определение корня n-й степени | п, т | 9 |
| 13 | Свойства корня n-й степени | п, т | 10 |
| 14 | Степень с дробным показателем | п, т | 9 |
П р и м е ч а н и е: (т – теоретические вопросы, п – практические вопросы, порядок букв указывает, каких вопросов больше).
Функции и их свойства
Вариант 1
1. Дайте определение функции.
2. Что называется областью значений функции?
3. Что представляет собой график линейной функции?
4. Как называется график обратной пропорциональности?
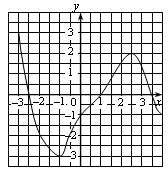
5. Используя рисунок, укажите нули функции.
6. Используя рисунок, укажите промежутки, в которых функция принимает положительные значения.
7. Дайте определение функции, убывающей в промежутке.
8. Назовите промежутки возрастания функции, график которой изображён на рисунке.
9. Приведите пример возрастающей линейной функции.
Вариант 2
1. Что называется графиком функции?
2. Что называется областью определения функции?
3. Что представляет собой график прямой пропорциональности?
4. Как называется график квадратичной функции?
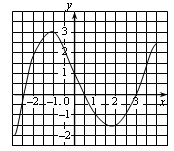
5. Используя рисунок, укажите нули функции.
6. Используя рисунок, укажите промежутки, в которых функция принимает отрицательные значения.
7. Дайте определение функции, возрастающей в промежутке.
8. Назовите промежутки убывания функции, график которой изображён на рисунке.
9. Приведите пример убывающей линейной функции.
Ответы:
| Вариант 1 | Вариант 2 |
| 1. Функцией называют такую зависимость переменной у от переменной х, при которой каждому значению переменной х соответствует единственное значение переменной у | 1. Графиком функции называют множество точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции |
| 2. Все значения, которые принимает зависимая переменная, образуют область значений функции | 2. Все значения независимой переменной образуют область определения функции |
| 3. Прямая | 3. Прямая, проходящая через начало координат |
| 4. Гипербола | 4. Парабола |
| 5. – 2,5; 0,5; 3 | 5. – 2,5; 1; 3,5 |
| 6. (– 2,5; 0,5), (3; 4) | 6. (– 2,5; 1), (3,5; 4) |
| 7. Функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции | 7. Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции |
| 8.  | 8.  |
| 9. у = 4х – 1 | 9. у = –2х + 3 |
Квадратный трёхчлен
Вариант 1
1. Дайте определение квадратного трёхчлена.
2. Чему равно произведение корней квадратного трёхчлена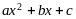 ?
?
3. Когда квадратный трёхчлен не имеет корней?
4. Разложите на множители 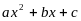 , если известно, что
, если известно, что  и
и 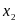 – корни квадратного трёхчлена.
– корни квадратного трёхчлена.
5. Выделите квадрат двучлена из квадратного трёхчлена: 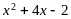 .
.
6. Разложите квадратный трёхчлен  на множители, если его корни 3 и – 2.
на множители, если его корни 3 и – 2.
7. Какие корни имеет квадратный трёхчлен, если его можно представить в виде произведения 4(х – 1)(х + 7)?
8. Запишите квадратный трёхчлен, если первый коэффициент равен 1, а его корни –1 и 2.
Вариант 2
1. Что называется корнем квадратного трёхчлена?
2. Чему равна сумма корней квадратного трёхчлена 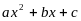 ?
?
3. Когда квадратный трёхчлен имеет два корня?
4. Когда квадратный трёхчлен нельзя разложить на множители?
5. Выделите квадрат двучлена из квадратного трёхчлена: 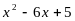 .
.
6. Разложите квадратный трёхчлен 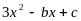 на множители, если его корни –4 и 5.
на множители, если его корни –4 и 5.
7. Какие корни имеет квадратный трёхчлен, если его можно представить в виде произведения 6(х + 2)(х – 9)?
8. Запишите квадратный трёхчлен, если первый коэффициент равен 1, а его корни –2 и 3.
Ответы:
| Вариант 1 | Вариант 2 |
| 1. Квадратным трёхчленом называется многочлен вида 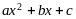 , где х – переменная, а, b и c – некоторые числа, причём , где х – переменная, а, b и c – некоторые числа, причём 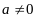 | 1. Корнем квадратного трёхчлена называется значение переменной, при котором значение этого трёхчлена равно нулю |
| 2. 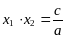 | 2.  |
| 3. Если его дискриминант меньше нуля | 3. Если его дискриминант больше нуля |
| 4. 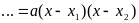 | 4. Если его дискриминант меньше нуля |
| 5. х2 + 4х + 4 –6 = (х + 2)2 – 6 | 5. х2 – 6х + 9 –4 = (х – 3)2 – 4 |
| 6. 5 (х – 3)(х + 2) | 6. 3 (х + 4)(х – 5) |
| 7. х1 = 1; х2 = –7 | 7. х1 = –2; х2 = 9 |
| 8. (х + 1)(х – 2) = х2 – х – 2 | 8. (х + 2)(х – 3) = х2 – х – 6 |
Квадратичная функция и её график
Вариант 1
1. Запишите формулу, задающую квадратичную функцию.
2. Какое значение принимает функция 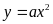 , если аргумент равен нулю?
, если аргумент равен нулю?
3. В какой части координатной плоскости расположен график функции  при а 0?
при а 0?
4. Запишите промежуток убывания функции 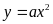 при а 0.
при а 0.
5. Какое наименьшее значение принимает функция  при а 0?
при а 0?
6. На каком промежутке возрастает функция  при а 0?
при а 0?
7. Какое наибольшее значение принимает функция  при а 0?
при а 0?
8. С помощью какого преобразования можно из графика функции 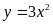 получить график функции
получить график функции  ?
?
9. Какой формулой задаётся функция, график которой получен с помощью параллельного переноса графика функции у = 2х2 по оси Оу на 5 единиц вниз?
10. Как из графика функции  можно получить график функции
можно получить график функции  ?
?
11. Найдите абсциссу вершины параболы функции у = –2х2 – 4х –3.
Вариант 2
1. Как называется график квадратичной функции?
2. В какой части координатной плоскости расположен график функции 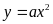 при а 0?
при а 0?
3. Чему равен аргумент, если значение функции  равно нулю?
равно нулю?
4. Какое наибольшее значение принимает функция  при а 0?
при а 0?
5. Запишите промежуток возрастания функции  при а 0?
при а 0?
6. Какое наименьшее значение принимает функция  при а 0?
при а 0?
7. На каком промежутке убывает функция  при а 0?
при а 0?
8. С помощью какого преобразования можно из графика функции  получить график функции
получить график функции  ?
?
9. Какой формулой задаётся функция, график которой получен с помощью параллельного переноса графика функции у = 3х2 по оси Ох на 4 единицы вправо?
10. По какой формуле находят абсциссу вершины графика квадратичной функции?
11. Найдите абсциссу вершины параболы функции у = 2х2 –10х + 5.
Ответы:
| Вариант 1 | Вариант 2 |
| 1.  | 1. Парабола |
| 2. у = 0 | 2. В верхней полуплоскости |
| 3. В нижней полуплоскости | 3. х = 0 |
| 4.  | 4. Наибольшего значения функция не имеет |
| 5. Наименьшего значения функция не имеет | 5.  |
| 6.  | 6. у = 0 |
| 7. у = 0 | 7.  |
| 8. Параллельный перенос по оси Ох влево на 2 единицы | 8. Параллельный перенос по оси Оу вверх на 3 единицы |
| 9. у = 2х2 – 5 | 9. у = 3(х –4)2 |
| 10. Параллельный перенос по оси Ох на m единиц и n единиц вверх по оси Оу | 10.  |
| 11. х = –1 | 11. х = 2,5 |
Квадратичная функция
Запишите математические термины:
| Вариант 1 | Вариант 2 |
| 1. Зависимость. | 1. Переменная. |
| 2. Аргумент. | 2. Независимая. |
| 3. Область определения. | 3. Множество значений. |
| 4. Абсцисса. | 4. Ордината. |
| 5. Координатная плоскость. | 5. Соответствующие значения. |
| 6. Возрастающая. | 6. Убывающая. |
| 7. Трёхчлен. | 7. Дискриминант. |
| 8. Разложение. | 8. Множитель. |
| 9. Сжатие. | 9. Растяжение. |
| 10. Вершина. | 10. Парабола. |
| 11. Квадратичная функция. | 11. Параллельный перенос. |
| 12. Решение неравенства. | 12. Метод интервалов. |
Уравнения и системы уравнений
Вариант 1
1. Какое уравнение с одной переменной называется целым?
2. Запишите пример целого уравнения с одной переменной второй степени.
3. Сколько корней может иметь уравнение с одной переменной третьей степени?
4. С помощью какого способа решается биквадратное уравнение?
5. Запишите пример биквадратного уравнения.
6. Дайте определение графика уравнения с двумя переменными.
7. Запишите пример уравнения третьей степени с двумя переменными.
8. Определите степень уравнения: 2х2у + 3ху3 – 1 = 0.
Вариант 2
1. Как найти степень целого уравнения?
2. Сколько корней может иметь уравнение с одной переменной второй степени?
3. Запишите пример целого уравнения с одной переменной третьей степени.
4. Какое уравнение с одной переменной называется биквадратным?
5. Сколько точек пересечения с осью Ох может иметь график функции у = 2х4 + 3х2 – 1?
6. Какие способы решения системы двух уравнений с двумя переменными известны?
7. Запишите пример уравнения второй степени с двумя переменными.
8. Определите степень уравнения: 4х3у2 – 2ху = 0.
Ответы:
| Вариант 1 | Вариант 2 |
| 1. Целым уравнением называется уравнение, у которого левая и правая части являются целыми выражениями | 1. Степенью целого уравнения называют степень равносильного ему уравнения вида Р(х) = 0, Р(х) – многочлен стандартного вида |
| 2. х2 – 2 х = 0 | 2. Не более двух корней |
| 3. Не более трёх корней | 3. у3 + 2у – 1 = 0 |
| 4. Способ подстановки | 4.  |
| 5. 2х4 + 3х2 – 1 = 0 | 5. Не более четырёх точек |
| 6. Графиком уравнения с двумя переменными называется множество точек координатной плоскости, координаты которых обращают уравнение в верное равенство | 6. Графический способ, способ подстановки, способ сложения |
| 7. 3х3 + 2х2 – х = 5 | 7. х2 – 2у = 3 |
| 8. 4 | 8. 5 |
Последовательности
Вариант 1
1. Приведите пример последовательности, заданной формулой n-го члена.
2. Запишите шесть членов последовательности чисел, кратных числу 3.
3. Является ли конечной или бесконечной последовательность чисел, кратных 10?
4. Перечислите члены последовательности, заключенные между у29 и у32.
5. Сколько членов последовательности (хn) расположены между хn–2 и хn+3?
6. Последовательность задана формулой  . Запишите, чему равен её пятый член.
. Запишите, чему равен её пятый член.
7. Запишите последний член последовательности двухзначных чётных чисел.
8. Выпишите первые пять членов последовательности (сn), если с1 = 2 и сn = сn–1 – 3.
Вариант 2
1. Приведите пример последовательности, заданной рекуррентной формулой.
2. Запишите шесть членов последовательности чисел, кратных числу 5.
3. Является ли конечной или бесконечной последовательность чисел, которые являются делителями 3600?
4. Перечислите члены последовательности, заключенные между х33 и х37.
5. Сколько членов последовательности (сn) расположены между сn–1 и сn+5?
6. Последовательность задана формулой  . Запишите, чему равен её третий член.
. Запишите, чему равен её третий член.
7. Запишите последний член последовательности трёхзначных нечётных чисел.
8. Выпишите первые пять членов последовательности (сn), если х1 = –5 и хn = хn–1 +2.
Ответы:
| Вариант 1 | Вариант 2 |
| 1.  | 1.  |
| 2. 3; 6; 9; 12; 15; 18. | 2. 5; 10; 15; 20; 25. |
| 3. Бесконечная. | 3. Конечная. |
| 4. у30, у31. | 4. х34, х35, х36. |
| 5. 4 | 5. 5 |
| 6.  . . | 6.  . . |
| 7. 98 | 7. 999 |
| 8. 2; –1; – 4; –7; –10. | 8. – 5; –3; –1; 1; 3. |
Арифметическая прогрессия
Вариант 1
1. Запишите определение арифметической прогрессии.
2. Приведите пример убывающей арифметической прогрессии.
3. Является ли последовательность чётных чисел арифметической прогрессией?
4. Является ли арифметической прогрессией последовательность  , заданная формулой
, заданная формулой  ?
?
5. Вставьте пропущенный член арифметической прогрессии: 6; … ; 14; 18; …
6. Найдите разность арифметической прогрессии: 6,5; 7,3; 8,1; …
7. Какой формулой может быть задана арифметическая прогрессия?
8. Найдите десятый член арифметической прогрессии, если её первый член равен 1, а разность равна 4.
9. Запишите формулу суммы п первых членов арифметической прогрессии для случая, когда известны первый и п-й члены прогрессии.
10. Запишите формулу, выражающую свойство арифметической прогрессии: “каждый член арифметической прогрессии, начиная со второго, является средним арифметическим предыдущего и последующего членов”.
Вариант 2
1. Дайте определение разности арифметической прогрессии.
2. Приведите пример возрастающей арифметической прогрессии.
3. Является ли последовательность простых чисел арифметической прогрессией?
4. Является ли арифметической прогрессией последовательность  , заданная формулой
, заданная формулой  ?
?
5. Вставьте пропущенный член арифметической прогрессии: 7; … ; 17; 23; …
6. Найдите разность арифметической прогрессии: 4; 2,5; 1; …
7. Запишите формулу п-го члена арифметической прогрессии.
8. Найдите восьмой член арифметической прогрессии, если её первый член равен 2, а разность равна 5.
9. Запишите формулу суммы п первых членов арифметической прогрессии для случая, когда известны первый член и разность прогрессии.
10. Запишите формулу, выражающую свойство арифметической прогрессии: “суммы членов арифметической прогрессии, равноудалённых от середины, равны”.
Ответы:
| Вариант 1 | Вариант 2 |
| 1. Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом | 1. Разностью арифметической прогрессии называется разность между последующим и предыдущим членами прогрессии. Обозначается d |
| 2. 10; 7; 4; 1; … | 2. 5; 9; 13;… |
| 3. Да | 3. Нет |
| 4. Нет | 4. Да |
| 5. 10 | 5. 13 |
| 6. d = 0,8 | 6. d = –1 ,5 |
| 7.  | 7.  |
| 8. 37 | 8. 37 |
| 9. | 9. |
| 10.  | 10.  |
Геометрическая прогрессия
Вариант 1
1. Чему равен знаменатель геометрической прогрессии?
2. Приведите пример возрастающей геометрической прогрессии.
3. Является ли последовательность степеней числа 2 геометрической прогрессией?
4. Вставьте пропущенный член геометрической прогрессии: 3; … ; 27; 81;…
5. Первый член геометрической прогрессии 80, знаменатель 0,5. Запишите следующие четыре члена прогрессии.
6. Первый член геометрической прогрессии 5, второй 2. Найдите знаменатель прогрессии.
7. Запишите формулу п-го члена геометрической прогрессии.
8. Найдите четвертый член геометрической прогрессии, если её первый член равен 1, а знаменатель –2.
9. Запишите формулу суммы п первых членов геометрической прогрессии для случая, когда известны первый член и знаменатель прогрессии.
10. Запишите формулу, выражающую свойство: “произведения членов геометрической прогрессии, равноудалённых от середины, равны”.
Вариант 2
1. Запишите определение геометрической прогрессии.
2. Приведите пример убывающей прогрессии.
3. Является ли последовательность нечётных чисел геометрической прогрессией?
4. Вставьте пропущенный член геометрической прогрессии: 
5. Первый член геометрической прогрессии – 3, знаменатель – 2. Запишите следующие четыре члена прогрессии.
6. Первый член геометрической прогрессии 2, второй – 8. Найдите знаменатель прогрессии.
7. Найдите шестой член геометрической прогрессии, если её первый член равен 3, а знаменатель 2.
8. Запишите формулу, с помощью которой можно найти первый член геометрической прогрессии, зная п-й член и знаменатель.
9. Запишите формулу суммы п первых членов геометрической прогрессии для случая, когда известны первый и п-й члены прогрессии.
10. Запишите формулу, выражающую свойство: “Любой член геометрической прогрессии, начиная со второго, является средним пропорциональным предыдущего и последующего членов”.
Ответы:
| Вариант 1 | Вариант 2 |
| 1. Чтобы найти знаменатель геометрической прогрессии, необходимо последующий член разделить на предыдущий:  | 1. Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число. |
| 2. 2; 6; 18; 2. | 2. 64; 32; 16; … |
| 3. Да | 3. Нет |
| 4. 9 | 4.  |
| 5. 40; 20; 10; 5 | 5. –6; 12; –24; 48 |
| 6. 0,4 | 6. – 4 |
| 7.  | 7. 96 |
| 8. –8 | 8.  |
| 9.  , где , где  | 9.  , где , где  |
| 10.  | 10.  |
Последовательности
Запишите математические термины:
| Вариант 1 | Вариант 2 |
| 1. Последовательность. | 1. Прогрессия. |
| 2. Рекуррентная. | 2. Формула. |
| 3. Геометрическая. | 3. Арифметическая. |
| 4. Последующий. | 4. Предыдущий. |
| 5. Разность. | 5. Знаменатель. |
| 6. Бесконечная. | 6. Сумма. |
| 7. Возрастающая. | 7. Убывающая. |
Чётные и нечётные функции
Вариант 1
1. Приведите пример чётной функции.
2. Дайте определение нечётной функции.
3. Область определения функции  . Может ли эта функция быть чётной или нечётной?
. Может ли эта функция быть чётной или нечётной?
4. Является ли чётной или нечётной функция:  ?
?
5. Известно, что  нечётная функция и
нечётная функция и  . Найдите
. Найдите  .
.
6. Известно, что чётная функция  на промежутке
на промежутке  принимает лишь отрицательные значения. Какие значения принимает функция на промежутке
принимает лишь отрицательные значения. Какие значения принимает функция на промежутке  ?
?
7. Сформулируйте свойства графика чётной функции.
8. График чётной или нечётной функции изображен на рисунке?
Вариант 2
1. Приведите пример нечётной функции.
2. Дайте определение чётной функции.
3. Область определения функции (–9; 9]. Может ли эта функция быть чётной или нечётной?
4. Является ли чётной или нечётной функция: ?
5. Известно, что  чётная функция и
чётная функция и  . Найдите
. Найдите  .
.
6. Известно, что нечётная функция  на промежутке
на промежутке  принимает лишь отрицательные значения. Какие значения принимает функция на промежутке
принимает лишь отрицательные значения. Какие значения принимает функция на промежутке  ?
?
7. Сформулируйте свойства графика нечётной функции.
8. График чётной или нечётной функции изображен на рисунке?
Ответы:
| Вариант 1 | Вариант 2 |
| 1. у = х2 | 1. у = х3 |
| 2. Функция  называется нечётной, если область её определения симметрична относительно нуля и для любого значения аргумента х верно равенство называется нечётной, если область её определения симметрична относительно нуля и для любого значения аргумента х верно равенство  | 2. Функция  называется нечётной, если область её определения симметрична относительно нуля и для любого значения аргумента х верно равенство называется нечётной, если область её определения симметрична относительно нуля и для любого значения аргумента х верно равенство  |
| 3. Нет | 3. Нет |
| 4. Чётная | 4. Нечётная |
| 5. | 5.  |
| 6. Отрицательные значения | 6. Положительные значения |
| 7. График любой чётной функции симметричен относительно оси ординат | 7. График любой нечётной функции симметричен относительно начала координат |
| 8. Нечётная | 8. Чётная |
Степенная функция
Вариант 1
1. Какой формулой задаётся степенная функция?
2. Какова область определения степенной функции, если показатель степени нечётный?
3. Какова область значений степенной функции, если показатель чётный?
4. Чему равно значение степенной функции, если аргумент равен нулю?
5. Какое значение принимает степенная функция с нечётным показателем, если аргумент положительный?
6. Когда степенная функция является чётной?
7. На каком промежутке возрастает степенная функция с чётным показателем?
8. Функция задана формулой  . Сравните
. Сравните  и
и  .
.
9. Функция задана формулой  . Сравните
. Сравните  и
и  .
.
10. Изобразите схематически график функции  .
.
Вариант 2
1. Запишите формулы степенных функций, которые изучались ранее, в 7 классе.
2. Какова область определения степенной функции, если показатель степени чётный?
3. Какова область значений степенной функции, если показатель нечётный?
4. Какое значение принимает степенная функция с чётным показателем, если аргумент отличен от нуля?
5. Какое значение принимает степенная функция с нечётным показателем, если аргумент отрицательный?
6. Когда степенная функция является нечётной?
7. На каком промежутке возрастает степенная функция с нечётным показателем?
8. Функция задана формулой  . Сравните
. Сравните  и
и  .
.
9. Функция задана формулой  . Сравните
. Сравните  и
и  .
.
10. Изобразите схематически график функции  .
.
Ответы:
| Вариант 1 | Вариант 2 |
| 1.  | 1.  , ,  , ,  |
| 2. Множество действительных чисел | 2. Множество действительных чисел |
| 3. Множество неотрицательных чисел | 3. Множество действительных чисел |
| 4. у = 0 | 4. у 0 |
| 5. Положительные значения | 5. Отрицательные значения |
| 6. При чётном показателе | 6. При нечётном показателе |
| 7. На промежутке [0; +) | 7. На всей области определения |
| 8.  | 8. = =  |
| 9.   | 9. |
| 10. | 10. |
| | |
Определение корня n-й степени
Вариант 1
1. Дайте определение корня п-й степени.
2. Как называется а в записи  ?
?
3. Запишите “корень пятой степени из х”.
4. При каком значении а имеет смысл выражение  , если n – чётное число?
, если n – чётное число?
5. Выразите  через арифметический корень той же степени.
через арифметический корень той же степени.
6. Имеет ли смысл выражение  ?
?
7. Вычислите  .
.
8. Найдите значение выражения:  .
.
9. Сколько корней имеет уравнение:  ?
?
Вариант 2
1. Дайте определение арифметического корня п-й степени.
2. Как называется n в записи  ?
?
3. Запишите “корень восьмой степени из у”.
4. При каком значении а имеет смысл выражение  , если n – нечётное число?
, если n – нечётное число?
5. Продолжите запись  .
.
6. Имеет ли смысл выражение  ?
?
7. Вычислите  .
.
8. Найдите значение выражения:  .
.
9. Сколько корней имеет уравнение:  ?
?
Ответы:
| Вариант 1 | Вариант 2 |
| 1. Корнем п-й степени из числа а называется такое число, п-я степень которого равна а | 1. Арифметическим корнем п-й степени из неотрицательного числа а называется неотрицательное число, п-я степень которого равна а |
| 2. Подкоренное выражение | 2. Показатель корня |
| 3.  | 3.  |
| 4.  | 4. При любом а |
| 5.  | 5. … = а |
| 6. Да | 6. Нет |
| 7. 2 | 7. 5 |
| 8. – 64 | 8. – 54 |
| 9. Один корень | 9. Ни одного корня |
Свойства корня N-й степени
Вариант 1
1. Закончите запись 
2. Закончите запись 
3. Найдите значение выражения:  .
.
4. Вычислите:  .
.
5. Вынесите множитель из-под знака корня:  .
.
6. Внесите множитель под знак корня:  .
.
7. Представьте выражение в виде дроби:  .
.
8. Упростите выражение:  .
.
9. Упростите выражение:  .
.
10. Запишите  в виде корня девятой степени.
в виде корня девятой степени.
Вариант 2
1. Закончите запись 
2. Закончите запись 
3. Найдите значение выражения:  .
.
4. Вычислите:  .
.
5. Вынесите множитель из-под знака корня:  .
.
6. Внесите множитель под знак корня:  .
.
7. Представьте выражение в виде дроби:  .
.
8. Упростите выражение:  .
.
9. Упростите выражение:  .
.
10. Запишите  в виде корня восьмой степени.
в виде корня восьмой степени.
Ответы:
| Вариант 1 | Вариант 2 |
| 1.  | 1.  |
| 2.  | 2.  |
| 3.  | 3. 10 |
| 4. 2 | 4.  |
| 5.  | 5.  |
| 6.  | 6.  |
| 7.  | 7.  |
| 8.  | 8.  |
| 9.  | 9.  |
| 10.  | 10.  |
Степень с дробным показателем
Вариант 1
1. Закончите запись  … .
… .
2. Представьте степень  в виде корня.
в виде корня.
3. Замените выражение  степенью с дробным показателем.
степенью с дробным показателем.
4. Укажите допустимые значения переменной в выражении:  .
.
5. Найдите значения выражения:  .
.
6. Представьте в виде степени:  .
.
7. Вычислите:  .
.
8. Упростите выражение:  .
.
9. Представьте в виде квадрата:  .
.
Вариант 2
1. Для какого основания определяется степень с любым дробным показателем.
2. Представьте степень  в виде корня.
в виде корня.
3. Замените выражение  степенью с дробным показателем.
степенью с дробным показателем.
4. Укажите допустимые значения переменной в выражении:  .
.
5. Найдите значения выражения:  .
.
6. Представьте в виде степени:  .
.
7. Вычислите:  .
.
8. Упростите выражение:  .
.
9. Представьте в виде куба:  .
.
Ответы
| Вариант 1 | Вариант 2 |
| 1.   | 1. Для положительного числа |
| 2.  | 2.  |
| 3.  | 3.  |
| 4.  | 4.  |
| 5. 3 | 5. 7 |
| 6.  | 6.  |
| 7.  | 7. 12 |
| 8.  | 8.  |
| 9.  | 9.  |