Математические диктанты по алгебре
(9 класс, учебник авт. А.Г.Мерзляк, В.Б.Полонский, М.С.Якир)
Диктант 1 по теме «Числовые неравенства»
1. Запишите окончание предложения:
1) считают, что число a больше числа b, если разность a − b является ... ;
2) считают, что число a меньше числа b, если разность a − b является ... ;
3) если a b или a = b, то верно неравенство ... ; 4) если a b или a = b, то верно неравенство ... .
2. Запишите в виде неравенства утверждение:
1) 8 больше 4;
2) −3 меньше −2;
3) 6 не больше 10;
4) 1 не меньше −5;
5) 2 не больше 2.
3. Сравните числа b и c, если:
1) b − c = 2; 2) c − b = −4.
4. Известно, что a b 0. Сравните с нулём значение выражения:
1) a2b; 2)  .
.
Диктант 2 по теме «Основные свойства числовых неравенств»
1. Запишите окончание предложения:
1) если a b и b c, то для чисел a и c верно неравенство ... ;
2) если a b и c — любое число, то для чисел a + c и b + c верно неравенство ... ;
3) если a b и c — положительное число, то для чисел ac и bc верно неравенство ... ;
4) если a b и c — отрицательное число, то для чисел ac и bc верно неравенство ... ;
5) если a b и ab 0, то для чисел  и
и  верно неравенство ... .
верно неравенство ... .
2. Известно, что a b. Запишите верное неравенство, которое получим, если:
1) к обеим частям неравенства прибавим число 6;
2) из обеих частей неравенства вычтем число 7;
3) обе части неравенства умножим на число −4;
4) обе части неравенства разделим на число 15.
3. Известно, что a 5. Сравните с нулём значение выражения:
1) a − 4; 2) −a; 3) (a − 1)(5 − a).
4. Сравните с нулём число x, если:
1) 6x x; 2) 0,6x 6x; 3) −5x x.
5. Сравните числа a и b, если известно, что:
1) a + 8 b; 2) a − 1 b.
6. Докажите, что если y −6, то 3y + 20 1.
Диктант 3 по теме «Сложение и умножение числовых неравенств. Оценивание значения выражения»
1. Запишите окончание предложения:
1) если a b и c d, то для чисел a + c и b + d верно неравенство ... ;
2) если a b, c d и a, b, c, d — положительные числа, то для чисел ac и bd верно неравенство ... ;
3) если a b и a, b — положительные числа, то для чисел an и bn, где n — натуральное число, верно неравенство ... .
2. Запишите неравенство, которое получим, если:
1) сложим почленно неравенства 8 −4 и 6 3;
2) перемножим почленно неравенства 5 2 и 7 6;
3) перемножим почленно неравенства 1,6 .
3. Известно, что 12 a
1) a + 5; 2) a − 3; 3) −a; 4)  .
.
4. Известно, что 3 x y
1) x + y; 2) xy; 3) x − y.
5. Оцените периметр P равностороннего треугольника со стороной a см, если 0,8 a S квадрата со стороной a см, если 3 a
7. Оцените площадь S прямоугольного треугольника с катетами a см и b см, если 4 a b
Диктант 4 по теме «Неравенства с одной переменной»
1. Запишите окончание предложения:
1) решением неравенства с одной переменной называют ... ;
2) решить неравенство означает ... ;
3) неравенства называют равносильными, если они ... .
2. Запишите какие-либо два решения неравенства 2x x − 3.
3. Запишите какие-либо два решения неравенства x2 − 9 ≤ 0.
4. Запишите какое-либо неравенство, множеством решений которого является:
1) множество действительных чисел;
2) пустое множество.
5. Запишите какое-либо неравенство, равносильное неравенству:
1) 
2) 
6. Решите неравенство:
1) 
2) 
Диктант 5 по теме «Решение линейных неравенств с одной переменной. Числовые промежутки»
1. Запишите правила, с помощью которых можно получить неравенство, равносильное данному.
2. Запишите окончание предложения:
1) линейными неравенствами с одной переменной называют неравенства вида ... ;
2) если решением неравенства является любое число, то промежуток, являющийся множеством решений этого неравенства, называют ... .
3. Изобразите на координатной прямой и запишите промежуток, который задаётся неравенством:
1) x x ≤ 7; 3) x 7; 4) x 7.
4. Запишите наименьшее целое число, принадлежащее промежутку:
1) (5; +∞); 2) [5; +∞); 3) (−8,5; +∞); 4) [−9,4; +∞).
5. Запишите наибольшее целое число, принадлежащее промежутку:
1) (−∞; −2); 2) (−∞; −6]; 3) (−∞; −3,1]; 4) (−∞; 2,7).
6. Решите неравенство:
1) 4x −12; 2) −5x −20; 3) 0x 3; 4) 0x
5) 0x x −4; 7) x + 2 −1; 8) 6 − x 4.
7. Запишите область определения функции:
1)  .
.
Диктант 6 по теме «Системы линейных неравенств с одной переменной»
1. Запишите окончание предложения:
1) решением системы неравенств с одной переменной называют ... ;
2) решить систему неравенств означает ... ;
3) чтобы решить систему неравенств, надо найти пересечение ... .
2. Запишите какие-либо два решения системы неравенств:
1) 
3. Изобразите на координатной прямой и запишите промежуток, который задаётся неравенством:
1) −2 x x x ≤ 0; 4) 1 x ≤ 2.
4. Запишите все целые числа, принадлежащие промежутку:
1) [2; 5]; 2) (7; 10]; 3) [−4,3; 0); 4) (−3; 1).
5. Запишите множество решений системы неравенств:
1) 
6. Запишите какую-либо систему линейных неравенств, множество решений которой:
1) состоит из одного числа;
2) является пустым множеством;
3) является числовой прямой.
Диктант 7 по теме «Повторение и расширение сведений о функции»
1. Запишите окончание предложения:
1) функция — это правило, с помощью которого по каждому значению независимой переменной из множества X можно найти ... ;
2) независимую переменную называют ... ;
3) областью определения функции называют ... ;
4) значение зависимой переменной называют ... ;
5) областью значений функции называют ... .
2. Функция задана формулой f (x) = −5x + 3. Найдите:
1) f (1); f (0);
2) значение аргумента, при котором значение функции равно 13.
3. Запишите область определения функции:
1) 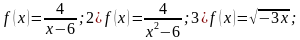
4) 
4. Запишите область значений функции:
1) 
5. Задайте аналитически какую-либо функцию, областью определения которой является: 1) множество действительных чисел;
2) множество действительных чисел, за исключением чисел −2 и 8;
3) промежуток  ;
;
4) промежуток (2; +∞).
Диктант 8 по теме «Свойства функции»
1. Запишите окончание предложения:
1) нулём функции называют ... ;
2) промежутком знакопостоянства функции называют промежуток, на котором ... ;
3) функцию f называют возрастающей на некотором промежутке, если для любых двух значений аргумента x1 и x2 из этого промежутка таких, что ... ;
4) функцию называют возрастающей на некотором промежутке, если для любых значений аргумента из этого промежутка меньшему значению аргумента ... ;
5) функцию f называют убывающей на некотором промежутке, если для любых двух значений аргумента x1 и x2 из этого промежутка таких, что ... ;
6) функцию называют убывающей на некотором промежутке, если для любых значений аргумента из этого промежутка меньшему значению аргумента ... .
2. Нарисуйте график какой-либо функции, нулями которой являются числа −4 и 2, принимающей положительные значения на промежутках (−∞; −4) и (2; +∞), а отрицательные значения — на промежутке (−4; 2).
3. Нарисуйте график какой-либо функции, нулями которой являются числа −3 и 3, принимающей отрицательные значения на промежутке (−∞; −3), а положительные значения — на промежутках (−3; 3) и (3; +∞).
4. Найдите нули функции:
1)  .
.
5. Задайте аналитически какую-либо функцию, определённую на множестве действительных чисел:
1) нулями которой являются числа −1 и 2;
2) имеющую три нуля.
6. Известно, что функция y = f (x) возрастающая. Сравните f (−2) и f (4).
7. Известно, что функция y = f (x) убывающая. Сравните f (3) и f (12).
8. Задайте аналитически какую-либо линейную функцию, являющуюся:
1) возрастающей; 2) убывающей.
9. Нарисуйте график какой-либо функции, определённой на множестве действительных чисел, которая:
1) возрастает на промежутке (−∞; 2] и убывает на промежутке [2; +∞);
2) убывает на промежутках (−∞; −1] и [1; +∞) и возрастает на промежутке [−1; 1].
Диктант 9 по теме «Построение графика функции y = kf (x)»
1. Запишите окончание предложения:
1) график функции y = kf (x), где k ≠ 0, можно получить, заменив каждую точку графика функции y = f (x) на точку ... ;
2) графиком функции y = ax2, где a ≠ 0, является ... ;
3) вершиной параболы y = ax2 является точка с координатами ... ;
4) при a 0 ветви параболы y = ax2 направлены ... ;
5) при a y = ax2 направлены ... ;
6) областью определения функции y = ax2, где a ≠ 0, является ... ;
7) областью значений функции y = ax2 при a 0 является промежуток ... ;
8) областью значений функции y = ax2 при a
9) при a 0 функция y = ax2 возрастает на промежутке ... ;
10) при a 0 функция y = ax2 убывает на промежутке ... ;
11) при a y = ax2 возрастает на промежутке ... ;
12) при a y = ax2 убывает на промежутке ... .
2. Изобразите схематически график функции y = ax2:
1) при a 0; 2) при a
3. Принадлежит ли графику функции y = −4x2 точка:
1) A (3; −36); 2) B  ?
?
4. При каком значении a график функции y = ax2 проходит через точку:
1) C (−1; 9); 2) D (5; −10)?
5. Укажите промежуток возрастания функции y = −6x2.
6. Укажите промежуток возрастания функции y = 14x2.
Диктант 10 по теме «Построение графиков функций y = f (x) + b и y = f (x + a)»
1. Запишите окончание предложения:
1) график функции y = f (x) + b можно получить в результате параллельного переноса графика функции y = f (x) на ... ;
2) график функции y = f (x + a) можно получить в результате параллельного переноса графика функции y = f (x) на ... ;
3) вершиной параболы y = x2 + b является точка с координатами ... ;
4) вершиной параболы y = (x + a)2 является точка с координатами ... ;
5) графиком функции y = k (x + a)2 + b, k ≠ 0, является парабола, равная параболе y = kx2, вершина которой находится в точке с координатами ... .
2. График какой функции получим, если график функции y = x2 параллельно перенесём:
1) на 5 единиц вверх;
2) на 2 единицы влево;
3) на 1 единицу вправо и на 6 единиц вниз?
3. График какой функции получим, если график функции  параллельно перенесём:
параллельно перенесём:
1) на 7 единиц вверх;
2) на 7 единиц вниз;
3) на 7 единиц вправо;
4) на 7 единиц влево?
4. График какой функции получим, если график функции 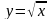 параллельно перенесём:
параллельно перенесём:
1) на 6 единиц влево и на 3 единицы вниз;
2) на 4 единицы вправо и на 5 единиц вверх?
5. Постройте график функции y = x2 − 3, укажите промежуток возрастания и промежуток убывания данной функции.
6. Постройте график функции y = 2 − x2, укажите промежуток возрастания и промежуток убывания данной функции.
7. Постройте график функции y = (x + 3)2, укажите промежуток возрастания и промежуток убывания данной функции.
Диктант 11 по теме «Квадратичная функция, её график и свойства»
1. Запишите определение квадратичной функции.
2. Запишите формулу, по которой можно найти абсциссу x0 вершины параболы
y = ax2 + bx + c.
3. Укажите направление ветвей параболы:
1) y = 7x2 + 7x + 1; 2) y = 9x − 2x2; 3) y = 4 − 2x − x2.
4. Найдите координаты вершины параболы:
1) y = 10x2 − 20x − 21; 2) y = −x2 + 4x + 1.
5. Найдите координаты точки пересечения с осью ординат параболы:
1) y =  x2 − 7x + 4; 2) y = −7x2 + x − 8.
x2 − 7x + 4; 2) y = −7x2 + x − 8.
6. Пусть D — дискриминант квадратного трёхчлена ax2 + bx + c. Изобразите схематически график квадратичной функции y = ax2 + bx +c, если:
1) a 0, D 0, c 0; 2) a 0, D a 0, D = 0;
4) a D 0, c a D a
7. Запишите промежуток возрастания функции y = x2 − 6x + 4.
8. Запишите промежуток убывания функции y = −x2 + 2x + 9.
Диктант 12 по теме «Процентные расчёты»
1. Сколько килограммов кислоты содержится в 20 кг шестипроцентного раствора?
2. Сколько километров составляет длина дороги из одного села в другое, если 24 км составляют 80 % длины этой дороги?
3. Каково процентное содержание соли в растворе, если в 600 г раствора содержится 30 г соли?
4. Цена товара возросла с 2400 р. до 3000 р. На сколько процентов повысилась цена?
5. Цена товара снизилась с 3000 р. до 2400 р. На сколько процентов снизилась цена?
6. Цену товара повысили на 40 %, а потом снизили на 40 %. Как изменилась первоначальная цена, повысилась или снизилась, и на сколько процентов?
7. Запишите формулу сложных процентов.
8. Вкладчик положил в банк 100 000 р. под 10 % годовых. Сколько денег будет на его счёте через 2 года?
9. Цена товара составляла 2000 р. Затем она была дважды снижена на 20 %. Какой стала цена товара?
10. После двух последовательных повышений цены на 50 % цена товара составила 225 000 р. Какой была первоначальная цена?
Диктант 13 по теме «Абсолютная и относительная погрешности»
1. Запишите окончание предложения:
1) абсолютной погрешностью приближения называют ... ;
2) относительной погрешностью называют отношение ... .
2. Известно, что x = 13,7 ± 0,2. Запишите этот факт в виде двойного неравенства.
3. Найдите абсолютную погрешность приближения числа 7,34 числом:
1) 7; 2) 7,3; 3) 7,4.
4. Найдите относительную погрешность приближения числа 2,7 числом 3.
Диктант 14 по теме «Основные правила комбинаторики»
1. Запишите окончание предложения:
1) если множество A состоит из m элементов, а множество B — из k элементов, причём эти множества не имеют общих элементов, то выбор «a или b», где a ∈ A, b ∈ B, можно осуществить ... ;
2) если элемент a можно выбрать m способами и после каждого такого выбора элемент b можно выбрать k способами, то выбор «a и b» в указанном порядке можно осуществить ...
2. Сколькими способами можно рассадить на четырёх стульях четырёх человек?
3. В компании по ремонту домов имеется 12 сантехников и 10 электриков. Сколькими способами можно составить бригаду из сантехника и электрика?
4. Сколько трёхзначных чисел можно записать с помощью цифр:
1) 7, 8, 9; 2) 0, 1, 2; 3) 5, 6, 7, 8?
5. Сколько трёхзначных чисел, все цифры которых должны быть различными, можно записать с помощью цифр:
1) 7, 8, 9; 2) 0, 1, 2; 3) 5, 6, 7, 8?
Диктант 15 по теме «Классическое определение вероятности»
1. Запишите окончание предложения:
1) событие, которое при данном комплексе условий обязательно состоится при любом испытании, называют ... ;
2) событие, которое при данном комплексе условий не может состояться ни при каком испытании, называют ... ;
3) вероятность достоверного события считают равной ... ;
4) вероятность невозможного события считают равной ... ;
5) для вероятности p любого события A выполняется неравенство ... ;
6) если испытание заканчивается одним из n равновозможных результатов, из которых m приводят к наступлению события A, то вероятностью события A называют ... .
2. В коробке лежат 10 белых и 15 красных шаров. Какова вероятность того, что выбранный наугад шар окажется:
1) белым; 2) синим; 3) белым или красным?
3. Из натуральных чисел от 1 до 10 наугад выбирают одно число. Какова вероятность того, что это число будет:
1) двузначным; 2) чётным; 3) кратным 5; 4) кратным 3;
5) делителем числа 36; 6) отрицательным; 7) простым;
8) кубом натурального числа?
Диктант 16 по теме «Числовые последовательности»
1. Запишите окончание предложения:
1) последовательности образуют объекты, которые ... ;
2) объекты, образующие последовательности, называют ... ;
3) последовательность называют числовой, если ... ;
4) существуют такие основные способы задания последовательности: ... .
2. Конечной или бесконечной является последовательность:
1) делителей числа 100 000; 2) кратных числа 6?
3. Запишите в порядке возрастания пять первых членов последовательности двузначных чисел, кратных числу 7.
4. Запишите первый член последовательности трёхзначных нечётных чисел.
5. Запишите последний член последовательности четырёхзначных чисел.
6. Запишите три первых члена последовательности (an), заданной формулой n-го члена
an = n2 + 3.
7. Запишите двадцатый член последовательности (bn), заданной формулой n-го члена
bn = 
8. Найдите второй и третий члены последовательности (cn), если c1 = 10, cn + 1 = 3cn.
Диктант 17 по теме «Арифметическая прогрессия»
1. Запишите окончание предложения:
1) арифметической прогрессией называют последовательность ... ;
2) любой член арифметической прогрессии, кроме первого, равен среднему арифметическому ... .
2. Запишите формулу n-го члена арифметической прогрессии.
3. Найдите второй член арифметической прогрессии, первый член которой равен −14, а разность равна 5.
4. Найдите разность арифметической прогрессии (an), если a7 = −4, a8 = 5.
5. Найдите девятый член арифметической прогрессии (an), если an = 2n − 3.
6. Найдите номер члена арифметической прогрессии (an), равного 9, если an = 5n − 21.
7. Чему равен тринадцатый член арифметической прогрессии (an), если a12 + a14 = 36?
8. Каждый член арифметической прогрессии с разностью d увеличили на 3. Будет ли полученная последовательность арифметической прогрессией? В случае утвердительного ответа укажите, чему будет равна разность прогрессии.
9. Каждый член арифметической прогрессии с разностью d разделили на 5. Будет ли полученная последовательность арифметической прогрессией? В случае утвердительного ответа укажите, чему будет равна разность прогрессии.
10. Каждый член арифметической прогрессии с разностью d, отличной от нуля, возвели в квадрат. Будет ли полученная последовательность арифметической прогрессией? В случае утвердительного ответа укажите, чему будет равна разность прогрессии.
Диктант 18 по теме «Сумма n первых членов арифметической прогрессии»
1. Запишите формулу, по которой можно найти сумму n первых членов арифметической прогрессии, если известны её первый и последний члены.
2. Запишите формулу, по которой можно найти сумму n первых членов арифметической прогрессии, если известны её первый член и разность.
3. Чему равна сумма шести первых членов арифметической прогрессии (an), если a1 = 12, a6 = 26?
4. Найдите сумму пяти первых членов арифметической прогрессии, первый член которой равен −3, а разность равна 5.
5. При любом n сумму n первых членов некоторой арифметической прогрессии можно вычислить по формуле Sn = n2 − 2n. Найдите два первых члена прогрессии.
6. Найдите сумму всех натуральных чисел, кратных 3, которые меньше 25.
7. Найдите сумму девятнадцати первых членов арифметической прогрессии (an), если
a10 = 20.
Диктант 19 по теме «Геометрическая прогрессия»
1. Запишите окончание предложения:
1) геометрической прогрессией называют последовательность ... ;
2) квадрат любого члена геометрической прогрессии, кроме первого, равен ... .
2. Запишите формулу n-го члена геометрической прогрессии.
3. Найдите второй член геометрической прогрессии, первый член которой равен 12, а знаменатель равен 0,3.
4. Найдите знаменатель геометрической прогрессии (bn), если b5 = 7, b6 = 35.
5. Первый член геометрической прогрессии равен 16, а второй член — 8. Найдите третий член прогрессии.
6. Найдите шестой член геометрической прогрессии, первый член которой равен 1, а знаменатель равен −2.
7. Чему равен десятый член геометрической прогрессии (bn), если b9 b11 = 16?
8. Каждый член геометрической прогрессии со знаменателем q, отличным от единицы, увеличили на 3. Будет ли полученная последовательность геометрической прогрессией? В случае утвердительного ответа укажите, чему равен знаменатель прогрессии.
9. Каждый член геометрической прогрессии со знаменателем q разделили на 5. Будет ли полученная последовательность геометрической прогрессией? В случае утвердительного ответа укажите, чему равен знаменатель прогрессии.
10. Каждый член геометрической прогрессии со знаменателем q возвели в квадрат. Будет ли полученная последовательность геометрической прогрессией? В случае утвердительного ответа укажите, чему равен знаменатель прогрессии.
Диктант 20 по теме «Сумма n первых членов геометрической прогрессии. Сумма бесконечной геометрической прогрессии, у которой модуль знаменателя меньше 1»
1. Запишите формулу, по которой можно найти сумму n первых членов геометрической прогрессии, знаменатель которой отличен от единицы.
2. Чему равна сумма n первых членов геометрической прогрессии, знаменатель которой равен единице?
3. Запишите формулу суммы бесконечной геометрической прогрессии, модуль знаменателя которой меньше единицы.
4. Найдите сумму пяти первых членов геометрической прогрессии, первый член которой равен 3, а знаменатель равен −2.
5. Вычислите сумму бесконечной геометрической прогрессии, первый член которой равен 12, а знаменатель равен 0,6.
6. Найдите первый член геометрической прогрессии, сумма которой равна 28, а знаменатель равен −0,4.
7. Представьте в виде обыкновенной дроби бесконечную десятичную периодическую дробь: 1) 0,888... ; 2) 4,(81).







 .
. и
и  верно неравенство ... .
верно неравенство ... .



 .
.

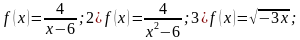


 ;
;  .
.  ?
?  параллельно перенесём:
параллельно перенесём: 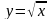 параллельно перенесём:
параллельно перенесём:  x2 − 7x + 4; 2) y = −7x2 + x − 8.
x2 − 7x + 4; 2) y = −7x2 + x − 8.




















