Математический кружок в V-VI классах.
Клепикова Наталья Владимировна
Учитель математики МБОУ СОШ №26
г. Ставрополя
г. Ставрополь
2019 г
План-оглавление
Введение………………………………………………………………………...………3
Цельи значение внеклассной работы мо математике………………...……………...4
Методика организации и проведения первых занятий математического кружка ….5
Математические игры и их роль в проведении кружковых занятий………………..11
Заключение……………………………………………………………………………...12
Список использованной литературы………………………………………….............13
Введение
Толковый словарь под редакцией С.И.Ожегова объясняет слово «одарённость» следующим образом: «То же, что талантливый…». Талантливый – «…это человек, обладающий врождёнными качествами, особыми природными способностями». Из этого определения следует, что неталантливых а, следовательно, не одаренных от природы людей не бывает. Когда нам предлагают «создать банк одаренных детей», то мы, недолго сомневаясь, вносим в список имена самых сильных учеников, самых старательных, ответственных, тех, кто не подведет на очередной олимпиаде или конференции. Вовсе не удивительно, что одаренными у нас оказываются одни и те же ребята и по математике, и по литературе, по иностранному языку и т. д. Но, мы знаем, что найти «одаренного», именно по своему предмету, очень сложно. Именно поэтому, основным направлением работы в школе является создание условий для оптимального развития одаренных детей, чья одаренность, может быть, еще не проявилась.
Учитель не должен ставить целью, выявление того, кто одарен больше, кто меньше, а дать возможность развиваться всем желающим детям. Творческое отношение к изученному предмету стимулирует проявление одаренности. Ведь, если ребенок радуется своему успеху, то эти положительные эмоции подталкивают его к развитию своих, пусть и очень небольших, способностей. Это очень важно для становления человеческой личности, на современном этапе. В процессе обучения дети должны научиться вырабатывать потребность развивать свои природные данные.
Развитие новых технологий повлекли за собой возросшую потребность общества в людях, которые обладают нестандартным мышлением. Не случайно, популярными стали слова известного психолога К.Роджерса (1987), что «если в современном обществе мы не будем иметь людей, которые конструктивно реагируют на малейшие изменения в общем развитии, мы можем погибнуть, и это будет та цена, которую мы все заплатим за отсутствие творческости». Школа, не может при формировании социального заказа не учитывать потребностей общества в развитии творческой личности. Раннее выявление, воспитание и обучение талантливых школьников является прекрасной возможностью для выполнения этой задачи. Естественным продолжением и дополнением основных форм организации учебно-познавательой деятельности учащихся на уроке, является внеклассная работа.Наряду с учебно–познавательной деятельностью учащихся на уроке деятельностью, важной является внеклассная работа.
Наиболее важными задачами внеклассной работы на современном этапе развития школы являются следующие:
пробуждение и развитие устойчивого интереса учащихся к математике и ее приложениям;
расширение и углубление знаний учащихся по программному материалу;
развитие математических способностей и мышления у учащихся;
развитие у учащихся умения самостоятельно и творчески работать с учебной и научно-популярной литературой;
создание актива, способного оказать учителю математики помощь в организации эффективного обучения математике всего коллектива данного класса;
расширение и углубление представлений учащихся о практическом значении математики в технике, экономике;
расширение и углубление представлений учащихся о культурно-исторической ценности математики, о роли ведущих ученых-математиков в развитии мировой науки;
осуществление индивидуализации и дифференциации;
разностороннее развитие личности.
Цель и значение внеклассной работы по математике.
Обучая математике недостаточно ограничиваться рамками обучения только на уроках, необходимо будить в учениках творческую активную мысль и интерес к посильной исследовательской работе. Большое поле творческой деятельности дает внеклассная работа.
Внеклассная работа, являясь неотъемлемой частью всей учебно-воспитательной работы в школе, имеет свои особенности. Эти занятия организуются на строго добровольных началах, проводятся в разнообразных формах и позволяют учащемуся проявлять свой интерес к определенным видам занятий, предусмотренным планом внеклассной работы.
На внеклассных занятиях легче привлечь учащихся к самостоятельной творческой деятельности, к самостоятельной работе над учебником, к подбору материала из различных источников.
Обычно, на занятиях математического кружка рассматриваются вопросы, имеющие какой-нибудь особый интерес. Это или исторические вопросы, или вопросы теоретические, не входящие в программу, или углубление отдельных понятий, рассмотренных в классе.
На кружковых занятиях, учащиеся узнают от своего руководителя или из сообщений своих товарищей много нового и интересного, и их кругозор расширяется.
Внеклассная работа будет хорошо поставлена тогда, когда она обеспечит каждого ученика практическим заданием соответственно его силам и способностям.
Одной из важных задач внеклассной работы является привитие учащимся практических навыков и умений. В классе учитель не всегда может успеть рассмотреть достаточное количество примеров и задач, которые обеспечили бы сознательное применение учениками теории.
Некоторые мероприятия кружка, например подготовка к математическим олимпиадам, способствует укреплению и развитию у учащихся математических навыков.
Таким образом, одной из наиболее эффективных форм развития математических дарований является систематическая внеклассная работа.
Основными принципами кружковой работы являются: учет возрастных особенностей, демократичность, т.е. заниматься приходят все желающие, интересность, доступность, расширение учебного материала. В 5-6 классах продолжается формирование компонентов математических способностей. Кроме того задания в этой возрастной группе должны развивать гибкость мышления, стремление к более рациональному решению задачи. В программу кружков 5 и 6-х классов включаются такие темы, как «Принцип Дирихле», «Круги Эйлера», «Графы», «Ряды натуральных чисел», а по темам «Признаки делимости», «Проценты», «НОК и НОД» идет расширение урочного материала. Также рассматриваются задачи на части, на движение, на дроби, на составление уравнений и логические. В содержание внеклассной работы включаются вопросы, выходящие за рамки школьной программы по математике, но примыкающие к ней. Это признаки делимости чисел на 7; 11, исторические экскурсы по той или иной теме, математические софизмы, задачи повышенной трудности и т.д. В содержание внеклассной работы необходимо включать и вопросы, вошедшие в содержание математического образования в последние десятилетия: логика, теория вероятностей, комбинаторика и т.п.
На последних занятиях кружка в конце года, проведение математической выставки вызывает особый интерес и желание участвовать в ней.На выставке желательно экспонировать творческие работы самих ребят. Здесь уже идет речь о другой форме проведения внеклассной работы по математике, сочинение детьми математических сказок и написание сочинений на математическую тему. Перед началом такой работы учителю целесообразней дать детям некоторый образец и преподнести его в увлекательной, интересной форме. Сказку можно инсценировать или нарисовать и показать на слайдах.
В отличие от урока на кружковых занятиях знания не даются, не передаются, а выстраиваются поэтому, возможно, что так до конца занятия и не прозвучит истина, которую знает учитель. Тем самым создается хорошая посылка для размышлений. В кружке у учащихся развивается мотивация, интерес к предмету, креативное мышление и воображение. Дети, делая пусть небольшие открытия, лучше их запоминают и лучше могут их использовать в разных ситуациях. У ребят развиваются умения и желания сотрудничать при выполнении коллективной творческой деятельности. Идет становление позитивной, адекватной Я-концепции.
Проведение занятий в математическом кружке, организация различных форм работы, требуют особой подготовки, тем самым побуждают учителя прибегать к разнообразным источникам, что повышает его квалификацию
Методика организации и проведения занятий математического кружка
Первые занятия математического кружка имеют свою специфику, обусловленную особыми задачами, стоящими в начале организационного периода.
Привлечение любителей математики к кружковой работе и возбуждение интереса к математическим занятиям.
Выявление индивидуальных склонностей и способностей учащихся, вступивших в кружок.
Сплоченность коллектива кружковцев.
Кружок работает по плану, который рассматривается на методическом объединении. Занятия можно планировать 3 раза в месяц по 1-1,5 часа. Начинать работу кружка лучше с середины сентября или с 1 октября, а завершить в конце апреля (начале мая). В течение года кружковые занятия должны увязываться с другими формами внеклассной работы по математике, в подготовке и проведении которых активное участие должны принимать члены кружка. В каникулы предметные кружки проводить не рекомендуется.
Каждому ученику дается конкретное задание, которое он обязан выполнить. Доклады поручать надо более подготовленным кружковцам, чтобы избежать ослабления внимания у учащихся. Темы выбираются доступные и интересные. Доклады должны чередоваться с другими формами работы: интересными сообщениями учителя, разбором ошибок в математических рассуждениях, решением занимательных задач, составлением математических кроссвордов, практическими работами. О работе кружка должны знать многие учащиеся, поэтому необходимо проводить открытые занятия кружка.
В основу составления плана работы математического кружка должны быть положены следующие оправдывающие себя принципы:
углубление изученного материала;
привитие учащимся практических навыков;
сообщение сведений из истории развития математики;
решение примеров и задач повышенной трудности;
использование занимательной математики.
Доступность излагаемого материала.
На первых занятиях кружка рассматриваются вопросы, для понимания которых не требуется большой математической подготовки. Например: «Палочки Непера», «Занятия с циркулем», «Составление и распространение узоров на клетчатой бумаге», «Заполнение плоскости равными фигурами», «Упражнения с куском бумаги», «Развлечения с разрезным квадратом и др.» Соответственно должны быть составлены упражнения по принципу «минимум знаний - максимум смекалки», способствующие выявлению индивидуальных склонностей и способностей учащихся.
Перспективность тематики.
Тематика первых занятий кружка не должна быть случайной. Разрабатывая её, учитель должен явно представлять себе дальнейшие перспективы изучения того или иного вопроса. Например, развлечения с разрезным квадратом служат введением в важную тему «Равновеликость и равносоставленность фигур»; знакомство с устройством и применением палочек Непера- это лишь первый этап в изучении счетно-вычислительной техники. И таких тем можно подобрать сколько угодно.
Жизненность тематики.
Раскрываемые на первых занятиях кружка темы должны быть тесно связаны с программой и иметь практическое значение для учащихся. Слишком отвлеченные и далекие от программы задания могут оттолкнуть от кружковой работы отдельных учащихся, не имеющих большой тяги к абстрактным математическим рассуждениям, но, возможно, обладающих большой склонностью к прикладным сторонам математики (например, к вычислительной технике), на базе которых можно прививать более глубокий интерес и к теоретическим проблемам математики. Перечисленные ранее темы связаны с определенным разделом программы. Изучение их в кружке способствуют приобретению умений и навыков, необходимых в практической работе школьника («Палочки Непера»- вычислительные навыки; развлечения с разрезным квадратом - геометрический глазомер).
В основе методики организации и проведения внеклассных занятий по математике лежат интерес и активность. В организационный период особенно важно заинтересовать детей кружковой работой и активизировать деятельность при выполнении поручаемых работ. Отсюда особое значение в организационный период приобретают такие моменты в характере кружковой работы, как соединение интеллектуальной деятельности с физическим трудом, самостоятельное творчество учащихся, коллективный труд, которые способствуют повышению их интереса и активности.
Завершенность в работе.
Важно, чтобы всякая начатая на занятиях кружка работа была доведена до логического завершения, причем результаты работы должны быть оформлены таким образом, чтобы, созерцая их, учащиеся почувствовали не, только удовлетворение от сознания выполненной работы, но и эстетическое удовольствие. Например, составление задачника исторических задач, собранных кружковцами, будет практическим завершением этой работы.
«Завершенности» следует добиваться как в больших, так и в малых делах кружковцев. Даже новый прием устного счета, объясненный на занятиях математического кружка, можно «завершить» весьма эффективно, если, например, организовать игру, где бы основой служили вычисления по новой формуле.
Примерная программа кружка учащихся V класса
| № п/п | Тема занятия | Кол-во часов |
| 1. | Замечательные числа. Число 9. Метод проверки арифметических действий с помощью девятки. | 2 |
| 2. | Арифметические ребусы | 2 |
| 3. | Простые числа. «Решето» Эратосфена. | 1 |
| 4. | Цифры различных народов | 1 |
| 5. | Математические игры и фокусы «Волшебная» таблица. «Волшебные» часы. Кто первый скажет сто. Отгадать задуманное число. | 3 |
| 6. | Занимательные задачи на спичках | 2 |
| 7. | Арифметика каменного века. | 1 |
| 8. | Как ценили математику наши предки | 1 |
| 9. | Открытие нуля. | 1 |
| 10. | Великолепная семерка. | 1 |
| 11. | Палочки Непера (умножение чисел) | 2 |
| 12. | Задачи на комбинации и расположения | 2 |
| 13. | Красивые многогранники и их изготовление | 3 |
| 14. | Магницкий Леонтий Филиппович – автор первого учебника по математике в России | 1 |
| 15. | Метрическая система мер в России. Решение задач. | 2 |
| 16. | Решение задач на взвешивание | 2 |
| 17. | Решение олимпиадных задач | 2 |
| 18. | Итоговое занятие. Выставка работ. | 1 |
| Всего 30 часов |
Одной из важнейших задач школы является воспитание культурного человека. В связи с этим каждый предмет должен взять дополнительные, не свойственные ему функции. Геометрия – это феномен общечеловеческой культуры. Она располагает огромными возможностями для эмоционального, эстетического и духовного развития школьника. На занятиях математического кружка «Наглядная геометрия» можно показать всю многогранность геометрии.
В 5-6 классах математическое развитие происходит в рамках своеобразной триады: число – фигура – слово. Реализовать это можно занимаясь геометрией.
План работы кружка в 6 классе по учебному пособию «Наглядная геометрия» (35 ч.)
| № п/п | Тема занятия | Кол-во часов |
| 1 | Фигурки из кубиков и их частейФигурки из кубиков и их частей | 2 |
| 2 | Параллельность и перпендикулярность | 2 |
| 3 | Параллелограммы | 2 |
| 4 | Координаты | 2 |
| 5 | Оригами | 2 |
| 6 | Замечательные кривые | 2 |
| 7 | Кривые дракона | 2 |
| 8 | Лабиринты | 2 |
| 9 | Геометрия клетчатой бумаги | 2 |
| 10 | Зеркальное отражение | 2 |
| 11 | Симметрия | 2 |
| 12 | Симметрия помогает решать задачи | 2 |
| 13 | Бордюры | 2 |
| 14 | Орнаменты | 2 |
| 15 | Фигура окружность и ее свойства | 2 |
| 16 | Задачи головоломки | 3 |
Приведем примерные методические разработки занятий кружка на следующие темы: «Палочки Непера», «Развлечение с разрезным квадратом», «Моделирование звездчатых многогранников (по Венниджеру)»
Занятие на тему: «Палочки Непера»,
Принадлежности: листок плотной бумаги или картона (15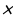 15см), масштабная линейка, ножницы
15см), масштабная линейка, ножницы
Организация работы. Вначале учитель объясняет принцип устройства палочек Непера и работы с нами. Для этого используются демонстрационные палочки размером 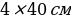 , изготовленные заранее кем-нибудь из кружковцев по заданию руководителя кружка. Для демонстрации необходимо иметь 3-4 такие «палочки». Затем учащиеся мастерят их сами. На рисунке показано, как можно сделать один комплект палочек.
, изготовленные заранее кем-нибудь из кружковцев по заданию руководителя кружка. Для демонстрации необходимо иметь 3-4 такие «палочки». Затем учащиеся мастерят их сами. На рисунке показано, как можно сделать один комплект палочек.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0         0 | 0 1 | 0 2 | 0 3 | 0 4 | 0 5 | 0 6 | 0 7 | 0 8 | 0 9 |
| 0 0 | 0 2 | 0 4 | 0 6 | 0 8 | 1 0 | 1 2 | 1 4 | 1 6 | 1 8 |
| 0 0 | 0 3 | 0 6 | 0 9 | 1 2 | 1 5 | 1 8 | 2 1 | 2 4 | 2 7 |
| 0 0 | 0 4 | 0 8 | 1 2 | 1 6 | 2  0 0 | 2 4 | 2 8 | 3 2 | 3 6 |
| 0 0 | 0 5 | 1 0 | 1 5 | 2 0 | 2 5 | 3  0 0 | 3 5 | 4 0 | 4 5 |
| 0 0 | 0 6 | 1 2 | 1 8 | 2 4 | 3 0 | 3 6 | 4 2 | 4 8 | 5 4 |
| 0 0 | 0 7 | 1 4 | 2 1 | 2 8 | 3 5 | 4 2 | 4 9 | 5  6 6 | 6 3 |
| 0 0 | 0 8 | 1 6 | 2 4 | 3 2 | 4 0 | 4 8 | 5 6 | 6 4 | 7 2 |
| 0 0 | 0 9 | 1 8 | 2 7 | 3 8 | 4 5 | 5 4 | 6 3 | 7 2 | 8 1 |
После этого начинаются практические вычисления с помощью палочек Непера. В программу занятий можно включить умножение многозначных чисел на однозначные и многозначные, деление чисел. В заключении провести игру «Кто скорее». К доске приглашаются лучшие счетчики из желающих. Они умножают многозначные числа на доске обычным способом, а все остальные - на палочках Непера. Кто скорее?
Уместно при этом рассказать учащимся о вычислительных машинах, привести следующие, весьма поучительные сравнения. Опытный вычислитель, работающий на настольном клавишном арифмометре, способен сделать 200-300 тыс. операций в год. Далее предложить кружковцам к следующему занятию подготовить сообщение о развитии ЭВМ в нашей стране.
В процессе работы с палочками Непера развиваются вычислительные способности. Новый непривычный способ вычисления требует большой сосредоточенности и быстрой ориентации в новых условиях. Знакомство с устройством палочек Непера и самостоятельное изготовление прибора способствует повышению интереса вообще к счетным приборам. Имеются широкие возможности для приложения творческих способностей при самостоятельном конструировании прибора на основе палочек Непера.
Занятия с разрезным квадратом
Широко известна старинная китайская головоломка «танграм»-составление фигурок из семи частей квадрата. Хотя эта игра носит развлекательный характер, в ней много поучительного: 1) складывая фигурки из частей квадрата, дети практически осваивают свойства равновеликости и равносоставленности фигур; 2) в процессе поисков решения развиваются комбинаторные навыки, геометрический глазомер, сообразительность, смекалка.
Принадлежности: кусочек картона 1-2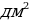 для изготовления разрезного квадрата, масштабная линейка, циркуль и карандаш.
для изготовления разрезного квадрата, масштабная линейка, циркуль и карандаш.
Организация работы Учащимся предлагается «построить» квадрат из листка гладкой бумаги с неопределенными краями. Это интересное занятие как бы вводит в практическую работу и имеет целью напомнить о свойствах квадрата, которые учащиеся невольно должны использовать в процессе его «построения». Из бумажного квадрата вырезают квадрат нужных размеров ( ), который используется как шаблон. Затем по шаблону изготовляют разрезной квадрат из картона, составляют фигурки из частей квадрата («свеча», «наездник» и др.). Кто скорее сложит? Для образца вывешиваются силуэты фигурок без обозначения контуров составляющих частей.
), который используется как шаблон. Затем по шаблону изготовляют разрезной квадрат из картона, составляют фигурки из частей квадрата («свеча», «наездник» и др.). Кто скорее сложит? Для образца вывешиваются силуэты фигурок без обозначения контуров составляющих частей.




Занятия с разрезным квадратом проходят живо и интересно. Этим занятиям можно придать исследовательский характер: поиски новых фигурок, какие можно составить из частей квадрата, являются первым, наиболее простым и доступным видом исследовательской работы учащихся. В процессе такой работы, носящий созидательный характер, проявляются фантазии детей, их интересы, способности. В ходе составления фигурок следует их фотографировать и затем помещать в школьную газету с указанием фамилии автора.
В заключении предлагается снова сложить квадрат из частей, (что не просто сделать). Предложить учащимся в качестве домашнего задания изготовить по нескольку таких квадратов для показа своим одноклассникам, друзьям, родителям.
Глубокое развитие и научное обоснование получил вопрос о взаимосвязи и взаимозависимости между физическим (ручным) трудом школьников и их умственным развитием в работах известного педагога В.А. Сухомлинского (1918-1970). «Ручной труд с использованием простых инструментов, - считал он, - является важным условием развития не только трудового мастерства, но и разума, наклонностей, способностей детей». При этом решающее значение он придавал не физическим усилиям, а именно, расчету, мастерству.
Особенно высок интерес у подростков к коллективному труду: «для подростка значение жизни и деятельности в коллективе… очень велико» (В.А. Крутецкой). Занятия кружка по моделированию звездчатых многогранников (по Венниджеру) является не только коллективным, но интересным и творческим.
Занятие кружка по моделированию звездчатых многогранников (по Венниджеру)
Тема занятий: Коллективное изготовление модели шестой звездчатой формы икосаэдра
На кружковых занятиях такого рода следует специально создавать ситуации, вызывающие «производственные трудности», для преодоления которых требуется не только математическая, но и техническая смекалка. Дети ставятся в условия, при которых им необходимо используя циркуль и линейку изготовить звездчатый многогранник. Выбор этого многогранника в качестве объекта для первого занятия кружка не случаен: это простая и прочная модель; дефекты, которые неизбежно допускаются учащимися на первом занятии при вырезании и склеивании заготовок, скрадываются благодаря своим конструктивным особенностям.
Принадлежности: несколько одинаковых стандартных листов нелинованной бумаги, лист плотной белой бумаги (ватман), ножницы, линейка, карандаш, клей, кусок картона для подстилки при резании и склеивании.
Организация работы. Учитель показывает слайды с изображениями моделей звездчатых многогранников (из книги М. Венниджера), рассказывает о процессе образования звездчатых форм из правильных многогранников.
В процессе работы выявляются конструктивные особенности звездчатых многогранников (в частности шестой звездчатой формы икосаэдра), ограниченных с внешней стороны различного вида многоугольниками. Поясняется, что модели звездчатых многогранников будут монтироваться из отдельных деталей заготовок. Эти детали (заготовки) вырезают из трафарета – специального чертежа, содержащего образцы деталей всех звездчатых форм, получаемых на базе правильного многогранника данного вида.
Задание.
Изготовить модель многогранника звездчатой формы, (необычная постановка задачи для пятиклассника имеет целью удивить, заинтересовать, активизировать учащихся на первом этапе её решения, дать полную свободу в осмыслении ситуации и оценке своих возможностей).
Как это сделать?
Вырезать из трафарета детали шестой звездчатой формы икосаэдра и изготовить их по образцу (путем обводки) из плотной бумаги по пять экземпляров каждой детали так, чтобы можно было их склеивать в блоки – «кольцо», «пики».

Соединить в «кольцо» пять малых деталей и в «пик» - пять деталей другого вида. Продев пик сквозь отверстие в кольце, закрепить его, приклеив к кольцу, При этом образуется основной фрагмент модели многогранника. Из 12 таких фрагментов составляется шестая форма звездчатого икосаэдра
Сборку модели (склеивание фрагментов) следует поручить двум трем учащимся.
Итогом этой работы может служить выставка работ кружковцев.В день открытия выставки проходит ее «презентация», то есть учитель рассказывает детям о представленных на выставке работах.
Принимая участие в коллективном труде, ученик чувствует большую ответственность, так как постоянно испытывает контроль; ему приходиться все время помнить, что от качества его работы зависит общий результат. Учащиеся 5-6 классов охотно принимают участие в таких занятиях.
Коллективный труд мобилизует учащихся, пробуждает их творческие силы, развивает индивидуальные способности.
Коллективные формы труда можно использовать при изготовлении некоторых геометрических фигур, например, звездчатых и полуправильных многогранников. Конструктивные особенности этих фигур таковы, что применение коллективных форм труда вызывается педагогическими соображениями: нецелесообразно, например, при монтировании звездчатого додекаэдра все двенадцать пирамидок («игл») поручать клеить одному ученику-труд утомительный и в педагогическом отношении бесцельный. Но если эту работу выполняет коллектив, то каждому учащемуся достается изготовить определенную часть фигуры.
Математические игры и их роль в проведении кружковых занятий
Большую роль на кружковых занятиях по математике в 5-6 классах играют игры, главным образом дидактические. Основная их ценность в том, что они возбуждают интерес детей, усиливают эффект самого обучения. Создание игровых ситуаций приводит к тому, что дети увлечены игрой и незаметно для себя и без особого труда и напряжения приобретают определенные знания, умения и навыки. Игра делает отдельные элементы внеклассной работы по математике эмоционально насыщенными, вносит бодрый настрой в детский коллектив, помогает эстетически воспринимать ситуацию, связанную с математикой: праздничное оформление класса, красочные оригинальные газеты, красоту древней легенды, включающей задачу, драматизацию математического задания, наконец, стройность мыслей при решении логических задач. Игра так же содействует воспитанию дисциплинированности, так как проводится по правилам.
Правила должны быть простыми, точно сформулированными, доступными.Игра не должна вызывать слишком бурной реакции детей.Дидактический материал должен быть прост в изготовлении и удобен в использовании.Если игра предполагает соревнование команд, то должен быть контроль и открытый учет результатов.Дети должны активно участвовать в игре, а не бездействовать в длительном ожидании.Легкие игры должны чередоваться с более трудными. В конце должна быть проведена наиболее легкая и живая игра.Если на нескольких занятиях проводятся игры, связанные со сходными мыслительными действиями, то по содержанию математического материала должен соблюдаться принципот простого к сложному, от конкретного к абстрактному. Подвижные игры должны чередоваться со спокойными.
Игровой характер проведения внеклассных занятий по математике должен иметь определенную меру. Игры имеют познавательное значение, поэтому на первом плане должны оказаться умственные задания, для решения которых в мыслительной деятельности должны использоваться сравнение, анализ и синтез, суждения и умозаключения. Надо предоставлять детям возможность высказаться.В процессе игры должно быть выполнено определенное законченное действие, решено конкретное задание, а после игры сделан вывод.При подборе игр учителю необходимо продумывать следующие моменты:- цель игры;- количество участвующих;- необходимые материалы и пособия;- как ознакомить детей с правилами игры в минимальные сроки;- длительность игры (игра не должна быть “затянутой”, чтобы дети захотели вернутся к ней);- как обеспечить наиболее полное участие детей в игре;- как организовать наблюдение за детьми в процессе игры, чтобы понять, интересна ли она им;- как можно использовать основу игры с другим математическим материалом;- какие выводы должны сделать дети после игры.
Кроме того, математические игры могут быть настольными и подвижными. В первом случае материал для нее могут изготовить сами дети на уроках труда или рисования (например, математическое лото). Примером подвижной игры может служить математическая эстафета. Игры могут быть и такими, в которые дети могут играть и без помощи учителя.
Тематическое планирование курса (17,5 часов)
| № п/п | тема | кол-во часов |
| 1 | Фигурки из кубиков и их частей | 1 |
| 2 | Параллельность и перпендикулярность | 1 |
| 3 | Параллелограммы | 1 |
| 4 | Координаты | 1 |
| 5 | Оригами | 1 |
| 6 | Замечательные кривые | 1 |
| 7 | Кривые дракона | 1 |
| 8 | Лабиринты | 1 |
| 9 | Геометрия клетчатой бумаги | 1,5 |
| 10 | Зеркальное отражение | 1 |
| 11 | Симметрия | 1 |
| 12 | Бордюры | 1 |
| 13 | Орнаменты | 1 |
| 14 | Симметрия помогает решать задачи | 1 |
| 15 | Фигура окружность и её свойства | 1 |
| 16 | Задачи головоломки | 1 |
| 17 | Задачи головоломки | 1 |
Тематическое планирование курса (17,5 часов)
| № п/п | тема | кол-во часов |
| 1 | Фигурки из кубиков и их частей | 1 |
| 2 | Параллельность и перпендикулярность | 1 |
| 3 | Параллелограммы | 1 |
| 4 | Координаты | 1 |
| 5 | Оригами | 1 |
| 6 | Замечательные кривые | 1 |
| 7 | Кривые дракона | 1 |
| 8 | Лабиринты | 1 |
| 9 | Геометрия клетчатой бумаги | 1,5 |
| 10 | Зеркальное отражение | 1 |
| 11 | Симметрия | 1 |
| 12 | Бордюры | 1 |
| 13 | Орнаменты | 1 |
| 14 | Симметрия помогает решать задачи | 1 |
| 15 | Фигура окружность и её свойства | 1 |
| 16 | Задачи головоломки | 1 |
| 17 | Задачи головоломки | 1 |
Тематическое планирование курса (17,5 часов)
| № п/п | тема | кол-во часов |
| 1 | Фигурки из кубиков и их частей | 1 |
| 2 | Параллельность и перпендикулярность | 1 |
| 3 | Параллелограммы | 1 |
| 4 | Координаты | 1 |
| 5 | Оригами | 1 |
| 6 | Замечательные кривые | 1 |
| 7 | Кривые дракона | 1 |
| 8 | Лабиринты | 1 |
| 9 | Геометрия клетчатой бумаги | 1,5 |
| 10 | Зеркальное отражение | 1 |
| 11 | Симметрия | 1 |
| 12 | Бордюры | 1 |
| 13 | Орнаменты | 1 |
| 14 | Симметрия помогает решать задачи | 1 |
| 15 | Фигура окружность и её свойства | 1 |
| 16 | Задачи головоломки | 1 |
| 17 | Задачи головоломки | 1 |
Заключение
Математический кружок – это самодеятельное объединение учащихся под руководством педагога, в рамках которого проводятся систематические занятия с учащимися во внеурочное время.
Проведение кружковых занятий в значительной степени близко к урокам. Сходство классных и внеклассных занятий определяется организационной формой коллективной учебной работы, когда учитель ведет занятие с группой учащихся, проводит необходимые пояснения, спрашивает учащихся и тому подобное. При этом желательно учащимся предоставлять больше инициативы, давать им больше возможностей высказывать собственные суждения по обсуждаемому вопросу. Надо учесть, что иногда ошибочные рассуждения и их опровержения, тренировка в “разговоре” на математические темы дает учащимся больше пользы, чем изложение учителем готовых решений. Ребята нуждаются в развитии собственной инициативы, своего личного подхода к решению данной задачи. Важно поощрять различные способы решения задач, не стремиться навязывать свое решение. Вместе с тем, учителю необходимо следить за тем, чтобы тематика занятий и методы работы в кружке были разнообразной. Ценность содержания внеклассной работы и определяется разнообразием тематики и методов решения задач, новизной по отношению к содержанию урока математики в классе. Но основной отличительной особенностью кружковой работы является принцип добровольности вовлечения в работу.
На кружковых занятиях школьников обязательно надо учить ориентироваться в незнакомых ситуациях и областях, решать задачи на незнакомую фабулу, с непривычным для них математическим содержанием. Темп проведения кружковых занятий должен постепенно возрастать. Нецелесообразно на занятиях кружка проводить систематическое повторение ранее пройденных вопросов, так как основная задача кружковой работы - развитие творческого подхода, повышение уровня математической подготовки, но не сообщение учащимся определенных математических фактов, подлежащих обязательному усвоению. Учитель на занятиях не должен стеснять инициативы и находчивости учащихся в поисках решения задачи, облегчения вычислений. Кроме того, для занятий необходимо подбирать такие задания, которые представляют собой развитие типовых задач, предусмотренных или непредусмотренных программой
Математические кружки являются основной формой внеклассной работы по математике с учащимися в 5-6 классах. Для тех школьников, которые пока не проявляет заметной склонности к математике, эти занятия могут стать толчком в развитии их интереса к предмету и вызвать желание узнать больше. Кроме того, хотя эти вопросы и выходят за рамки обязательного содержания, они, безусловно, будут способствовать совершенствованию и развитию важнейших математических умений, предусмотренных программой. Руководство внеклассной работой по математике – большая работа учителя. Она требует от него любви к этому делу, большого желания дать детям возможность получить всестороннее развитие. Учитель не должен уставать удивляться красоте и мощи математических методов и должен постоянно восхищать этим своих учеников. Это трудно, на это нужно много душевных и физических сил, причем изо дня в день, но в этом суть профессии – учитель, а значит это нужно делать.
«Учитель математики должен быть очень терпеливым, потому что нельзя ожидать от учеников мгновенных результатов. Если делается все (в смысле разумной достаточности), делается профессионально и честно, то рано или поздно ученик себя проявит. Нужно терпеливо ждать".
Список литературы
Лейтес Н.С. Психология одаренных детей и подростков. – М.: Академия, 1996
Лейтес Н.С. Умственные способности и возраст.- М.: Педагогика, 1971
Давыдов В.В. Проблемы развивающего обучения. М.: Педагогика, 1986
Фарков А.В. Внеклассная работа по математике. М.: Айрис-пресс, 2006г
Генкин С.А., Итенберг И.В., Фомин Д.В. Ленинградские математические кружки. Киров.: АСА, 1994
Балк М.Б., Балк Г.Д. Математика после уроков М.: Просвещение, 1971
Festival. 1 september. ru. / subjects ( 1 )
Спивак А. В. Математический праздник. М.: Бюро Квантум, 2000.
Спивак А. В. Математический кружок. М.: Просвещение, 2003
Фарков А. В. Математические кружки в школе. 5 – 8 классы. М.: Айрис-пресс, 2006.
Festival. 1 september. ru. / subjects ( 1 ) СпивакА. В. Математическийкружок. М.:
Ф.Ф.Нагибин, Е.С. Капин. Математическая шкатулка, Москва, «Просвещение», 1984
Шейнина О.С., Соловьева Г.М. Математика. Занятия школьного кружка. 5-6 кл. М.:Издательство НЦ ЭНАС, 2003. С.208.
Просвещение, 2003 Тихомирова Л.Ф. Развитие интеллектуальных способностей школьника. Популярное пособие для родителей и педагогов. - Ярославль: Академия развития, 1996.
Барвин И.И., Фрибус Е. А. Старинные задачи: Кн. Для учащихся.- М.: Просвещение, 1994.
Шарыгин И.Ф., Ерганжиева Л.Н. Наглядная геометрия: Учебное пособие для учащихся V – VIклассов. – МИРОС, 1995.
ДепманИ.Я., Виленкин Н.Я. За страницами учебника математики М., «Просвещение»1989.






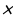 15см), масштабная линейка, ножницы
15см), масштабная линейка, ножницы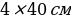 , изготовленные заранее кем-нибудь из кружковцев по заданию руководителя кружка. Для демонстрации необходимо иметь 3-4 такие «палочки». Затем учащиеся мастерят их сами. На рисунке показано, как можно сделать один комплект палочек.
, изготовленные заранее кем-нибудь из кружковцев по заданию руководителя кружка. Для демонстрации необходимо иметь 3-4 такие «палочки». Затем учащиеся мастерят их сами. На рисунке показано, как можно сделать один комплект палочек. 











 0
0 0
0

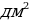 для изготовления разрезного квадрата, масштабная линейка, циркуль и карандаш.
для изготовления разрезного квадрата, масштабная линейка, циркуль и карандаш. ), который используется как шаблон. Затем по шаблону изготовляют разрезной квадрат из картона, составляют фигурки из частей квадрата («свеча», «наездник» и др.). Кто скорее сложит? Для образца вывешиваются силуэты фигурок без обозначения контуров составляющих частей.
), который используется как шаблон. Затем по шаблону изготовляют разрезной квадрат из картона, составляют фигурки из частей квадрата («свеча», «наездник» и др.). Кто скорее сложит? Для образца вывешиваются силуэты фигурок без обозначения контуров составляющих частей.














