Математика: Неравенства. Повторение на примерах из Якласс, Учи.ру, РЭШ, интерактивной рабочей тетради Skysmart

Повторение 9 класс

• Числа и вычисления.
• Алгебраические выражения.
• Уравнения и системы уравнений.
• Неравенства и системы неравенств .
• Последовательности и прогрессии.
• Функции и графики.
• Текстовые задачи.

Тесты в ЭШ

Интерактивная рабочая тетрадь

по алгебре

https://edu.skysmart.ru/homework/new

3   или в виде числового промежутка. x ∈(3;+∞) . Отметить множество решений неравенства на числовой прямой и записать ответ в виде числового промежутка. Решить неравенство: − 8 x   +11   Решение 1. Перенесём член   −3 x   в левую часть неравенства, а член   11  — в правую часть неравенства,   при этом   поменяем знаки на противоположные у   −3 x   и у   11 .   Тогда получим − 8 x +3 x − 5 x 2. Разделим обе части   неравенства   −5 x , т. е. мы перейдём к неравенству противоположного смысла.   Получим: − 5 x x −15:(−5) x 3.   x 3  — решение заданного неравенства. Ответ :   x 3 , или   x ∈(3;+∞) . " width="640"

Для записи решения можно использовать два варианта:   x 3  

или в виде числового промежутка.

x ∈(3;+∞) .

Отметить множество решений неравенства на числовой прямой и записать ответ в виде числового промежутка.

Решить неравенство:

− 8 x   +11  

Решение

1. Перенесём член   −3 x   в левую часть неравенства, а член   11  — в правую часть неравенства,   при этом   поменяем знаки на противоположные у   −3 x   и у   11 .   Тогда получим

− 8 x +3 x

− 5 x

2. Разделим обе части   неравенства   −5 x , т. е. мы перейдём к неравенству противоположного смысла.   Получим:

− 5 x

x −15:(−5)

x 3.

  x 3  — решение заданного неравенства.

Ответ :   x 3 , или   x ∈(3;+∞) .

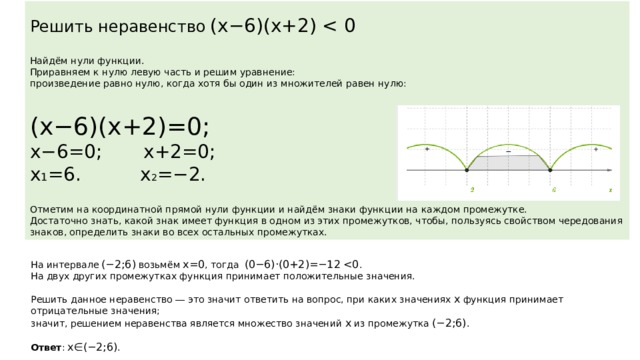
Решить неравенство   ( x −6)( x +2)

Найдём нули функции.

Приравняем к нулю левую часть и решим уравнение:

произведение равно нулю, когда хотя бы один из множителей равен нулю:

( x −6)( x +2)=0;

x −6=0; x +2=0;

x 1 =6. x 2 =−2.

Отметим на координатной прямой нули функции и найдём знаки функции на каждом промежутке.

Достаточно знать, какой знак имеет функция в одном из этих промежутков, чтобы, пользуясь свойством чередования знаков, определить знаки во всех остальных промежутках.

На интервале   (−2;6)   возьмём   x =0 , тогда    (0−6)⋅(0+2)=−12  

На двух других промежутках функция принимает положительные значения.

Решить данное неравенство — это значит ответить на вопрос, при каких значениях   x   функция   принимает отрицательные значения;

значит, решением неравенства является множество значений   x   из промежутка   (−2;6) .

Ответ :   x ∈(−2;6) .

3 3 x −2означает, что неравенства   2 x −13   и   3 x −2Значение переменной, при котором каждое из неравенств системы становится верным числовым неравенством, называют  решением системы неравенств. 1. Решив первое неравенство, получаем   2 x 4 |:2; x 2.   2. Решив второе неравенство, получаем   3 x x 3. Полученные промежутки отметим на оси координат. Для каждого возьмём свою штриховку (верхнюю или нижнюю). 4. Решение системы   неравенств —  это пересечение штриховок, т. е. промежуток,   на котором штриховки совпадают. Ответ:   ( 2;13 / 3 ) . " width="640"

Решить систему неравенств — 

это найти все её решения.

Система неравенств

состоит из нескольких неравенств с одной переменной.

Эти неравенства объединяются фигурной скобкой (так же, как и уравнения в системах уравнений).

Задача состоит в том, чтобы найти все общие решения заданных неравенств.

{

2 x −13

3 x −2

означает, что неравенства   2 x −13   и   3 x −2

Значение переменной, при котором каждое из неравенств системы становится верным числовым неравенством, называют  решением системы неравенств.

1. Решив первое неравенство, получаем

2 x 4 |:2;

x 2.

2. Решив второе неравенство, получаем

3 x

x

3. Полученные промежутки отметим на оси координат. Для каждого возьмём свою штриховку (верхнюю или нижнюю).

4. Решение системы   неравенств —  это пересечение штриховок, т. е. промежуток,   на котором штриховки совпадают.

Ответ:   ( 2;13 / 3 ) .

Неравенства называют равносильными,

если они имеют одинаковые решения, или в частности — если оба неравенства не имеют решений.

При решении неравенства данное неравенство заменяют более простым, но равносильным ему.

Такую замену называют равносильным преобразованием неравенства.

Практическая часть: Учи.ру и Якласс

Рациональным неравенством  

с одной переменной   x