Материал к урокам геометрии

Материалы к урокам геометрии в 7 классе по теме:

«Подобие треугольников.

Признаки подобия треугольников»

Содержание:

• Теоретический материал
• Признаки подобия треугольников
• Примеры решения задач
• Это интересно…
• Задачи для самостоятельного выполнения

Теоретический материал:

• Пропорциональные отрезки
• Определение подобных треугольников
• Отношение площадей подобных треугольников

Признаки подобия треугольников:

• I признак
• II признак
• III признак
• Подобие прямоугольных треугольников

Примеры решения задач:

• Задача 1
• Задача 2
• Задача 3

Пропорциональные отрезки.

Отношением отрезков АВ и CD называется отношение их длин, т. е.

АВ.

CD

Говорят, что отрезки АВ и CD пропор-циональны отрезкам А 1 В 1 и C 1 D 1 , если

АВ = CD.

А 1 В 1 C 1 D 1

Например, отрезки АВ и CD, длины которых равны 2 см и 1 см, пропорциональны отрезкам А 1 В 1 и C 1 D 1 , длины которых равны 3 см и 1,5 см.

В самом деле, АВ = CD = 2.

А 1 В 1 C 1 D 1 3

Определение подобных треугольников.

Пусть у двух треугольников АВС и А 1 В 1 С 1 соответствующие углы равны. В этом случае стороны АВ и А 1 В 1 , ВС и В 1 С 1 , СА и С 1 А 1 называются сходственными.

Два треугольника называются подобными , если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.

k

АВ ВС СА

А 1 В 1 В 1 С 1 С 1 А 1

Число k , равное отношению сходственных сторон треугольников, называется коэффициентом подобия .

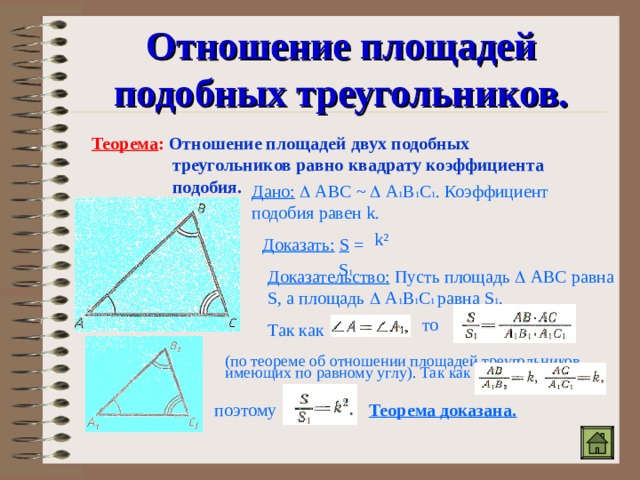
Отношение площадей подобных треугольников.

Теорема : Отношение площадей двух подобных

треугольников равно квадрату коэффициента

подобия.

Дано:  АВС ~  А 1 В 1 С 1 . Коэффициент подобия равен k .

k ²

Доказать: S =

S 1

Доказательство: Пусть площадь  АВС равна S , а площадь  А 1 В 1 С 1 равна S 1 .

Так как

то

(по теореме об отношении площадей треугольников, имеющих по равному углу). Так как

поэтому

Теорема доказана.

Первый признак подобия треугольников.

Теорема : Если два угла одного треугольника соответственно равны двум углам другого , то такие треугольники подобны.

Дано:  АВС,  А 1 В 1 С 1.

Доказать :  АВС ~  А 1 В 1 С 1 .

Доказательство: по теореме о сумме углов треугольника

Таким образом, углы  АВС

и, значит,

соответственно равны углам  А 1 В 1 С 1. Докажем, что стороны  АВС пропорциональны сходственным сторонам  А 1 В 1 С 1.

Т.к.

то

Из этих равенств следует, что

Аналогично, используя равенства

получаем

Итак, стороны  АВС пропорциональны сходственным сторонам  А 1 В 1 С 1. Теорема доказана.

Второй признак подобия треугольников.

Теорема: Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

Дано:  АВС,  А 1 В 1 С 1, , у которых

Доказать:  АВС ~  А 1 В 1 С 1 .

Доказательство: Достаточно доказать, что

Рассмотрим  АВС 2 , у которого

Треугольники АВС 2 и А 1 В 1 С 1 подобны по первому признаку подобия треугольников, поэтому

С другой стороны, по условию

Из этих двух равенств получаем АС = АС 2 .

 АВС и  АВС 2 равны по двум сторонам и углу между ними (АВ – общая сторона, АС=АС 2 и )

Отсюда следует, что

а так, как

Теорема доказана.

Третий признак подобия треугольников.

Теорема: Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

Дано:  АВС,  А 1 В 1 С 1, , у которых

Доказать:  АВС ~  А 1 В 1 С 1 .

Доказательство: Достаточно доказать, что

Рассмотрим  АВС 2 , у которого

Треугольники АВС 2 и А 1 В 1 С 1 подобны по первому признаку подобия треугольников, поэтому

Сравнивая эти равенства с равенствами, которые записаны в дано, получаем:

 АВС=  АВС 2 по трем сторонам. Отсюда следует, что

а так как

Теорема доказана.

Подобие прямоугольных треугольников.

Два прямоугольных треугольника подобны , если

• их катеты пропорциональны;

2) катет и гипотенуза одного треугольника пропорциональны катету и гипотенузе другого;

3) два угла одного треугольника равны двум углам другого треугольника.

Задача 1.

Основания трапеции равны 5 см и 8 см. Боковые стороны, равные 3,6 см и 3,9 см, продолжены до пересечения в точке М. Найдите расстояния от точки М до концов меньшего основания.

Дано: АВ CD – трапеция. AD=8 см, ВС=5 см, АВ = 3,6 см, CD = 3,9 см. АВ пересекает CD в точке М.

Найти: ВМ и СМ.

Решение:  AMD ~  ВМС по I признаку подобия треугольников (угол М – общий, угол MAD = углу МВС как односторонние при параллельных прямых ВС и AD и секущей АМ). Значит их сходственные стороны пропорциональны.

Пусть ВМ = x , тогда АМ = 3,6 + x . По определению подобных треугольников имеем

По свойству пропорций получим: 8 x = 5(3,6 + x). Отсюда получаем, что x = 6 . Значит ВМ = 6 см. Аналогично составим пропорцию для стороны МС:

По свойству пропорций получим: 8 x = 5(3,9 + x) . Отсюда получаем, что x = МС = 6,5 см.

Ответ: 6 см и 6,5 см.

Задача 2.

Стороны угла О пересечены параллельными прямыми АВ и CD . Докажите, что отрезки ОА и АС пропорциональны отрезкам ОВ и BD .

Дано: угол О, АВ II CD .

АВ пересекает угол О, CD пересекает угол О.

Доказать:

Доказательство: Проведем через точку А прямую АС 1 II BD (С 1 – точка пересечения этой прямой с прямой CD ). Тогда  ОАВ ~  АСС 1 по первому признаку подобия треугольников ( и

), следовательно,

Так как АС 1 = BD (по определению параллелограмма AC 1 DB ), то

Что и требовалось доказать.

Задача 3.

На одной из сторон данного угла А отложены отрезки АВ = 5 см и АС = 16 см. На другой стороне этого же угла отложены отрезки AD = 8 см и AF = 10 см. Подобны ли треугольники ACD и AFB ?

Дано: угол А. АВ = 5 см, АС = 16 см, AD = 8 см, AF = 10 см.

Проверить:  A С D ~  AFB ?

Решение: Используем II признак подобия треугольников. Угол А общий, значит нужно проверить пропорциональны ли сходственные стороны треугольников, заключающие этот угол А. По определению подобных треугольников должно выполняться следующее равенство:

Подставив данные мы получим

верное равенство:

Значит по второму признаку подобия треугольников  A С D ~  AFB .

Ответ: да.

Это интересно…

История учения о подобии фигур.

Искусство изображать предметы на плоскости с древних времен привлекало к себе внимание человека. Попытки таких изображений появились значительно раньше, чем возникла письменность. Еще в глубокой древности люди рисовали на скалах, сосудах и прочих предметах быта различные орнаменты, растения, животных. При этом человек стремился к тому, чтобы изображение правильно отражало естественную форму предмета.

Идея отношения и пропорции зародилась в глубокой древности. Одинаковые по форме, но различные по величине фигуры встречаются в вавилонских и египетских памятниках. В сохранившейся погребальной камере отца фараона Рамзеса II имеется стена, покрытая сетью квадратиков, с помощью которой на стену перенесены в увеличенном виде рисунки меньших размеров.

Учение о подобии фигур на основе теории отношений и пропорции было создано в Древней Греции в V-IV вв. до н. э. трудами Гиппократа Хиосского, Архита Тарентского, Евдокса Книдского и др. Оно изложено в VI книге «Начала» Евклида.

Символ, обозначающий подобие фигур, есть не что иное, как повернутая латинская буква S -первая буква в слове similis , что в переводе означает подобие.