Частота случайного события
1. Когда перед началом игры игроки хотят договориться, кто из них делает первый ход, то обычно подбрасывают монету. Так поступают потому, что выпадание орла или решки считается равновероятным и заинтересованные стороны имеют равные шансы.
Результат подбрасывания монеты, кнопки, игрального кубика, раскрытие книги наугад заранее предсказать нельзя, в каждом таком эксперименте результат зависит от случая, поэтому их называют экспериментами со случайными исходами или просто случайными экспериментами. Важно, что такие случайные эксперименты можно повторить многократно, причём в одних и тех же условиях.
Обычно многократные случайные эксперименты проводят, чтобы определить, насколько часто появляется интересующий нас результат. Например, как часто при подбрасывании монеты выпадает орёл или при одновременном подбрасывании двух кубиков выпадает двенадцать очков. Для этого по результатам серии экспериментов вычисляется частота наблюдаемого события.
Частотой случайного события в серии экспериментов называют отношение числа экспериментов, в которых это событие произошло, к общему числу экспериментов.
Частота показывает, какую часть от общего числа проведённых экспериментов составляют эксперименты, завершившиеся интересующим нас результатом.
Пусть в серии из N экспериментов интересующее нас событие произошло n раз, тогда его частота равна 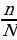 . Поскольку 0 ≤ n ≤ N, то частота выражается числом от 0 до 1. Если событие не произошло ни разу, т.е. n=0, то его частота в серии экспериментов равна 0. Если оно происходило каждый раз, то его частота равна 1.Частот у принято выражать также и в процентах.
. Поскольку 0 ≤ n ≤ N, то частота выражается числом от 0 до 1. Если событие не произошло ни разу, т.е. n=0, то его частота в серии экспериментов равна 0. Если оно происходило каждый раз, то его частота равна 1.Частот у принято выражать также и в процентах.
2. Представим, что монеты у наших игроков не оказалось, и один из них предложил подбросить кнопку. Можно ли считать такую замену справедливой, т.е. останутся ли шансы сторон равными? Давайте разберёмся.
Кнопка может упасть либо остриём вверх, либо остриём вниз. Чтобы ответить на вопрос, равны ли шансы этих исходов, надо много раз подбросить кнопку и собрать информацию о результатах. Если окажется, что при многократном подбрасывании кнопки частота падения кнопки остриём вниз и частота падения кнопки остриём вверх будут примерно равными, то это означает, что эти два исхода практически равновероятны и замена монеты на кнопку справедлива. Если же результаты будут отличаться, то эти два исхода равновероятными считать нельзя.
Проведем серию экспериментов по подбрасыванию кнопки с целью выявления закономерности падение кнопки остриём вниз и остриём вверх. Для этого работаем в парах, каждая из которых 100 раз побрасывает кнопку. Результаты заносим в таблицу. (Для экономии времени таблицу готовим заранее). Количество участников эксперимента определяем количеством учащихся в классе. Результаты всех испытаний заносим в общую таблицу. В первый столбец таблицы вносим результаты экспериментов, полученных одной парой. Далее каждый раз, заполняя следующий столбец таблицы, к результатам предыдущего столбца прибавляем результаты, полученные следующей парой учеников, и подсчитываем соответствующие частоты.
Возможные результаты. Перед вами таблица результатов, полученных одной из пар.
Таблица 1.
Из таблицы 1 видно, что частота падения кнопки остриём вниз в этой серии экспериментов равна 0,44, а частота падения кнопки остриём вверх равна 0,56.
Такие серии по 100 экспериментов в классе провели 10 пар учеников. Каждая пара получила свою таблицу результатов. Поскольку все кнопки из одной коробки можно считать одинаковыми, они свели результаты в одну таблицу.
Таблица 2.
| Число экспериментов | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 |
| Остриём вниз | Всего событий | 44 | 94 | 130 | 173 | 221 | 265 | 310 | 356 | 403 | 448 |
| Частота | 0,44 | 0,47 | 0,43 | 0,43 | 0,44 | 0,44 | 0,44 | 0,45 | 0,45 | 0,45 |
| Остриём вверх | Всего событий | 56 | 106 | 170 | 227 | 279 | 235 | 390 | 444 | 497 | 552 |
| Частота | 0,56 | 0,53 | 0,57 | 0,57 | 0,56 | 0,56 | 0,56 | 0,55 | 0,55 | 0,55 |
Из таблицы 2 видно, что при увеличении числа экспериментов частота каждого события выравнивается, ил, как говорят, стабилизируется. Частота события «остриём вверх» стабилизируется около числа 0,45, а частота события «остриём вверх» - около числа 0,55. Значит, шансы падения кнопки остриём вниз несколько меньше, чем остриём вверх.
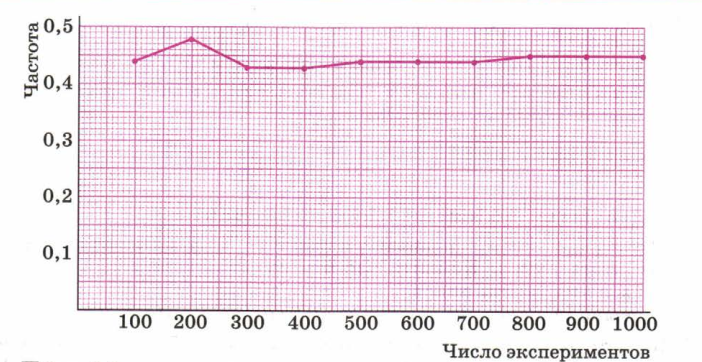
Стабилизация частоты будет нагляднее, если данные представить графически. Для этого каждая пара чисел таблицы ( число экспериментов – частота) отмечена точкой на координатной плоскости. Полученные точки соединены ломаной , которая при увеличении числа экспериментов становится практически горизонтальной прямой.
График зависимости частоты результата «остриём вниз» от числа экспериментов.
3. К экспериментам со случайными исходами относятся не только эксперименты, которые мы проводим сами. К ним относятся и самые разные опыты, испытания, наблюдения, измерения, проведённые кем-то другим, а также наблюдения за явлениями природы. Важно здесь то, что их результаты завияст от случая, но происходят каждый раз примерно в одних и тех же условиях. Надо лишь зафиксировать эти результаты. Случайными исходами таких испытаний являются, например, количество петухов и количество кур, вылупляющихся из каждой сотни яиц, температура воздуха в оин и тот же день в одном и том же месте, итоги еженедельной лотереи, результаты стрельбы по мишени, уровень весеннего разлива реки. В экспериментах со случыайными исходами уди вительно то, что, хотя проведении большого числа таких испытаний выявляются отчётливые закономерности. Частота соответствующих событий позволяет строить обоснованные прогнозы для решения задач, возникающих в жизни.
Ответьте на вопросы :
-
Что называют частотой случайного события?
-
Назовите два свойства случайного экспреимента
-
Монету подбросили 1000 раз, при этом 495 раз выпал орёл. Чему равна частота события « выпал орёл» в этой1 серии экспериментов?
Ответьте на вопросы по таблице 2:
-
Чему равна частота события «остриём вниз» после 300 испытаний? События «остриём вверх» после 500 испытаний?
-
После какого числа испытаний частота события «остриём вниз» стала равна 0,45?
-
Сколько раз кнопка упала остриём вверх у 6-й пары?
-
За лето на Черноморское побережье было 67 солнечных дней. Какова частота солнечных дней на побережье за лето? пасмурных дней? ( Используйте калькулятор)
Приведите примеры природных явлений, которые можно считать экспериментами со случайными исходами.
Примерное домашнее задание
1.В марте в городе родилось 2348 мальчиков и 2027 девочек. Найдите частоту рождения мальчиков и частоту рождения девочек в этом месяце. ( Используйте калькулятор)
2. Многолетняя проверка показала, что всхожесть семян огурцов определённого сорта составляет 90%. Посеяли 200 семян. Какое число проросших семян следует ожидать?
3. Готовясь к участию в теллеигре «Поле чудес», где по буквам отгадываются слова, олег задумался: «А какую букву стоит назвать первой, когда в слове ещё не угадано ни одной буквы?»
Понятно, что в такой ситуации выигрышная стратегия – начать игру с самой распространённой в русском языке буквы. Но как её определить? Чтобы помочь Олегу, 33 его одноклассника распределили между собой все буквы алфавита, взяли один и тот же текст и каждый посчитал, сколько раз в нём встречается его буква. Так они экспериментально определили самую распространённую букву русского языка.
Как вы думаете, что это за буква? Чтобы проверить свою догадку, проведите в классе такой же эксперимент, выбрав случайным образом текст из книги, которая есть у всех, например из учебника.







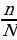 . Поскольку 0 ≤ n ≤ N, то частота выражается числом от 0 до 1. Если событие не произошло ни разу, т.е. n=0, то его частота в серии экспериментов равна 0. Если оно происходило каждый раз, то его частота равна 1.Частот у принято выражать также и в процентах.
. Поскольку 0 ≤ n ≤ N, то частота выражается числом от 0 до 1. Если событие не произошло ни разу, т.е. n=0, то его частота в серии экспериментов равна 0. Если оно происходило каждый раз, то его частота равна 1.Частот у принято выражать также и в процентах.