Материалы к уроку "Числовые наборы" (Статистика)

Числовые наборы.

Цель урока – сформировать у учащихся общее представление об описании числовых данных с помощью числовых характеристик – генеральная совокупность, выборка, ряд ). Учащиеся должны получить представление о том, что этих числовых характеристик много и способ описания данных в каждой задаче выбирается с учетом трех основных факторов:

• природа данных;

• цель исследования;

• сложившиеся традиции.

Что такое описательная статистика. Когда данные собраны и представлены в удобном виде, например, с помощью таблицы, возникает вопрос: где и как группируются эти данные – велики или малы значения и каков разброс (рассеивание) данных. Чтобы понять это, данные нужно описать подходящим образом. Для этого нужны описательные показатели или параметры: средние значения, наибольшее, наименьшее и другие. Поэтому раздел статистики, занимающийся описанием данных, называется описательной статистикой.

Наборы числовых данных – генеральная совокупность, выборка, ряд. Числовые данные могут быть устроены сложно. Они могут иметь разную природу и требовать разных способов описания. Например, бывают генеральные совокупности данных, бывают выборки, часто встречаются ряды.

1. Что такое генеральная совокупность? В ходе любого статистического исследования изучается какое-то свойство или несколько свойств большой группы однотипных объектов. Эта группа называется генеральная совокупность, т.е. главная. Она может быть задана перечислением всех своих элементов или указанием общего свойства, которое объединяет объекты в эту совокупность. Если изучаемая группа состоит из небольшого числа объектов ( например, школьный класс, в котором учится 20-30 человек), то все эти объекты можно указать явно. При выставлении отметок за ЕГЭ изучаемая группа составила 740 тыс. выпускников. Но использование современной компьютерной техники для сбора и хранения данных позволяет явно показать все объекты и в этом случае. В некоторых случаях трудно даже подсчитать общее количество объектов ( хотя совершенно ясно какие объекты входят в эту совокупность). Например, при изучении рыбных запасов в озере Байкал генеральная совокупность включает всех рыб, живущих в этом озере. Ясно, что подсчитать их число точно невозможно ( даже если не принимать в расчет непрерывное изменение числа рыб. Тем не менее, существуют статистические методы, которые позволяют решить эту задачу с разумной точностью. С еще более трудной проблемой сталкивается автомобильная компания, которая хочет понять, какие цвета предпочитают потенциальные покупатели новой модели автомобиля. В этом примере невозможно сразу точно сказать, какие люди входят в генеральную совокупность.

При статистическом исследовании чрезвычайно важно ясно понимать, о какой генеральной совокупности идет речь, т.е. какая группа объектов исследуется. Без этого нельзя правильно организовать сбор и обработку данных, правильно интерпретировать полученные результаты и выработать рекомендации по их правильному применению.

Чтобы проиллюстрировать понятия генеральной совокупности рассмотрим задачу 864 из учебника Математика. Алгебра. Функции. Анализ данных. Учебник для 8 класса общеобразовательных учреждений /Г.В. Дорофеев, С.Б.Суворова, Е.А. Бунимович и др.; под редакцией Г.В.Дорофеева.- Просвещение, 2018.:

« Маша, Саша, Катя, Лена, Ваня и Миша пошли в пиццерию. Ваня съел 5 кусков пиццы, Миша, Саша и Лена – по 3 куска, Катя – 2 куска, Маша – 1 кусок….»

В этом примере генеральная совокупность состоит из 6 «объектов»- школьников по именам Маша, Саша, Катя, Лена, Ваня, Миша. Для каждого школьника «измеряется» (фактически просто записывается) количество съеденных кусков пиццы - это будет в рассматриваемой задаче статистическая переменная. Обозначая количество съеденных пицц буквой W, можно записать:

W( Маша)=1, W(Саша)=3, W(Катя)=2, W(Лена)=3, W(Ваня)=5, W(Миша)=3.

Если каждому школьнику присвоить номер (например, в соответствии с тем, как они названы):

W₁= Маша, W₂= Саша, W₃= Катя, W₄= Лена, W₅= Ваня, W₆= Миша.

Соответственно, элементы генеральной совокупности можно записать так:

W₁= 1, W₂= 3, W₃= 2, W₄= 3, W₅= 5, W₆= 3.

Еще один пример. Предположим, что генеральная совокупность состоит из четырех учеников: Олеся, Даниил, Коля, Валерия, а интересующее нас свойство этих «объектов» - число решенных задач по геометрии, то Олеся решила 5 задач, Даниил -7, Коля – 3, Валерия – 5,

Обозначим число решенных задач буквой Х, то этот факт можно выразить следующим образом:

Х( Олеся)=5, Х(Даниил)= 7, Х(Коля)= 3, Х(Валерия)= 5.

или

Если каждому школьнику присвоить номер (например, в соответствии с тем, как они названы):

Х₁= Олеся, Х₂= Даниил, Х₃= Коля, Х₄= Валерия

Соответственно, элементы генеральной совокупности можно записать так:

Х₁= 5, Х₂= 7, Х₃= 3, Х₄= 5.

Таким образом, генеральная совокупность – это набор всех объектов, которые нужно исследовать.

2.Что такое выборка?

Чтобы проиллюстрировать понятия выборки рассмотрим пример из пункта «Выборочные исследования» учебника Алгебра.9 класс: учебник для общеобразовательных организаций /Г.В. Дорофеев, С.Б.Суворова, Е.А. Бунимович и др.; под редакцией Г.В.Дорофеева; Рос.акад.наук, Рос.акад. образования - Просвещение, 2014.:

Итак, составлена выборка из n учащихся, проведена контрольная работа, получены данные, которые подверглись анализу.

на основе этого можно построить диаграмму иметь наглядное представление о количестве решенных задач в контрольной работе:

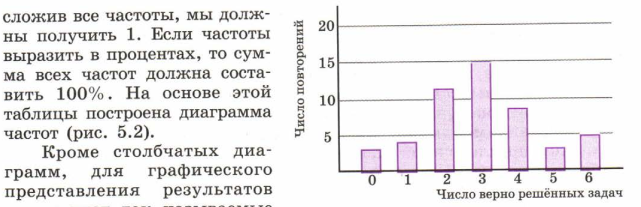
Вывод: Чтобы по выборке сделать достоверный или хотя бы правдоподобный вывод о всей совокупности, используются специальные выборочные методы.

Обсудите со школьниками, кому и зачем важно иметь сведения о результатах контрольной работы? Можно ли поменять местами порядок чисел в выборке?

Дата	Ср.цена	Изм.
29.10.2018	76,92	-1,08%
30.10.2018	76,32	-0,78%
31.10.2018	76,23	-0,12%
01.11.2018	72,75	-4,57%
02.11.2018	72,61	-0,19%
06.11.2018	72,1	-0,70%
07.11.2018	72,05	-0,07%
08.11.2018	70,69	-1,89%
09.11.2018	69,88	-1,15%
12.11.2018	70,94	1,52%

3.Что такое ряд? Предположим, что мы следим за некоторой изменчивой величиной. Например, за ценой на нефть. Цена нефти выражается в долларах за баррель(от английского barrel (бочка) – мера объема, равная примерно 159 л.). Каждый день фиксируется средняя цена за 1 баррель нефти марки Brent (нефтяная смесь из нескольких месторождений Северного моря. Цена на нефть марки Brent задает ценовой стандарт для стран Европы). В таблице показаны цены за 10 дней. Если данные каким- то образом упорядочены (по времени, по величине и т.п.), они образуют ряд.

Кому важно знать, как менялась цена на нефть во времени? Как можно использовать эту информацию? Можно ли в этой таблице поменять местами цены за разные дни?

Информация о ценах на нефть важна для нефтяников, экономистов и для правительства. Например, бюджет России в значительной степени формируется из доходов от продажи нефтепродуктов. Информация об изменении цен во времени – динамике – позволяет строить прогнозы, сравнения, принимать регулирующие решения. В этом примере важна не только сама цена, но и как она менялась день ото дня. Ряд – упорядоченный набор данных. Изменение порядка данных приведет к потере важной информации и даст нам другой ряд с другими свойствами.

Вывод. Выборки и ряды – специальные виды данных. Они требуют особых способов описания и обработки. Поэтому мы не будем специально изучать выборки и ряды, но все равно при изучении данных разной природы нам придется обсуждать, можно ли применить те или иные способы описания.

• Ряд данных – это ряд результатов каких-либо измерений.

Например:1) измерения роста человека

2) Измерения веса человека (животного)

3)Показания счетчика (электроэнергии, воды, тепла…)

4) Результаты в беге на стометровку

И т.д.

• Объемом ряда данных называется количество всех данных.

Например: дан ряд чисел 1; 3; 6; -4; 0. Объём его будет равен 5. Почему?

Задание на дом: ( раздать каждому)

- В институте сдавали зачет по высшей математике. В группе было 10 человек, и они получили соответствующие оценки: 3, 5, 5, 4, 4, 4, 3, 2, 4, 5.

Определите объём данного ряда.

Ответ: 10

2