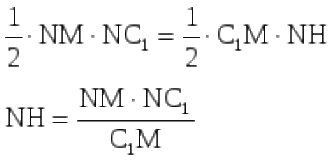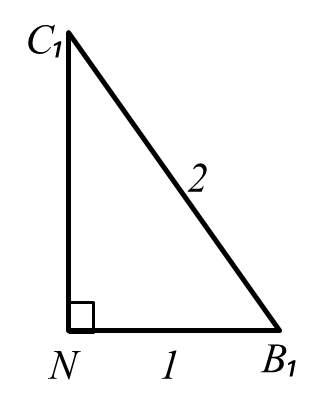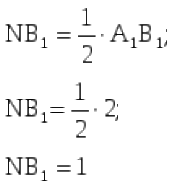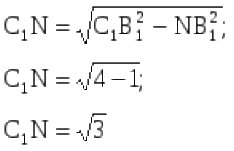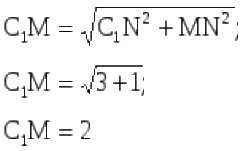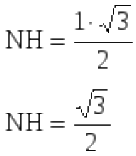Методическая разработка к уроку по теме «Нахождение расстояния от точки до плоскости, с использованием свойства прямой, параллельной плоскости»

Учитель математики МБОУ «СОШ№15» г. Курска Воскобойникова В.В.

Методическая разработка к уроку по теме

«Нахождение расстояния от точки до плоскости, с использованием свойства прямой, параллельной плоскости»

Расстояние между прямой и параллельной ей плоскостью.

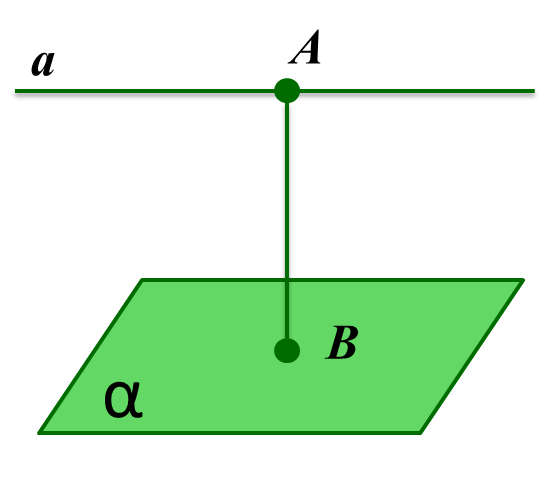
Если прямая параллельна плоскости, то все точки прямой равноудалены от этой плоскости.

В этом случае, расстояние между прямой и параллельной ей плоскостью есть расстояние от любой точки этой прямой до плоскости.

Выбираем на прямой, а произвольную точку А и находим расстояние от этой точки до плоскости α.

a ІІ α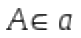

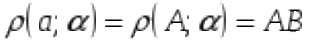
Задача

В правильной треугольной призме ABCA₁B₁C₁ сторона основания равна 2, а боковое ребро равно 1. Найдите расстояние от точки B₁ до плоскости ABC₁.

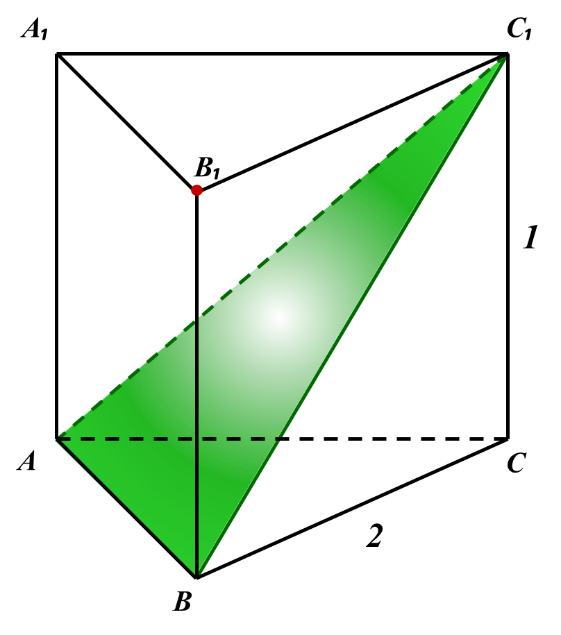
Дано:

ABCA₁B₁C₁- правильная треугольная призма

AB=BC=AC=2

CC₁=1

(ABC₁) - секущая плоскость

Найти: ρ (B₁; ABC₁)

Решение:

1) Поскольку А₁В₁ ІІ AB по свойству правильной призмы, значит А₁В₁ ІІ ABC₁ по признаку параллельности прямой и плоскости.

2) Следовательно, искомое расстояние от точки B₁ до плоскости ABC₁ есть расстояние от любой точки прямой A₁B₁ до плоскости ABC₁ (ведь все эти расстояния равны друг другу).

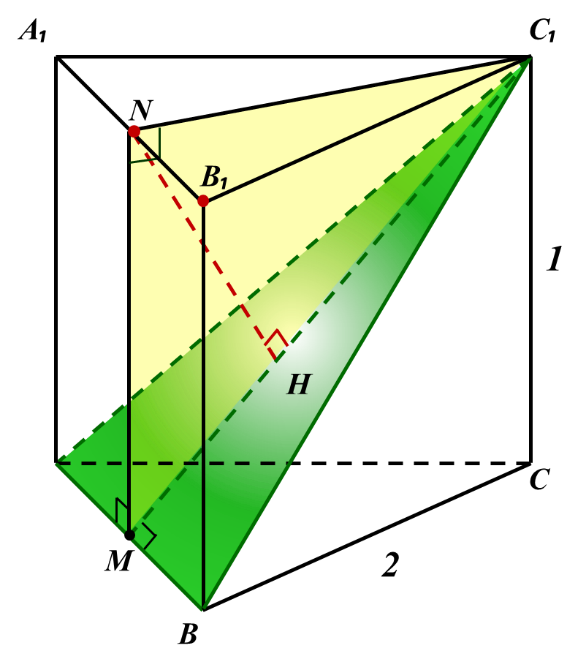
3) Поэтому мы можем выбрать наиболее удобную точку на прямой А₁В₁. Это точка N- середина А₁В₁. Найдем расстояние от точки N до плоскости ABC₁.

4) Пусть М- середина АВ.

5) Соединим N с М и N с С₁.

6) ∆АС₁В- равнобедренный с основанием АВ, АС₁=ВС₁– по свойству правильной призмы

С₁М- медиана.

7) В ∆MNC₁ проведем NH MC₁. И докажем, что NH АВC₁.

8) АВ С₁М, т.к. медиана С₁М в равнобедренном треугольнике ∆АВС₁ является и высотой.

АВ MN т.к. призма прямая. MN ∩ MC₁=M, MN  MNC₁, MC₁  MNC₁.

Значит, AB MNC₁ на основании признака перпендикулярности прямой и плоскости.

9) Следовательно, АВ перпендикулярна любой прямой лежащей в плоскости MNC₁, т.е. AB NH.

10) Итак, NHC₁M (построению) и NHAB (по доказанному) АВ ∩ МС₁=М, АВ АВС₁,

МС₁  АВС₁. По признаку перпендикулярности прямой и плоскости NH ABC₁.

11) Значит, длина NН- есть расстояние от точки N до плоскости АВС₁.

12) Найдем NН:

∆С₁NM- прямоугольный, т.к. призма прямая.

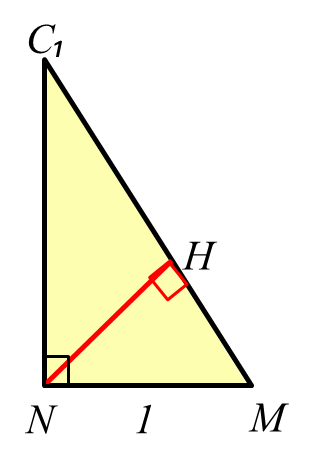
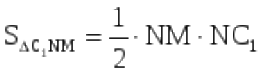
С другой стороны

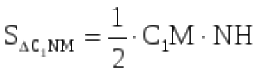
Из этих двух равенств получаем:

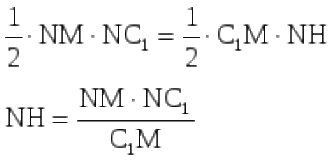
∆C₁NВ₁ - прямоугольный

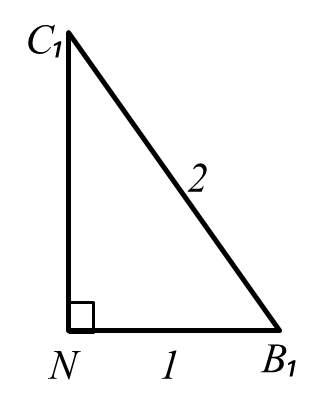
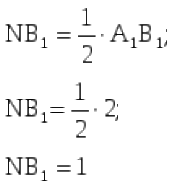
По теореме Пифагора:

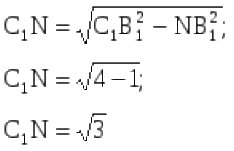
∆C₁NM- прямоугольный

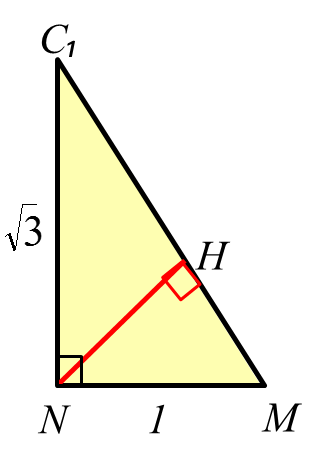
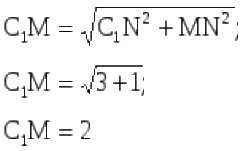
Так как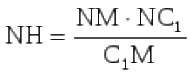

то

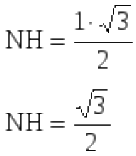
Ответ:

Второй способ вычисления NH:

∆С₁HN - прямоугольный

∆С₁NM- прямоугольный

Третий способ вычисления NH:

∆C₁HN ~ ∆C₁NM- по двум углам

Задача

В правильной шестиугольной пирамиде SABCDEF, сторона основания которой равна 1, а боковые ребра равны 2. Найдите расстояние от точки A до плоскости SDC.

Дано:

SABCDEF – правильная

шестиугольная пирамида

AB=BC=CD=DE=EF=FA=1

SC=SD=SE=SF=SA=SB=2

Найти: ρ (A; SDC)

Решение:

1) Поскольку AF ІІ DC по свойству правильного шестиугольника, значит AF ІІ SDC по признаку параллельности прямой и плоскости.

2) Следовательно, искомое расстояние от точки A до плоскости SDC есть расстояние от любой точки прямой AF до плоскости SDC (ведь все эти расстояния равны друг другу).

3) Поэтому мы можем выбрать наиболее удобную точку на прямой AF. Эта точка K – середина AF. Найдем расстояние от точки K до плоскости SDC.

4) KO – радиус вписанной окружности в правильный шестиугольник, то KO AF.

А так как AF ІІ DC и KOAF, значит, прямая KO DC на основании свойства параллельных прямых.

5) Точку пересечения KO и DC обозначим M, M – середина DC.

6) Проведем апофемы SM и SK.

7) В ∆SKM проведем KHSM. Докажем, что KH (SDC)

8) CDKM по доказанному CD SM, т.к. ∆SDC – равнобедренный, SM – медиана и высота.

KM ∩ SM=M, KM (SKM), SM (SKM)

Значит, CD KMS на основании признака перпендикулярности прямой и плоскости.

9) Значит CD перпендикулярна любой прямой лежащей в этой плоскости, т.е. CD KH.

10) А так как KHSM по построению и KH CD по доказанному, SM ∩ DC=M, SM (SDC),

DC  (SDC), то KH (SDC) на основании признака перпендикулярности прямой и плоскости.

11) Значит, длина KH – расстояние от точки K до плоскости SDC.

12) Найдем KH.

∆SOB – прямоугольный. OB – радиус описанной окружности.

R=, OB = 1

По теореме Пифагора

С другой стороны,

∆SMC – прямоугольный

По теореме Пифагора

Из равенств (1) и (2)

получаем:

Ответ:

Второй способ вычисления KH:

Запишем теорему косинусов для стороны KM в ∆SKM и найдем cos KSM,

∆SKM – равнобедренный:

Из основного тригонометрического тождества:

∆KHS -прямоугольный

Задачи для самостоятельного решения

1. В прямой треугольной призме ABCA₁B₁C₁ известны ребра: AB = AC = 5, BC = 6, AA₁ = 3. Найдите расстояние от точки C₁ до плоскости A₁BC. Ответ:

1. В правильной четырехугольной пирамиде SABCD (с вершиной S) сторона основания равна 6, а боковое ребро равно 5. Найдите расстояние от точки A до плоскости BCS.

Ответ:

1. В правильной шестиугольной пирамиде SABCDEF (с вершиной S) сторона основания равна 2, а боковое ребро равно . Найдите расстояние от точки A до плоскости BCS.

Ответ:

1. В правильной шестиугольной пирамиде SABCDEF (с вершиной S) сторона основания равна а боковое ребро равно. Найдите расстояние от точки A до плоскости CDS.

Ответ: