Методическая разработка цикла уроков по теме: "Алгебра логики"

Алгебра логики

Формы мышления и история развития алгебры логики

История логики насчитывает около двух с половиной тысячелетий. Первые учения о формах и способах мышления возникли в Древнем Китае и Индии. Основоположником формальной логики является Аристотель (384-322 гг. до н.э.) – древнегреческий философ, который впервые отделил логические формы мышления от его содержания.

Алгебра логики – наука об операциях, аналогичных математическим, над высказываниями или над объектами, которые могут принимать только два значения – «ИСТИНА» или «ЛОЖЬ».

В 1842 году английский математик Джорж Буль разработал математическую логику или алгебру логики , которую впоследствии стали называть «булевой алгеброй». Спустя 100 лет алгебра логики стала основой теории цифровых вычислительных машин, ее используют в компьютерной логике, электронике, в основе всех микропроцессорных операций.

Формы мышления и история развития алгебры логики

Многие философы и математики развивали отдельные положения логики и иногда даже намечали контуры современного исчисления высказываний, но ближе всех к созданию математической логики подошел уже во второй половине XVII века выдающийся немецкий ученый Готфрид Вильгельм Лейбниц (1646— 1716), указавший пути для перевода логики “из словесного царства, полного неопределенностей, в царство математики, где отношения между объектами или высказываниями определяются совершенно точно”. Лейбниц надеялся даже, что в будущем философы, вместо того чтобы бесплодно спорить, станут брать бумагу и вычислять, кто из них прав. При этом в своих работах Лейбниц затрагивал и двоичную систему счисления .   

Уже в XIX веке стало понятно, что система Буля хорошо подходит для описания электрических переключательных схем. Ток в цепи может либо протекать, либо отсутствовать, подобно тому, как утверждение может быть либо истинным, либо ложным. А еще несколько десятилетий спустя, уже в XX столетии, ученые объединили созданный Джорджем Булем математический аппарат с двоичной системой счисления, заложив тем самым основы для разработки цифрового электронного компьютера.

Логика – это наука о формах и способах мышления, рассуждений и доказательств.

Мышление осуществляется через понятия, высказывания и умозаключения.

Умозаключение – это форма мышления, с помощью которой из одного или нескольких простых высказываний (суждений) может быть получено новое сост авное высказывание (суждение).

Понятие – это форма мышления, выделяющая существенные и отличительные признаки объекта.

Высказывание – это формулировка в форме утверждения или отрицания об объекте и его свойствах. Высказывание может быть истинным или ложным.

Алгебра высказываний

Алгебра высказываний была разработана для того, чтобы определять истинность или ложность составных высказываний, не вникая в их содержание

Высказывание

• Высказывание – это форма мышления, в которой что-либо утверждается или отрицается о реальных предметах, их свойствах и отношениях между ними;

• Высказывание может быть либо истинно, либо ложно;

• Высказывания могут быть выражены с помощью естественных и формальных языков;

• Высказывания могут быть выражены только повествовательным предложением.

Примеры высказываний

Истинное высказывание: «Буква «А» - гласная».

Ложное высказывание: «Компьютер был изобретен в середине XIX века».

Какие из предложений являются высказываниями? Какие из высказываний истинные?

1. Какой длины эта лента? 2. Прослушайте сообщение. 3. Делайте утреннюю зарядку! 4. Назовите устройства ввода информации. 5. Кто отсутствует? 6. Париж – столица Англии. 7. Число 11 является простым. 8. 4+5=10 9. Без труда не вытащишь и рыбку из пруда. 10. Сложите числа 2 и 5. 11. Некоторые медведи живут на Севере. 12. Все медведи – бурые. 13. Чему равно расстояние от Москвы до Ленинграда? 14. Сумма углов треугольника – 180 градусов.

Не высказывание

Не высказывание

Не высказывание

Не высказывание

Не высказывание

Ложное высказывание

Истинное высказывание

Ложное высказывание

Истинное высказывание

Не высказывание

Истинное высказывание

Ложное высказывание

Не высказывание

Истинное высказывание

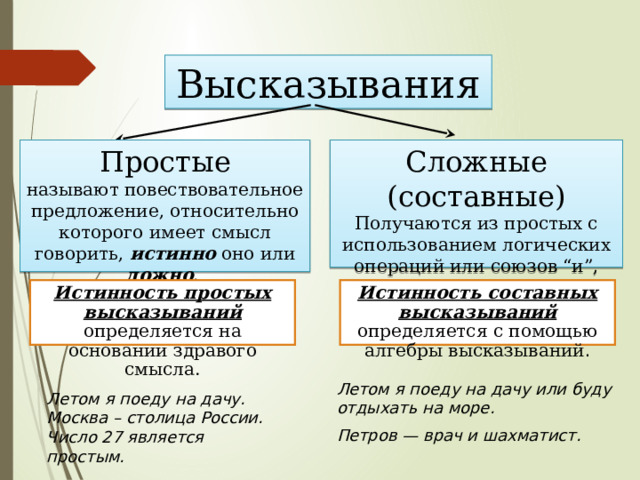
Высказывания

Простые

Сложные (составные)

называют повествовательное предложение, относительно которого имеет смысл говорить, истинно оно или ложно .

Получаются из простых с использованием логических операций или союзов “и”, “или”, “не”, “если то”.

Истинность простых высказываний определяется на основании здравого смысла.

Истинность составных высказываний определяется с помощью алгебры высказываний .

Летом я поеду на дачу или буду отдыхать на море.

Петров — врач и шахматист.

Летом я поеду на дачу.

Москва – столица России. Число 27 является простым.

Логические выражения

Логические переменные

Логические переменные – простые высказывания, содержащие только одну мысль.

Обозначаются буквами латинского алфавита: A, B, C…

Логические переменные могут принимать лишь два значения: «ИСТИНА» (1) или «ЛОЖЬ» (0)

Например , два простых высказывания:

А = «2 × 2 = 4» истина (1)

В = «2 × 2 = 5» ложь (0)

являются логическими переменными А и В

Логические константы

Логические константы – принимают 2 значения.

1

Истина

0

True

Ложь

False

В алгебре высказываний над логическими переменными (над высказываниями) можно производить определенные логические операции , в результате которых получаются новые высказывания

Логические операции

• Конъюнкция (логическое умножение, «И»)
• Дизъюнкция (логическое сложение, «ИЛИ»)
• Инверсия (логическое отрицание, «НЕ»)
• Импликация (логическое следование, «Если А , то В »)
• Эквивалентность (логическое равенство (тождество), « А тогда и только тогда, когда В »)
• Строгая дизъюнкция

(исключающее ИЛИ , неравнозначность, сумма по модулю 2)

Конъюнкция

Объединение двух или нескольких высказываний в одно с помощью союза «И» называется операцией логического умножения , или конъюнкцией.

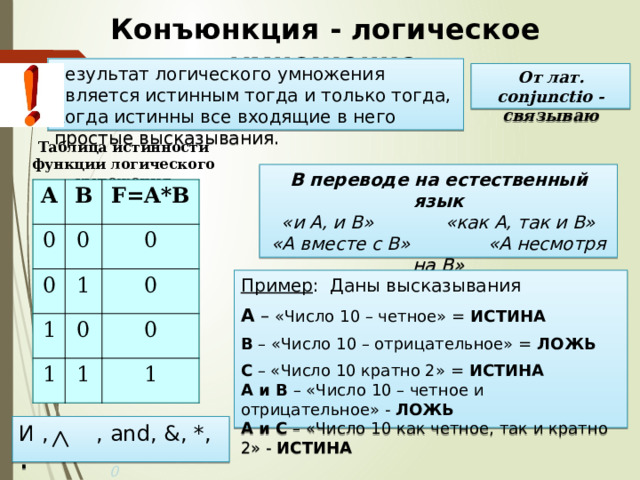
Конъюнкция - логическое умножение

Результат логического умножения является истинным тогда и только тогда, когда истинны все входящие в него простые высказывания.

От лат. conjunctio - связываю

Таблица истинности функции логического умножения

В переводе на естественный язык «и А, и В» «как А, так и В» «А вместе с В» «А несмотря на В» «А, в то время как В»

A

B

0

F=A*B

0

0

1

1

0

1

0

0

1

0

1

Пример : Даны высказывания

А – «Число 10 – четное» = ИСТИНА

В – «Число 10 – отрицательное» = ЛОЖЬ

С – «Число 10 кратно 2» = ИСТИНА А и В – «Число 10 – четное и отрицательное» - ЛОЖЬ А и С – «Число 10 как четное, так и кратно 2» - ИСТИНА

И , , and, &, *, ·

0

Дизъюнкция

Объединение двух или нескольких высказываний в одно с помощью союза «ИЛИ» называется операцией логического сложения , или дизъюнкцией.

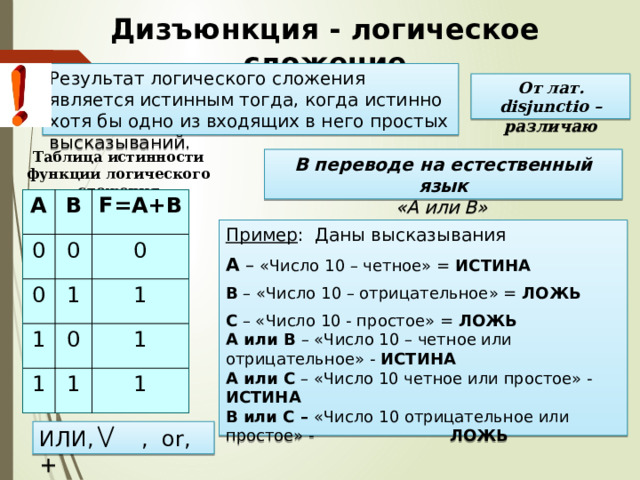
Дизъюнкция - логическое сложение

Результат логического сложения является истинным тогда, когда истинно хотя бы одно из входящих в него простых высказываний.

От лат. disjunctio – различаю

Таблица истинности функции логического сложения

В переводе на естественный язык «А или В»

A

B

0

F=A+B

0

0

1

0

1

1

1

0

1

1

1

Пример : Даны высказывания

А – «Число 10 – четное» = ИСТИНА

В – «Число 10 – отрицательное» = ЛОЖЬ

С – «Число 10 - простое» = ЛОЖЬ А или В – «Число 10 – четное или отрицательное» - ИСТИНА А или С – «Число 10 четное или простое» - ИСТИНА В или С – «Число 10 отрицательное или простое» - ЛОЖЬ

ИЛИ, , or, +

Инверсия

Присоединение частицы «НЕ» к высказыванию называется операцией логического отрицания , или инверсией.

Инверсия - логическое отрицание

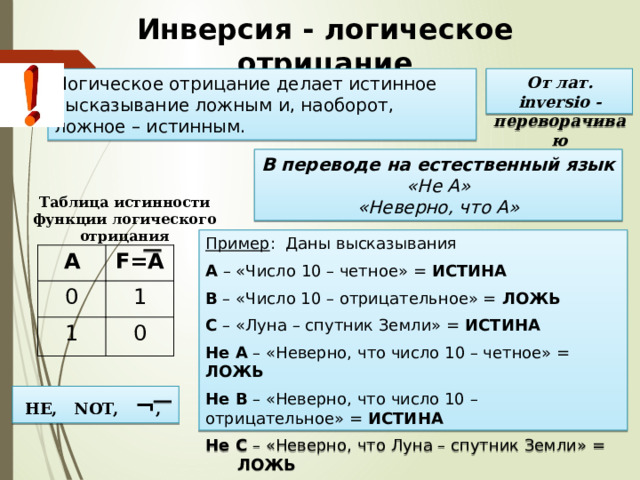
Логическое отрицание делает истинное высказывание ложным и, наоборот, ложное – истинным.

От лат. inversio - переворачиваю

В переводе на естественный язык «Не А» «Неверно, что А»

Таблица истинности функции логического отрицания

Пример : Даны высказывания

А – «Число 10 – четное» = ИСТИНА

В – «Число 10 – отрицательное» = ЛОЖЬ

С – «Луна – спутник Земли» = ИСТИНА

Не А – «Неверно, что число 10 – четное» = ЛОЖЬ

Не В – «Неверно, что число 10 – отрицательное» = ИСТИНА

Не С – «Неверно, что Луна – спутник Земли» = ЛОЖЬ

A

0

F=А

1

1

0

НЕ, NOT, ¬ ,

Импликация

Логическое следование (импликация) образуется соединением двух высказываний в одно с помощью оборота речи «если …, то …».

Импликация - логическое следование

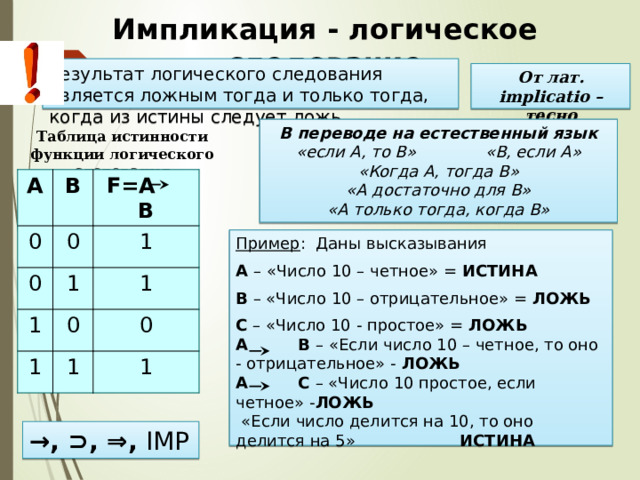
Результат логического следования является ложным тогда и только тогда, когда из истины следует ложь.

От лат. implicatio – тесно связывать

В переводе на естественный язык «если А, то В» «В, если А» «Когда А, тогда В» «А достаточно для В» «А только тогда, когда В»

Таблица истинности функции логического следования

A

B

0

F=A B

0

0

1

1

1

1

0

1

1

0

1

Пример : Даны высказывания

А – «Число 10 – четное» = ИСТИНА

В – «Число 10 – отрицательное» = ЛОЖЬ

С – «Число 10 - простое» = ЛОЖЬ А В – «Если число 10 – четное, то оно - отрицательное» - ЛОЖЬ А С – «Число 10 простое, если четное» - ЛОЖЬ «Если число делится на 10, то оно делится на 5» ИСТИНА

→ , ⊃, ⇒, IMP

Эквивалентность

Логическое равенство (эквивалентность) образуется соединением двух высказываний в одно с помощью оборота речи «… тогда и только тогда, когда …».

Эквивалентность - логическое равенство

Результат логического равенства является истинным тогда и только тогда, когда оба высказывания одновременно либо истинны, либо ложны.

От лат. aeguivalens – равноценное

Таблица истинности функции логического равенства

В переводе на естественный язык «А эквивалентно В» «А только тогда и только тогда, когда В»

A

B

0

F=A B

0

0

1

1

1

1

0

0

1

0

1

Пример : Даны высказывания

А – «Число 10 – четное» = ИСТИНА

В – «Число 10 – отрицательное» = ЛОЖЬ

С – «Число 10 - простое» = ЛОЖЬ А В – «Число 10 – четное, тогда и только тогда, когда оно - отрицательное» - ЛОЖЬ В С – «Число 10 такое же простое, как и отрицательное» ИСТИНА

≡ , , ~ , ⇔ , EQV

Строгая дизъюнкция

Строгая дизъюнкция - логическая операция, по своему применению максимально приближенная к грамматической конструкции «либо … либо …».

Строгая дизъюнкция

  Результат выполнения логической операции будет равен 1 (единице), если один из битов a или b равен 1 (единице), во всех остальных случаях, результат равен 0 (нулю).

Таблица истинности функции исключающее ИЛИ

A

B

0

F=A⊕B

0

0

1

0

1

1

1

0

1

1

0

Пример : Даны высказывания

А – «Я пойду в кино» = ИСТИНА

В – «Я пойду на каток» = ИСТИНА

С – «Я пойду в школу» = ЛОЖЬ

А ⊕ В – «Я пойду либо в кино либо на каток» - ЛОЖЬ А ⊕ С – «Я пойду либо в кино либо в школу» - ИСТИНА В ⊕ С – «Я пойду либо на каток либо в школу» - ИСТИНА

⊕ , XOR

Порядок действий

• Действия в скобках
• Отрицание
• Конъюнкция
• Дизъюнкция /Строгая дизъюнкция
• Импликация / Эквивалентность

=A) * (X3 «Точка Х не принадлежит интервалу [A;B]» (X=A) * (X4 «Неверно, что если дует ветер, то солнце светит только тогда, когда нет дождя.» В С В (С D) D – идет дождь " width="640"

Упражнения по записи высказываний в виде логических выражений

1

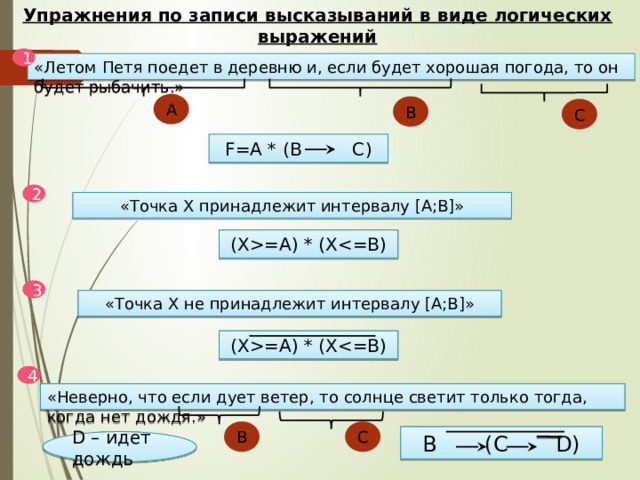
«Летом Петя поедет в деревню и, если будет хорошая погода, то он будет рыбачить.»

А

В

С

F=A * (B C)

2

«Точка Х принадлежит интервалу [A;B]»

(X=A) * (X

3

«Точка Х не принадлежит интервалу [A;B]»

(X=A) * (X

4

«Неверно, что если дует ветер, то солнце светит только тогда, когда нет дождя.»

В

С

В (С D)

D – идет дождь

Упражнения по записи высказываний в виде логических выражений

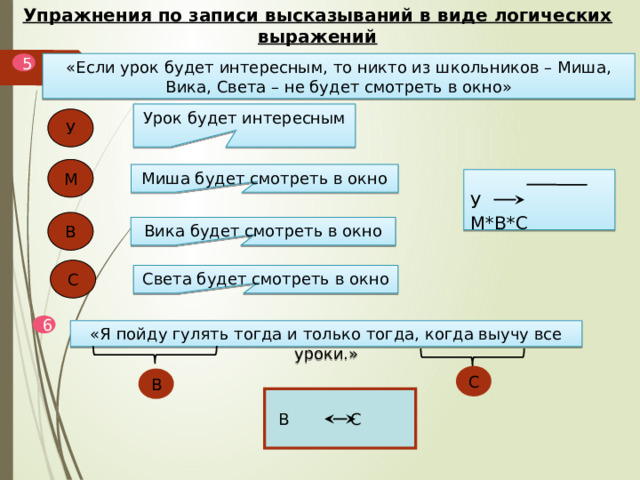
«Если урок будет интересным, то никто из школьников – Миша, Вика, Света – не будет смотреть в окно»

5

Урок будет интересным

У

М

Миша будет смотреть в окно

У М*В*С

В

Вика будет смотреть в окно

С

Света будет смотреть в окно

6

«Я пойду гулять тогда и только тогда, когда выучу все уроки.»

С

В

В С