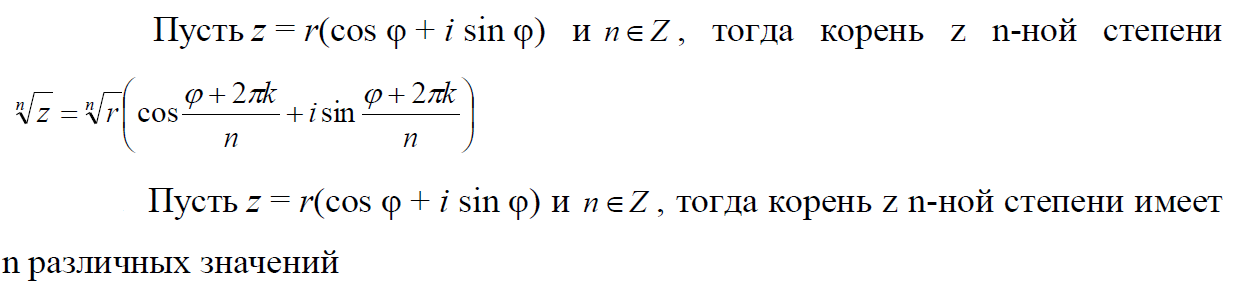Методическая разработка занятия по математике по теме «Действия над комплексными числами в тригонометрической форме»

Занятие 42. Тема «Действия над комплексными числами в тригонометрической форме»

План занятия:

1. Повторение основных понятий.

2. Действия над комплексными числами в тригонометрической форме.

1. Повторение основных понятий.

Комплексным числом z называется выражение вида z = x +iy, где х и у – действительные числа, а i – так называемая мнимая единица, i²= –1.

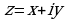Запись числа в виде называют алгебраической формой комплексного числа. Для того, чтобы перейти от алгебраической формы записи комплексного числа к тригонометрической форме, нужно найти его

модуль и аргумент.

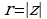Модуль однозначно определяется по формуле 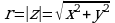. Например, . Аргумент 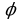определяется из формул

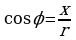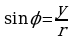, , . Тогда тригонометрическая форма записи комплексного числа .

1. Действия над комплексными числами в тригонометрической форме.

Примеры:

№1

№2

Задание для самостоятельного выполнения

№1. Вариант выполнения соответствует порядковому номеру.

Даны числа Z₁ и Z₂, найти Z₁ * Z₂, Z₁/ Z₂, Z₁⁵ и Z₂⁸

№3 Найти:

Выполненные задания отправить на адрес электронной почты преподавателя: [email protected]. Имя файла – фамилия студента и номер занятия. (например, Петров-42)