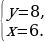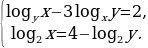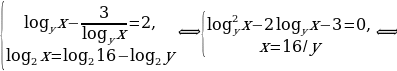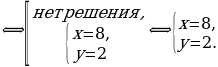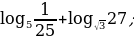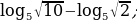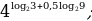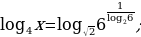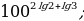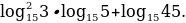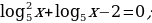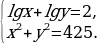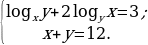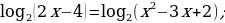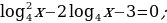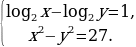МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕДЖДЕНИЕ
«ШКОЛА № 120 ГОРОДА ДОНЕЦКА»
Методические рекомендации на тему:
«Логарифмы. Логарифмические уравнения»
Выполнила:
учитель математики
Кориненко Е. В.
2021
Методические рекомендации на тему:
«Логарифмы. Логарифмические уравнения»
Цели:
- повторить, обобщить и систематизировать теоретический материал по теме
«Логарифмы. Логарифмические уравнения», обеспечить овладение всеми
обучащимися основными алгоритмическими приёмами решения логарифмов и
логарифмических уравнений;
- развивать мышление обучающихся, способности к само- и взаимоконтролю;
- формирование навыков поиска рациональных путей решения, самообразование.
- воспитывать сознательное отношение к изучению математики.
Понятие о логарифме числа.
Логарифм.
Задача нахождения показателя степени 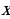 в примере
в примере  оказывается неразрешимой с применением известных шести математических действий. Определив тем не менее, что
оказывается неразрешимой с применением известных шести математических действий. Определив тем не менее, что  , записать решение этой задачи с помощью известных математических знаков невозможно.
, записать решение этой задачи с помощью известных математических знаков невозможно.
Н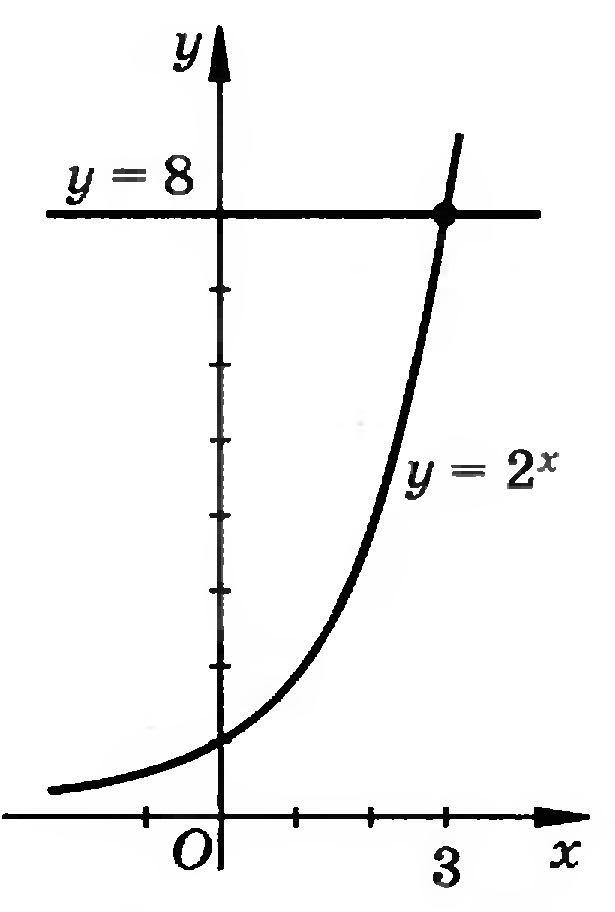 о эту задачу можно решить графическим способом. Для этого необходимо найти точки пересечения графиков
о эту задачу можно решить графическим способом. Для этого необходимо найти точки пересечения графиков  и
и 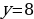 (рис. 1). Это точка, имеющая координаты (3; 8).
(рис. 1). Это точка, имеющая координаты (3; 8).
Графический способ иногда позволяет решить задачу, которую нельзя решить с помощью обычных математических приемов.
В общем виде рассмотренный пример будет иметь вид 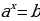 , где
, где 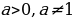 . Это уравнение не имеет решений при
. Это уравнение не имеет решений при 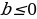 и имеет
и имеет
Рис.1 единственный корень 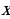 в случае
в случае  .
.
Этот корень называют логарифмом  по основанию
по основанию 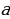 и обозначают
и обозначают 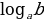 , то есть:
, то есть:
 . (1.1)
. (1.1)
Определение: Логарифмом числа  по основанию
по основанию 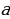 называется показатель
называется показатель
степени, в которую нужно возвести основание 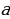 , чтобы
, чтобы
получить число  .
.
Подставим в выражение 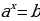 в качестве
в качестве 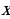 его представление по (1.1). Тогда получим
его представление по (1.1). Тогда получим
 . (1.2)
. (1.2)
Это равенство называют основным логарифмическим тождеством. Оно справедливо при 
Пример 1.
Найдем значение: а) 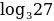 ; б)
; б)  .
.
а) Заметим, что  , т.е. для того, чтобы получить число 27, надо 3 возвести в третью степень. Следовательно,
, т.е. для того, чтобы получить число 27, надо 3 возвести в третью степень. Следовательно,  .
.
б) Заметим, что  , поэтому
, поэтому 
Пример 2.
Найдем логарифм числа 64 по основанию 4.
Заметим, что  Поэтому по определению логарифма
Поэтому по определению логарифма 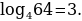
Пример 3.
Найдем 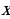 , такое, что: а)
, такое, что: а) 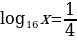 ; б)
; б) 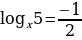 .
.
Воспользуемся основным логарифмическим тождеством:
а) 
б)  т.е.
т.е. 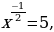 откуда
откуда 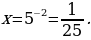
2. Свойства логарифмов.
Рассмотрим свойства логарифмов, которые используются при выполнении различных преобразований и решении уравнений.
При любом 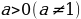 и любых положительных
и любых положительных 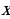 и
и 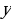 выполняются равенства:
выполняются равенства:
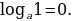

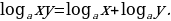
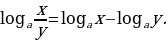
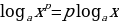 для любого действительного p.
для любого действительного p.
Для доказательства правила 3 воспользуемся основным логарифмическим тождеством:
 (1.3)
(1.3)
Перемножая почленно эти равенства, получаем:

т.е.  Следовательно, по определению логарифма
Следовательно, по определению логарифма 
Правило 4 докажем вновь с помощью равенств (1.3):
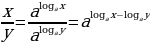 ,
,
Следовательно, по определению  .
.
Для доказательства правила 5 воспользуемся тождеством 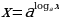 , откуда
, откуда  Следовательно, по определению
Следовательно, по определению 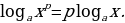
Отметим, что если  , то
, то 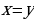 , т.е. если логарифмы двух чисел по одному и тому же основанию равны, то равны и сами числа.
, т.е. если логарифмы двух чисел по одному и тому же основанию равны, то равны и сами числа.
Пример 4.
Найдем значение выражения 
Пользуясь третьим свойством логарифмов, преобразуем данное выражение: 
Следовательно, 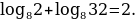
Пример 5.
Найдем значение выражения 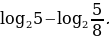
Пользуясь четвертым свойством логарифмов, преобразуем данное выражение: 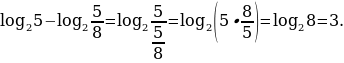
Следовательно, 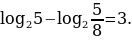
Пример 6.
Найдем 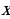 , если
, если 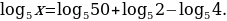
Сначала преобразуем правую часть данного равенства, пользуясь основными свойствами логарифмов:

т.е.  и поэтому
и поэтому 
Пример 7.
Найдем 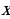 , если
, если
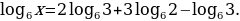
Сначала преобразуем правую часть данного равенства, пользуясь основными свойствами логарифмов:

т.е.  и поэтому
и поэтому 
Пример 8.
Найдем значение выражения 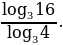
Пользуясь пятым свойством логарифмов, преобразуем данное выражение:
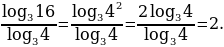
Следовательно, 
Пример 9.
Найдем значение выражения 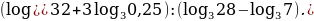
Пользуясь основными свойствами логарифмов, преобразуем данное выражение:
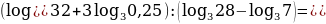
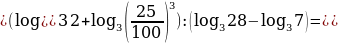
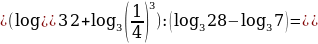
 =
=

Логарифмирование.
Действие нахождения логарифма числа называют логарифмированием. Если одночленное выражение составлено из положительных чисел с применением действий умножения, деления, возведения в степень и извлечения корня, то логарифм такого выражения вычисляется с использованием основных свойств логарифмов (1-5).
Пример 10.
Прологарифмируем по основанию 3 при  выражения:
выражения:
а)  ; б)
; б) 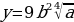 .
.
а) Имеем
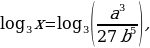

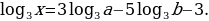
б) Имеем

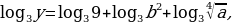
 .
.
Потенцирование.
Действие, обратное логарифмированию, называется потенцированием.
Этим действием с использованием основных свойств логарифмов (1-5) по логарифму выражения восстанавливается само выражение. Приведем примеры таких действий.
Пример 11.
Определить 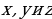 , если:
, если:
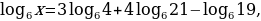


Решение.
Имеем:
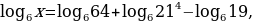

следовательно, 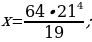

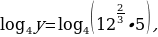
следовательно, 
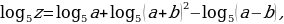
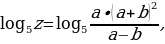
следовательно, 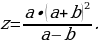
Десятичные и натуральные логарифмы.
Десятичным логарифмом числа называется логарифм этого числа по основанию 10. Такой логарифм записывается следующим образом:

Десятичные логарифмы чисел, составляющих некоторую степень числа 10, легко вычисляются, например,
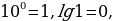
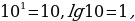


Логарифмы остальных чисел определяются либо с помощью таблиц, имеющихся в различных справочниках, либо с применением микрокалькуляторов.
Натуральным логарифмом числа называется логарифм этого числа по основанию е, где е – иррациональное число, приближенно равное 2, 718. Логарифм числа по основанию е записывается следующим образом:
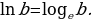
Заметим,  (по основным свойствам логарифмов).
(по основным свойствам логарифмов).
Логарифмические тождества.
Выведем формулу перехода от одного основания логарифма к другому основанию:

(Эта формула верна, если обе ее части имеют смысл, т.е. при 
По правилу логарифмирования степени и основному логарифмическому тождеству получаем:
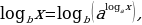
откуда
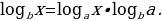
Разделив обе части полученного равенства на 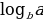 , приходим к нужной формуле.
, приходим к нужной формуле.
Пример 12.
Вычислить: а)  ; б)
; б)  .
.
Решение.
а) 
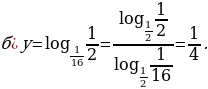
Докажем тождество
 (1.4)
(1.4)
Из основного логарифмического тождества (1.2)

иначе
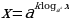 .
.
Прологарифмировав это равенство по основанию 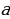 , получим:
, получим:

Из чего и следует тождество (1.4).
Пример 13.
Приведем  к основанию 2. По (1.4):
к основанию 2. По (1.4):

Любой логарифм можно представить в виде отношения двух логарифмов, взятых по одному и тому же основанию, т.е.
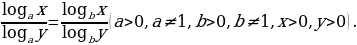 (1.5)
(1.5)
Из формулы перехода от одного основания логарифма к другому основанию следует, что
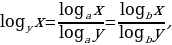
что и требовалось доказать.
Докажем тождество
 (1.6)
(1.6)
Пусть 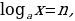 тогда
тогда  ; возведем это равенство в степень
; возведем это равенство в степень 

откуда 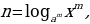 из чего и следует (1.6).
из чего и следует (1.6).
Пример 14.
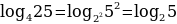 .
.
Логарифмические уравнения. Системы логарифмических уравнений.
Логарифмические уравнения.
Уравнение, содержащее переменную под знаком логарифма или в основании логарифма, называется логарифмическим. Проиллюстрируем различные способы решения таких уравнений с помощью следующих примеров:
Пример 1.
Решим уравнение 
Данному уравнению удовлетворяют те значения 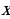 , для которых выполнено равенство
, для которых выполнено равенство  . Мы получили квадратное уравнение
. Мы получили квадратное уравнение  корни которого равны 1 и -5. Следовательно, числа 1 и -5 – решения данного уравнения.
корни которого равны 1 и -5. Следовательно, числа 1 и -5 – решения данного уравнения.
Ответ: -5; 1.
Пример 2.
Решим уравнение 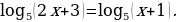
Это уравнение определено для тех значений 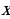 , при которых выполнены неравенства
, при которых выполнены неравенства  Для этих
Для этих 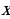 данное уравнение равносильно уравнению
данное уравнение равносильно уравнению 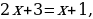 из которого находим
из которого находим  Число
Число  не удовлетворяет, однако, неравенству
не удовлетворяет, однако, неравенству  Следовательно, данное уравнение корней не имеет.
Следовательно, данное уравнение корней не имеет.
Это же уравнение можно решить иначе. Переходя к следствию данного уравнения 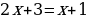 , находим, что
, находим, что  . Как всегда, при неравносильных преобразованиях уравнений найденное значение необходимо проверить подстановкой в исходное уравнение. В данном случае получаем, что равенство
. Как всегда, при неравносильных преобразованиях уравнений найденное значение необходимо проверить подстановкой в исходное уравнение. В данном случае получаем, что равенство  неверно (оно не имеет смысла).
неверно (оно не имеет смысла).
Ответ: нет корней.
Пример 3.
Решим уравнение 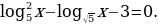
Перейдем во втором слагаемом к основанию 5 и сделаем замену переменной 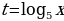 , тогда
, тогда

Теперь данное уравнение перепишется в виде
 Корни этого квадратного уравнения 3 и -1. Решая уравнение замены
Корни этого квадратного уравнения 3 и -1. Решая уравнение замены  и
и 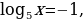 находим
находим 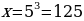 и
и 
Ответ: 0,2; 125.
Пример 4.
Решим уравнение 
Решение данного уравнения сводится к решению системы

Решением является 
Ответ: 64.
Пример 5.
Решим уравнение 
Учитывая, что  потенцируем:
потенцируем:


Данной системе удовлетворяет единственное решение 
Ответ: 4.
Пример 6.
Решим уравнение 
Данное уравнение преобразуем к квадратному, делаем замену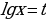 , тогда получим
, тогда получим  , D =
, D =  = 4
= 4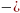
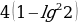 = 4
= 4 получим:
получим: 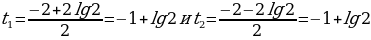 , тогда получим
, тогда получим
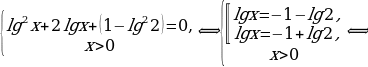

Корнями исходного уравнения являются 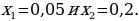
Ответ: 0,05; 0,2.
Пример 7.
Решим уравнение 
Логарифмируя обе части уравнения по основанию 10 получим уравнение:
 и решая затем полученное квадратное уравнение, находим
и решая затем полученное квадратное уравнение, находим

Исходному уравнению удовлетворяют корни 
Ответ: 0,1; 100.
Системы логарифмических уравнений.
Решение систем логарифмических уравнений основано на свойствах логарифмических функций.
Пример 8.
Решим систему уравнений
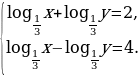
По свойствам логарифмов получаем, причем 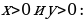
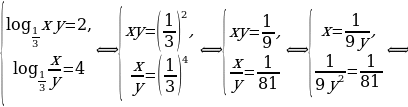
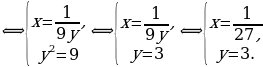
Ответ: 
Пример 9.
Решим систему уравнений
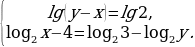
Первое уравнение системы равносильно уравнению  а второе – уравнению
а второе – уравнению  причем
причем 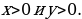
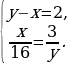
Подставляя 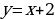 в уравнение
в уравнение 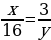 , получим
, получим 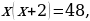 откуда
откуда 

Но так как 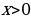 , то
, то  и
и 
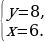
Ответ: (6;8).
Пример 10.
Решим систему уравнений
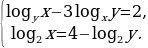
Здесь 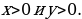 Имеем
Имеем
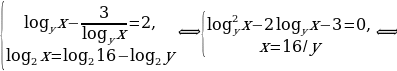

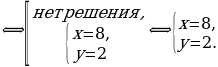
Ответ: (8;2).
Итог:
Самостоятельная работа № 1.
Тема работы: Логарифм. Свойства логарифмов.
Вариант 1.
Вычислите:
а) 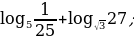
б) 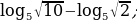
в) 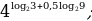
г) 
2. Найдите значение 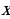 , если:
, если:
а) 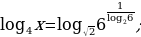
б) 
3. Сравните числа:
а) 
б) 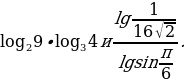
4. Найдите значение выражения:
а) 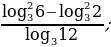
б) 
Вариант 2.
Вычислите:
а) 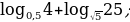
б) 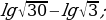
в) 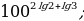
г) 
2. Найдите значение 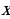 , если:
, если:
а) 
б) 
3. Сравните числа:
а) 
б) 
4. Найдите значение выражения:
а) 
б) 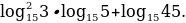
Самостоятельная работа № 2.
Тема работы: Логарифмические уравнения, неравенства и системы.
Вариант 1.
Решите уравнения:
а) 
б) 
в) 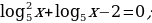
г) 
2. Решите системы:
а) 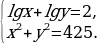
б) 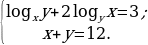
Вариант 2.
Решите уравнения:
а) 
б) 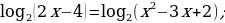
в) 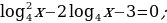
г) 
2. Решите системы:
а) 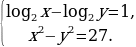
б) 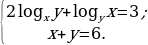







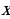 в примере
в примере  оказывается неразрешимой с применением известных шести математических действий. Определив тем не менее, что
оказывается неразрешимой с применением известных шести математических действий. Определив тем не менее, что  , записать решение этой задачи с помощью известных математических знаков невозможно.
, записать решение этой задачи с помощью известных математических знаков невозможно. о эту задачу можно решить графическим способом. Для этого необходимо найти точки пересечения графиков
о эту задачу можно решить графическим способом. Для этого необходимо найти точки пересечения графиков  и
и 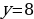 (рис. 1). Это точка, имеющая координаты (3; 8).
(рис. 1). Это точка, имеющая координаты (3; 8).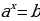 , где
, где 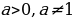 . Это уравнение не имеет решений при
. Это уравнение не имеет решений при 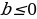 и имеет
и имеет  .
. по основанию
по основанию 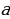 и обозначают
и обозначают 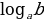 , то есть:
, то есть: . (1.1)
. (1.1) . (1.2)
. (1.2)
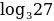 ; б)
; б)  .
. , т.е. для того, чтобы получить число 27, надо 3 возвести в третью степень. Следовательно,
, т.е. для того, чтобы получить число 27, надо 3 возвести в третью степень. Следовательно,  .
. , поэтому
, поэтому 
 Поэтому по определению логарифма
Поэтому по определению логарифма 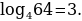
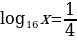 ; б)
; б) 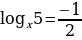 .
.
 т.е.
т.е. 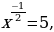 откуда
откуда 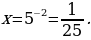
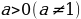 и любых положительных
и любых положительных 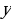 выполняются равенства:
выполняются равенства: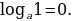

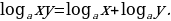
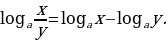
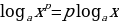 для любого действительного p.
для любого действительного p. (1.3)
(1.3)
 Следовательно, по определению логарифма
Следовательно, по определению логарифма 
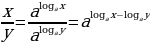 ,
,  .
. 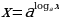 , откуда
, откуда  Следовательно, по определению
Следовательно, по определению 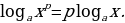
 , то
, то 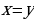 , т.е. если логарифмы двух чисел по одному и тому же основанию равны, то равны и сами числа.
, т.е. если логарифмы двух чисел по одному и тому же основанию равны, то равны и сами числа.

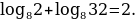
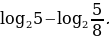
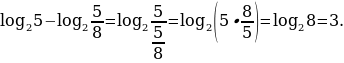
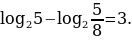
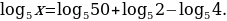

 и поэтому
и поэтому 
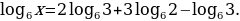

 и поэтому
и поэтому 
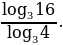
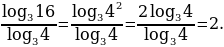

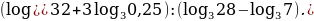
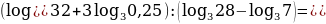
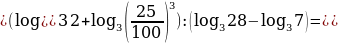
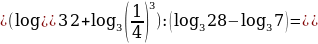
 =
=
 выражения:
выражения: ; б)
; б) 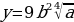 .
.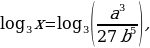

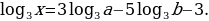

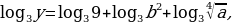
 .
.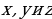 , если:
, если: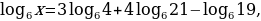


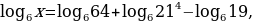

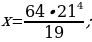

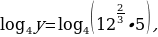

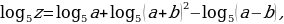
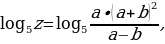
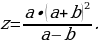

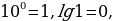
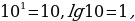


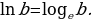
 (по основным свойствам логарифмов).
(по основным свойствам логарифмов).

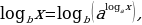
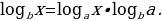
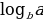 , приходим к нужной формуле.
, приходим к нужной формуле.  ; б)
; б)  .
.
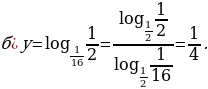
 (1.4)
(1.4)
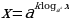 .
.
 к основанию 2. По (1.4):
к основанию 2. По (1.4):
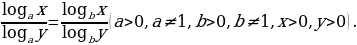 (1.5)
(1.5)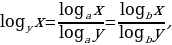
 (1.6)
(1.6)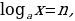 тогда
тогда  ; возведем это равенство в степень
; возведем это равенство в степень 

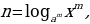 из чего и следует (1.6).
из чего и следует (1.6).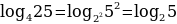 .
.
 . Мы получили квадратное уравнение
. Мы получили квадратное уравнение  корни которого равны 1 и -5. Следовательно, числа 1 и -5 – решения данного уравнения.
корни которого равны 1 и -5. Следовательно, числа 1 и -5 – решения данного уравнения.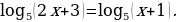
 Для этих
Для этих 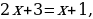 из которого находим
из которого находим  Число
Число  не удовлетворяет, однако, неравенству
не удовлетворяет, однако, неравенству  Следовательно, данное уравнение корней не имеет.
Следовательно, данное уравнение корней не имеет.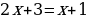 , находим, что
, находим, что  неверно (оно не имеет смысла).
неверно (оно не имеет смысла).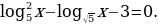
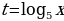 , тогда
, тогда 
 Корни этого квадратного уравнения 3 и -1. Решая уравнение замены
Корни этого квадратного уравнения 3 и -1. Решая уравнение замены  и
и 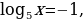 находим
находим 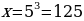 и
и 




 потенцируем:
потенцируем:



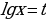 , тогда получим
, тогда получим  , D =
, D =  = 4
= 4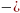
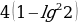 = 4
= 4 получим:
получим: 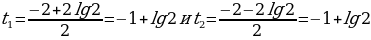 , тогда получим
, тогда получим 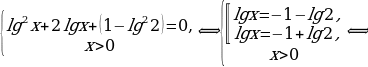

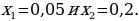

 и решая затем полученное квадратное уравнение, находим
и решая затем полученное квадратное уравнение, находим

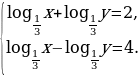
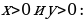
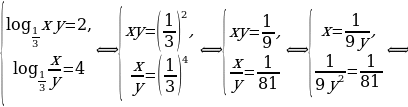
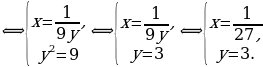

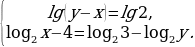
 а второе – уравнению
а второе – уравнению  причем
причем 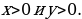
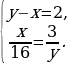
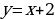 в уравнение
в уравнение 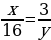 , получим
, получим 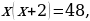 откуда
откуда 

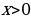 , то
, то  и
и