ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ, НАУКИ И МОЛОДЕЖНОЙ ПОЛИТИКИ
ВОРОНЕЖСКОЙ ОБЛАСТИ
--------------------------------------------
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВОРОНЕЖСКОЙ ОБЛАСТИ
«БОГУЧАРСКИЙ МНОГОПРОФИЛЬНЫЙ КОЛЛЕДЖ»
ГБПОУ ВО «БМК»
МЕТОДИЧЕСКИЕ указания по выполнению
практических работ по дисциплине
«Дискретная математика»
Для студентов 3 курсов по специальности СПО
09.02.01 Компьютерные системы и комплексы
Богучар - 2018
Составитель Литвинова Алёна Александровна
Методические указания по выполнению практических работ по дисциплине «Дискретная математика»: для студентов 3 курсов для специальности 09.02.01 «Компьютерные системы и комплексы»;
Методические указания разработаны в соответствии с рабочей программой по дискретной математике.
Аннотация:
Методические указания представляют собой разработку практических занятий по учебной дисциплине «Дискретная математика» Практические занятия представляют собой, занятия по выполнению различных заданий, образцы которых были даны на теории. В итоге у каждого студента должен быть выработан определенный профессиональный подход к решению каждой задачи.
Методические указания предназначены для студентов и содействуют выработке умений и навыков применения знаний, полученных на теории и в ходе практической работы.
Содержание
1. Цели и задачи дисциплины – требования к результатам освоения дисциплины;
2. Пояснительная записка;
3.Методические указания по проведению практической работы № 1:
«Теория множеств»;
4. Методические указания по проведению практической работы № 2:
«Графы»;
5. Методические указания по проведению практической работы № 3:
«Матлогика»;
6.Методические указания по проведению практической работы № 4: «Логика предикатов»;
7. Методические указания по проведению практической работы № 5:
«Конечные автоматы».
1.Цели и задачи дисциплины – требования к результатам освоения дисциплины:
В результате освоения дисциплины обучающийся должен уметь:
формулировать задачи логического характера и применять средства математической логики для их решения;
применять законы алгебры логики;
определять типы графов и давать их характеристики;
строить простейшие автоматы.
В результате освоения дисциплины обучающийся должен знать:
основные понятия и приемы дискретной математики;
основные понятия теории множеств, теоретико - множествнные операции и их связь с логическими операциями;
основные понятия теории графов, характеристики и виды графов;
логические операции, формулы логики, законы алгебры логики;
логика предикатов, бинарные отношения и их виды; элементы теории отображений и алгебры подстановок;
элементы теории автоматов.
Техник по компьютерным системам должен обладать общими компетенциями, включающими в себя способность:
ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.
ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.
ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.
ОК 5. Использовать информационно-коммуникационные технологии в профессиональной деятельности.
ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.
ОК 7. Брать на себя ответственность за работу членов команды (подчиненных), результат выполнения заданий.
ОК 8. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.
ОК 9. Ориентироваться в условиях частой смены технологий в профессиональной деятельности.
Техник по компьютерным системам должен обладать профессиональными компетенциями, соответствующими видам деятельности:
Проектирование цифровых устройств.
ПК 1.1. Выполнять требования технического задания на проектирование цифровых устройств.
ПК 1.3. Использовать средства и методы автоматизированного проектирования при разработке цифровых устройств.
2. Пояснительная записка
Практическое занятие - это форма организации учебного процесса, предполагающая выполнение обучающимися по заданию и под руководством преподавателя одной или нескольких практических работ.
Дидактическая цель практических работ - формирование у обучающихся профессиональных умений, а также практических умений, необходимых для изучения последующих учебных дисциплин, а также подготовка к применению этих умений в профессиональной деятельности.
Так, на практических занятиях по дискретной математике у обучающихся формируется умение решать задачи, которое в дальнейшем должно быть использовано для решения профессиональных задач по специальным дисциплинам.
В ходе практических работ обучающиеся овладевают умениями пользоваться информационными источниками, работать с нормативными документами и инструктивными материалами, справочниками, выполнять чертежи, схемы, таблицы, решать разного рода задачи, делать вычисления.
Задачи, которые решаются в ходе практических занятий по математике:
1) расширение и закрепление теоретических знаний по математике, полученных в ходе лекционных занятий;
2) формирование у обучающихся практических умений и навыков, необходимых для успешного решения задач по математике;
3) развитие у обучающихся потребности в самообразовании и совершенствовании знаний и умений в процессе изучения математики;
4) формирование творческого отношения и исследовательского подхода в процессе изучения математики;
5) формирование профессионально-значимых качеств будущего специалиста и навыков приложения полученных знаний в профессиональной сфере.
Критерии оценки:
Ответ оценивается отметкой «5», если:
работа выполнена полностью; в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможны некоторые неточности, описки, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка, или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущено не более двух ошибок или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Преподаватель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
3.Методические указания по выполнению практической работы №1: «Теория множеств»
Цель работы:
Используя теоретический материал и образцы решения задач, решить примеры по теме «Теория множеств»
Перечень справочной литературы :
Спирина М.С.Дискретная математика. – М.: «Академия», 2014
Канцедал С.А. Дискретная математика – М.: «ИНФРА-М», 2014
3. Ф.А.Новиков.Дискретная математика для программистов. Питер, 2013
4. Бабичева, И.В. Дискретная математика. Контролирующие материалы к тестированию: Учебное пособие. Лань, 2013. - 160 c.
5. Баврин, И.И. Дискретная математика для педагогических вузов: Учебник и задачник для прикладного бакалавриата. Юрайт, 2015. - 208 c.
Краткие теоретические сведения:
О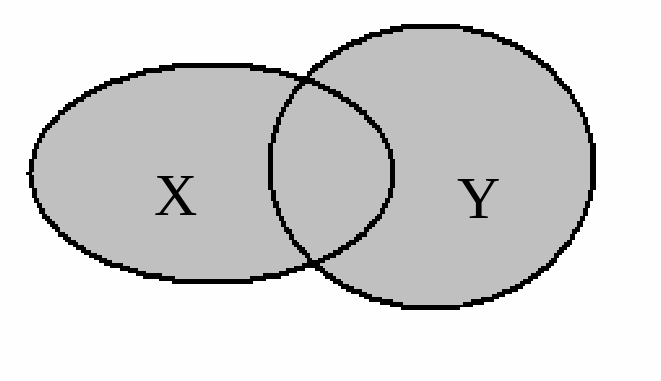
бъединением (суммой) множеств X и Y (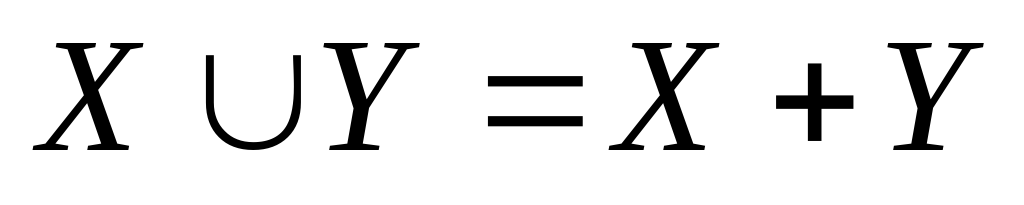 ) называется множество, состоящее из всех этих элементов, которые принадлежат хотя бы одному из множеств X и Y.
) называется множество, состоящее из всех этих элементов, которые принадлежат хотя бы одному из множеств X и Y.
Рис.1. Объединение множеств
Пересечением (произведением) множеств X и Y (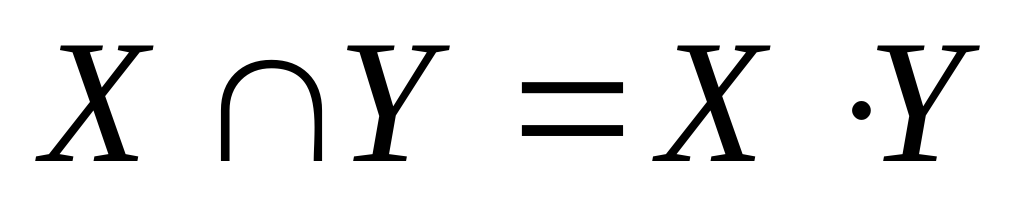 ) называется множество, состоящее элементов, которые принадлежат множествам X и Y.
) называется множество, состоящее элементов, которые принадлежат множествам X и Y.
Р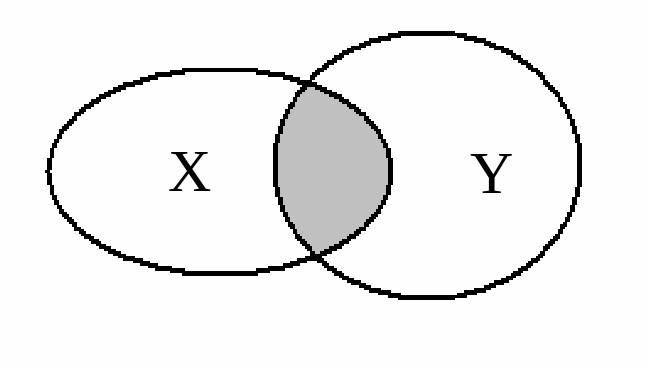
ис.2. Пересечение множеств
Разностью множеств X и Y (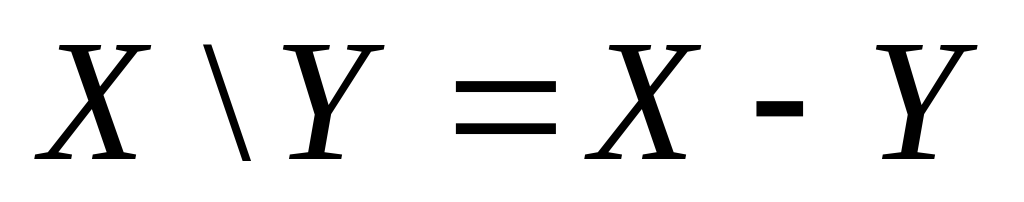 ) называется множество, состоящее из всех тех элементов, которые принадлежат множеству X и не принадлежат множеству Y. Очевидно, что X \ Y Y \ X.
) называется множество, состоящее из всех тех элементов, которые принадлежат множеству X и не принадлежат множеству Y. Очевидно, что X \ Y Y \ X.
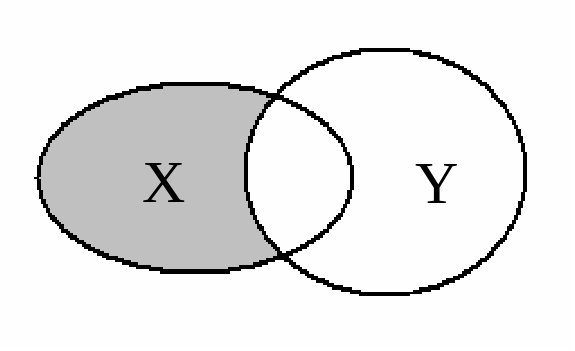 Рис.3. Разность множеств X и Y
Рис.3. Разность множеств X и Y
Симметричной разностью множеств X и Y ( =
=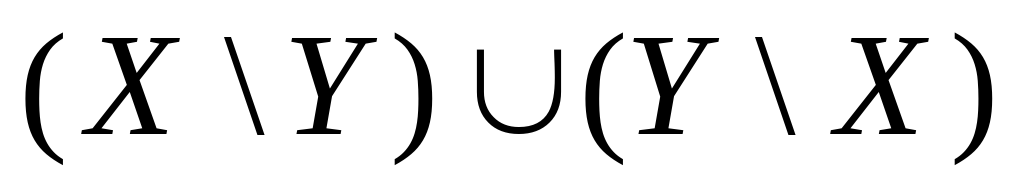 ) называется множество, являющейся объединением разностей X\Y и Y\X.
) называется множество, являющейся объединением разностей X\Y и Y\X.
Пример 1.
X – множество отличников в группе.
Y – множество студентов, живущих в общежитииX
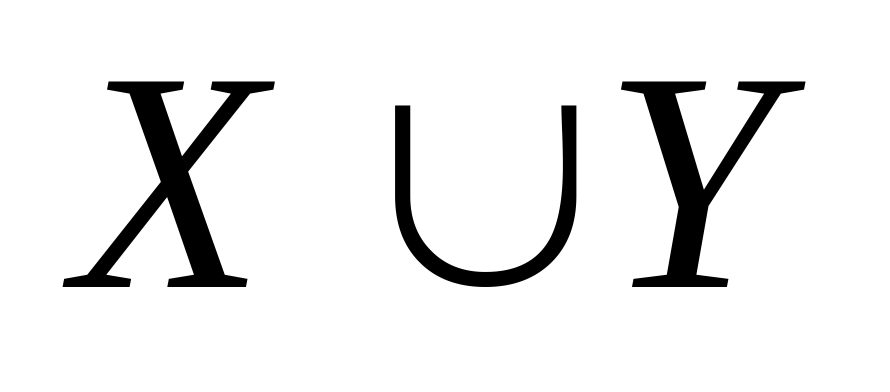 – множество студентов, которые учатся на отлично или живут в общежитии.
– множество студентов, которые учатся на отлично или живут в общежитии.
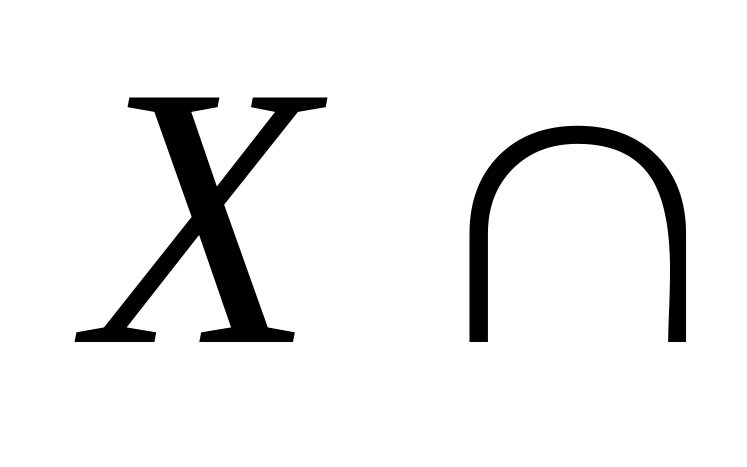 Y – множество отличников, которые живут в общежитии.
Y – множество отличников, которые живут в общежитии.
X\Y – множество отличников, которые не живут в общежитии.
Y\X – множество студентов, живущих в общежитии и не учащихся на отлично.
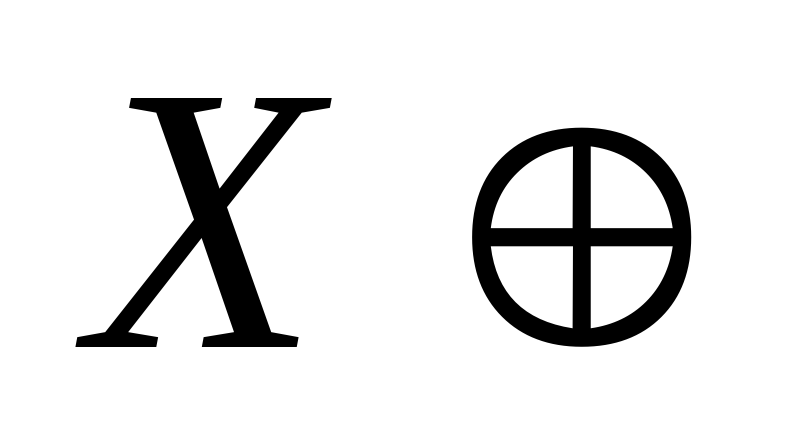 Y – множество отличников, не живущих в общежитии и множество неотличников, живущих в общежитии.
Y – множество отличников, не живущих в общежитии и множество неотличников, живущих в общежитии.
Д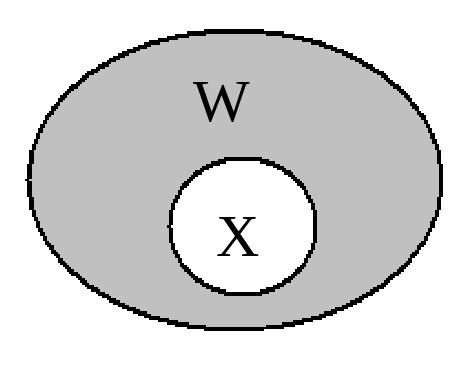 ополнительным к множеству X по отношению к множеству W, если
ополнительным к множеству X по отношению к множеству W, если  , называется множество, состоящее из элементов множества W, не принадлежащих множеству X.
, называется множество, состоящее из элементов множества W, не принадлежащих множеству X.
Рис.4. Дополнительное множество
Универсальным множеством I называется множество, для которого справедливо соотношение 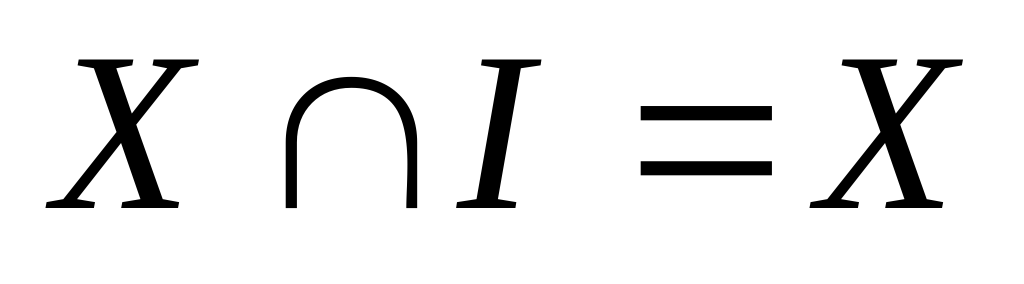 . Множество I содержит все элементы множества X. Следовательно, любое множество X полностью содержится во множестве I, т. е. является его подмножеством
. Множество I содержит все элементы множества X. Следовательно, любое множество X полностью содержится во множестве I, т. е. является его подмножеством 
 . Для предыдущего примера I – это множество студентов.
. Для предыдущего примера I – это множество студентов.
Дополнением множества X (до универсального множества I) называется множество 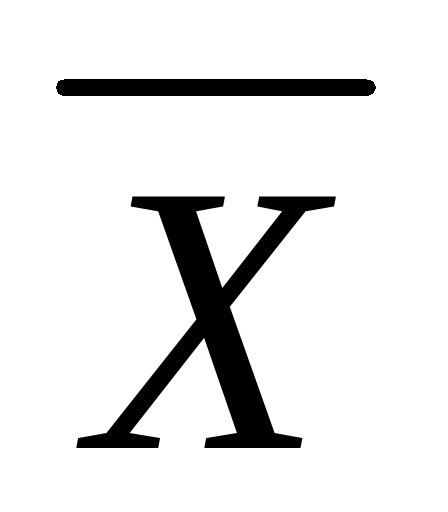 , определяемое из соотношения
, определяемое из соотношения 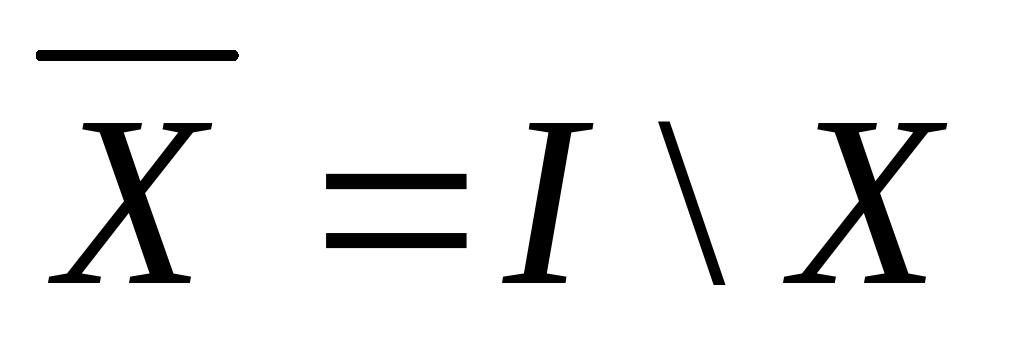 .
.
Очевидно, что 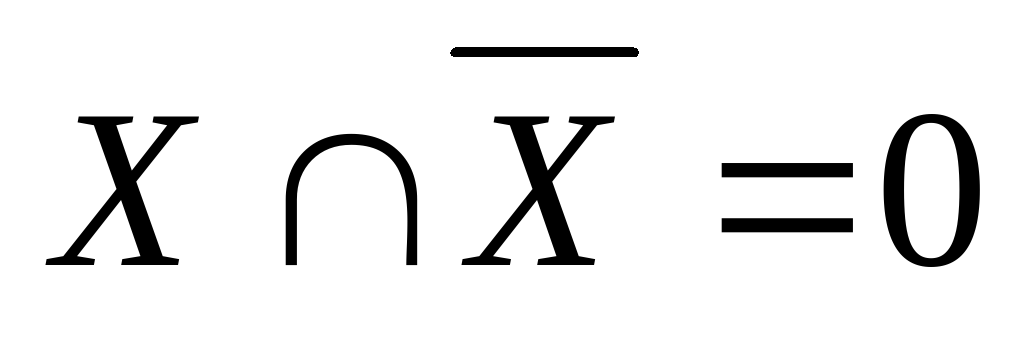 ,
, 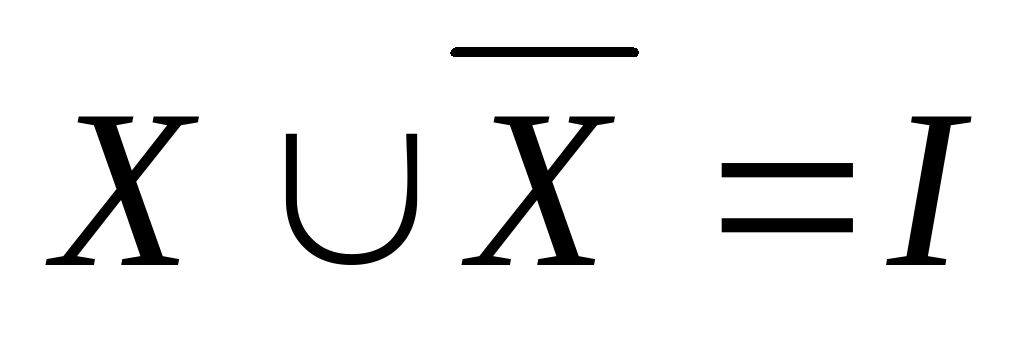 ,
, 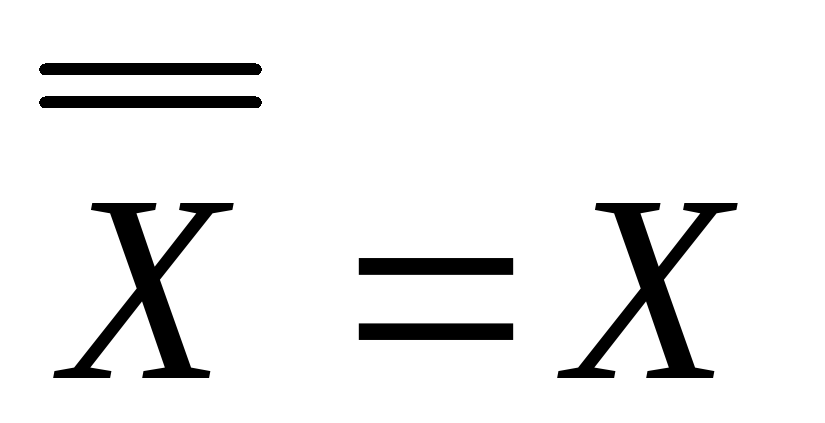
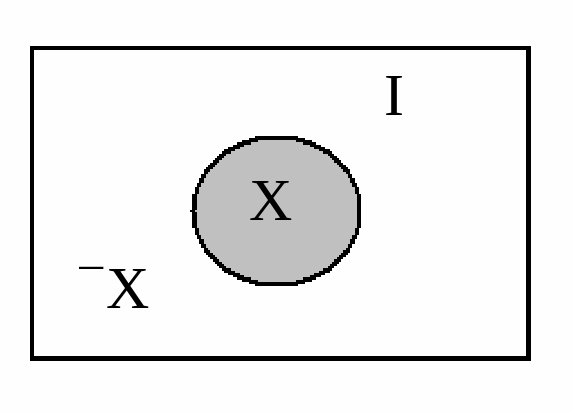
Рис.5. Множество Х и его дополнениеХ
Декартово произведением множеств 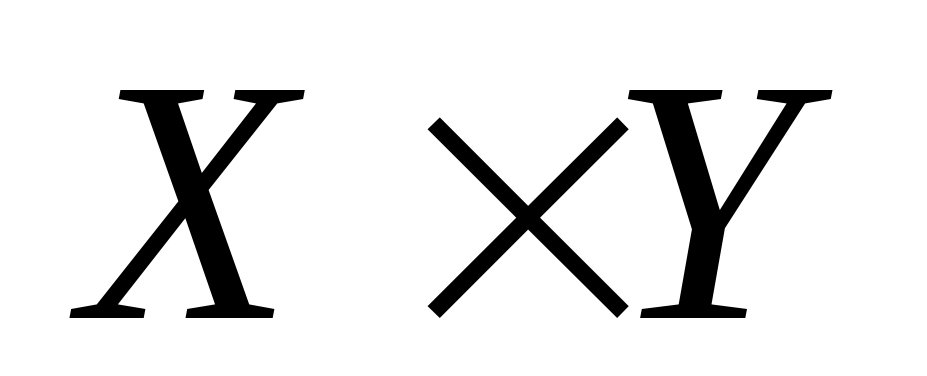 двух множеств X и Y называют множество всех упорядоченных пар (x,y) таких, что
двух множеств X и Y называют множество всех упорядоченных пар (x,y) таких, что 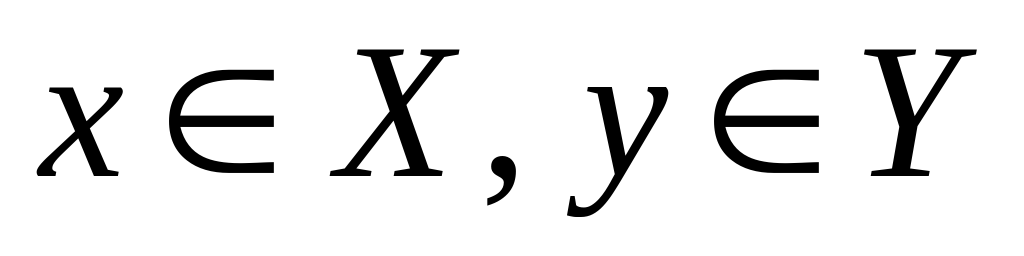 .
.
Пример 2.
Пусть: X = {1,2}, Y = {-1,0,1} .
X Y = (1,-1), (1,0), (1,1), (2,-1), (2,0), (2,1) ,
Y X = (-1,1), (-1,2), (0,1), (0,2), (1,1), (1,2) .
Пример 3.
Пусть X = {x1, x2, x3, x4} и Y = {у1, у2, у3}.
Декартово произведение X Y удобно представить в виде таблицы (матрицы).
|
X \ Y | у1 | у2 | у3 |
| x1 | (x1, у1) | (x1, y2) | (x1, у3) |
| х2 | (х2, у1) | (х2, y2) | (x2, у3) |
| х3 | (х3, у1) | (х3, y2) | (x3, у3) |
| х4 | (х4, у1) | (х4, y2) | (х4, у3) |
На множестве X задано бинарное отношение R, если задано подмножество декартова произведения X X (т. е. R X X).
Пример 4.
Пусть X = {1, 2, 3, 4}. Зададим на X следующие отношения:
Т = {(х, у) | х, у Х; х = у} – отношение равенства;
Р = {(х, у) | х, у Х; х = у - 1} – отношение предшествования;
Q = {(х, у) | х, у Х; х делится на у} – отношение делимости.
Все эти отношения заданы с помощью характеристического свойства. Перечислим элементы этих отношений для заданного множества X = {1,2,3,4}:
Т = {(1,1), (2,2), (3,3), (4,4)};
P = {(1,2), (2,3), (3,4) };
Q = {(4,4), (4,2), (4,1), (3,3), (3,1), (2,2), (2,1), (1,1)}.
Отношение R на множестве X называется рефлексивным, если для всех х X выполняется условие (х, х) R. Отношение R на множестве Х называется нерефлексивным, если условие (х, х) R не выполняется хотя бы при одном х X .
Отношение R на множестве X называется симметричным, если из условия (х, у) R следует (у, х) R. Отношение R на множестве X называется несимметричным, если для любых х, у X из условия (х, y) R следует (у, х) R.
Отношение R на множестве X называется транзитивным, если для любых х, у, z R из одновременного выполнения условий (x, y) R и (у, z) R следует (х, z) R .
Пример 5.
Рассмотрим следующие отношения на множестве X = {1,2,3,4,5,6,7}:
G = {(x, y) | х, у Х; х у};
L = {(х, у) | х, у Х; х у};
M = {(x, y) | х, у X; (х - у) делится на 3};
К = {(х, y) | х, у Х; х2 + у2 20}.
Исследуем, какими свойствами они обладают.
Среди приведенных в примере отношений рефлексивными являются отношение L (т. к. х х справедливо при всех х X) и отношение М (т. к. х - х = 0 делится на 3, поэтому пара (х, х) принадлежит отношению М при всех х X).
Симметричными являются отношения М (если х - у делится на 3, то и у - х делится на 3) и К (если х2 + у2 20, то и у2 + х2 20).
Транзитивными являются отношения G, L, М.
Порядок выполнения работы:
Используя теоретические сведения выполнить предложенное преподавателем задание
Примеры по теме:
1. Для множеств S = {4,5,6,7,8} и T = { 4, 6, 8 }
Определить S U T, S T, S \ T, S x T, T x S.
2. В ученической производственной бригаде 86 старшеклассников. 8 из них не умеют работать ни на тракторе, ни на комбайне. 54 ученика хорошо овладели трактором, 62 — комбайном. Сколько человек из этой бригады могут работать и на тракторе, и на комбайне?
3. Обведите кружком номер правильного ответа. Областью определения бинарного отношения R называется множество
а) {(х, у)| (х, у) R};
б) {х| (х, у) R};
в) {у| (х, у) R}.
4. Какой особенностью обладает матрица рефлексивного отношения? А матрица симметричного отношения?
Содержание отчета
Отчет должен содержать:
4.1 Название работы
4.2 Цель работы
4.3 Задание
4.4 Формулы расчета
4.5 Результат
4.Методические указания по проведению практической работы №2:
«Графы»
Цель работы:
Используя теоретический материал и образцы решения задач, решить примеры по теме «Графы».
Перечень справочной литературы :
Спирина М.С.Дискретная математика. – М.: «Академия», 2014
Канцедал С.А. Дискретная математика – М.: «ИНФРА-М», 2014
3. Ф.А.Новиков.Дискретная математика для программистов. Питер, 2013
4. Бабичева, И.В. Дискретная математика. Контролирующие материалы к тестированию: Учебное пособие. Лань, 2013. - 160 c.
5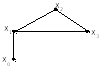
. Баврин, И.И. Дискретная математика для педагогических вузов: Учебник и задачник для прикладного бакалавриата. Юрайт, 2015. - 208 c.
Краткие теоретические сведения:
Граф G задается множеством вершин (точек) Х = {х1, ..., хn} и множеством ребер (линий) А = {а1, .., аn}, соединяющих между собой все или часть этих вершин. Таким образом, граф G полностью определяется заданием двух множеств (Х, А).
Ребра графа – линии, соединяющие вершины, указывают на соответствие между вершинами в графе.
Запись g = (xi, xj) говорит, что ребро g инцидентно вершинам хi и xj, а вершины хi, xj инцидентны ребру g. Две вершины хi, xj называются смежными, если они определяют ребро графа. Два ребра графа называются смежными, если их концы имеют общую вершину.
Степенью m(х) графа G(X) в вершине х называется число ребер, инцидентных вершине х.
М

аршрутом в произвольном графе называется чередующаяся последовательность вершин и ребер, начинающаяся и заканчивающаяся вершиной.
Цепь – последовательность ребер S = (g1, g2, ..., gn), в которой у каждого ребра gk одна из вершин является вершиной ребра gk-1, а другая - вершиной ребра gk+1. При этом одно и то же ребро или вершина может встречаться несколько раз. Пример цепи для графа (рис. 7):
S
= (g0, gl, g2, g3, g4, g5, g2, gб) = ((x0, х1), (х1, х2), (х2, х3), (х3, х1), (х1, х4), (х4, х3), (х3, х2), (х2, х5)).
Рис. 6. Пример цепи
П одграфом GA(A) графа G(X), где А X, называется граф, вершинами которого являются элементы множества А X, а ребрами – все ребра из G, концевые вершины которых лежат в А (рис. 8).
одграфом GA(A) графа G(X), где А X, называется граф, вершинами которого являются элементы множества А X, а ребрами – все ребра из G, концевые вершины которых лежат в А (рис. 8).
Рис. 7. Граф G(X)
Таким образом, подграф содержит часть вершин вместе с ребрами, соединяющими эти вершины. Иначе, GA(A) – подграф графа G(X), если А X и GA(x) = G(x)А х Х.
Рис. 8. Подграф GA(A) графа G(X)
Компонентой связности неориентированного графа G(X) называется подграф НА(А) графа G(X) с множеством вершин А X и множеством ребер в G(X), инцидентных только вершинам из А, причем ни одна вершина xi А не смежна с вершинами из множества Х \ А (рис. 9).
Рис. 9. Граф с двумя компонентами связности
Деревом называется конечный связный неориентированный граф, состоящий, по крайней мере, из двух вершин и не содержащий циклов. Такой граф не имеет петель и кратных ребер.
Рис. 10. Дерево
Цикломатическое число. Пусть G(X) – неориентированный граф, имеющий n вершин, m ребер и k компонент связности. Цикломатическим числом графа G называется число µ(G) = m - n + k.
Это число имеет интересный физический смысл: оно равно наибольшему числу базисных (независимых) циклов в графе.
Остовом T графа G называется называется подграф графа в виде дерева, содержащий все его вершины. Остов определяет каркас графа.
Кодеревом T* остова Т называется подграф графа G, содержащий все вершины и только те ребра, которые не входят в остов Т. Ребра остова называют ветвями, а ребра кодерева - хордами.
Обход графа - это маршрут, содержащий все ребра или вершины графа и обладающий определенными свойствами. Наиболее известными обходами графа являются эйлеровы и гамильтоновы цепи и циклы.
Теорема (Эйлера). Конечный связный неориентированный мультиграф является эйлеровым графом тогда и только тогда, когда в нем отсутствуют вершины нечетной степени.
Гамильтоновой цепью в неориентированном графе называется цепь, проходящая через каждую его вершину один и только один раз.
Гамильтоновым циклом в неориентированном графе называется цикл, проходящий через каждую вершину один и только один раз за исключением начальной вершины, которая совпадает с конечной.
Гамильтоновым путем в ориентированном графе называется путь S = (х1, ..., хn), проходящий через все вершины графа, притом только по одному разу.
Гамильтоновым контуром называется контур М=(х0, х1, ..., хn, х0) в ориентированном графе G(X), если он проходит через все вершины графа по одному разу.
Граф отношения R X X строится следующим образом. На плоскости в произвольном порядке изображаются точки - элементы множества X. Пара точек х и у соединяется дугой (линией со стрелкой) тогда и только тогда, когда пара (х, у) принадлежит отношению R.
Матрица отношения R X X – это квадратная таблица, каждая строка и столбец которой соответствует некоторому элементу множества X. На пересечении строки х и столбца у ставится 1, если пара (х, у) R; все остальные элементы матрицы заполняются нулями. Элементы матрицы нумеруются двумя индексами, первый равен номеру строки, второй – номеру столбца.
Пусть X = {х1, х2, …, хn}. Тогда матрица отношения
R X X имеет n строк и n столбцов, а ее элемент rij определяется по правилу:
 1, если (xi, yj) R, где i = l, 2, ..., n; j = l, 2, ..., n.
1, если (xi, yj) R, где i = l, 2, ..., n; j = l, 2, ..., n.
r = 0, если (xi, yj) R.
ij =
Рис.11. Граф отношения Q (а) и матрица отношения Q (б)
Е
сли в графе G(X) через аij обозначить число дуг, идущих из xi в xj, то матрица A = || аij || (i = 1, ..., n; j=1, ..., n; где n – число вершин графа) называется матрицей смежности вершин графа. Наличие нулевого элемента на главной диагонали означает отсутствие петли в соответствующей вершине.
Рис. 12. Пример графа для определения матрицы смежности A

Д
rij =
ля неориентированного графа матрица R = || r
ij || размером n х m, где:
1, если хi (i = 1, ..., n) инцидентна gj (j = 1, ..., m), 0, в противном случае называется матрицей инциденций для ребер графа.
Функция f(x1, х2, ..., xn), принимающая логическое значение (1 или 0) и зависящая от логических переменных, называется логической функцией.
Область определения логической функции – совокупность всевозможных n-мерных наборов из нулей и единиц, а для её задания достаточно указать, какие значения функции соответствуют каждому из наборов (табл.2.)
Порядок выполнения работы:
Используя теоретические сведения выполнить предложенное преподавателем задание
Примеры по теме:
Задан граф G=(X, U)
1) Записать матрицу смежности.
2) Пронумеровать ребра и построить матрицу инциденций.
g1 →(x1, x2) g2 →(x2, x3) g3 →(x3, x4) g4 →(x1, x5)
g5 →(x4, x6) g6 →(x3, x6) g7 →(x2, x5) g8 →(x3, x5)
g9 →(x2, x6) g10 →(x5, x6)
3)Найти степени всех вершин графа m(xi), (xi·X) и вычислить сумму m(xi).
4) Построить простую цепь максимальной длины, связывающую вершины х1 и х5.
5) Построить эйлеров цикл (начиная с x1, все ребра проходить один раз и вернуться в x1).
6) Удалив из графа ребро g4 , соединяющие вершины{х1,х3}, построить эйлерову цепь.
7) Привести пример гамильтонова цикла, начинающегося с вершины х1 Найти цикломатическое число и привести пример дерева, являющегося составным подграфом.
Содержание отчета
Отчет должен содержать:
4.1 Название работы
4.2 Цель работы
4.3 Задание
4.4 Формулы расчета
4.5 Результат
5.Методические указания по проведению практической работы №3:
«Матлогика»
Цель работы:
Используя теоретический материал и образцы решения задач, решить примеры по теме «Матлогика»
Перечень справочной литературы :
1. Спирина М.С.Дискретная математика. – М.: «Академия», 2014
2. Канцедал С.А. Дискретная математика – М.: «ИНФРА-М», 2014
3. Ф.А.Новиков.Дискретная математика для программистов. Питер, 2013 4. Бабичева, И.В. Дискретная математика. Контролирующие материалы к тестированию: Учебное пособие. Лань, 2013. - 160 c.
5. Баврин, И.И. Дискретная математика для педагогических вузов: Учебник и задачник для прикладного бакалавриата. Юрайт, 2015. - 208 c.
Краткие теоретические сведения:
Если X, Y, Z – логические переменные то, применяя к ним операции конъюнкции, дизъюнкции, импликации, эквивалентности и отрицания, можно получить формулы алгебры логики.
При задании конкретных значений переменных формула принимает определенное значение. Таким образом, каждая формула определяет некоторую логическую функцию, переменными которой являются переменные высказывания.
Переменные и функции принимают только два значения (1 или 0), поэтому логические функции можно описать конечной таблицей, которую называют таблицей истинности.
Рассмотренные выше логические выражения определяют основные функции двух переменных f(x, y) формулами: x y, x y, х у, х у,x. Ниже приведена их таблица истинности (табл. 1).
Таблица 1. Таблица истинности основных функций
| x | y | x y | x y | х у | x y | x |
| 0
| 0 | 0 | 0 | 1 | 1 | 1 |
| 0
| 1 | 0 | 1 | 1 | 0 | 1 |
| 1
| 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 |
Функция f(x1, х2, ..., xn), принимающая логическое значение (1 или 0) и зависящая от логических переменных, называется логической функцией.
Область определения логической функции – совокупность всевозможных n-мерных наборов из нулей и единиц, а для её задания достаточно указать, какие значения функции соответствуют каждому из наборов (табл.2.)
Наборы в таблице будем располагать в порядке возрастания их номера N. Такой порядок расположения наборов называется стандартным или естественным.
При таком порядке каждому набору α = (α1, …, αn), где αi есть 0 или 1, ставится в соответствие целое число
N = α12n-1+ … + αn-121+ αn.
Наборам (0, 0, ...,0, 0), (0, 0, ..., 0, 1), ..., (1, 1, ..., 1, 1) соответствуют числа N = 0, 1,..., 2n-1. Количество входных наборов для функции n переменных равно k = 2n.
Таблица 2. Задание логической функции
| N | х1 | х2 | … | хn-1 | хn | f(x1, x2,..., xn-1, хn) |
| 0 | 0 | 0 | … | 0 | 0 | f(0, 0, ..., 0, 0) |
| 1 | 0 | 0 | … | 0 | 1 | f(0, 0, ..., 0, l) |
| … | … | … | … | … | … | ……………… |
| 2n-2 | 1 | 1 | … | 1 | 0 | f(l, 1, …, 1, 0) |
| 2n-1 | 1 | 1 | … | 1 | 1 | f(l, 1, …, 1, 1) |
Все множество наборов переменных по значениям функции на них можно разбить на 2 подмножества:
[1] – единичное множество наборов, на которых f = 1;
[0] – нулевое множество наборов, на которых f = 0.
Теперь определим количество различных функций n переменных. Каждая функция задается набором своих k значений, которому также можно поставить в соответствие k-разрядное двоичное число.
Располагая функции в таблице в порядке возрастания соответствующих им чисел, мы получим все возможные различные функции. Количество таких функций будет равно .
Совершенная дизъюнктивная нормальная формой (СДНФ).
Эта формула называется совершенной дизъюнктивной нормальной формой (СДНФ) функции f(x1, х2,..., xn).
Следствие. Для произвольной логической функции существует взаимнооднозначное соответствие между ее СДНФ и таблицей истинности:
а) СДНФ содержит ровно столько элементарных конъюнкций, сколько единичных наборов у функции;
б) каждому единичному набору σ = (σ1, …, σn) соответствует элементарная конъюнкция всех переменных функции, в которой для σi = 0 переменная хi берется с отрицанием и для σi = 1 – без отрицания.
Совершенная конъюнктивная нормальная формой (СКНФ).
Эта форма называется совершенной конъюнктивной нормальной формой (СКНФ).
Следствие. Для произвольной логической функции также существует взаимнооднозначное соответствие между ее СКНФ и таблицей истинности:
а) СКНФ содержит ровно столько элементарных дизъюнкций, сколько нулевых наборов у функции;
б) каждому нулевому набору σ = (σ1, …, σn) соответствует элементарная дизъюнкция всех переменных функции, в которой для σi = 1 переменная хi берется с отрицанием и для σi = 0 – без отрицания.
Минимизация ДНФ
Метод получения сокращённой ДНФ функции f(x1, ..., xn) из ее совершенной ДНФ состоит в применении следующих эквивалентных преобразований:
а) операции полного склеивания, которая состоит в замене выражения А х Ах на А, так как
А х Ах А (х х) A • 1 A;
б) операции неполного склеивания, которая состоит в замене А х Ах на А х Ах А, так как
А х Ах А А (х х) А А•1 A = A;
в) операции поглощения, которая состоит в замене АВ А на А, так как
АВ А А (В 1) А.
Здесь А и В – произвольные элементарные конъюнкции.
Теорема: Сокращённую ДНФ функции f(x1, ..., xn) можно получить из ее совершенной ДНФ, применяя все возможные операции неполного склеивания, а затем операции поглощения.
Порядок выполнения работы:
Используя теоретические сведения выполнить предложенное преподавателем задание
Примеры по теме:
Используя теоретические сведения выполнить предложенное преподавателем задание
1. По заданной таблице истинности построить совершенную дизъюнктивную нормальную форму.
| x1 | X2 | x3 | f(x1,x2,x3) |
| x1 | x2 | x3 | f(x1,x2,x3) |
| 0 | 0 | 0 |
|
| 1 | 0 | 0 |
|
| 0 | 0 | 1 |
|
| 1 | 0 | 1 |
|
| 0 | 1 | 0 |
|
| 1 | 1 | 0 |
|
| 0 | 1 | 1 |
|
| 1 | 1 | 1 |
|
2. По заданной таблице истинности построить совершенную конъюнктивную нормальную форму.
3. Определить сложность форм и выполнить упрощение их. Объясните полученные результаты
5. Каждый из четырех гномов - Дварин, Ринин, Ферин и Торин - либо всегда говорит правду, либо всегда врет. Однажды они начали спорить, кто из них врет, а кто нет. Вот часть их разговора: Дварин - Ририну: «Ты врун», Ферин – Дварину: «Это ты врун», Торин – Ферину: «Дварин и Ринин – оба вруны. И ты тоже!»
Кто из гномов говорит правду, а кто врет, если известно, что Ринин всегда говорит
правду? В ответе укажите сначала первые буквы имен гномов? В ответе укажите сначала первые буквы имен гномов, которые говорят правду, в алфавитном порядке, а затем тех, которые лгут, тоже в алфавитном порядке.
6. На столе лежат в ряд четыре предмета: ручка, карандаш, фломастер и маркер. Они окрашены в разные цвета: оранжевый, синий, желтый, зеленый. Известно, что фломастер лежит правее и ручки, и карандаша; синий предмет лежит между оранжевым и зеленым; слева от желтого предмета лежит карандаш; маркер и карандаш лежит не с краю; синий и оранжевый предметы лежат не рядом. Определите, в каком порядке лежат предметы и какого они цвета.
Содержание отчета
Отчет должен содержать:
4.1 Название работы
4.2 Цель работы
4.3 Задание
4.4 Формулы расчета
4.5 Результат
6.Методические указания по проведению практической работы №4: «Логика предикатов».
Цель работы:
Используя теоретический материал и образцы решения задач, решить примеры по теме «Логика предикатов»
Перечень справочной литературы :
1. Спирина М.С.Дискретная математика. – М.: «Академия», 2014
2. Канцедал С.А. Дискретная математика – М.: «ИНФРА-М», 2014
3. Ф.А.Новиков.Дискретная математика для программистов. Питер, 2013 4. Бабичева, И.В. Дискретная математика. Контролирующие материалы к тестированию: Учебное пособие. Лань, 2013. - 160 c.
5. Баврин, И.И. Дискретная математика для педагогических вузов: Учебник и задачник для прикладного бакалавриата. Юрайт, 2015. - 208 c.
Краткие теоретические сведения:
Неформально говоря, предикат – это высказывание, в которое можно подставлять аргументы. Если аргумент один – то предикат выражает свойство аргумента, если больше – то отношение между аргументами.
Пример предикатов. Возьмём высказывания: ``Сократ - человек'', ``Платон - человек''. Оба эти высказывания выражают свойство ``быть человеком''. Таким образом, мы можем рассматривать предикат ``быть человеком'' и говорить, что он выполняется для Сократа и Платона.
Пример рассуждения, не выразимого в логике высказываний. Все люди смертны. Сократ - человек. Следовательно, Сократ смертен.
Это рассуждение на языке логики высказываний можно записать тремя отдельными высказываниями. Однако никакой связи между ними установить не удастся. На языке логики предикатов эти предложения можно выразить с помощью двух предикатов: ``быть человеком'' и быть смертным''. Первое предложение устанавливает связь между этими предикатами.
Перейдём теперь к формальному изложению логики предикатов.
Язык логики предикатов
| Предикатная сигнатура – это множество символов двух типов – объектные константы и предикатные константы – с неотрицательным целым числом, называемым арностью, назначенным каждой предикатной константе. Предикатную константу мы будем называть пропозициональной, если её арность равна 0. Пропозициональные константы являются аналогом атомов в логике высказываний. Предикатная константа унарна, если её арность равна 1, и бинарна, если её арность равна 2. Например, мы можем определить предикатную сигнатуру{ a, P, Q } |
|
объявляя a объектной константой, P – унарной предикатной константой, и Q – бинарной предикатной константой.
Определение. Квантором всеобщности (обозначение - ∀) высказывания А(х), x∈X, называется логическая операция, имеющая значение "истина", если высказывание А(х) истинно для любого элемента x∈ X, и значение "ложь" в противоположном случае (т.е. в случае, когда хотя бы для одного x∈X высказывание А(х) ложно).
Примеры: высказывание ("∀х ∈ [-2,4], x2 -2) - истинно, высказывание ("∀х ∈ [-2,4], x2 16) - ложно, высказывание ("∀х ∈ N, x2 0) - истинно, высказывание ("∀х ∈ R, x2 0) - ложно.
Определение. Квантором существования (обозначение - ∃) высказывания А(х), x ∈ X, называется логическая операция, имеющая значение "истина", если высказывание А(х)истинно хотя бы для одного элемента x ∈ X, и значение "ложь" в противоположном случае (т.е. в случае, когда высказывание А(х) ложно для всех x ∈ X).
Формула ∃х∈Х, А(х) читается как "существует ( найдётся) (хотя бы один) элемент х, принадлежащий Х, для которого справедливо А(х)". Формальное определение квантора существования:
Примеры: высказывание (∃ х ∈ [-2,4], x2 20) - ложно, высказывание (∃ х ∈ [-2,4], x2 10) - истинно, высказывание (∃ х ∈ N, x2 = 0) - ложно, высказывание (∃ х ∈ R, x2 = 0) - истинно.
Порядок выполнения работы:
Используя теоретические сведения выполнить предложенное преподавателем задание
Примеры по теме:
1. Проверить истинность высказывания:
а) Чтобы завтра пойти на занятия, я должен встать рано. Если я сегодня пойду в кино, то лягу спать поздно. Если я лягу спать поздно, то встану поздно. Следовательно, либо я не пойду в кино, либо не пойду на занятия.
б) Я пойду либо в кино, либо в бассейн. Если я пойду в кино, то получу эстетическое удовольствие. Если я пойду в бассейн, то получу физическое удовольствие. Следовательно, если я получу физическое удовольствие, то не получу эстетического удовольствия.
2. На вопрос: «Кто из трех студентов изучал дискретную математику?» получен верный ответ: «Если изучал первый, то изучал и третий, но неверно, что если изучал второй, то изучал и третий». Кто изучал дискретную математику?
3. Определите, кто из четырех студентов сдал экзамен, если известно:
если первый сдал, то и второй сдал;
если второй сдал, то третий сдал или первый не сдал;
если четвертый не сдал, то первый сдал, а третий не сдал;
если четвертый сдал, то и первый сдал.
4. Вычислите значение функции при заданных значениях аргументов
5. Определить тождественно истинность формулы 
6. Определить тождественно ложность формулы
Содержание отчета
Отчет должен содержать:
4.1 Название работы
4.2 Цель работы
4.3 Задание
4.4 Формулы расчета
4.5 Результат
7.Методические указания по проведению практической работы №5:
«Конечные автоматы»
Цель работы:
Используя теоретический материал и образцы решения задач, решить примеры по теме «Конечные автоматы»
Перечень справочной литературы :
1. Спирина М.С.Дискретная математика. – М.: «Академия», 2014
2. Канцедал С.А. Дискретная математика – М.: «ИНФРА-М», 2014
3. Ф.А.Новиков.Дискретная математика для программистов. Питер, 2013 4. Бабичева, И.В. Дискретная математика. Контролирующие материалы к тестированию: Учебное пособие. Лань, 2013. - 160 c.
5. Баврин, И.И. Дискретная математика для педагогических вузов: Учебник и задачник для прикладного бакалавриата. Юрайт, 2015. - 208 c.
Краткие теоретические сведения:
Конечный автомат- это модель вычислений, основанная на гипотетической машине состояний. В один момент времени только одно состояние может быть активным. Следовательно, для выполнения каких-либо действий машина должна менять свое состояние.
Конечные автоматы обычно используются для организации и представления потока выполнения чего-либо. Это особенно полезно при реализации ИИ в играх. Например, для написания «мозга» врага: каждое состояние представляет собой какое-то действие.
Конечный автомат можно представить в виде графа, вершины которого являются состояниями, а ребра — переходы между ними. Каждое ребро имеет метку, информирующую о том, когда должен произойти переход. Например, на изображении выше видно, что автомат сменит состояние «wander» на состояние «attack» при условии, что игрок находится рядом.
Реализация конечного автомата начинается с выявления его состояний и переходов между ними. Представьте себе конечный автомат, описывающий действия муравья, несущего листья в муравейник:
Описание состояний интеллекта муравья
Отправной точкой является состояние «find leaf», которое остается активным до тех пор, пока муравей не найдет лист. Когда это произойдет, то состояние сменится на «go home». Это же состояние останется активным, пока наш муравей не доберется до муравейника. После этого состояние вновь меняется на «find leaf».
Если состояние «find leaf» активно, но курсор мыши находится рядом с муравьем, то состояние меняется на «run away». Как только муравей будет в достаточно безопасном расстоянии от курсора мыши, состояние вновь сменится на «find leaf».
Обратите внимание на то, что при направлении домой или из дома муравей не будет бояться курсора мыши. Почему? А потому что нет соответствующего перехода.
Описание состояний интеллекта муравья. Обратите внимание на отсутствие перехода между «run away» и «go home»
Конечный автомат можно реализовать при помощи одного класса. Назовем его FSM. Идея состоит в том, чтобы реализовать каждое состояние как метод или функцию. Также будем использовать свойство activeState для определения активного состояния.
Порядок выполнения работы:
Используя теоретические сведения выполнить предложенное преподавателем задание
Примеры по теме:
1. Даны x, y. Составить программу вычисления значения выражения:
2. Составить программу для решения следующей задачи:
а)Дана длина ребра куба. Найти объем куба и площадь его боковой поверхности.
б)Известна длина окружности. Найти площадь круга, ограниченного этой окружностью.
3. Какую функцию вычисляет машина Т со следующей программой:
q10 → q20R,
q11 → q01,
q20 → q01,
q21 → q21R ?
4. Построить машину Тьюринга (представить программу в виде таблицы и в форме диаграммы) для решения следующих задач:
Прибавить 1 к целому неотрицательному числу(вычислить функцию F(x) = x + 1).
Рассмотреть задачу для машины Тьюринга с алфавитами
A = {0, 1, e} (операции выполняются в двоичной системе);
A = {1, e} (строка «…e1e…» соответствует x = 0, в записи любого другого целого числа x 0 количество единиц равно x + 1).
Вычесть 1 из целого неотрицательного числа(вычислить функцию F(x) = x – 1). Операции выполняются по следующему правилу:
.
Рассмотреть задачу для машины Тьюринга с алфавитами
A = {0, 1, e} (операции выполняются в двоичной системе);
A = {1, e} (строка «…e1e…» соответствует записи x = 0 на ленте, в записи любого другого целого числа x 0 количество единиц равно x + 1).
Прибавить 3 к целому неотрицательному числу(вычислить функцию F(x) = x + 3).
машина Тьюринга строится для вычисления указанной функции;
Содержание отчета
Отчет должен содержать:
4.1 Название работы
4.2 Цель работы
4.3 Задание
4.4 Формулы расчета
4.5 Результат









 Рис.3. Разность множеств X и Y
Рис.3. Разность множеств X и Y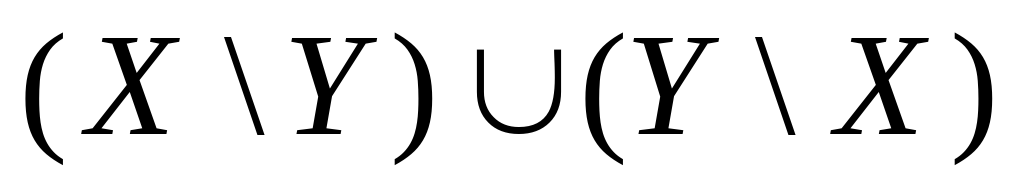 ) называется множество, являющейся объединением разностей X\Y и Y\X.
) называется множество, являющейся объединением разностей X\Y и Y\X. ополнительным к множеству X по отношению к множеству W, если
ополнительным к множеству X по отношению к множеству W, если