Муниципальное автономное общеобразовательное учреждение «Лицей №14 имени Заслуженного учителя Российской Федерации А.М. Кузьмина»
Основы неевклидовых геометрий
Автор проекта:
Ермаков Александр Павлович 10К
_____________
Научный руководитель:
Сухненко Ирина Александровна
_____________
Тамбов 2022
Оглавление.
Введение 3
Глава I. Геометрия Лобачевского 9
Введение 9
§1 Введение в геометрию Лобачевского. Аксиоматика 9
§2 Модели геометрии Лобачевского 10
Глава II. Сферическая геометрия 13
§1 Введение в сферическую геометрию. Аксиоматика. 13
§2 Сферический треугольник. 15
§3 Сферическая система координат. 16
Примечание: 16
Глава III. Практическое применение неевклидовых геометрий. 17
§1 Применение сферической геометрии 17
§2 Применение геометрии Лобачевского 20
§3 Неевклидовы геометрические тела 21
1. Тор 21
2. Лента Мёбиуса 23
Заключение: 25
Список используемых источников: 25
Введение
Геометрия — наука, изучающая пространственные структуры и их отношения, и обобщения, возможно самый изученный раздел математики.
В древности её основания считались наиболее прочными.
Но, когда математики 17 – 18 вв. внимательно изучили эти основания, они задумались о истинности и единственности евклидовой геометрии.
В 1799 году К.Ф. Гаусс задаётся вопросами: «Правдива ли евклидова геометрия? Верно ли она описывает пространство, в котором мы живём?» с первого взгляда может показаться что эта геометрия очень правдоподобна. Но Гауссу было недостаточно одной правдоподобности: «Я всё больше и больше склоняюсь к тому, что истинность нашей геометрии не может быть доказана, возможно в другой жизни у нас был бы другой взгляд на природу пространства, который сейчас нам недоступен. Но до тех пор мы должны ставить геометрию в один ранг не с арифметикой, которая существует чисто априори, а скорее с механикой».
Чтобы понять, как Гаусс мог засомневаться в истинности евклидовой геометрии нужно разобраться с тем, что же значит верить в то, что евклидова геометрия – чистая правда? Как это можно доказать?
Для начала нужно сделать несколько допущений – 5 основных постулатов геометрии (см. приложение 1), без которых мы просто не можем обойтись. Затем необходимо перейти от них к остальным представлениям о физическом пространстве. В таком случае эти представления будут, несомненно, верны, потому что они логически следуют из наших допущений (которые мы принимаем как верные).
 Примечание 1:
Примечание 1:
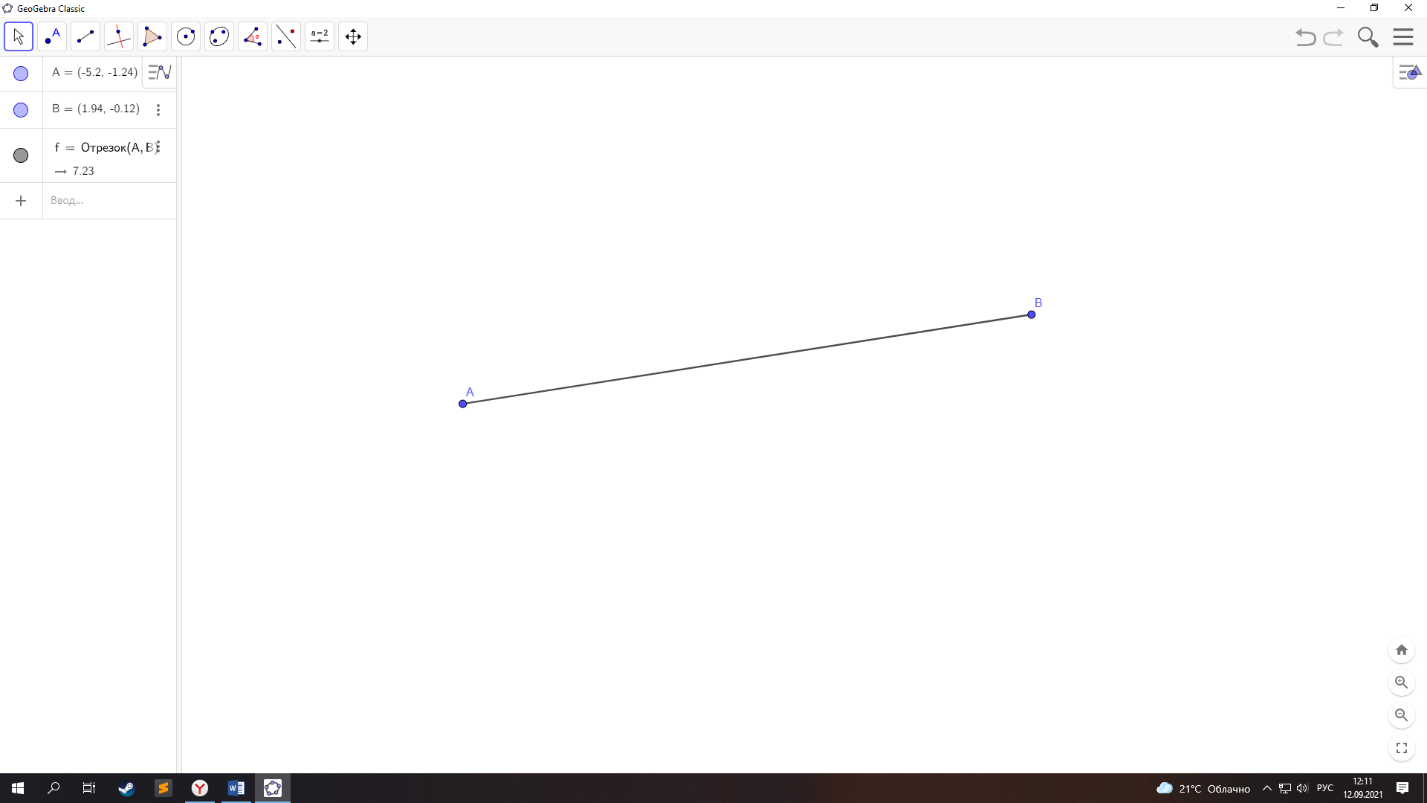
1.1. Первый постулат геометрии: «от всякой точки до всякой точки можно провести прямую» (см. рис. 1.1)
рис. 1.1
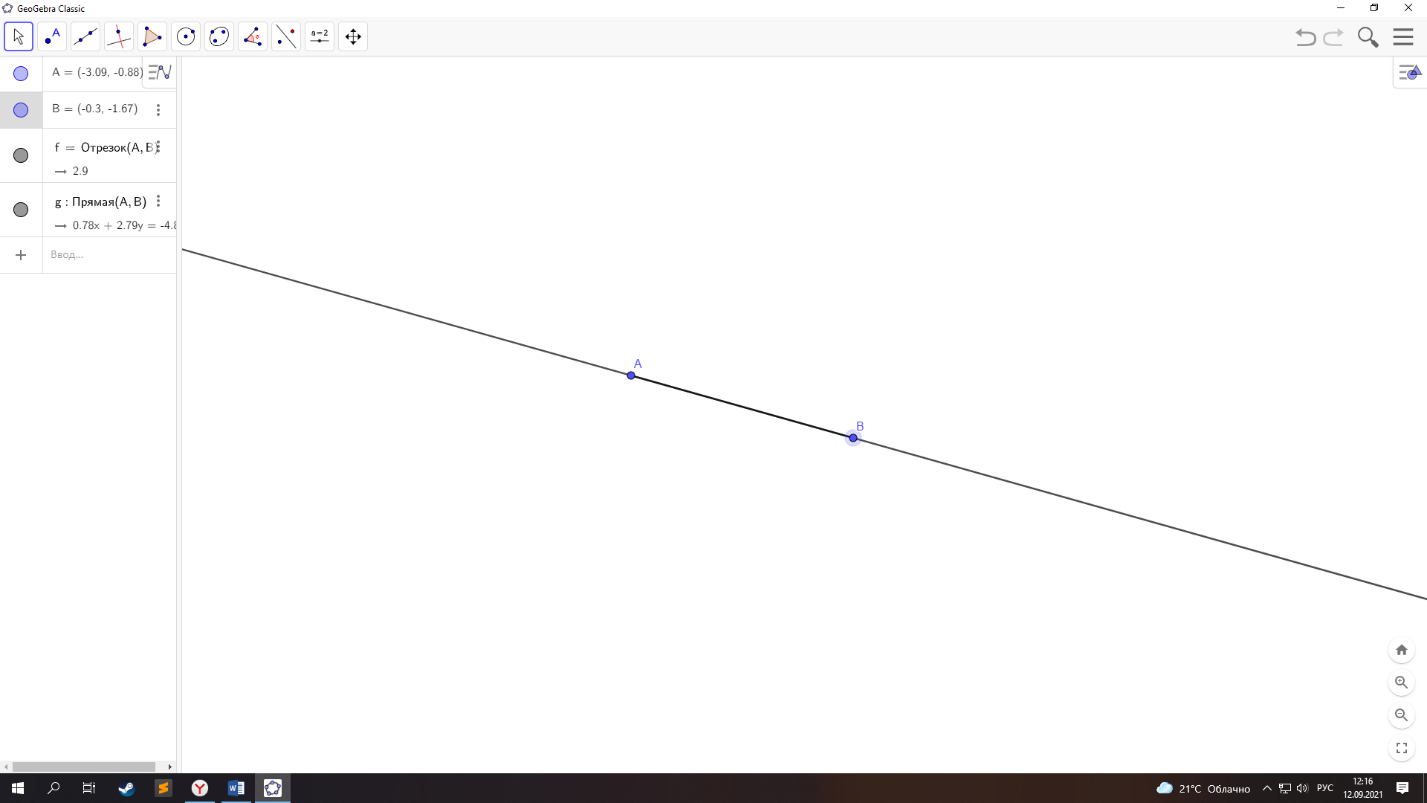
. Второй постулат геометрии: «ограниченную прямую можно непрерывно продолжать по прямой.» (см. рис. 1.2)
рис. 1.2
1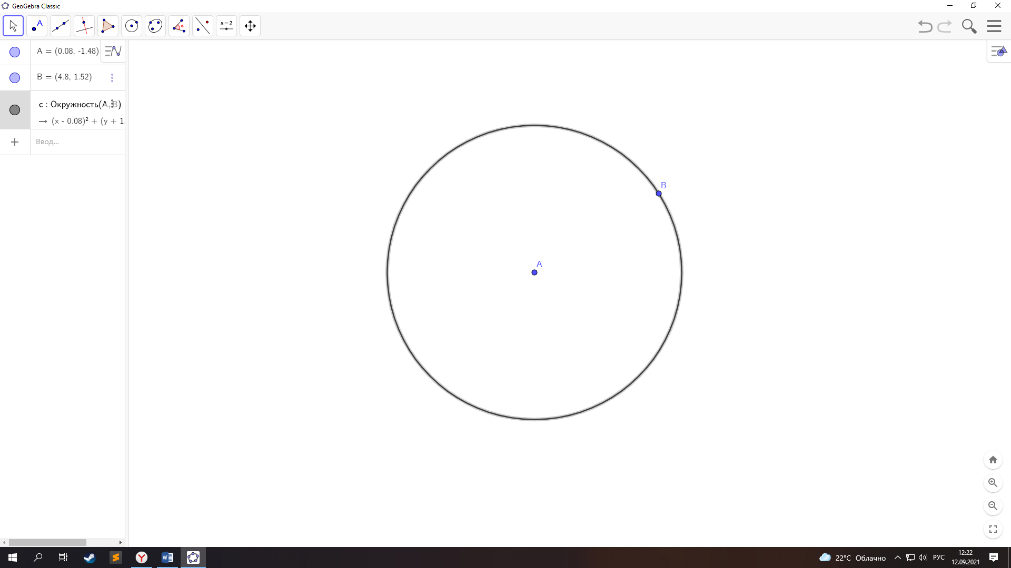 .3. Третий постулат геометрии: «из всякого центра всяким раствором может быть описан круг» (см. рис. 1.3)
.3. Третий постулат геометрии: «из всякого центра всяким раствором может быть описан круг» (см. рис. 1.3)
рис. 1.3
рис. 1.4
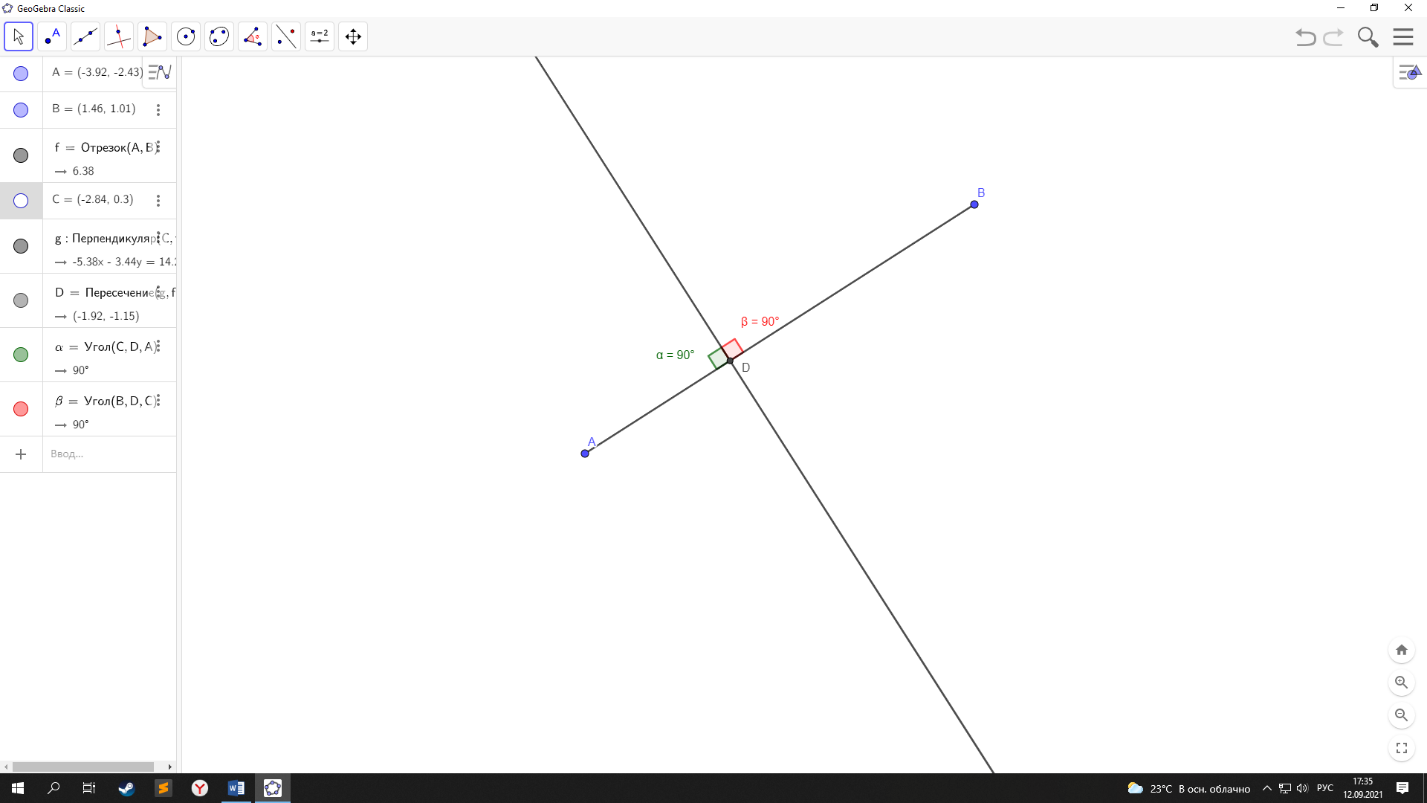
. Четвёртый постулат геометрии: «все прямые углы равны между собой» (см. рис. 1.4)
рис.1.5
.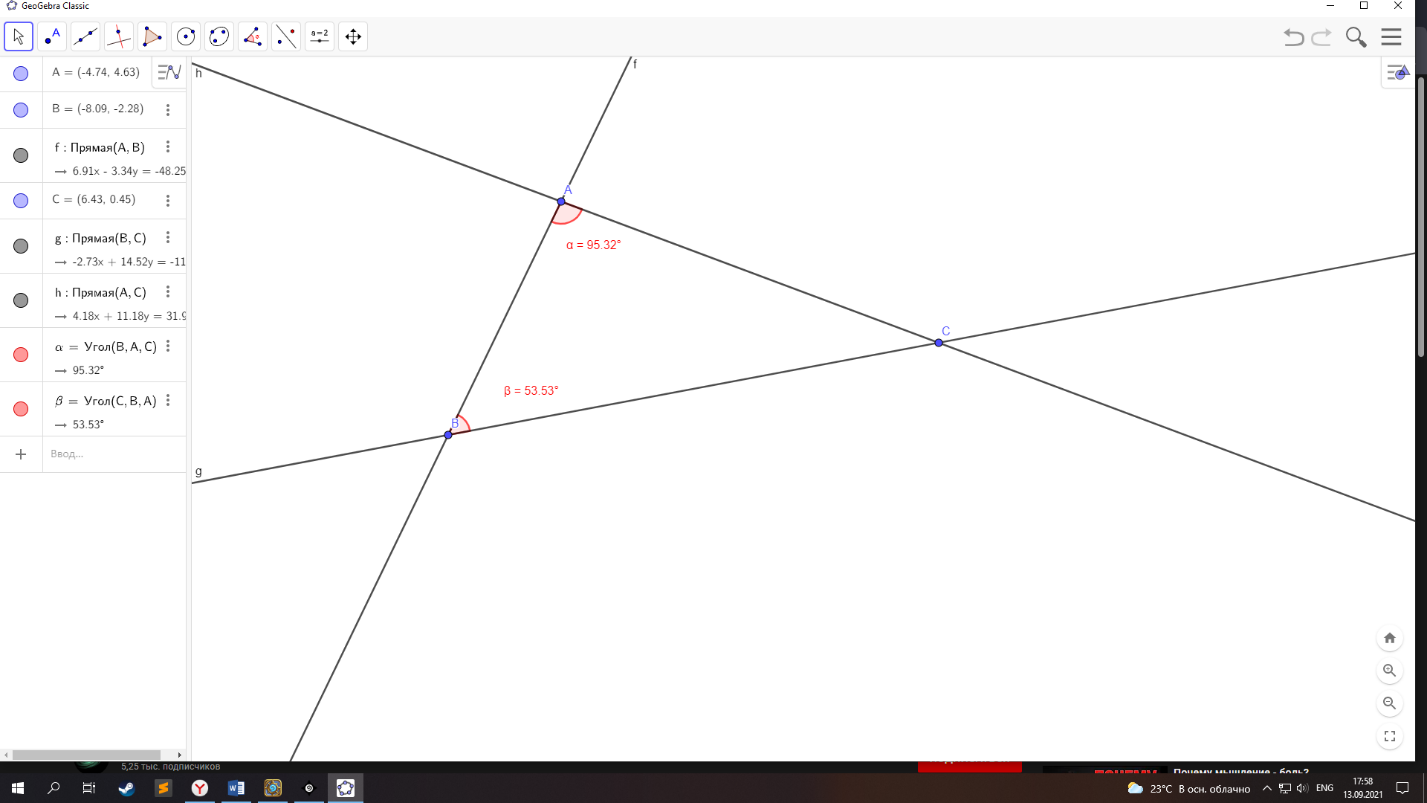 Пятый постулат геометрии: «если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых» (см. рис. 1.5)
Пятый постулат геометрии: «если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых» (см. рис. 1.5)
Но сложность, которую обнаружили Гаусс и другие математики, состояла не в самих рассуждениях, а в одном из этих пяти постулатах.
Никто не усомнился, что через 2 любые точки можно провести прямую или окружность. Однако пятый постулат не так очевиден (см. рис. 1.5). Это утверждение не такое простое, как остальные четыре, и когда речь идёт о получении точных знаний о мире недопустимо предполагать то, что не является истиной. Математики пытались доказать этот постулат (по сути, его пытались доказать, опираясь на первые четыре постулата). Но выяснилось, что доказательство некоторых теорем невозможно без пятого постулата. Нашлось множество допущений, эквивалентных пятому постулату.
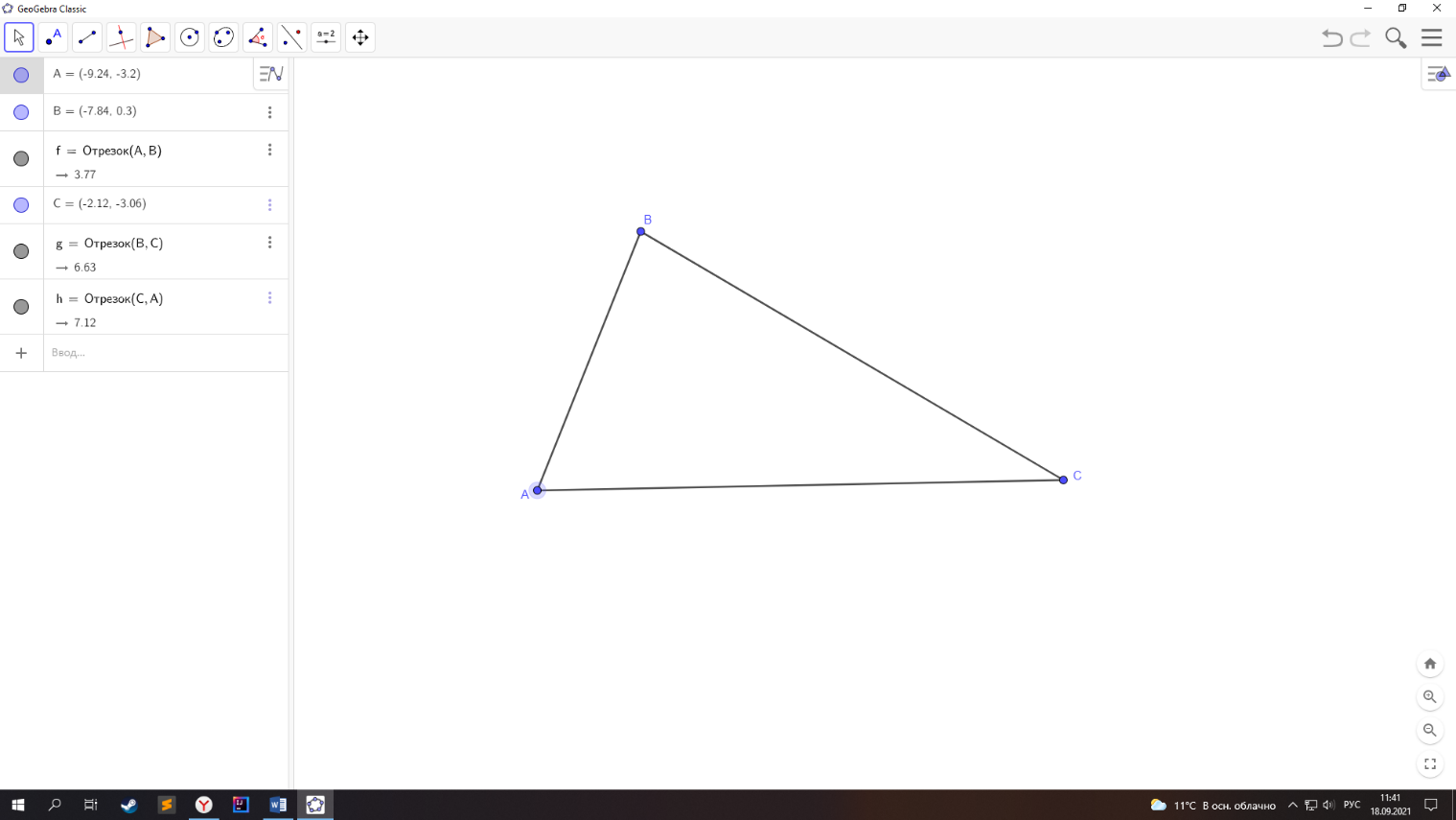
рис. 2.1
Например, рассмотрим сумму углов треугольника, используя пятый постулат.
Если предположить, что он верен, тогда мы проведём две параллельные прямые. Сумма односторонних углов будет равна 180º. Накрест лежащие углы будут равны.
рис. 2.3
Т
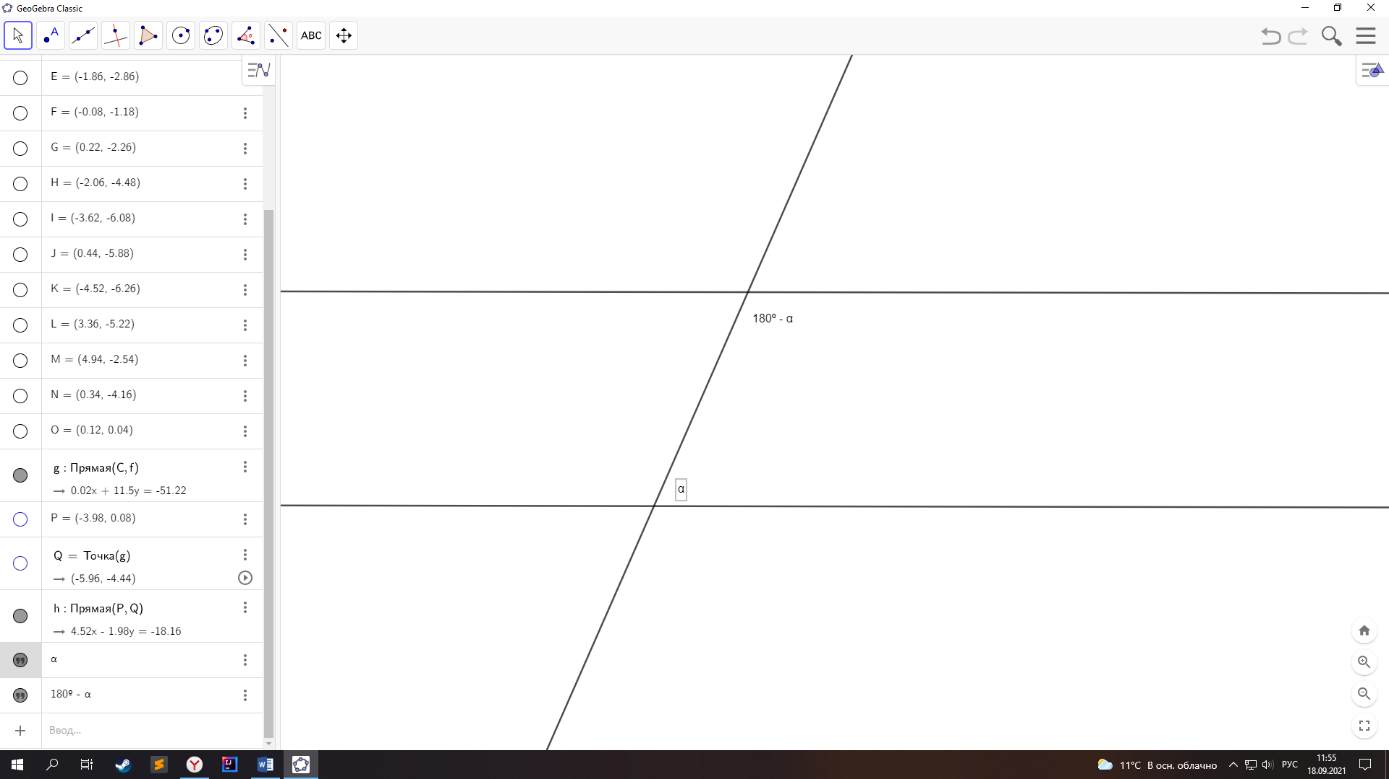
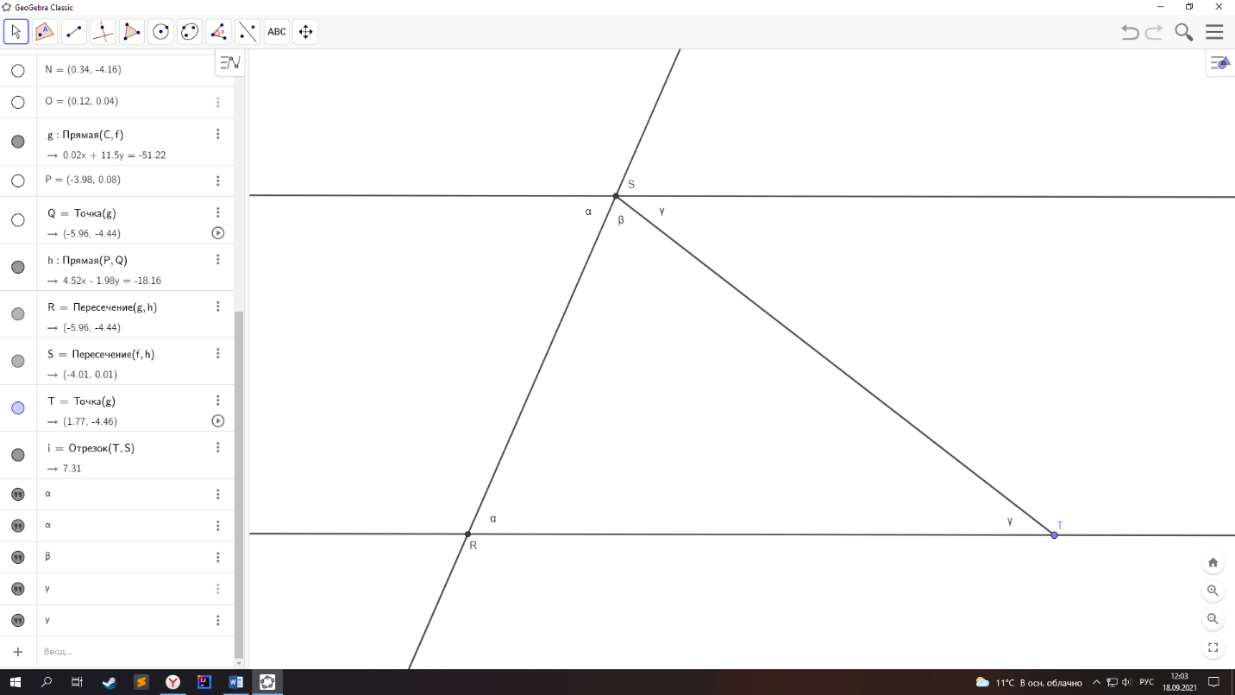
огда сумма углов треугольника будет равна 180º. И наоборот, если предположить, что сумма углов равна 180º, то можно вывести пятый постулат.
рис. 2.2
Н о это не то, чего добивались математики. Они хотели вывести пятый постулат, не делая никаких других допущений, кроме первых четырёх постулатов, они не хотели делать никаких других предположений, даже такое правдоподобное, как о сумме углов треугольника.
о это не то, чего добивались математики. Они хотели вывести пятый постулат, не делая никаких других допущений, кроме первых четырёх постулатов, они не хотели делать никаких других предположений, даже такое правдоподобное, как о сумме углов треугольника.
рис. 3.1
В 1733 году итальянский математик Джироламо Саккери сделал первый шаг вперёд. Он хотел понять: как бы выглядела геометрия, отличная от евклидовой? Он надеялся доказать невозможность такой геометрии. Очевидно, что если евклидова геометрия единственная и непротиворечивая, то она верна. Саккери обнаружил, что есть две другие геометрии. В каждой из них Саккери допустил первые четыре постулата геометрии, а для пятого придумал разные варианты.
В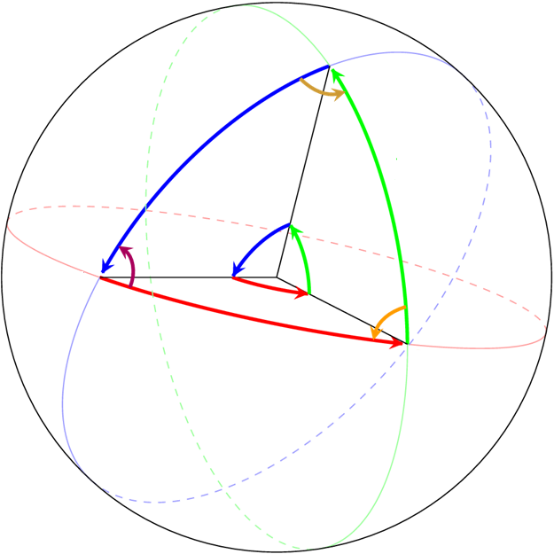 первой геометрии не существует параллельных прямых, поэтому любая прямая, проходящая через точку, не лежащую на данной прямой, пересекает её (см. рис. 3.1). В качестве примера можно рассмотреть глобус и параллели. Любые параллели пересекаются с экватором под прямым углом. Тем не менее все они пересекаются в северном и южном полюсах глобуса.
первой геометрии не существует параллельных прямых, поэтому любая прямая, проходящая через точку, не лежащую на данной прямой, пересекает её (см. рис. 3.1). В качестве примера можно рассмотреть глобус и параллели. Любые параллели пересекаются с экватором под прямым углом. Тем не менее все они пересекаются в северном и южном полюсах глобуса.
Существует целая геометрия, связанная с поверхностью сферы, называемая сферической геометрией, которая была довольно популярна в 18 веке. На сфере можно даже нарисовать треугольник, где каждая сторона – дуга главной окружности(см. рис. 3.2).
рис. 3.2
Но сферическая геометрия требует других постулатов, нежели в евклидовой геометрии, поэтому сферическая геометрия в качестве альтернативы не подошла Саккери. Был шанс, что она верна, но можно придумать другую геометрию.
О днако оказалось, что нельзя. Саккери доказал, что совокупность первых четырёх постулатов и этого свойства(см. рис. 3.1) не состоятельна и приводит к противоречию.
днако оказалось, что нельзя. Саккери доказал, что совокупность первых четырёх постулатов и этого свойства(см. рис. 3.1) не состоятельна и приводит к противоречию.
рис. 3.3
Во второй геометрии существует множество прямых, проходящих через точку, не лежащую на данной прямой и параллельных ей (см. рис. 3.3) (чтобы показать результат такой геометрии прямые на рисунке 3.3 изображены непараллельными данной прямой).
Опровергнуть эту геометрию оказалось намного сложнее, чем первую. Немецкий математик Иоганн Ламберт в 1770 году писал: «Я рассматривал следствия этой гипотезы, чтобы увидеть противоречива ли она. И из них я понял, что эта гипотеза так просто себя не разрушит».
В от к чему пришёлл Гаусс. Он читал книгу Ламберта, когда впервые поехал в Гёттинген и в 1775 поделился со своим предшественником верой в то, что если одна из этих альтернативных гипотез может прийти в противоречие с собой, то будет доказано, что евклидова геометрия верна. Но Ламберт обнаружил, что предложение может породить странные теоремы, не являющиеся, однако, противоречивыми. Например в этой геометрии сумма углов треугольника всегда меньше 180º или двух прямых углов (см. рис. 3.4), и фигуры разного размера не могут иметь одинакувую форму.
от к чему пришёлл Гаусс. Он читал книгу Ламберта, когда впервые поехал в Гёттинген и в 1775 поделился со своим предшественником верой в то, что если одна из этих альтернативных гипотез может прийти в противоречие с собой, то будет доказано, что евклидова геометрия верна. Но Ламберт обнаружил, что предложение может породить странные теоремы, не являющиеся, однако, противоречивыми. Например в этой геометрии сумма углов треугольника всегда меньше 180º или двух прямых углов (см. рис. 3.4), и фигуры разного размера не могут иметь одинакувую форму.
рис. 3.4
Неожиданно, но логически возможно. Постепенно Гаусс пришел к выводу, что эта альтернативная геометрия может быть логически непротиворечивой. Носреди всех, кто работал над этим вопросом он мало чего смог достичь. Чтобы узнать о математиках, которые внесли большой вклад в развитие альтернативных геометрий, перенесёмся из Европы в Венгрию и Россию.
Фаркаш Бойяи
С

туденческий друг Гаусса Фаркаш Бойяи (который всегда подписывался, как Вольфганг Бойяи) вернулся на родину в Венгрию и стал там профессором. Его сын Янош Бойяи оказался одарённым математиком. Он узнал о проблеме истинности геометрии от своего отца. «Я прошу тебя, оставь науку о параллельных прямых, я думал, что пожертвую собой ради истинны, я был готов сделаться мучеником этой истины, чтобы только подарить человечеству геометрию, очищенную от этого пятна. Я обернулся и увидел, что ни один человек не может пройти через этот мрак», - Сын не послушал отца и он попытался снова: «Я путешествовал, минуя все рифы этого бесконечного мёртвого моря, но всегда возвращался с поломанной мачтой и порванным парусом». Его сын ответил ему в 1823 году: «Я пока не сделал открытия, но тропа, по которой я иду, непременно приведёт меня у цели, при условии, что цель достижима. Всё, что я могу сказать сейчас – это то, что я создал новый иной мир из ничего. Всё, что я посылал тебе до этого было как карточный домик по сравнению с крепостью». В двух фразах я пока не сделал открытия и «я создал новый мир из ничего» целая история о том, что мы называем неевклидовой геометрией. На этот раз новая геометрия постижима и, возможно, она является истинной, ибо теперь истинность геометрии будет опираться на эксперимент, а геометрию можно будет поставить в один ряд с механикой.
Янош Бойяи
Н

о открытие ещё не было сделано, мы всё ещё можем прити к противоречию в любой момент. В 1831 году, несмотря на сомнения они опубликовали работу Яноша. Она вышла как приложение к книге отца по геометрии и её копию посали Гауссу, который ответил: «Если я начну со слов, что не могу похвалить эту работу, то ты наверняка удивишься, но я не могу сказать иначе, ведь похвалить эту работу, значит похвалить себя. По правде весь материал работы, путь, пройденный твоим сыном и результаты, к которым он пришёл, почти полностью совпадают с моими размышлениями». По понятным причинам Янош так и не простил Гаусса за то, что он посчитал попыткой одного из самых известных математиков того времени присвоить себе работы почти неизвестного учёного.

В России независимо от этих событий разворачивалась подобная история. Профессор математики Казанского университета Николай Иванович Лобачевский пытался доказать, что существует вторая, логически возможная геометрия. В 1829 году он опубликовал первое описание неевклидовой геометрии, за два года до публикации Яноша Бояйи. Но совершенно невозможно, чтобы Янош мог узнать о работе Лобачевского.
Николай Лобачевский
Но чего же достигли эти математики? Так как описания неевклидовой геометрии похожи разумно описывать эти работы одновременно. Так как их геометрия оказалась чем – то совершенно не похожим на евклидову геометрию, мы должны отринуть многие наши представления о мире и приготовиться ко входу в новую вселенную.
Глава I. Геометрия Лобачевского
Введение
К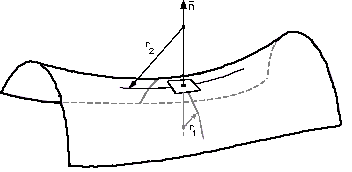 ривизна — это величина, характеризующая отклонение кривой (поверхности) в окрестности данной ее точки от касательной прямой (касательной плоскости).
ривизна — это величина, характеризующая отклонение кривой (поверхности) в окрестности данной ее точки от касательной прямой (касательной плоскости).
рис. 1.0.1
Кривизна Гаусса (или искривленность) обозначается K = k
1 * k
2, где k
1 — наибольшая главная кривизна, k
2 — наименьшая главная кривизна, k
1 и k
2 перпендикулярны друг к другу (см. 1.0.1). Главная кривизна k
i = 1/r
i. Искривленность K не изменяется при изгибании поверхности, то есть длины и углы кривых на ней остаются неизменными (это значит, что поверхность сделана из абсолютно нерастяжимого материала).
Если для некоторого пространства кривизна Гаусса K = 0, то мы имеем дело с пространством Евклида, в котором справедлива геометрия Евклида. При K 0 мы переходим к пространству и геометрии Римана (или сферической геометрии), которые имеют свои, отличные от евклидовой геометрии, законы. А при K
§1 Введение в геометрию Лобачевского. Аксиоматика
Геометрия Лобачевского (или гиперболическая геометрия) — одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных аксиомах, что и обычная евклидова геометрия, за исключением аксиомы о параллельных прямых, которая заменяется её отрицанием. Является одной из неевклидовых геометрий постоянной кривизны.
Евклидова аксиома о параллельных (точнее, одно из эквивалентных ей утверждений, при наличии других аксиом) может быть сформулирована следующим образом:
«На плоскости через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной.»
В геометрии Лобачевского вместо неё принимается следующая аксиома:
«Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.»
§2 Модели геометрии Лобачевского
Модели геометрии Лобачевского дали доказательство её непротиворечивости, точнее показали, что геометрия Лобачевского столь же непротиворечива, как геометрия Евклида.
Сам Лобачевский дал основы своей аналитической геометрии, и тем самым он уже фактически наметил такую модель. Он также заметил, что орисфера в пространстве Лобачевского изометрична евклидовой плоскости, тем самым фактически предложил обратную модель. Тем не менее, само понятие о модели прояснилось в работах Бельтрами и других.
В 1868 году выходит статья Бельтрами об интерпретациях геометрии Лобачевского. Бельтрами определил метрику плоскости Лобачевского и доказал, что она имеет всюду постоянную отрицательную кривизну.
Модели геометрии Лобачевского:
Псевдосфера
Псевдосфера (или поверхность Бельтрами) — поверхность постоянной отрицательной кривизны, образуемая вращением трактрисы около её асимптоты. Название подчёркивает сходство и различие со сферой, которая является примером поверхности с кривизной, также постоянной, но положительной.
рис 1.2.1
Т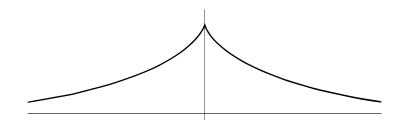 рактриса – плоская кривая, для которой длина отрезка касательной от точки касания до точки пересечения является постоянной величиной.
рактриса – плоская кривая, для которой длина отрезка касательной от точки касания до точки пересечения является постоянной величиной.
Характеристики псевдосферы:
то параметрическими уравнениями псевдосферы будут
Гауссова кривизна псевдосферы постоянна и равна 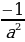
Площадь обоих раструбов псевдосферы совпадает с площадью сферы 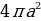
Объём равен половине объёма шара 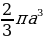
Проективная модель
П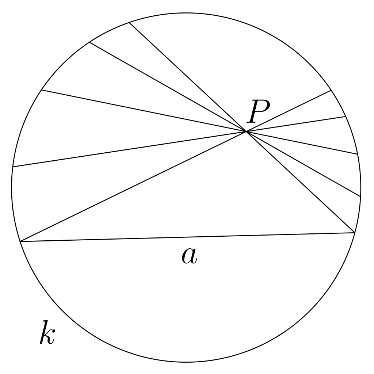 роективная модель (модель Клейна, модель Бельтрами — Клейна) — модель геометрии Лобачевского, предложена итальянским математиком Эудженио Бельтрами. Немецкий математик Феликс Клейн разработал её независимо.
роективная модель (модель Клейна, модель Бельтрами — Клейна) — модель геометрии Лобачевского, предложена итальянским математиком Эудженио Бельтрами. Немецкий математик Феликс Клейн разработал её независимо.
рис. 1.2.2
С её помощью доказывается непротиворечивость геометрии Лобачевского в предположении непротиворечивости евклидовой геометрии.
В этой модели плоскость представляет собой диск, ограниченный окружностью, также называемой абсолютом (точки абсолюта не принадлежат плоскости).
Прямая в такой модели – хорда абсолюта. Хорды, имеющие общую точку, соответствуют параллельным прямым.
Факт условной ограниченности плоскости позволяет провести через точку не лежащей на данной прямой бесконечно много прямых, не пересекающих её (рис. 1.2.2).
Расстояние между двумя точками A и B, лежащими на хорде A1 B1 в такой модели определяется по следующей формуле:
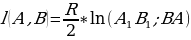 , где R – кривизна плоскости Лобачевского, а (A1 B1; BA) – двойное отношение.
, где R – кривизна плоскости Лобачевского, а (A1 B1; BA) – двойное отношение.
Важно заметить, что в такой модели любой факт евклидовой геометрии, кроме аксиомы о параллельных прямых, будет верен.
К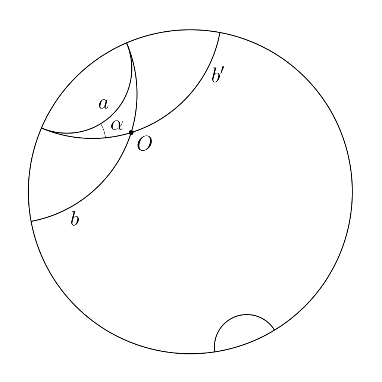 онформно-евклидова модель, модель Пуанкаре
онформно-евклидова модель, модель Пуанкаре
За плоскость в данной модели принимается внутренность окружности, а сама окружность, аналогично предыдущей модели называется абсолютом (для пространства моделью является шар).
рис. 1.2.3
Роль «прямых» в данной системе принимают на себя внутренние дуги окружности, перпендикулярные абсолюту (рис. 1.2.3).
Метрикой ds в конформно – евклидовой модели называется:
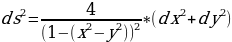 , где x, y – оси абсцисс и ординат соответственно
, где x, y – оси абсцисс и ординат соответственно
Если на дуге A1, B1 лежат точки A, B, то расстоянием между ними будет равно:
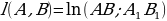 , где (AB; A1B1) – двойное отношение.
, где (AB; A1B1) – двойное отношение.
Таким образом на примере геометрии Лобачевского мы убедились в возможности неевклидовых геометрий, а также в её значительных отличиях от классической.
Глава II. Сферическая геометрия
§1 Введение в сферическую геометрию. Аксиоматика.
Сферическая геометрия – раздел геометрии, изучающий фигуры на поверхности сферы. Она возникла ещё в древности в связи с потребностями географии и астрономии. Является одной из неевклидовых геометрий постоянной кривизны.
Рассмотрим базовые понятия и аксиомы:
Большой круг – круг который делит сферу на две равных полусферы. Очевидно, что центр сферы совпадает с центром большого круга.
Через любые две точки сферы кроме диаметрально противоположных можно провести единственный большой круг.
Через две диаметрально противоположные точки можно провести бесконечно много больших кругов.
Любые два больших круга пересекаются по прямой, проходящей через центр окружности.
рис 2.1.1
Окружности двух больших кругов пересекаются в диаметрально противоположных точках.
П ри пересечении двух больших кругов образуется четыре сферический двуугольника (см. рис. 2.1.1), площадь каждого из которых вычисляется по формуле:
ри пересечении двух больших кругов образуется четыре сферический двуугольника (см. рис. 2.1.1), площадь каждого из которых вычисляется по формуле: 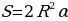 , где R – радиус сферы, а
, где R – радиус сферы, а 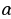 – угол двуугольника в радианах.
– угол двуугольника в радианах.
рис 2.1.2
Три больших круга, не пересекающихся в одной точке образуют восемь сферических треугольников (см. рис. 2.1.2). Сферический треугольник, стороны которого меньше половины большого круга, называется эйлеровым. Признаки равенства треугольников из евклидовой геометрии, действительны и в сферической геометрии. К ним добавляется четвёртый признак равенства треугольников, согласно которому два сферических треугольника равны, если углы одного соответственно равны углам другого.
Стороны сферического треугольника измеряются величиной угла, образованного радиусами, проведёнными из центра сферы к концам этой стороны. Каждая сторона сферического треугольника меньше суммы и больше разности двух других сторон. Сумма сторон сферического треугольника всегда меньше 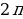 . Сумма углов
. Сумма углов 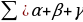 всегда меньше
всегда меньше 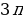 и больше
и больше 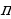 . Величина
. Величина 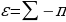 называется сферическим избытком и используется в формуле Жирара для нахождения площади сферического треугольника
называется сферическим избытком и используется в формуле Жирара для нахождения площади сферического треугольника 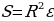 .
.
В сферической геометрии также видоизменяются соотношения между тригонометрическими функциями. Рассмотрим прямоугольный треугольник ABC, тогда справедливы следующие соотношения:
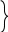

теорема косинусов
Справедливы также теоремы косинусов и синусов:
Заметим, что первая и вторая форма записи теоремы косинусов двойственны по отношению друг к другу. Теорема синусов двойственна сама к себе.
§2 Сферический треугольник.
рис 2.2.1
С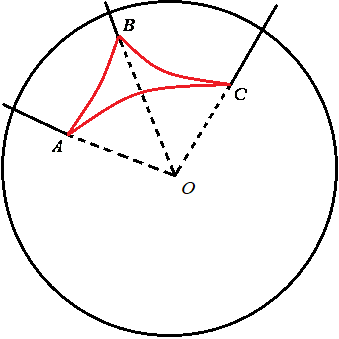 реди всех сферических многоугольников наибольший интерес представляет сферический треугольник. Рассмотрим его подробнее. Как мы заметили в пункте 7 §1 три больших окружности, пересекаясь попарно в двух точках, образуют восемь сферических треугольников. Зная стороны и углы хотя бы одного из них, можно определить элементы все остальных, поэтому рассматривают соотношения между элементами у того треугольника, у которого все стороны меньше половины большой окружности. Стороны треугольника измеряются плоскими углами трехгранного угла
реди всех сферических многоугольников наибольший интерес представляет сферический треугольник. Рассмотрим его подробнее. Как мы заметили в пункте 7 §1 три больших окружности, пересекаясь попарно в двух точках, образуют восемь сферических треугольников. Зная стороны и углы хотя бы одного из них, можно определить элементы все остальных, поэтому рассматривают соотношения между элементами у того треугольника, у которого все стороны меньше половины большой окружности. Стороны треугольника измеряются плоскими углами трехгранного угла 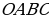 (см. рис 2.2.1), а углы треугольника – двугранными углами того же трехгранного угла.
(см. рис 2.2.1), а углы треугольника – двугранными углами того же трехгранного угла.
Сферический треугольник сохраняет большинство свойств планиметрического треугольника например: признаки равенства треугольников или неравенство треугольника, которое в условиях сферической геометрии гласит, что любой плоский угол сферического треугольника меньше суммы двух других.
Множество точек, равноудалённых от концов отрезка, будет существовать и на сфере, и образованная прямая будет перпендикулярна данному отрезку. Несложно доказать, что серединные перпендикуляры к сторонам сферического треугольника пересекаются в двух диаметрально противоположных точках 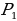 и
и 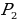 , которые будут являться полюсами его единственной описанной окружности. Легко заметить, что вокруг треугольника, а значит и трёхгранного угла можно описать единственный конус. Легко перенести на сферу и теорему о том, что биссектрисы сферического треугольника пересекаются в центре описанной около этого треугольника окружности.
, которые будут являться полюсами его единственной описанной окружности. Легко заметить, что вокруг треугольника, а значит и трёхгранного угла можно описать единственный конус. Легко перенести на сферу и теорему о том, что биссектрисы сферического треугольника пересекаются в центре описанной около этого треугольника окружности.
§3 Сферическая система координат.
рис 2.3.1
В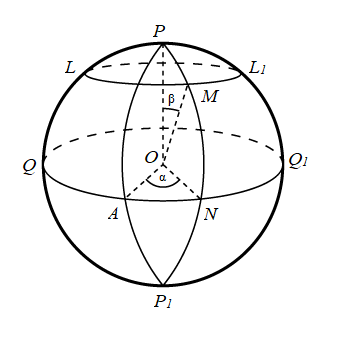 планиметрии мы пользуемся привычной для нас декартовой системой координат. На сфере мы будем использовать систему координат, также использующую две координаты, но имеющих другой смысл. Если в планиметрии координаты были связаны с расстоянием, то с сферической системе координат они связаны с углами. Рассмотрим рисунок 2.3.1. Зафиксируем экватор QQ1. Тогда первой координатой будет угол POM (высота точки М), и угол AOM (угол между нулевым меридианом и меридианом, проходящим через точку M (отсчитывается против часовой стрелки)).
планиметрии мы пользуемся привычной для нас декартовой системой координат. На сфере мы будем использовать систему координат, также использующую две координаты, но имеющих другой смысл. Если в планиметрии координаты были связаны с расстоянием, то с сферической системе координат они связаны с углами. Рассмотрим рисунок 2.3.1. Зафиксируем экватор QQ1. Тогда первой координатой будет угол POM (высота точки М), и угол AOM (угол между нулевым меридианом и меридианом, проходящим через точку M (отсчитывается против часовой стрелки)).
Заметим, что такая система координат применяется в географии.
Примечание: Более общим случаем сферической геометрии является геометрия Римана (или эллиптическая геометрия) – одна из неевклидовых геометрий постоянной положительной кривизны.
В геометрии Римана, как и в евклидовой геометрии прямая задаётся двумя точками, плоскость тремя точками, две плоскости пересекаются по прямой. Основным отличием геометрии Римана от евклидовой является факт отсутствия параллельных прямых.
Из – за своей сложности геометрия Римана в проекте рассмотрена не будет.
Глава III. Практическое применение неевклидовых геометрий.
§1 Применение сферической геометрии
Как мы уже знаем сферическая геометрия возникла в связи с практическими задачами. Первыми ей воспользовались астрономы, а затем путешественники и мореплаватели, ориентировавшиеся по звёздам. Поскольку было очень удобно, чтобы Солнце, Луна, звёзды вращались по воображаемой сфере, то для их изучения потребовались знания геометрии на сфере. Также очень давно появилась гипотеза о шарообразности Земли. Поэтому для вычисления географических координат, определения курса корабля, составления карт также требовались знания сферы.
В настоящее время сферическая геометрия особенно широкое применение находит в астрономии и геодезии (науке о форме и размерах Земли), навигации и картографии. Так же, как и в планиметрии, в сферической геометрии рассматриваются точки и прямые, расстояния между точками, перемещения.
Рассмотрим практическую задачу: представим, что нам потребовалось найти расстояние между двумя точками Земли. Заметим, что привычными формулами, применимыми в евклидовом пространстве пользоваться нельзя. Рассмотрим редко используемые тригонометрические функции:
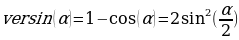 - версинус
- версинус
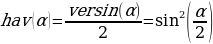 - гаверсинус
- гаверсинус
Тогда будет справедлива следующая формула:
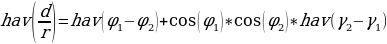 , где:
, где:
d – это центральный угол между двумя точками, лежащими на большом круге
r – радиус сферы
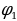 и
и 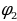 – широта первой и второй точек в радианах
– широта первой и второй точек в радианах
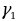 и
и 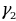 – долгота первой и второй точек в радианах
– долгота первой и второй точек в радианах
Для решения задачи выполним некоторые преобразования:
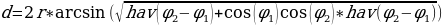
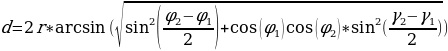
Теперь применим полученную формулу в реальной задаче. Найдём расстояние между памятником В.И. Ленину в Тамбове и Спасской башней в Москве.
Переведём градусы в радианы и подставим в формулу:
координаты памятника Ленину: 0.919694 и 0.723127
координаты Спасской башни: 0.972574 и 0.656290
 =419.042620
=419.042620
Примечание: все подсчёты выполнены с точностью до 6 знаков после запятой.
Для упрощения будущих подсчётов и получения большей точности приведём несложную программу на языке программирования Python.
Пример реализации расчётов на языке Python
 Заметим также что мы не принимали во внимание тот факт, что Земля не является идеальной сферой, а потому мы получили результат с погрешностью ±0,5%.
Заметим также что мы не принимали во внимание тот факт, что Земля не является идеальной сферой, а потому мы получили результат с погрешностью ±0,5%.
§2 Применение геометрии Лобачевского
Сам Лобачевский использовал свою геометрию для вычисления определённых интегралов. Также геометрия помогла построить теорию автоморфных функций (функций, не изменяющих своих значений, если их аргумент подвергнуть комплексно-аналитическим преобразованиям). Новая геометрия стала отправной точкой исследований Пуанкаре, который писал: «…неевклидова геометрия есть ключ к решению всей задачи…».
Применение геометрии Лобачевского нашли и физики: была установлена связь геометрии Лобачевского с частной теорией относительности. Рассмотрим закон распространения света:
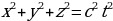 , где x, y, z – координаты, c – скорость света, t – время движения
, где x, y, z – координаты, c – скорость света, t – время движения
При делении обоих частей уравнения на 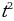 получим:
получим:
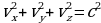
т.е. уравнение сферы в пространстве скоростей.
Из этого уравнения следует, что по поверхности сферы может двигаться только свет (т.е. со скорость света с), а все остальные скорости лежат внутри сферы, а так как внутренне пространство сферы имеет отрицательную кривизну, то для скоростей, меньших скорости света имеет место геометрия Лобачевского. Например, в теории относительности сложение скоростей равносильно сложению отрезков в геометрии Лобачевского.
Геометрия Лобачевского нашла ещё одно применение в теории относительности: если предположить, что распределение масс в космосе равномерно (а такое приближение в космических масштабах уместно), то оказывается, что пространство построено по принципам геометрии Лобачевского. Проиллюстрируем это мысленным экспериментом: допустим, что мы имеем натянутую ткань, подвешенную в воздухе, на которой покоится шар, вес которого не растягивает поверхность ткани. Положим на ткань материальную точку, вес которой способен вызвать провисание ткани. В таком случае мы получили модель, схожую с моделью чёрной дыры. Заметим, что в таком «провисании» кривизна пространства отрицательна, значит мы опять-таки имеем дело с геометрией Лобачевского.
Можно сделать вывод: несмотря на свою кажущуюся нереалистичность, геометрия Лобачевского применима в реальности.
§3 Неевклидовы геометрические тела
Тор
Рассмотрим такое геометрическое тело как тор:
Тор (или тороид) – тело, получаемое в результате вращения некоторой окружности вокруг некоторой прямой, лежащей в плоскости этой окружности, но не пресекающей её.
И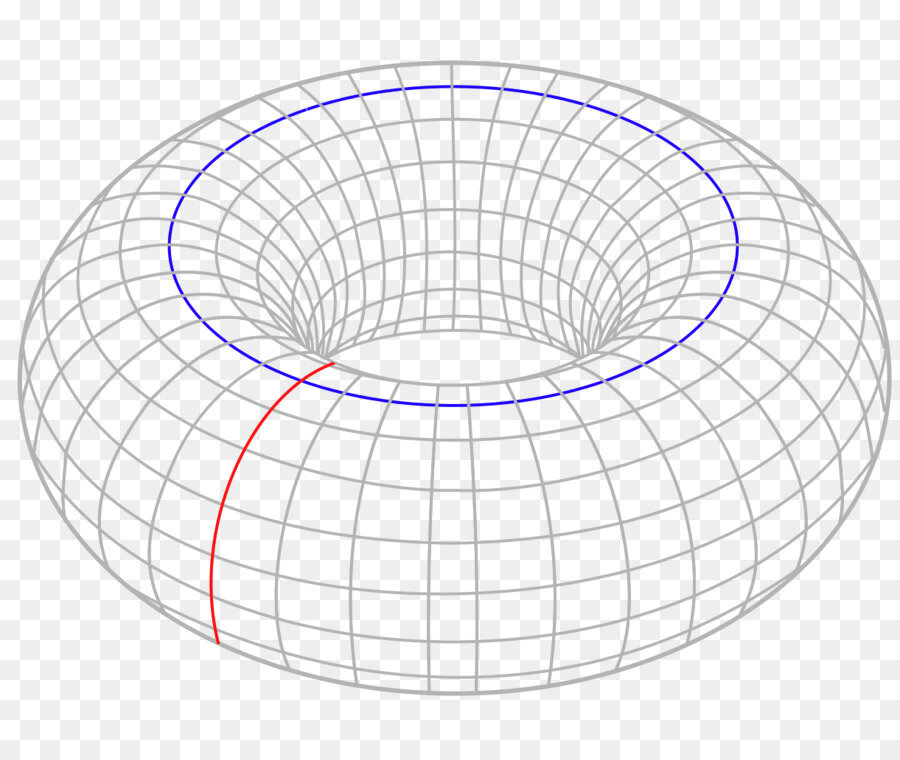 ногда в определении тора допускают, что прямая может касаться заданной окружности или даже пересекать её. Тогда получим 3 основных вида торов:
ногда в определении тора допускают, что прямая может касаться заданной окружности или даже пересекать её. Тогда получим 3 основных вида торов:
открытый – классический вариант тора, в этом случае прямая не пересекает и не касается заданной окружности.
рис. 3.3.1.1
Рис 3.3.1.2
рис 3.3.1.3
Рассмотрим уравнение, которым задаётся тор:
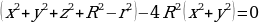 , где R – расстояние от цента тора до оси вращения, r – радиус образующей окружности.
, где R – расстояние от цента тора до оси вращения, r – радиус образующей окружности.
Перечислим основные свойства данного геометрического тела:
площадь поверхности тора равна: 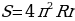
объём тора равен: 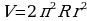
открытый тор можно вывернуть наизнанку непрерывным способом
два таких тора можно продеформировать так, что один тор поглотил второго
Т 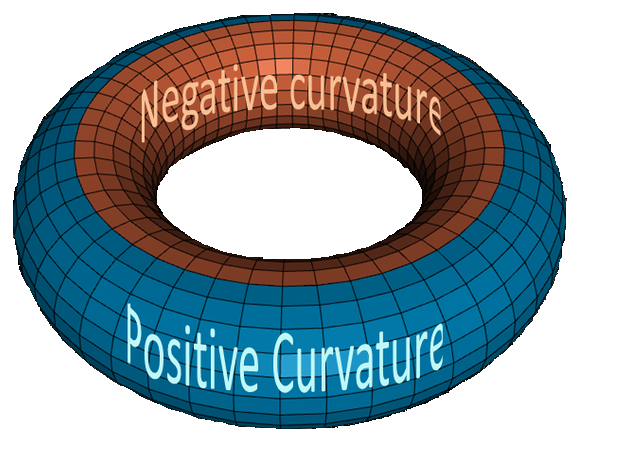 еперь рассмотрим необычность данного тела. Выберем линию нулевой кривизны (синяя линия на рис. 3.3.1.1), тогда внутренняя часть тора будет иметь отрицательную кривизну, а значит будет справедлива геометрия Лобачевского. С другой стороны, с внешней части тора кривизна положительна и там справедлива сферическая геометрия (геометрия Римана).
еперь рассмотрим необычность данного тела. Выберем линию нулевой кривизны (синяя линия на рис. 3.3.1.1), тогда внутренняя часть тора будет иметь отрицательную кривизну, а значит будет справедлива геометрия Лобачевского. С другой стороны, с внешней части тора кривизна положительна и там справедлива сферическая геометрия (геометрия Римана).
рис 3.3.1.3
Лента Мёбиуса
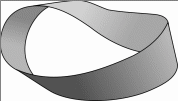
рис 3.3.2.1
Лента Мёбиуса – топологический непрерывный объект, который в классическом евклидовом пространстве является односторонним. Что же это значит? Для начала сделаем модель данного объекта. Возьмём достаточно длинную полоску бумаги и свернём её в кольцо, предварительно перевернув один из краёв. Получим похожее тело (см. рис 3.3.2.1).
Рассмотрим основные свойства ленты Мёбиуса:
границей ленты является непрерывная кривая
как мы уже знаем, в евклидовом пространстве она является односторонней. Проще всего проиллюстрировать это экспериментом. Возьмём ленту Мёбиуса и начнём чертить на ней линию не отрывая карандаша, мы сумеем начертить замкнутую линию. Отсюда следует, что мы можем соединить две любые точки на ней. Учитывая замечание из предыдущего пункта получим, что лента имеет единственную поверхность и единственную грань.
представим, что мы выбираем какую - то точку на ленте и начинаем идти по ней. Тогда после полного обхода его направление изменится на противоположное. Это означает, что условный человек, идущий по ленте Мёбиуса, вернётся в начальную точку, но в зеркальном отражении самого себя, таким образом по ленте Мёбиуса можно ходить бесконечно.
для геометрических тел существует понятие хроматического номера. Хроматический номер – максимально число областей, на которое можно раскрасить тело, так чтобы каждая из них имела общую сторону со всеми другими. Например, для обычного кольца это число равно 5. А вот для ленты Мёбиуса это число уже равно 6.
Лента Мёбиуса очень широко используется в физике и технике. Например, Никола Тесла изобрёл резистор в форме ленты, состоящий из двух скрученных проводящих поверхностей, это изобретение может сопротивляться току без создания электромагнитных помех. Некоторые конвейерные ленты устроены по принципу ленты Мёбиуса. Это позволяет значительно уменьшить износ деталей.
Примечание: до этого мы рассматривали ленту Мёбиуса в евклидовом пространстве, но также возможно рассмотрение этого тела в рамках известных нам геометрии Лобачевского и сферической геометрии. Тогда первоначальная форма (а в случае сферической геометрии даже полнота) ленты будет утеряна.
Заключение:
Мы рассмотрели основные виды неевклидовых геометрий и их историю. В процессе работы над проектом я закрепил на практике свои навыки геометрии, использовал программы для моделирования и черчения (Blender, Geogebra). Также пригодились мои навыки программирования для облегчения вычислений.
Список используемых источников:
Александров П. С. «Что такое неэвклидова геометрия» [Текст] М.: УРСС, 2007
www.krugosvet.ru Сферическая геометрия [Интернет ресурс]
https://bigenc.ru/mathematics/text/2177061 Геометрия Лобачевского [Интернет ресурс]
https://infourok.ru/razrabotka-elementi-sfericheskoy-geometrii-481724.html Элементы сферической геометрии [Интернет ресурс]
ru.wikipedia.org [Интернет ресурс]
Александров А. Д., Нецветаев Н. Ю. «Геометрия.» [Текст]— М.: Наука, 1990.
Клейн Ф. «Неевклидова геометрия.» [Текст] — М.—Л.: ОНТИ, 1936.
https://www.booksite.ru/fulltext/1/001/008/107/979.htm [Интернет ресурс]
https://dic.academic.ru/dic.nsf/ruwiki/1007718 [Интернет ресурс]
https://dgng.pstu.ru/conf2016/papers/10/ [Интернет ресурс]







 Примечание 1:
Примечание 1:
 .3. Третий постулат геометрии: «из всякого центра всяким раствором может быть описан круг» (см. рис. 1.3)
.3. Третий постулат геометрии: «из всякого центра всяким раствором может быть описан круг» (см. рис. 1.3) 
 Пятый постулат геометрии: «если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых» (см. рис. 1.5)
Пятый постулат геометрии: «если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых» (см. рис. 1.5) 

 огда сумма углов треугольника будет равна 180º. И наоборот, если предположить, что сумма углов равна 180º, то можно вывести пятый постулат.
огда сумма углов треугольника будет равна 180º. И наоборот, если предположить, что сумма углов равна 180º, то можно вывести пятый постулат.  о это не то, чего добивались математики. Они хотели вывести пятый постулат, не делая никаких других допущений, кроме первых четырёх постулатов, они не хотели делать никаких других предположений, даже такое правдоподобное, как о сумме углов треугольника.
о это не то, чего добивались математики. Они хотели вывести пятый постулат, не делая никаких других допущений, кроме первых четырёх постулатов, они не хотели делать никаких других предположений, даже такое правдоподобное, как о сумме углов треугольника. первой геометрии не существует параллельных прямых, поэтому любая прямая, проходящая через точку, не лежащую на данной прямой, пересекает её (см. рис. 3.1). В качестве примера можно рассмотреть глобус и параллели. Любые параллели пересекаются с экватором под прямым углом. Тем не менее все они пересекаются в северном и южном полюсах глобуса.
первой геометрии не существует параллельных прямых, поэтому любая прямая, проходящая через точку, не лежащую на данной прямой, пересекает её (см. рис. 3.1). В качестве примера можно рассмотреть глобус и параллели. Любые параллели пересекаются с экватором под прямым углом. Тем не менее все они пересекаются в северном и южном полюсах глобуса. днако оказалось, что нельзя. Саккери доказал, что совокупность первых четырёх постулатов и этого свойства(см. рис. 3.1) не состоятельна и приводит к противоречию.
днако оказалось, что нельзя. Саккери доказал, что совокупность первых четырёх постулатов и этого свойства(см. рис. 3.1) не состоятельна и приводит к противоречию. от к чему пришёлл Гаусс. Он читал книгу Ламберта, когда впервые поехал в Гёттинген и в 1775 поделился со своим предшественником верой в то, что если одна из этих альтернативных гипотез может прийти в противоречие с собой, то будет доказано, что евклидова геометрия верна. Но Ламберт обнаружил, что предложение может породить странные теоремы, не являющиеся, однако, противоречивыми. Например в этой геометрии сумма углов треугольника всегда меньше 180º или двух прямых углов (см. рис. 3.4), и фигуры разного размера не могут иметь одинакувую форму.
от к чему пришёлл Гаусс. Он читал книгу Ламберта, когда впервые поехал в Гёттинген и в 1775 поделился со своим предшественником верой в то, что если одна из этих альтернативных гипотез может прийти в противоречие с собой, то будет доказано, что евклидова геометрия верна. Но Ламберт обнаружил, что предложение может породить странные теоремы, не являющиеся, однако, противоречивыми. Например в этой геометрии сумма углов треугольника всегда меньше 180º или двух прямых углов (см. рис. 3.4), и фигуры разного размера не могут иметь одинакувую форму.  туденческий друг Гаусса Фаркаш Бойяи (который всегда подписывался, как Вольфганг Бойяи) вернулся на родину в Венгрию и стал там профессором. Его сын Янош Бойяи оказался одарённым математиком. Он узнал о проблеме истинности геометрии от своего отца. «Я прошу тебя, оставь науку о параллельных прямых, я думал, что пожертвую собой ради истинны, я был готов сделаться мучеником этой истины, чтобы только подарить человечеству геометрию, очищенную от этого пятна. Я обернулся и увидел, что ни один человек не может пройти через этот мрак», - Сын не послушал отца и он попытался снова: «Я путешествовал, минуя все рифы этого бесконечного мёртвого моря, но всегда возвращался с поломанной мачтой и порванным парусом». Его сын ответил ему в 1823 году: «Я пока не сделал открытия, но тропа, по которой я иду, непременно приведёт меня у цели, при условии, что цель достижима. Всё, что я могу сказать сейчас – это то, что я создал новый иной мир из ничего. Всё, что я посылал тебе до этого было как карточный домик по сравнению с крепостью». В двух фразах я пока не сделал открытия и «я создал новый мир из ничего» целая история о том, что мы называем неевклидовой геометрией. На этот раз новая геометрия постижима и, возможно, она является истинной, ибо теперь истинность геометрии будет опираться на эксперимент, а геометрию можно будет поставить в один ряд с механикой.
туденческий друг Гаусса Фаркаш Бойяи (который всегда подписывался, как Вольфганг Бойяи) вернулся на родину в Венгрию и стал там профессором. Его сын Янош Бойяи оказался одарённым математиком. Он узнал о проблеме истинности геометрии от своего отца. «Я прошу тебя, оставь науку о параллельных прямых, я думал, что пожертвую собой ради истинны, я был готов сделаться мучеником этой истины, чтобы только подарить человечеству геометрию, очищенную от этого пятна. Я обернулся и увидел, что ни один человек не может пройти через этот мрак», - Сын не послушал отца и он попытался снова: «Я путешествовал, минуя все рифы этого бесконечного мёртвого моря, но всегда возвращался с поломанной мачтой и порванным парусом». Его сын ответил ему в 1823 году: «Я пока не сделал открытия, но тропа, по которой я иду, непременно приведёт меня у цели, при условии, что цель достижима. Всё, что я могу сказать сейчас – это то, что я создал новый иной мир из ничего. Всё, что я посылал тебе до этого было как карточный домик по сравнению с крепостью». В двух фразах я пока не сделал открытия и «я создал новый мир из ничего» целая история о том, что мы называем неевклидовой геометрией. На этот раз новая геометрия постижима и, возможно, она является истинной, ибо теперь истинность геометрии будет опираться на эксперимент, а геометрию можно будет поставить в один ряд с механикой.  о открытие ещё не было сделано, мы всё ещё можем прити к противоречию в любой момент. В 1831 году, несмотря на сомнения они опубликовали работу Яноша. Она вышла как приложение к книге отца по геометрии и её копию посали Гауссу, который ответил: «Если я начну со слов, что не могу похвалить эту работу, то ты наверняка удивишься, но я не могу сказать иначе, ведь похвалить эту работу, значит похвалить себя. По правде весь материал работы, путь, пройденный твоим сыном и результаты, к которым он пришёл, почти полностью совпадают с моими размышлениями». По понятным причинам Янош так и не простил Гаусса за то, что он посчитал попыткой одного из самых известных математиков того времени присвоить себе работы почти неизвестного учёного.
о открытие ещё не было сделано, мы всё ещё можем прити к противоречию в любой момент. В 1831 году, несмотря на сомнения они опубликовали работу Яноша. Она вышла как приложение к книге отца по геометрии и её копию посали Гауссу, который ответил: «Если я начну со слов, что не могу похвалить эту работу, то ты наверняка удивишься, но я не могу сказать иначе, ведь похвалить эту работу, значит похвалить себя. По правде весь материал работы, путь, пройденный твоим сыном и результаты, к которым он пришёл, почти полностью совпадают с моими размышлениями». По понятным причинам Янош так и не простил Гаусса за то, что он посчитал попыткой одного из самых известных математиков того времени присвоить себе работы почти неизвестного учёного. 
 ривизна — это величина, характеризующая отклонение кривой (поверхности) в окрестности данной ее точки от касательной прямой (касательной плоскости).
ривизна — это величина, характеризующая отклонение кривой (поверхности) в окрестности данной ее точки от касательной прямой (касательной плоскости).  рактриса – плоская кривая, для которой длина отрезка касательной от точки касания до точки пересечения является постоянной величиной.
рактриса – плоская кривая, для которой длина отрезка касательной от точки касания до точки пересечения является постоянной величиной. 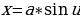
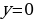
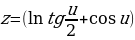 ,
, 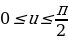
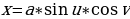
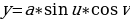
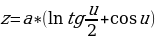 ,
, 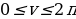
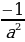
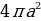
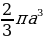
 роективная модель (модель Клейна, модель Бельтрами — Клейна) — модель геометрии Лобачевского, предложена итальянским математиком Эудженио Бельтрами. Немецкий математик Феликс Клейн разработал её независимо.
роективная модель (модель Клейна, модель Бельтрами — Клейна) — модель геометрии Лобачевского, предложена итальянским математиком Эудженио Бельтрами. Немецкий математик Феликс Клейн разработал её независимо.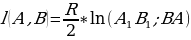 , где R – кривизна плоскости Лобачевского, а (A1 B1; BA) – двойное отношение.
, где R – кривизна плоскости Лобачевского, а (A1 B1; BA) – двойное отношение. онформно-евклидова модель, модель Пуанкаре
онформно-евклидова модель, модель Пуанкаре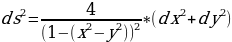 , где x, y – оси абсцисс и ординат соответственно
, где x, y – оси абсцисс и ординат соответственно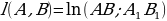 , где (AB; A1B1) – двойное отношение.
, где (AB; A1B1) – двойное отношение.
 ри пересечении двух больших кругов образуется четыре сферический двуугольника (см. рис. 2.1.1), площадь каждого из которых вычисляется по формуле:
ри пересечении двух больших кругов образуется четыре сферический двуугольника (см. рис. 2.1.1), площадь каждого из которых вычисляется по формуле: 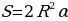 , где R – радиус сферы, а
, где R – радиус сферы, а 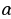 – угол двуугольника в радианах.
– угол двуугольника в радианах.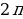 . Сумма углов
. Сумма углов 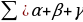 всегда меньше
всегда меньше 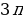 и больше
и больше 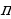 . Величина
. Величина 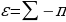 называется сферическим избытком и используется в формуле Жирара для нахождения площади сферического треугольника
называется сферическим избытком и используется в формуле Жирара для нахождения площади сферического треугольника 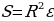 .
.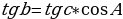
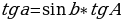
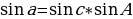
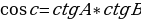
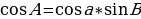
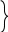

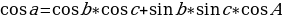
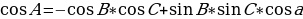
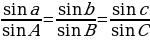 – теорема синусов
– теорема синусов реди всех сферических многоугольников наибольший интерес представляет сферический треугольник. Рассмотрим его подробнее. Как мы заметили в пункте 7 §1 три больших окружности, пересекаясь попарно в двух точках, образуют восемь сферических треугольников. Зная стороны и углы хотя бы одного из них, можно определить элементы все остальных, поэтому рассматривают соотношения между элементами у того треугольника, у которого все стороны меньше половины большой окружности. Стороны треугольника измеряются плоскими углами трехгранного угла
реди всех сферических многоугольников наибольший интерес представляет сферический треугольник. Рассмотрим его подробнее. Как мы заметили в пункте 7 §1 три больших окружности, пересекаясь попарно в двух точках, образуют восемь сферических треугольников. Зная стороны и углы хотя бы одного из них, можно определить элементы все остальных, поэтому рассматривают соотношения между элементами у того треугольника, у которого все стороны меньше половины большой окружности. Стороны треугольника измеряются плоскими углами трехгранного угла 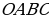 (см. рис 2.2.1), а углы треугольника – двугранными углами того же трехгранного угла.
(см. рис 2.2.1), а углы треугольника – двугранными углами того же трехгранного угла.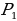 и
и 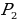 , которые будут являться полюсами его единственной описанной окружности. Легко заметить, что вокруг треугольника, а значит и трёхгранного угла можно описать единственный конус. Легко перенести на сферу и теорему о том, что биссектрисы сферического треугольника пересекаются в центре описанной около этого треугольника окружности.
, которые будут являться полюсами его единственной описанной окружности. Легко заметить, что вокруг треугольника, а значит и трёхгранного угла можно описать единственный конус. Легко перенести на сферу и теорему о том, что биссектрисы сферического треугольника пересекаются в центре описанной около этого треугольника окружности. планиметрии мы пользуемся привычной для нас декартовой системой координат. На сфере мы будем использовать систему координат, также использующую две координаты, но имеющих другой смысл. Если в планиметрии координаты были связаны с расстоянием, то с сферической системе координат они связаны с углами. Рассмотрим рисунок 2.3.1. Зафиксируем экватор QQ1. Тогда первой координатой будет угол POM (высота точки М), и угол AOM (угол между нулевым меридианом и меридианом, проходящим через точку M (отсчитывается против часовой стрелки)).
планиметрии мы пользуемся привычной для нас декартовой системой координат. На сфере мы будем использовать систему координат, также использующую две координаты, но имеющих другой смысл. Если в планиметрии координаты были связаны с расстоянием, то с сферической системе координат они связаны с углами. Рассмотрим рисунок 2.3.1. Зафиксируем экватор QQ1. Тогда первой координатой будет угол POM (высота точки М), и угол AOM (угол между нулевым меридианом и меридианом, проходящим через точку M (отсчитывается против часовой стрелки)).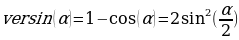 - версинус
- версинус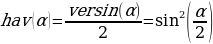 - гаверсинус
- гаверсинус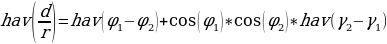 , где:
, где: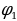 и
и 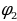 – широта первой и второй точек в радианах
– широта первой и второй точек в радианах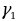 и
и 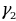 – долгота первой и второй точек в радианах
– долгота первой и второй точек в радианах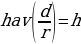
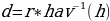
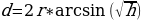
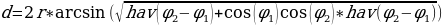
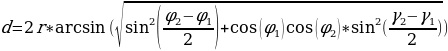
 =419.042620
=419.042620 Заметим также что мы не принимали во внимание тот факт, что Земля не является идеальной сферой, а потому мы получили результат с погрешностью ±0,5%.
Заметим также что мы не принимали во внимание тот факт, что Земля не является идеальной сферой, а потому мы получили результат с погрешностью ±0,5%.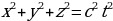 , где x, y, z – координаты, c – скорость света, t – время движения
, где x, y, z – координаты, c – скорость света, t – время движения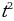 получим:
получим: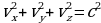
 ногда в определении тора допускают, что прямая может касаться заданной окружности или даже пересекать её. Тогда получим 3 основных вида торов:
ногда в определении тора допускают, что прямая может касаться заданной окружности или даже пересекать её. Тогда получим 3 основных вида торов: акрытые
акрытые торой вид достигается, когда прямая пересекает заданную окружность, в таком случае тор принимает следующую форму (рис. 3.3.1.3)
торой вид достигается, когда прямая пересекает заданную окружность, в таком случае тор принимает следующую форму (рис. 3.3.1.3)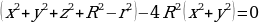 , где R – расстояние от цента тора до оси вращения, r – радиус образующей окружности.
, где R – расстояние от цента тора до оси вращения, r – радиус образующей окружности. 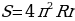
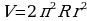
 еперь рассмотрим необычность данного тела. Выберем линию нулевой кривизны (синяя линия на рис. 3.3.1.1), тогда внутренняя часть тора будет иметь отрицательную кривизну, а значит будет справедлива геометрия Лобачевского. С другой стороны, с внешней части тора кривизна положительна и там справедлива сферическая геометрия (геометрия Римана).
еперь рассмотрим необычность данного тела. Выберем линию нулевой кривизны (синяя линия на рис. 3.3.1.1), тогда внутренняя часть тора будет иметь отрицательную кривизну, а значит будет справедлива геометрия Лобачевского. С другой стороны, с внешней части тора кривизна положительна и там справедлива сферическая геометрия (геометрия Римана). 










