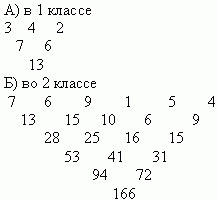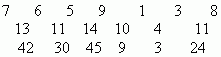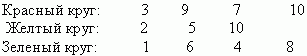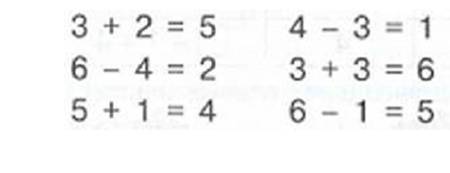Государственное учреждение образования
«Средняя школа №14 г.Новополоцка»
Методы и приёмы, способствующие формированию прочных вычислительных навыков у учащихся начальных классов
Подготовила:
учитель начальных
классов
Галай Ж. М.
Формирование вычислительных навыков - одна из главных задач, которая должна быть решена в ходе обучения детей в начальной школе. Эти навыки должны формироваться осознанно и прочно, так как на их базе строится весь начальный курс обучения математике.
В начальных классах особое место занимает работа по формированию навыков устных вычислений, поскольку в течение четырех лет обучения учащиеся должны не только сознательно усвоить приемы устных вычислений, но и приобрести твердые вычислительные навыки. Устные вычисления способствуют лучшему усвоению приемов письменных вычислений. т. к. последние включают в себе элементы устных вычислений.
Общеизвестно, что теоретической основой вычислительных приемов служат определения арифметических действий, свойства действий, и следствия, вытекающие из них. Имея это в виду можно выделить группы приемов вычислительных навыков в соответствии с их общей теоретической основой предусмотренной действующей программой по математике для начальных классов, что даст возможность использовать общие подходы в методике формирования соответствующих навыков.
Группы приемов:
1. Приемы, теоретическая основа которых — конкретный смысл
арифметических действий.
К ним относятся:
приемы сложения и вычитания чисел в пределах 10 для случаев вида а + 2, а + 3, а + 4, а + 0;
приемы табличного сложения и вычитания с переходом через десяток в пределах 20;
прием нахождения табличных результатов умножения;
прием нахождения табличных результатов деления.
2. Приемы, теоретической основой которых служат свойства арифметических действий.
К этой группе относится большинство вычислительных приемов.
Это приемы сложения и вычитания для случаев вида 53 ± 20, 47 ± 3, 30 – 6, 9 + 3, 12 – 3, 35 ± 7, 40 ± 23, 57 ± 32, 64 ± 18;
аналогичные приемы для случаев сложения и вычитания чисел больших, чем 100,
а также приемы письменного сложения и вычитания;
приемы умножения и деления для случаев вида 14 * 5, 5 * 14, 81 : 3, 18 * 40, 180 :20,
аналогичные приемы умножения и деления для чисел больших 100 и
приемы письменного умножения и деления.
Общая схема введения этих приемов одинакова: сначала изучаются соответствующие свойства, а затем на их основе вводятся приемы вычислений.
3. Приемы, теоретическая основа которых — связи между компонентами и результатами арифметических действий.
К ним относятся приемы для случаев вида 9 * 7, 21 : 3, 60 : 20, 54 : 18, 9 : 1, 0 : 6.
При введении этих приемов сначала рассматриваются связи между компонентами и результатом соответствующего арифметического действия, затем на этой основе вводится вычислительный прием.
4. Приемы, теоретическая основа которых — изменение результатов арифметических действий в зависимости от изменения одного из компонентов. Это приемы округления при выполнении сложения и вычитания чисел (46 + 19, 512 – 298) и приемы умножения и деления на 5, 25, 50. Введение этих приемов также требует предварительного изучения соответствующих зависимостей.
5. Приемы, теоретическая основа которых — вопросы нумерации чисел.
Это приемы для случаев вида а ± 1, 10 + 6, 16 – 10, 16 – 6, 57 * 10,1200 : 100; аналогичные приемы для больших чисел.
Введение этих приемов предусматривается после изучения соответствующих вопросов нумерации (натуральной последовательности, десятичного состава чисел,
позиционного принципа записи чисел).
6. Приемы, теоретическая основа которых — правила.
К ним относятся приемы для двух случаев: а * 1, а * 0. Поскольку правила
умножения чисел на единицу и нуль есть следствия из определения
действия умножения целых неотрицательных чисел, то они просто
сообщаются учащимся и в соответствии с ними выполняются вычисления.
Вычислительный навык - это высокая степень овладения вычислительными приёмами. Приобрести вычислительные навыки - значит, для каждого случая знать, какие операции и в каком порядке следует выполнять, чтобы найти результат арифметического действия и выполнять эти операции достаточно быстро.
Полноценный вычислительный навык характеризуется правильностью, осознанностью, рациональностью, обобщенностью, автоматизмом, прочностью.
Правильность - ученик правильно находит результат арифметического действия, то есть правильно выбирает и выполняет операции, составляющие приём.
Осознанность - ученик осознает, на основе каких знаний выбраны операции и установлен порядок их выполнения, в любой момент может объяснить, как он решал и почему так можно решать.
Рациональность - ученик выбирает для данного случая более рациональный приём, то есть выбирает те из возможных операций, выполнения которых легче других и быстрее приводит к результату.
Обобщенность - ученик может применить приём вычисления к большому числу случаев, то есть способен перенести приём вычисления на новые случаи.
Автоматизм - ученик выполняет и выделяет операции быстро и в свернутом виде, но всегда может вернуться к объяснению выбора системы операций. Высокая степень автоматизации должна быть достигнута по отношению к табличным случаям сложения и вычитания, умножения и деления.
Прочность - ученик сохраняет сформированные вычислительные навыки на длительное время.
На формирование вычислительных навыков большое влияние оказывает навыки беглого устного счёта. Проведение устного счёта в начале урока активизирует мыслительную деятельность, развивает память, внимание, автоматизирует навык.
Перед учителями встаёт вопрос, как сделать привычную и, казалось бы, однообразную работу интересной и увлекательной. Младшие школьники, обладая огромной энергией, стремлением к знаниям, не имеют того трудолюбия, усидчивости, внимания, которые так необходимы педагогу для организации учебного процесса. Именно это и заставляет учителей постоянно придумывать что-то новое, совершенствовать уже известное.
Присутствие в вычислительных упражнениях элемента занимательности, игры, догадки, сообразительности, использование интересного наглядного материала – вот те основные приёмы активизации познавательной деятельности, реализация которых позволит решить в практике обучения и задачу формирования прочных вычислительных навыков, и задачу развития познавательных способностей учащихся.
Остановлюсь на некоторых из них.
Важным звеном формирования вычислительных навыков являются математические игры.
1. Игра “Куча мала”.
Ученикам предлагается запомнить сначала 3, а затем 5, 6,7 чисел.Учитель называет числа один раз, а ученики записывают их. После знакомства с таблицей сложения ученики складывают последовательно каждые два числа.Например:
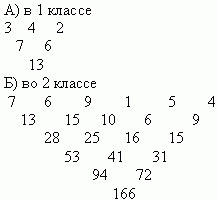
2. Игра “Три дорожки Ильи Муромца.
В игре используются знания таблицы умножения.
1-я дорожка: ученики записывают названный ряд чисел;2-я дорожка: учащиеся поочередно складывают числа первого ряда;3-я дорожка: ученики перемножают числа первого ряда. Например:
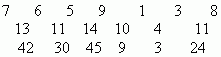
3. Игра “ Математические цепочки”.
Например:
А) Детеныши, какого животного еще слепые, а уже умеют защищаться от врагов.
Крот – 1, Еж – 0, Волк – 2
1х7 + 3 – 10 = ?
Б) Это растение каждой бродячей собаке радо. Даже лис, медведей и волков не боится. Они дерут его клыками, когтями рвут, а растение за них цепляется – расстаться с ними не может. Что это за растение?
Мокрица – 3, Молодило – 2, Репейник – 1
8х1 + 2 – 9 = ?
4. Игра “ Светофорик”.
Учитель прикрепляет к доске три круга: красный, желтый, зеленый. Рядом с ними записывает числа.
Например:
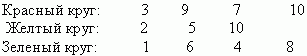
На парте у каждого ученика лежит комплект из трех кружков – огней светофора. Учитель называет пример: “8 плюс 2”. По команде учителя “Приготовились!” учащиеся решают пример и по команде “Включили!” показывают учителю соответствующий кружок.
5. Игра “Математическая мозаика”.
У каждого ученика имеется карточка с записанными на ней числами. Учитель диктует задание, ученик считает и закрашивает полученное число, в результате, если все задания выполнены верно, получается цифра 5
| | 32 | 45 | 35 | |
| 49 | 5 | 12 | | |
| | 10 | 40 | 8 | 80 |
| 90 | 21 | | 6 | 72 |
| | 64 | 81 | 7 | |
Например: 5 х 7.
Увеличь 9 в 5 раз.
Первый множитель 8, второй множитель 5.
Найди произведение 9 х 9.
Какое число надо умножить на 6, чтобы получить 42.
Уменьши 32 на 4.
Во сколько раз 5 меньше 30.
Делимое 35, делитель 7. Чему равно частное.
Увеличь 8 в 8 раз.
8 х 4.
Во сколько раз 45 больше 9
6. Задание типа “Тучка” дети готовят на перемене сами. На уроке
вписываем в тучку примеры с определённым ответом.

7. Хорошим помощником в проведении устного счёта является игра “Молчанка”, использование которой на уроках традиционно. Предлагаю свои варианты подобных заданий. Традиционные перфокарты связываю с известными детям литературными персонажами, героями мультфильмов, весёлыми человечками. Выполнение таких заданий сопровождается эмоциональным откликом детей.


Задания вычислительного характера сопровождаю игровыми сюжетами и рисунками. Например:
• Кеша в недоумении, он не знает, как выполнить задание.
Помогите ему!
8.Разнообразие форм кроссвордов, разных уровней сложности позволяет длительное время поддерживать интерес к выполнению данного вида работы.

Элементы занимательности и новизны, игры, встречи с любимыми героями, несложные, но интересные наглядные пособия вызывают у детей чувство удивления, радости, интерес к работе. Ученики чаще проявляют активность, находчивость, сообразительность и вместе с учителем добиваются высоких результатов.
Задания с многовариантными решениями.
Многовариантные задания - это система упражнений, выполнение которых поможет глубоко и осознано усвоить правило и выработать необходимый вычислительный навык на его основе.
Задание 1. Запиши число 30 тремя одинаковыми цифрами и знаками действий.
Постарайся найти несколько разных решений.
Задания с элементами занимательности.
Такие задания, в основном, направлены на отработку вычислительных навыков. Элемент занимательности увлекает детей, они стремятся выполнить все действия правильно и посмотреть к чему это приведет.
"Магические или занимательные квадраты" - это занимательная форма тренировки в сложении вычитания и размещения чисел. Решение магических квадратов увлекает школьников всех возрастов.
Задания на нахождение значений математических выражений.
Предлагается в той или иной форме математическое выражение, требуется найти его значение.
Эти задания имеют много вариантов. Можно предлагать числовые математические выражения и буквенные (выражение с переменной), при этом буквам придают числовые значения и находят числовое значение полученного выражения, например:
- найдите разность чисел 100 и 9.
- найдите значение выражения С – К, если С = 100, К = 9.
Выражения могут предлагаться в разной словесной форме:
- из 100 – 9; 100 минус 9
- уменьшаемое 100, вычитаемое 9, найдите разность
- найти разность чисел 100 и 9
- уменьшить 100 на 9 и т. д.
Эти формулировки использует не только учитель, но и ученики.
Выражения могут быть даны с ошибками, которые детям предстоит найти:
Задание 1. Найди ошибки в выражениях:
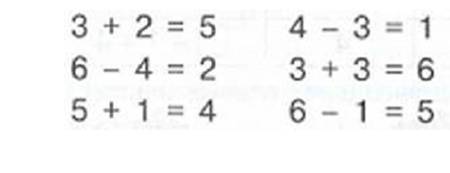
Выражения могут включать одно и более действий.
Могут быть со скобками или без скобок: (90 – 42) : 3, 90 – 42 : 3.
Выражения можно давать и в форме таблицы:
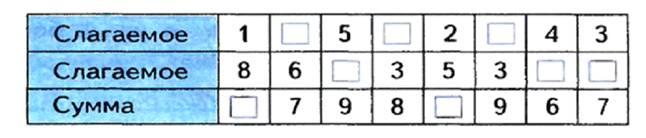
Так же такие задания в виде различных цепочек.
Реши цепочки:
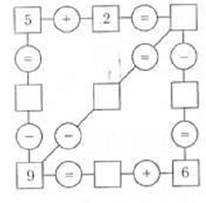
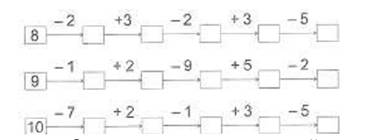
Основное значение заданий на нахождение значений выражений – выработать у учащихся твердые вычислительные навыки, а также они способствуют усвоению вопросов теории арифметических действий.
Комбинаторные задачи.
Комбинаторика - один из разделов современной математики. Комбинаторные задачи служат средством развития мышления детей, воспитания у них умения применять полученные знания в различных ситуациях посредством выработки навыков и повторения пройденного.
Умение выполнять разбиение множеств, составлять комбинации по определенным признакам и классифицировать лежит в основе разнообразных сфер человеческой деятельности.
Задание 1. При умножении двух однозначных чисел получилось число16
Чему были равны множители?
Найди всевозможные решения.
Рифмованные задачи помогают усваивать таблицы сложения и вычитания, умножения и деления.
Домино:
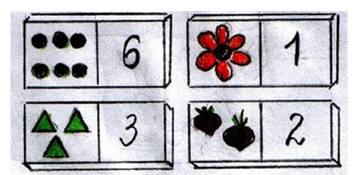
В 1 классе хорошо использовать домино. Работа с ним способствует формированию навыков табличного сложения и вычитания в пределах 10, а также знанию соответствующих случаев состава чисел.
Работа с "домино" проводится с постепенным повышением трудностей.
Числовой веер:
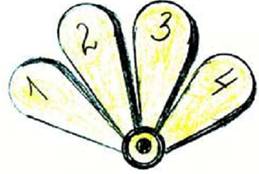
Хорошо использовать при проведении математического диктанта в 1- 2 классах. Сам же диктант активизирует внимание и мышление детей, способствует формированию вычислительных навыков.
Ромашка:
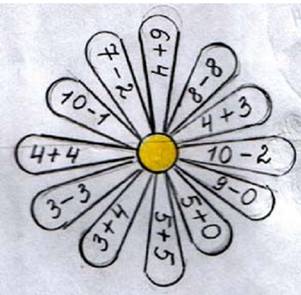
На лепестках цветка написаны числа от 1 до 10, а в середине знак (+, -) (x, : ) и прорезь, куда вставляются числа. Это пособие помогает проводить игру "Молчанка".
Таким образом, формирование вычислительных навыков - одна из главных задач, которая должна быть решена в ходе обучения детей в начальной школе.
Вычислительная культура является тем запасом знаний и умений, который находит повсеместное применение, является фундаментом изучения математики и других учебных дисциплин.
СПИСОК ЛИТЕРАТУРЫ
1. Актуальные проблемы методики обучения математике в начальных классах / Под ред. М. И.Моро, А. М. Пышкало. — М.: Педагогика, 1977. — 248 с.
2. Аргинская, И. И., Ивановская, Е. И Математика 2 класс. Часть 1. – С.:, Издательство «Корпорация Федоров», 2010 – 128 с.
3.Бадма – Гаряева, М. В. Развитие вычислительных навыков у учащихся 1 класса // Начальная школа – 1999 – №11 – с.21 – 23
4. Бантова, М. А., Бельтюкова, Г. В. Методика преподавания математики в нач. классах: Учеб. пособие для уч-ся школ. отд-ний пед. уч-щ / Под ред. М. А. Бантовой. - 3-е изд. - М.: Просвещение,19с.
5. Бантова, М. А. Система формирования вычислительных навыков // Начальная школа – 1993 - №11 – с. 38 – 43
6. Бахир, В. К. Развивающее обучение // Начальная школа – 1997 - №5 – с. 26 – 31
7. Давыдов, В. В. Проблемы развивающего обучения: опыт теоретического и экспериментального психологического исследования. –М.: Педагогика, 1986 – 239 с.
8. Давыдов, В. В. Содержание и строение учебной деятельности школьников. – М., 1978 – 321 с.
9. Давыдов, В. В. Теория развивающего обучения. – М.: ИНТОР, 1996 – 544 с.
10. Давыдов, В. В. Что такое учебная деятельность // Начальная школа – 1999 - №7 – с. 12 – 18
11. Зимняя, И. А. Педагогическая психология. – Ростов на Дону: Феникс, 1997 – 476 с.
12. Ильина, О. Н. Проблема формирования вычислительных навыков младших школьников в современных условиях // Интернет журнал СахГУ «Наука, образование, общество». – 20февраля. URL статьи: http://journal. *****.
13. Истомина, Н. Б. Методика обучения математике в начальных классах. – М., 1997
14. Клецкина, А. А. Организация вычислительной деятельности младших школьников в системе развивающего обучения // Автореферат диссертации на соискание ученой степени канд. пед. наук. — М., 2001. — 20 с.
15. Лавлинская, Е. Ю. Методика формирования вычислительного навыка по системе общего развития Занкова Л. В. – В.: Панорама, 2006.- с.176.
16. Мельникова, Н. А. Развитие вычислительной культуры учащихся // Математика в школе.- 2001.- №18.- С. 9-
17. Менчинская, Н. А. Моро М. И. Вопросы методики и психологии обучения арифметики в начальных классах.- М.: Просвещение, 196с.
18. Методика начального обучения математике: Учеб. пособие для студентов пед. ин-тов по спец-ти «Педагогика и методика начального обучения» // Под ред. Л. Н. Скаткина. – М.: просвещение, 197с.
10