Методы решения иррациональных уравнений. 10 класс.
Решение уравнений с помощью исследования ОДЗ.
Решим иррациональное уравнение стандартным методом, избавимся от иррациональности и затем выполнить проверку. Такой способ ведет к громоздким вычислениям, к решению рациональных уравнений четвертой, шестой степени, которые решить очень сложно. При решении некоторых уравнений знание ОДЗ уравнения и применение некоторых оценок позволяет найти все его корни или доказать, что их нет. Такой подход будет более рациональным.
Решите уравнение: 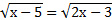
1 способ:
Рассмотрим область определения функций:
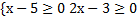
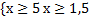
х-5=2х-3
х=-2, но -2 не входит в область определения функций, следовательно, решений нет.
Ответ: решений нет.
2 способ:
х-5=2х-3
х=-2
Проверка:
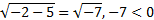
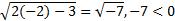
Значит, х=-2- посторонний корень
Ответ: решений нет
2. Решить уравнение:
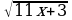 -
-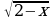 =
=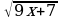 -
-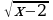
Решение:
- возведя в квадрат обе части уравнения, мы избавиться от иррациональности
11х+3-2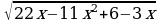 +2-х=9х+7-2
+2-х=9х+7-2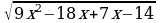 +х-2
+х-2
- приведем подобные слагаемые
10х+5-2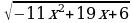 =10х+5-2
=10х+5-2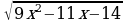
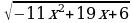 =
=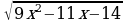 .
.
После возведения в квадрат обеих частей уравнения и приведя подобные слагаемые
мы получим стандартное квадратное уравнение
20х2-30х-20=0, сокращая уравнение, будет иметь вид:
2х2-3х-2=0, а его корни будут равны:
х1=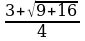 , х1=2 х2=
, х1=2 х2=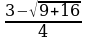 , х2=-0,5
, х2=-0,5
Полученные корни необходимо проверить, т.к. при возведении в квадрат, возможно
приобретение посторонних корней.
Проверка:
х=2, 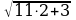 -
-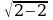 =5,
=5,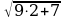 -
-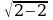 =5, 5=5
=5, 5=5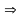 х=2 корень данного уравнения
х=2 корень данного уравнения
х=-0,5 ,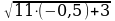 -
-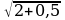 =
=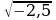 -
-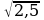
 х=-0,5-посторонний корень.
х=-0,5-посторонний корень.
Ответ: х=2
Однако, сравнив области определения функций у=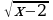 , (х-2
, (х-2 0, х
0, х 2) и у=
2) и у=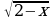 , (2-х
, (2-х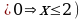 , приходим к выводу, что область определения исходного уравнения:
, приходим к выводу, что область определения исходного уравнения:
х=2.
Подставив х=2 в данное уравнение, приходим к выводу, что х=2 единственный
корень этого уравнения.
Ответ: х=2.
Очевидно, что решать данное уравнение вторым способом удобнее и быстрее чем первым.
Решение уравнений с помощью уединения радикала
3. Решить уравнение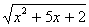 -
-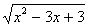 = 3.
= 3.
Решение.
Уединив первый радикал, получаем уравнение
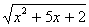 =
=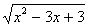 + 3, равносильное исходному
+ 3, равносильное исходному
.
Возводя обе части этого уравнения в квадрат, получаем уравнение
x2 + 5x + 2 = x2 - 3x + 3 + 6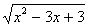 , равносильное уравнению
, равносильное уравнению
4x - 5 = 3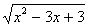 (*).
(*).
Это уравнение является следствием исходного уравнения. Возводя обе части уравнения в квадрат, приходим к уравнению
16x2 - 40x + 25 = 9(x2 - Зх + 3), или
7x2 - 13x - 2 = 0.
Это уравнение является следствием уравнения (*) (а значит, и исходного уравнения) и имеет корни. Первый корень x1 = 2 удовлетворяет исходному уравнению, а второй x2 =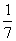 - не удовлетворяет.
- не удовлетворяет.
Ответ: x = 2.
Заметим, что если бы мы сразу, не уединив один из радикалов, возводили обе части исходного уравнения в квадрат нам бы пришлось выполнить довольно громоздкие преобразования.
Метода замены неизвестного (метод введения вспомогательной переменной).
4. Решить уравнение 2x2 - 6x +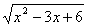 + 2 = 0.
+ 2 = 0.
Решение.
Введем вспомогательную переменную. Пусть y =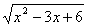 , где y
, где y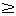 0, тогда получим уравнение 2y2 + y - 10 = 0;
0, тогда получим уравнение 2y2 + y - 10 = 0;
y1 = 2; y2 = -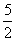 .
.
Второй корень не удовлетворяет условию y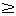 0.
0.
Возвращаемся к x:
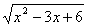 = 2;
= 2;
x2 - 3x + 6 = 4;
x2 -3x + 2 = 0;
x1 = 1; x2 = 2.
Проверкой устанавливаем, что оба корня являются корнями исходного уравнения.
Ответ: x1 = 1; x2 = 2.
Решение уравнений с использованием множества значений.
При решении некоторых уравнений нахождение множества значений существенно облегчает задачу решения уравнения.
.
5. Решить уравнение: 
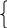 Решение: найдем область определения данного уравнения:
Решение: найдем область определения данного уравнения: 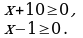
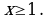
Оценим правую и левую части уравнений: 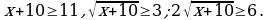 т.е.
т.е.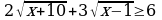 , а
, а 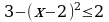 .
.
Левая часть уравнения больше правой части, значит, данное уравнение не имеет корней.
Ответ: нет корней.
Использование эквивалентности при решении уравнений.
При решении уравнений вида f(f(x)) = x применима теорема: «если у=f(х) – монотонно возрастающая функция, то уравнения f(x)=x и f(f(x))=x эквивалентны».
6. Решить уравнение 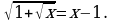
Решение: перенесем 1 влево, и уравнение будет иметь вид: 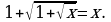 Рассмотрим функцию f(x)=1+
Рассмотрим функцию f(x)=1+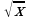 , эта функция монотонно возрастает. Имеем уравнение f(f(x))=x.
, эта функция монотонно возрастает. Имеем уравнение f(f(x))=x.
В соответствии с теоремой заменяем его эквивалентным уравнением f(x)=x или 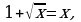
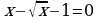 . Пусть
. Пусть 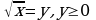 .
.
Имеем у2-у-1=0,
у1,2=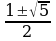 ; у1=
; у1=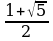 , у2=
, у2=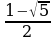 - не удовлетворяет условию
- не удовлетворяет условию 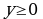 .
.
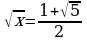 ,
, 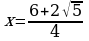 , х=
, х=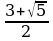 .
.
Ответ: х=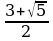 .
.
Литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.








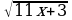 -
-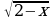 =
=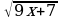 -
-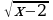
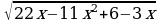 +2-х=9х+7-2
+2-х=9х+7-2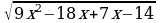 +х-2
+х-2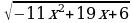 =10х+5-2
=10х+5-2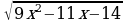
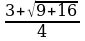 , х1=2 х2=
, х1=2 х2=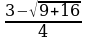 , х2=-0,5
, х2=-0,5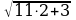 -
-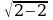 =5,
=5,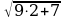 -
-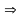 х=2 корень данного уравнения
х=2 корень данного уравнения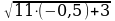 -
-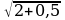 =
=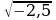 -
-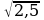
 0, х
0, х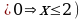 , приходим к выводу, что область определения исходного уравнения:
, приходим к выводу, что область определения исходного уравнения:
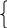 Решение: найдем область определения данного уравнения:
Решение: найдем область определения данного уравнения: 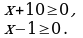
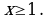
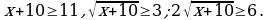 т.е.
т.е.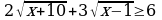 , а
, а 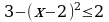 .
.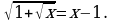
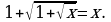 Рассмотрим функцию f(x)=1+
Рассмотрим функцию f(x)=1+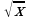 , эта функция монотонно возрастает. Имеем уравнение f(f(x))=x.
, эта функция монотонно возрастает. Имеем уравнение f(f(x))=x.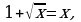
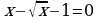 . Пусть
. Пусть 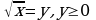 .
.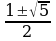 ; у1=
; у1=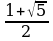 , у2=
, у2=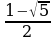 - не удовлетворяет условию
- не удовлетворяет условию 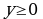 .
.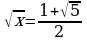 ,
, 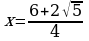 , х=
, х=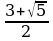 .
.









