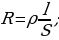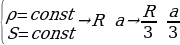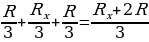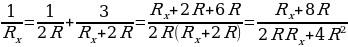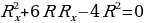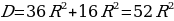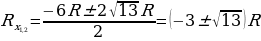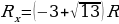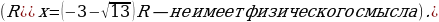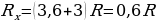Муниципальное бюджетное образовательное учреждение
«Средняя общеобразовательная школа № 39» г. Чебоксары
Методы решения задач для расчета
бесконечных электрических цепей
Филиппова Н. А. – учитель физики
МБОУ «СОШ № 39» г. Чебоксары.
Чебоксары 2022
Содержание
Введение……….........................................................................................................2
Примеры решения задач…………………………………………………………..7
-
Задача 1…………………………………………………………………………7
-
Задача 2…………………………………………………………………………8
-
Задача 3………………………………………………………………………..10
-
Задача 4………………………………………………………………………..10
-
Задача 5………………………………………………………………………..11
-
Задача 6………………………………………………………………………..12
-
Задача 7………………………………………………………………………..14
Заключение……………………………………………………………………….16
Список использованной литературы…………………………………………...17
Введение
Решение задач - неотъемлемая часть обучения физике, поскольку в процессе решения задач происходит формирование и обогащение физических понятий, развивается физическое мышление учащихся и совершенствуется их навыки применения знаний на практике.
В ходе решения задач могут быть поставлены и успешно реализованы следующие дидактические цели:
-
Выдвижение проблемы и создание проблемной ситуации;
-
Обобщение новых сведений;
-
Формирование практических умений и навыков;
-
Проверка глубины и прочности знаний;
-
Закрепление, обобщение и повторение материала;
-
Реализация принципа политехнизма;
-
Развитие творческих способностей учащихся.
Наряду с этим при решении задач у школьников воспитываются трудолюбие, пытливость ума, смекалка, самостоятельность в суждениях, интерес к учению, воля и характер, упорство в достижении поставленной цели. Для реализации перечисленных целей особенно удобно использовать нетрадиционные задачи.
К таким, нестандартным задачам по расчету электрических цепей постоянного тока можно отнести задачи, схемы которых:
1) содержат большое число элементов – резисторов или конденсаторов;
2) симметричны;
3) состоят из сложных смешанных соединений элементов.
Нужно уметь пользоваться методами, позволяющими быстро найти сопротивления.
В данной работе рассматриваются методы решения задач для расчета бесконечных электрических цепей.
Примеры решения задач
-
Ц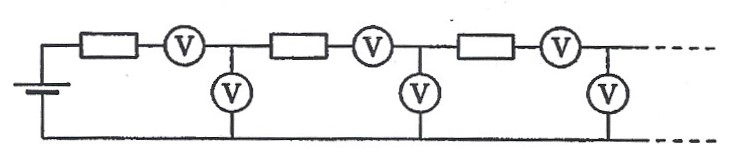
епь содержит огромное количество звеньев, каждое звено состоит из резистора и двух вольтметров. Все вольтметры в цепи одинаковы, сопротивления всех резисторов цепи равны между собой. Цепь подключают к батарейке, при этом первые два вольтметра показывают напряжения 6 В и 4 В. Найти показания второй пары вольтметров. Найти сумму показаний всех вольтметров цепи.
Решение:
Обозначим сопротивление бесконечной цепочки звеньев Х, сопротивления резистора и вольтметра r и R соответственно. Сопротивление такой цепочки не должно измениться при д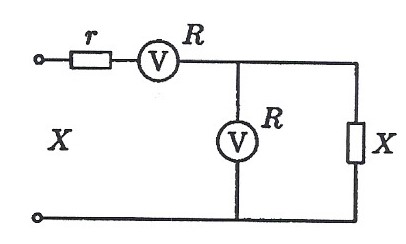 обавлении или отбрасывании одного звена (резистор и два вольтметра). Следовательно, можно считать, что параллельно второму вольтметру подключен резистор с сопротивлением Х, и мы можем записать соотношение для упростившейся схемы:
обавлении или отбрасывании одного звена (резистор и два вольтметра). Следовательно, можно считать, что параллельно второму вольтметру подключен резистор с сопротивлением Х, и мы можем записать соотношение для упростившейся схемы:
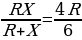 (вспoмним показания вольтметров!). Отсюда Х = 2R. Теперь легко найти величину r: r + R + 2R/3 = Х =2R; r = R/3. Для первого звена напряжение на резисторе r получается 6/3 = 2 (В), а напряжение батарейки составляет 12 В. Второе звено цепи (и бесконечная цепочка, начиная со второго звена) подключены к напряжению 4 В, показания вольтметров этого звена в 3 раза меньше, чем первого звена, и т. д. Тoгда понятно, что показания вольтметров составят 2 В и 4/3 В. Легко найти и сумму показаний вольтметров в этой цепи - первое звено дает 10 В, второе — в 3 раза меньше и т. д. Пользуясь формулой для нахождения суммы бесконечной геометрической прогрессии, получим сумму:
(вспoмним показания вольтметров!). Отсюда Х = 2R. Теперь легко найти величину r: r + R + 2R/3 = Х =2R; r = R/3. Для первого звена напряжение на резисторе r получается 6/3 = 2 (В), а напряжение батарейки составляет 12 В. Второе звено цепи (и бесконечная цепочка, начиная со второго звена) подключены к напряжению 4 В, показания вольтметров этого звена в 3 раза меньше, чем первого звена, и т. д. Тoгда понятно, что показания вольтметров составят 2 В и 4/3 В. Легко найти и сумму показаний вольтметров в этой цепи - первое звено дает 10 В, второе — в 3 раза меньше и т. д. Пользуясь формулой для нахождения суммы бесконечной геометрической прогрессии, получим сумму:
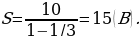
-
Из множества одинаковых вольтметров собрана обычная «бесконечная» цепь, подключенная к батарейке. Первый из вольтметров показывает больше всех - его стрелка отклоняется почти ни всю шкалу. Погрешность приборов составляет 1%. Сколько приборов показывают напряжение превышающие порог погрешности?
Вот так выглядит обычная «бесконечная» цепь из вольтметров:
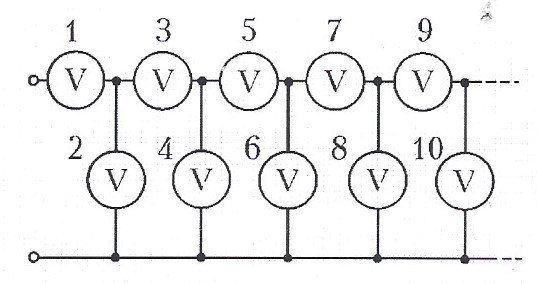
Решение:
Если сопротивление одного вольтметра равно R, то сопротивление Z всей цепочки вольтметров можно найти из уравнения
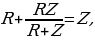 откуда
откуда
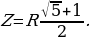
Если ЭДС батарейки равна Ε, то первый вольтметр покажет значение
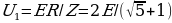 , второй вольтметр покажет
, второй вольтметр покажет 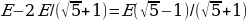 , третий покажет
, третий покажет 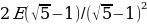 , четвертый —
, четвертый — 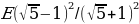 и т.д. В результате все нечетные вольтметры— их n — показывают значения
и т.д. В результате все нечетные вольтметры— их n — показывают значения
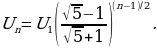
Все четные вольтметры— их k— показывают значения
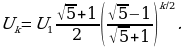
Чтобы нечетный вольтметр показывал значение меньше, чем погрешность прибора, его номер n должен быть таким, чтобы выполнялось неравенство
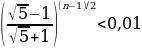
Отсюда находим n = 11. Чтобы четный вольтметр показывал значение меньше, чем погрешность прибора, нужно, чтобы
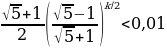
Отсюда получаем k = 12.
Следовательно, всего 12 приборов показывают напряжения большие, чем их погрешность.
-
Найдите эквивалентное сопротивление бесконечной цепочки, которая состоит из одинаковых резисторов сопротивлением R каждый.
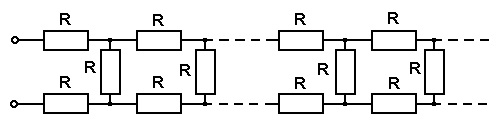
Решение (типовое, алгоритм). Для нахождения эквивалентного сопротивления цепи необходимо выделить общую секцию, которая бесконечно повторяется. Вполне очевидно, что если отделить ее от цепи, то общее сопротивление этой цепи не изменится, т.к. число элементов (секций) бесконечно. В силу вышесказанного, выделив повторяющуюся секцию в цепи и заменив сопротивление остальной цепи искомым сопротивлением R, получим эквивалентную схему. Найдем сопротивление цепи, предварительно записав выражение для 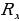 , через
, через 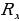 . Опуская промежуточные выкладки, получим:
. Опуская промежуточные выкладки, получим:
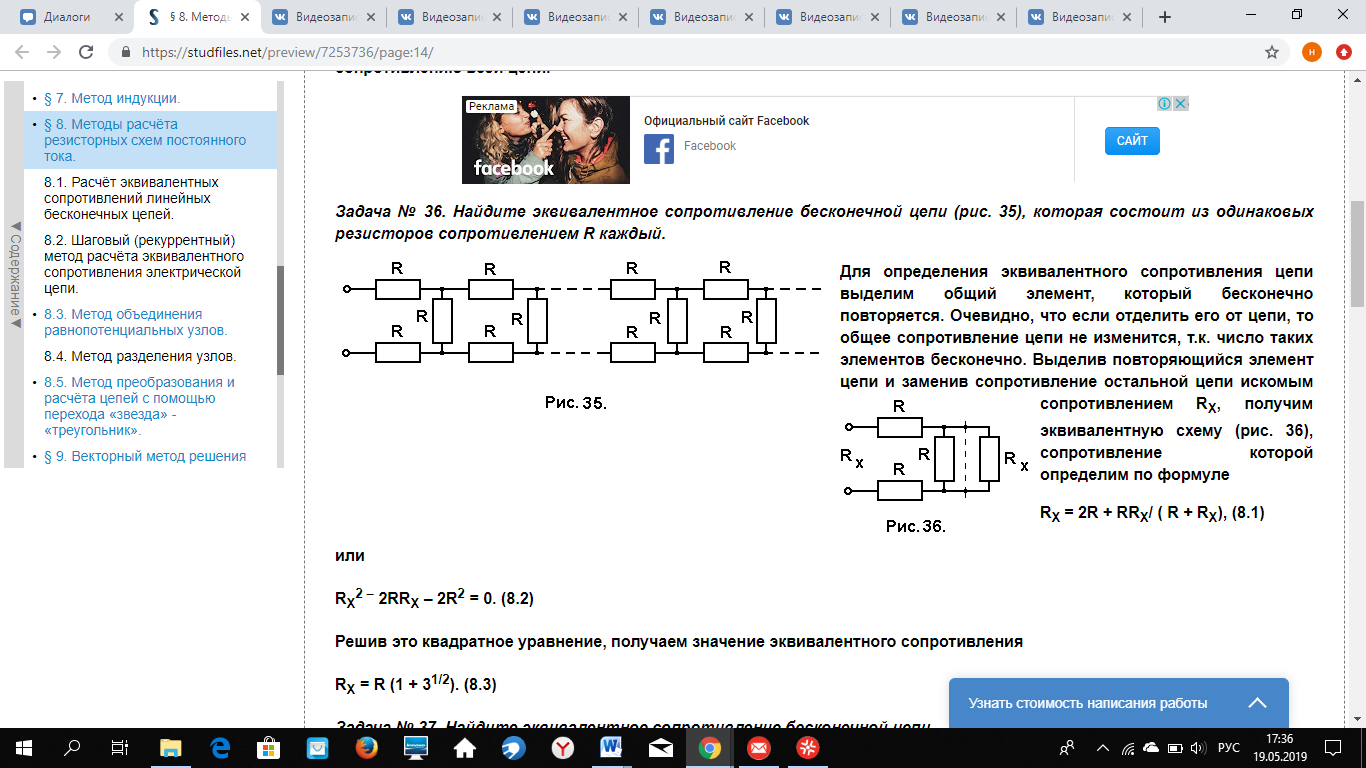
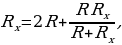
или 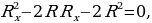 откуда получим ответ:
откуда получим ответ:
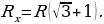
Рассмотрим еще одну подобную задачу.
-
Найдите эквивалентное сопротивление между точками А и В бесконечной цепочки, которая состоит из одинаковых резисторов сопротивлением R каждый.

Решение. Эквивалентное сопротивление цепи равно сопротивлению двух одинаковых и параллельно соединенных резисторов, сопротивления которых равны (см. решение задачи 3 ):
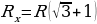 —справа и
—справа и 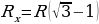 —слева
—слева
Тогда после простых расчетов легко получить ответ:
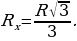
-
Найдите эквивалентное сопротивление между точками А и В бесконечной цепочки, которая состоит из одинаковых проволочных резисторов сопротивлением R каждый.
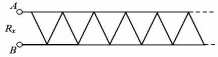
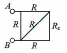 Решение. Эквивалентная схема представлена на рисунке. Повторяющаяся секция состоит из четырех резисторов. Полное сопротивление цепи находим, полагая
Решение. Эквивалентная схема представлена на рисунке. Повторяющаяся секция состоит из четырех резисторов. Полное сопротивление цепи находим, полагая 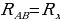 . Опуская промежуточные выкладки, получим
. Опуская промежуточные выкладки, получим
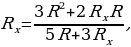
или
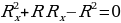
Откуда следует, что
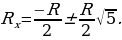
Второй корень уравнения отрицательный и имеет смысла. Окончательный результат:
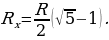
Рассмотрим более трудную задачу, решение которой предполагает предварительное использование метода исключения пассивных элементов цепи.
-
Найти эквивалентное сопротивление между точками А и В бесконечной цепочки, которая состоит из одинаковых проволочных резисторов с сопротивлением R каждый. Решение. Чтобы найти эквивалентное сопротивление цепи, необходимо сначала выделить общую секцию, которая бесконечно повторяется. Понятно, что если отдалить её от цепи, то общее сопротивление этой цепи не изменится. Выделить повторяющуюся секцию в рассматриваемой цепи можно, но заменить сопротивление остальной части искомым сопротивлением 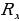 нельзя, т.к. оставшаяся часть имеет четыре соединительных провода.
нельзя, т.к. оставшаяся часть имеет четыре соединительных провода.
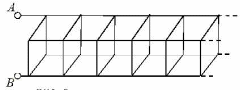
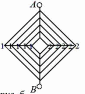
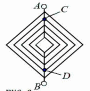

Если посмотрим на каркас слева, то получим изображение цепи в перспективе, приведенное на рисунке. Из симметрии этого рисунка видно, что потенциалы точек, обозначенных цифрой 1, одинаковы и равны потенциалам точек, обозначенных цифрой 2.
Исключим из рассмотрения пассивные резисторы, соединяющие точки 1 и 2. Между точками C и D находится фигура, эквивалентное сопротивление которой равна искомому, т.к. цепь бесконечна.
Обозначим искомое сопротивление через 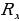 и получим (аналогично решению задачи 3)
и получим (аналогично решению задачи 3)
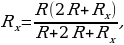
или 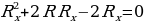 , откуда следует, что
, откуда следует, что
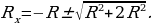
Второй корень уравнения отрицательный и не имеет смысла. Окончательный результат:
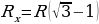
-
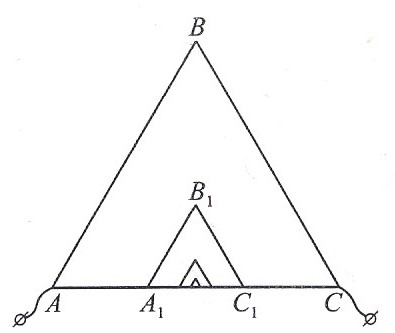 Из однородной проволоки изготовлен равносторонний треугольник АВС, сторона которого равна а. К точкам
Из однородной проволоки изготовлен равносторонний треугольник АВС, сторона которого равна а. К точкам 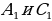 , делящим сторону AC на три равные части, прикреплены ещё два куска проволоки — вместе с отрезком
, делящим сторону AC на три равные части, прикреплены ещё два куска проволоки — вместе с отрезком 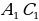 они образуют равносторонний треугольник
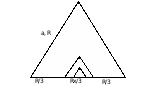
они образуют равносторонний треугольник 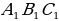 со стороной а/3. Внутри этого треугольника сделан ещё один (в три раза меньший) и т.д. Найдите сопротивление всей конструкции, если число треугольников очень велико. Сопротивление куска проволоки длины a равно r.
со стороной а/3. Внутри этого треугольника сделан ещё один (в три раза меньший) и т.д. Найдите сопротивление всей конструкции, если число треугольников очень велико. Сопротивление куска проволоки длины a равно r.
Решение: 1)
1)
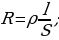
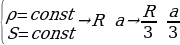
2)
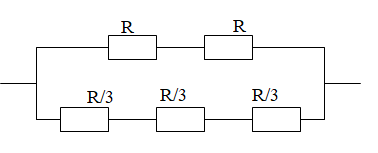
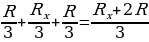
-
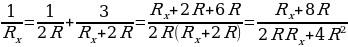
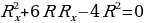
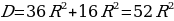
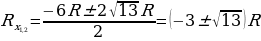
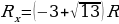
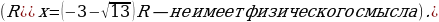
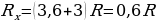
Заключение
В данной работе рассмотрены основные методы решения задач для расчета бесконечных электрических цепей, которые описаны и представлены на примерах разных задач.
Задача – это проблема, для разрешения которой ученику потребуются логические рассуждения и выводы. Строящиеся на основе законов и методов физики. Таким образом, с помощью задач происходит активизация целенаправленного мышления учащихся.
При решении нестандартных задач формируется логическое мышление, развивается интуиция, систематизируются знания, расширяется общеобразовательный кругозор, накапливается полезный опыт. Можно овладеть основными методами решения задач, составляющих важную часть многих эвристических алгоритмов, учиться рационально, планировать поиск решения задачи, выполнять полезные преобразования условия задачи.
Список использованной литературы
-
Петросян, В. Г. Методы расчета резисторных схем постоянного тока.
10-11-й классы. Углубленный курс / В. Г. Петросян, Л. В. Долгополова, И. В. Лихицкая // Физика. —2002. —№18. —С. 5– 7.
-
Перунова, М. Н. Расчет электрических цепей: практикум/
М. Н. Перунова. – Оренбург: ОГУ, 2014. – 121 с.
-
Варламов, С. Д. Задачник Кванта. Решения задач Ф2196-2204 // Квант. — 2011. — № 1. — С. 21–25.
-
Александров, Д. А. Задачник Кванта. Решения задач Ф1613-1622// Квант. — 1998. — № 1. — С. 26.







 обавлении или отбрасывании одного звена (резистор и два вольтметра). Следовательно, можно считать, что параллельно второму вольтметру подключен резистор с сопротивлением Х, и мы можем записать соотношение для упростившейся схемы:
обавлении или отбрасывании одного звена (резистор и два вольтметра). Следовательно, можно считать, что параллельно второму вольтметру подключен резистор с сопротивлением Х, и мы можем записать соотношение для упростившейся схемы: 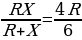 (вспoмним показания вольтметров!). Отсюда Х = 2R. Теперь легко найти величину r: r + R + 2R/3 = Х =2R; r = R/3. Для первого звена напряжение на резисторе r получается 6/3 = 2 (В), а напряжение батарейки составляет 12 В. Второе звено цепи (и бесконечная цепочка, начиная со второго звена) подключены к напряжению 4 В, показания вольтметров этого звена в 3 раза меньше, чем первого звена, и т. д. Тoгда понятно, что показания вольтметров составят 2 В и 4/3 В. Легко найти и сумму показаний вольтметров в этой цепи - первое звено дает 10 В, второе — в 3 раза меньше и т. д. Пользуясь формулой для нахождения суммы бесконечной геометрической прогрессии, получим сумму:
(вспoмним показания вольтметров!). Отсюда Х = 2R. Теперь легко найти величину r: r + R + 2R/3 = Х =2R; r = R/3. Для первого звена напряжение на резисторе r получается 6/3 = 2 (В), а напряжение батарейки составляет 12 В. Второе звено цепи (и бесконечная цепочка, начиная со второго звена) подключены к напряжению 4 В, показания вольтметров этого звена в 3 раза меньше, чем первого звена, и т. д. Тoгда понятно, что показания вольтметров составят 2 В и 4/3 В. Легко найти и сумму показаний вольтметров в этой цепи - первое звено дает 10 В, второе — в 3 раза меньше и т. д. Пользуясь формулой для нахождения суммы бесконечной геометрической прогрессии, получим сумму: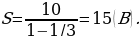

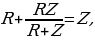 откуда
откуда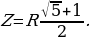
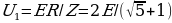 , второй вольтметр покажет
, второй вольтметр покажет 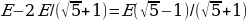 , третий покажет
, третий покажет 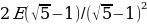 , четвертый —
, четвертый — 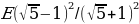 и т.д. В результате все нечетные вольтметры— их n — показывают значения
и т.д. В результате все нечетные вольтметры— их n — показывают значения 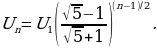
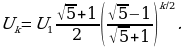
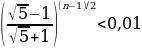
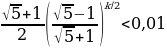

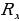 , через
, через 
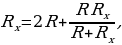
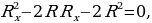 откуда получим ответ:
откуда получим ответ: 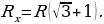

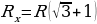 —справа и
—справа и 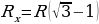 —слева
—слева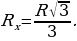

 Решение. Эквивалентная схема представлена на рисунке. Повторяющаяся секция состоит из четырех резисторов. Полное сопротивление цепи находим, полагая
Решение. Эквивалентная схема представлена на рисунке. Повторяющаяся секция состоит из четырех резисторов. Полное сопротивление цепи находим, полагая 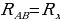 . Опуская промежуточные выкладки, получим
. Опуская промежуточные выкладки, получим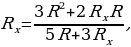
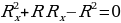
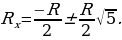
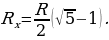




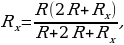
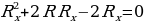 , откуда следует, что
, откуда следует, что 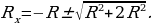
 Из однородной проволоки изготовлен равносторонний треугольник АВС, сторона которого равна а. К точкам
Из однородной проволоки изготовлен равносторонний треугольник АВС, сторона которого равна а. К точкам 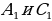 , делящим сторону AC на три равные части, прикреплены ещё два куска проволоки — вместе с отрезком
, делящим сторону AC на три равные части, прикреплены ещё два куска проволоки — вместе с отрезком 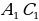 они образуют равносторонний треугольник
они образуют равносторонний треугольник 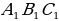 со стороной а/3. Внутри этого треугольника сделан ещё один (в три раза меньший) и т.д. Найдите сопротивление всей конструкции, если число треугольников очень велико. Сопротивление куска проволоки длины a равно r.
со стороной а/3. Внутри этого треугольника сделан ещё один (в три раза меньший) и т.д. Найдите сопротивление всей конструкции, если число треугольников очень велико. Сопротивление куска проволоки длины a равно r.  1)
1)