Многогранники вокруг нас. Султанова Светлана

Многогранники вокруг нас

Выполнила: ученица 11 А класса МБОУ СШ №75 города Ульяновска Султанова Светлана

Учитель: Малкова Елена Михайловна

Цели работы:

• Познакомиться с многогранниками Показать связь геометрии и природы Познакомиться с примерами применения многогранников в архитектуре и искусстве. Показать значение многогранников в истории .
• Познакомиться с многогранниками
• Показать связь геометрии и природы
• Познакомиться с примерами применения многогранников в архитектуре и искусстве.
• Показать значение многогранников в истории .

Введение

• В повседневной жизни мы часто встречаемся с красивыми, достаточно интересными фигурами, которые являются многогранниками.
• В геометрии изучаются разные виды многогранников: пирамиды, призмы, правильные многогранники. Ни одно геометрическое тело не обладает такой красотой, как правильные многогранники.
• Многогранники имеют красивые формы, например, правильные, полуправильные и звездчатые многогранники. Они обладают богатой историей, которая связана с именами таких ученых, как Пифагор, Евклид, Архимед.

История многогранников

• Первые упоминания о многогранниках известны еще за три тысячи лет до нашей эры в Египте и Вавилоне. Достаточно вспомнить знаменитые египетские пирамиды и самую известную из них – пирамиду Хеопса. Это правильная пирамида, в основании которой квадрат со стороной 233 м и высота которой достигает 146,5 м. Не случайно говорят, что пирамида Хеопса – немой трактат по геометрии.
• История правильных многогранников уходит в глубокую древность. Начиная с 7 века до нашей эры в Древней Греции создаются философские школы. Большое значение в этих школах приобретают рассуждения, с помощью которых удалось получать новые геометрические свойства.
• Одной из первых и самых известных школ была Пифагорейская, названная в честь своего основателя Пифагора. Отличительным знаком пифагорейцев была пентаграмма, на языке математики- это правильный невыпуклый или звездчатый пятиугольник. Пентаграмме присваивалось способность защищать человека от злых духов.

• Многогранник - часть пространства, ограниченная совокупностью конечного числа плоских многоугольников, соединенных таким образом, что каждая сторона любого многоугольника является стороной ровно одного другого многоугольника (называемого смежным), причем вокруг каждой вершины существует ровно один цикл многоугольников. 

• Пифагорейцы полагали, что материя состоит из четырех основных элементов: огня, земли, воздуха и воды. Существование пяти правильных многогранников они относили к строению материи и Вселенной. Согласно этому мнению, атомы основных элементов должны иметь форму различных тел:

земля

гексаэдр

вселенная

(куб)

додекаэдр

История многогранников

История многогранников

• Позже учение пифагорейцев о правильных многогранниках изложил в своих трудах другой древнегреческий ученый, философ - идеалист Платон. С тех пор правильные многогранники стали называться платоновыми телами.
• Открытие тринадцати полуправильных выпуклых многогранников приписывается Архимеду, впервые перечислившего их в недошедшей до нас работе. Ссылки на эту работу имеются в трудах математика Паппа.

• Многогранник называется правильным , если все его грани – равные правильные многоугольники и в каждой вершине сходится одно и то же число граней
• Существует всего пять таких многогранников.
• Сумма плоских углов при каждой вершине многогранного угла должна быть меньше 360 °.
• Величина угла правильного многоугольника находится по формуле
• n- число сторон(углов) правильного многоугольника; наименьшее количество плоских углов при вершине многогранника – 3.

Правильные многогранники

• Тетраэдр -четырехгранник, все грани которого треугольники, т.е. треугольная пирамида; правильный тетраэдр ограничен четырьмя равносторонними треугольниками.

Правильные многогранники

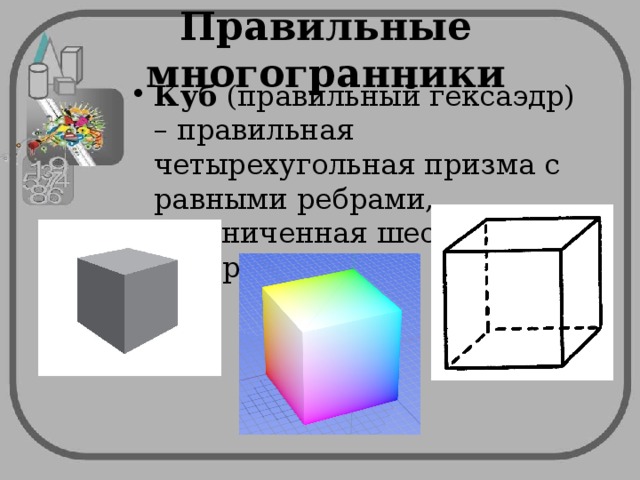
• Куб (правильный гексаэдр) – правильная четырехугольная призма с равными ребрами, ограниченная шестью квадратами.

Правильные многогранники

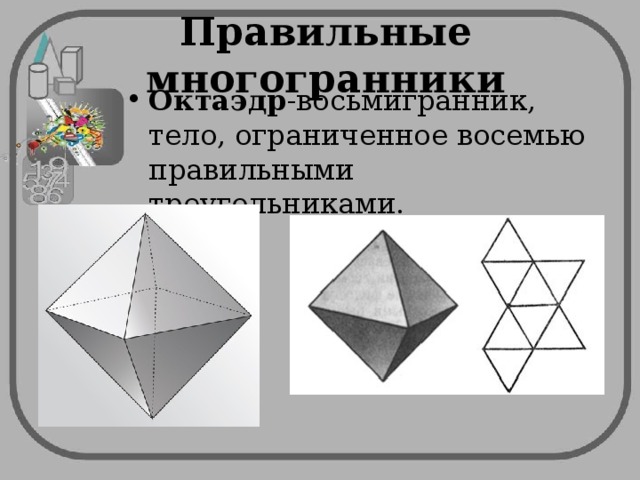
• Октаэдр -восьмигранник, тело, ограниченное восемью правильными треугольниками.

Правильные многогранники

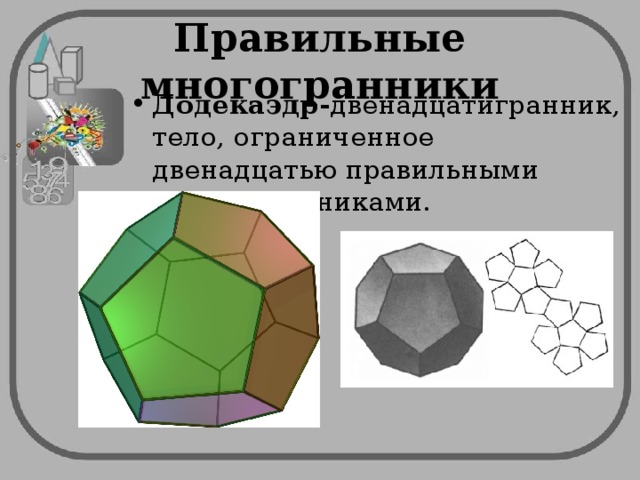
• Додекаэдр- двенадцатигранник, тело, ограниченное двенадцатью правильными многоугольниками.

Правильные многогранники

• Икосаэдр- двадцатигранник, тело, ограниченное двадцатью равносторонними треугольниками.

Теорема Эйлера

• Пусть В - число вершин выпуклого многогранника, Р - число его рёбер и Г - число граней. Тогда верно равенство В-Р+Г=2. Число = В-Р+Г называется эйлеровой характеристикой многогранника. Согласно теореме Эйлера, для выпуклого многогранника эта характеристика равна 2. То что эйлерова характеристика равна 2 для некоторых знакомых нам многогранников, видно из таблицы.

Многогранник

Число вершин

Тетраэдр

Куб

Число ребер

4

Число граней

8

6

Октаэдр

4

6

12

Додекаэдр

В-Р+Г

20

6

12

2

Икосаэдр

8

2

N- угольная пирамида

30

12

12

N+1

N -угольная призма

2

30

30

2N

2

2N

N+1

2

3N

2

N+2

2

Полуправильные многогранники (тела Архимеда)

• Полуправильным называется выпуклый многогранник, гранями которого являются правильные многоугольники (возможно с разным числом сторон), причём в каждой вершине сходится одинаковое число граней.

Многогранники в архитектуре

• Великая пирамида в Гизе – эта грандиозная Египетская пирамида является древнейшим из Семи чудес древности. Кроме того, это единственное из чудес, сохранившееся до наших дней. Во времена своего создания Великая пирамида была самым высоким сооружением в мире. И удерживала она этот рекорд, по всей видимости, почти 4000 лет.

Многогранники в архитектуре

• Мечеть Кул-Шариф Одна из главных мусульманских мечетей республики Татарстан и Казани. Расположена на территории Казанского кремля. Архитектура этой мечети представляет собой сочетание различных многогранников.

Многогранники в архитектуре

• Храм Артемиды Эфесской Храм достигал 109 метров в длину, 50 - в ширину. 127 двадцатиметровых колонн окружали его в два ряда, причем часть колонн были резными и барельефы на них выполнял знаменитый скульптор Скопас. Основание крыши – мраморная плита.

Многогранники в архитектуре

• Александрийский маяк В 285 году до н.э.на острове Фарос архитектор Сострат Книдский приступил к строительству маяка. Маяк строился пять лет и получился в виде трехэтажной башни высотой 120 метров. В основании он был квадратом со стороной тридцать метров, первый 60-метровый этаж башни был сложен из каменных плит и поддерживал 40-метровую восьмигранную башню, облицованную белым мрамором. На третьем этаже, в круглой, обнесенной колоннами башне, вечно горел громадный костер, отражавшийся сложной системой зеркал.

Многогранники в архитектуре

• Стеклянная пирамида Лувра Трехгранная стеклянная пирамида в Лувре в Париже - интересная и необычная достопримечательность, которая служит главным входом в Лувр. Стеклянная пирамида, состоит из 603 ромбовидных и 70 треугольных стеклянных сегментов.

Многогранники в архитектуре

Исторический музей

Казанская церковь в Москве

Многогранники в архитектуре

• Памятник правильным многогранникам в Германии

Многогранники в искусстве

• В эпоху Возрождения большой интерес к формам правильных многогранников проявили скульпторы, архитекторы, художники. Леонардо да Винчи (1452 -1519) увлекался теорией многогранников и часто изображал их на своих полотнах. Он проиллюстрировал правильными и полуправильными многогранниками книгу монаха Луки Пачоли ''О божественной пропорции.''

Многогранники в искусстве

• Тайная вечеря - Сальвадор Дали Автор намеренно переносит действие картины в современное пространство. Над столом стеклянный купол, за которым открывается безжизненный пейзаж: море, скальные острова, многоцветное небо. Среди сидящих за каменным столом, лишь центральная фигура Христа выглядит живой. Ученики, почтительно склонив головы, слушают Учителя. Над столом витает полупрозрачный торс с распростертыми руками. С одной стороны, он как Дух Святой объединяет всех участников вечери, с другой, выступает неким предвестием скорого распятия. Геометрически точна перспектива картины. Идеально точно размещены половинки хлеба. Ученики за столом размещены по законам идеальной центральной симметрии.

Кристаллы

Многогранники в биологии

• Пчёлы строили свои шестиугольные соты задолго до появления человека.

Многогранники в биологии

• Геометрические свойства икосаэдра позволяют экономить генетическую информацию.

Многогранники в биологии

• Икосаэдр оказался в центре внимания биологов в их спорах относительно формы вирусов.
• Скелет одноклеточного организма феодарии (Circogonia icosahedra) по форме напоминает икосаэдр.Большинство феодарий живут на морской глубине и служат добычей коралловых рыбок. Но простейшее животное защищает себя двенадцатью иглами, выходящими из 12 вершин скелета. Он больше похоже на звёздчатый многогранник.

Используемые ресурсы:

• Энциклопедия для детей. Т. 11. Математика. – М: Аванта плюс, 2002.
• Энциклопедия для детей. Я познаю мир.Математика. – М: Издательство АСТ, 1999.
• Рыбников К.А. История математики: Учебник. – М.: Изд-во МГУ, 1994. – 495 с
• Мир многогранников: http://www.sch57.msk.ru:8101/collect/smogl.htm
• История математики:http://mschool.kubsu.ru/
• Статьи по математике:http://dondublon.chat.ru/math.htm
• Популярная математика:http://www.uic.ssu.samara.ru/~nauka/index.htm