Многоугольники. Четырехугольники.

Многоугольники

К учебнику Л.С.Атанасяна

Геометрия 7 - 9, Глава V, пп. 40-42, 8 класс

Автор: Софронова Наталия Андреевна,

учитель математики высшей категории

МОУ «Упшинская основная общеобразовательная школа»

Оршанского района Республики Марий Эл

Ломаная

B

Фигура на рисунке составлена из отрезков АВ, ВС, CD, DE, EF, FS, ST, TR.

Отрезки АВ и ВС, ВС и CD и т.п. называются смежными .

Смежные отрезки не лежат на одной прямой.

Данная фигура называется ломаной .

C

D

А

E

T

S

F

R

Отрезки АВ, ВС, CD, DE, EF, FS, ST, TR называются звеньями ломаной.

Концы отрезков - точки А, В, C, D, E, F, S, T и R называются вершинами ломаной.

Точки А и R называются концами ломаной.

Сумма длин всех звеньев называется длиной ломаной.

Ломаная

B

B

C

C

D

D

А

А

(R)

E

E

T

T

S

S

R

F

F

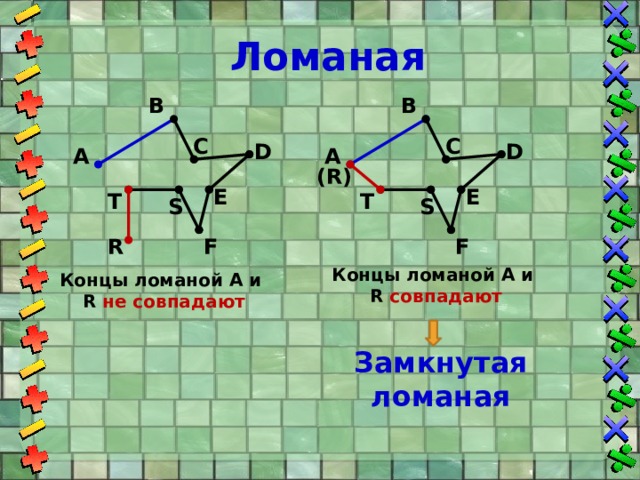
Концы ломаной А и R совпадают

Концы ломаной А и R не совпадают

Замкнутая ломаная

Многоугольник

T

B

B

C

C

D

D

А

S

E

E

S

T

А

F

F

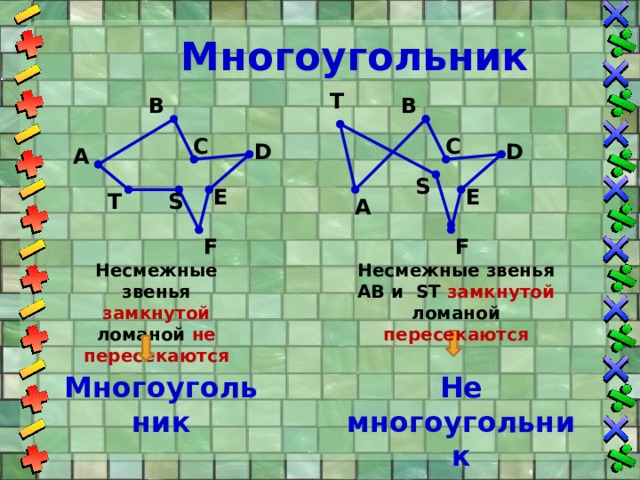
Несмежные звенья AB и ST замкнутой ломаной пересекаются

Несмежные звенья замкнутой ломаной не пересекаются

Многоугольник

Не многоугольник

Многоугольник

B

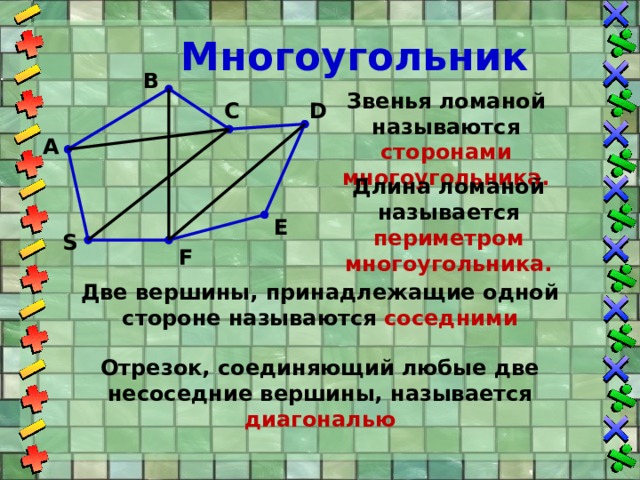
Звенья ломаной называются сторонами многоугольника.

C

D

А

Длина ломаной называется периметром многоугольника.

E

S

F

Две вершины, принадлежащие одной стороне называются соседними

Отрезок, соединяющий любые две несоседние вершины, называется диагональю

а)

б)

в)

г)

е)

д)

з)

е)

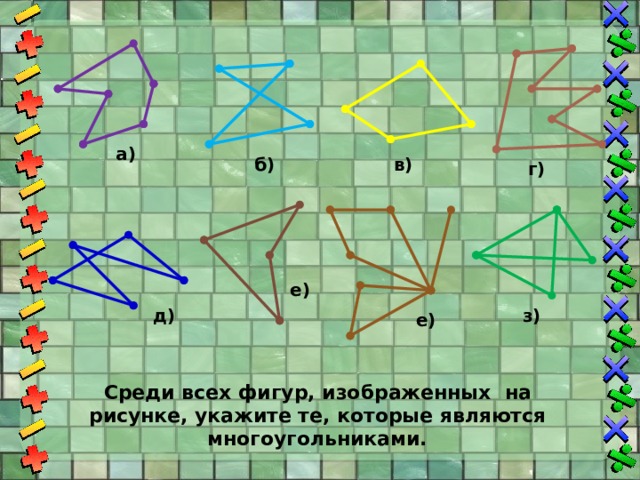
Среди всех фигур, изображенных на рисунке, укажите те, которые являются многоугольниками.

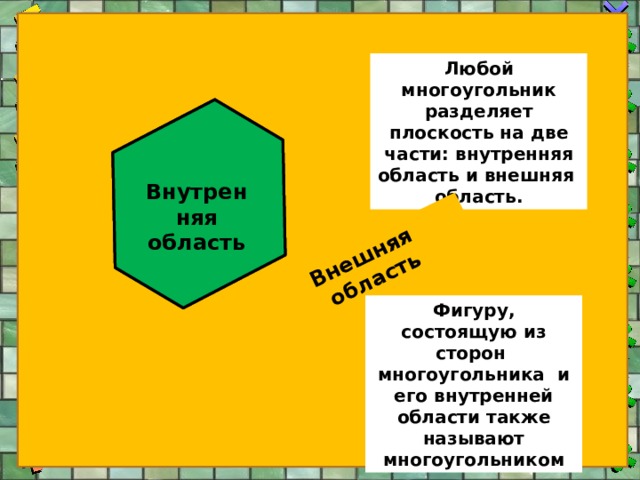
Внешняя область

Любой многоугольник разделяет плоскость на две части: внутренняя область и внешняя область.

Внутренняя область

Фигуру, состоящую из сторон многоугольника и его внутренней области также называют многоугольником

Многоугольник с n вершинами называется n-угольником

n = 3

треугольник

n = 6

шестиугольник

n = 4

n = 5

четырехугольник

пятиугольник

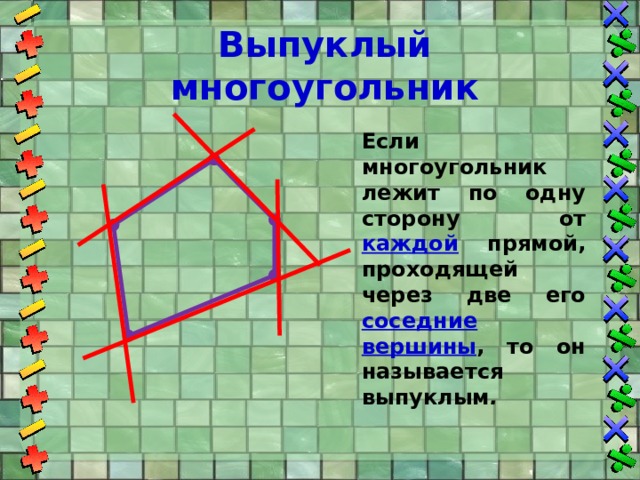
Выпуклый многоугольник

Если многоугольник лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины , то он называется выпуклым .

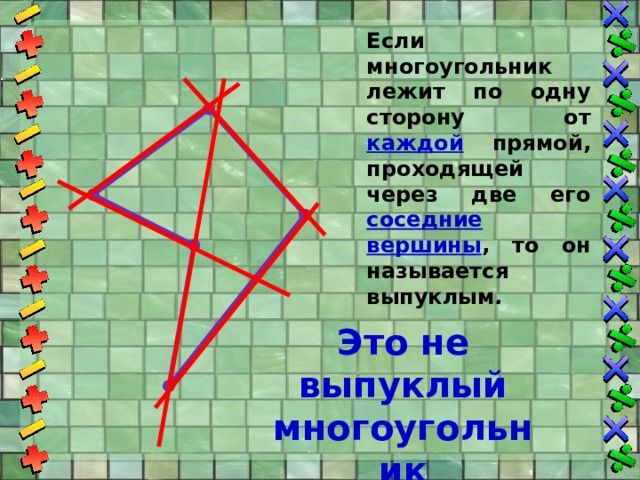
Если многоугольник лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины , то он называется выпуклым .

Это не выпуклый многоугольник

а)

г)

б)

в)

д)

з)

е)

е)

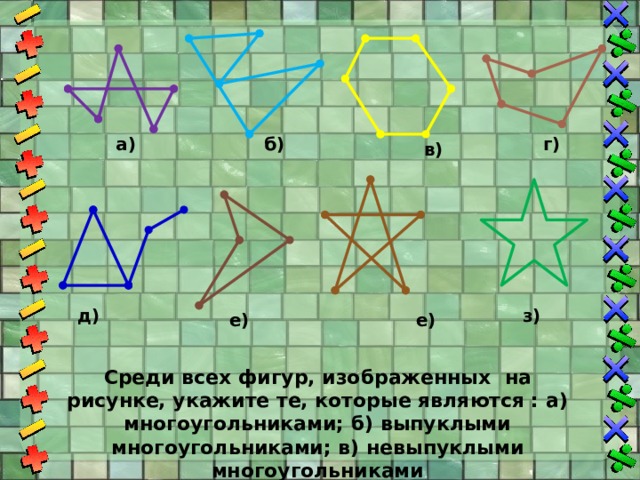
Среди всех фигур, изображенных на рисунке, укажите те, которые являются : а) многоугольниками; б) выпуклыми многоугольниками; в) невыпуклыми многоугольниками

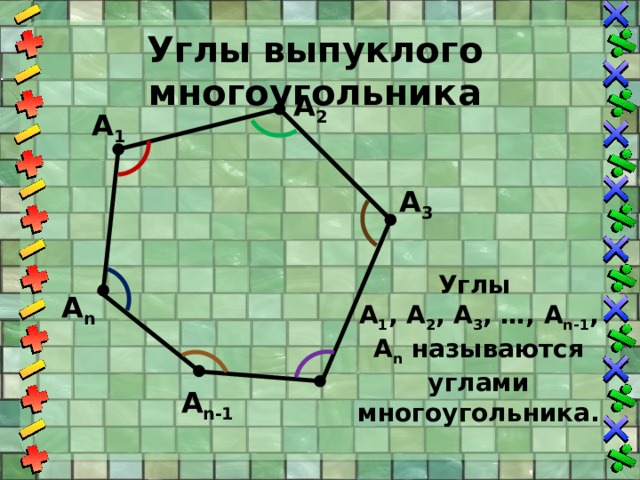
Углы выпуклого многоугольника

А 2

А 1

А 3

Углы

А 1 , А 2 , А 3 , …, A n-1 , A n называются углами многоугольника.

А n

А n-1

А 2

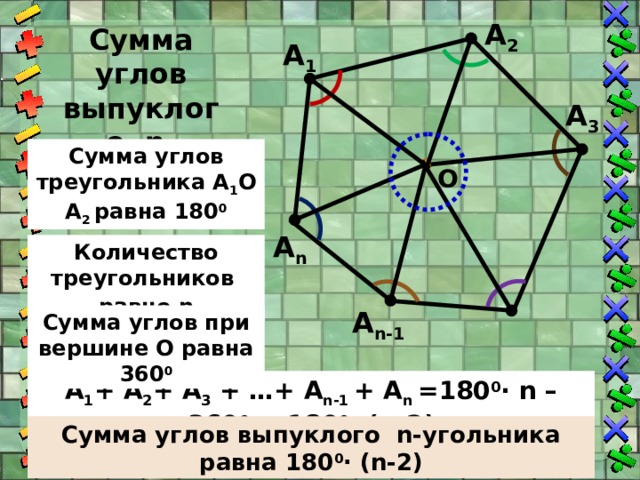
Сумма углов выпуклого n-угольника

А 1

А 3

Сумма углов треугольника А 1 О А 2 равна 180 0

О

А n

Количество треугольников равно n

А n-1

Сумма углов при вершине О равна 360 0

А 1 + А 2 + А 3 + …+ A n-1 + A n =180 0 ∙ n – 360 0 = 180 0 ∙ (n-2)

Сумма углов выпуклого n-угольника равна 180 0 ∙ (n-2)

А 2

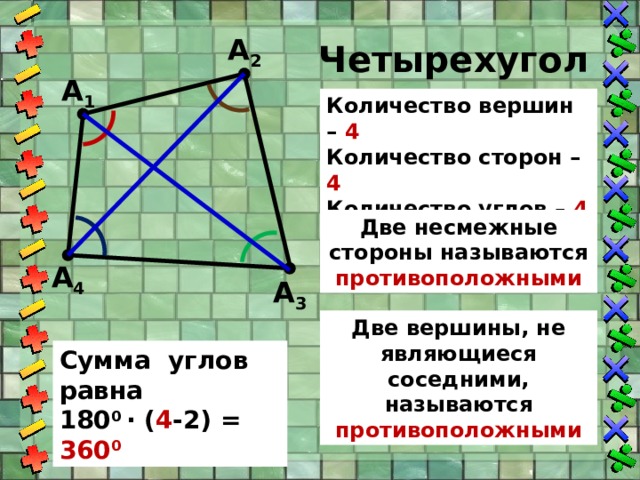
Четырехугольник

А 1

Количество вершин – 4

Количество сторон – 4

Количество углов – 4

Количество диагоналей – 2

Две несмежные стороны называются противоположными

А 4

А 3

Две вершины, не являющиеся соседними, называются противоположными

Сумма углов равна

180 0 ∙ ( 4 -2) = 360 0

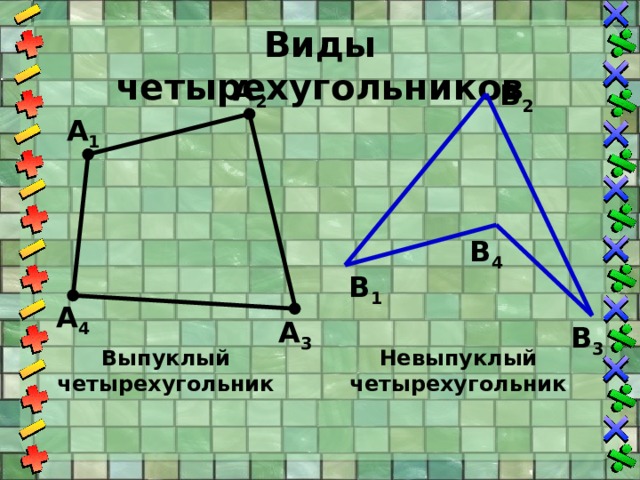
Виды четырехугольников

А 2

В 2

А 1

В 4

В 1

А 4

А 3

В 3

Выпуклый

Невыпуклый

четырехугольник

четырехугольник

ǁ

ǁ

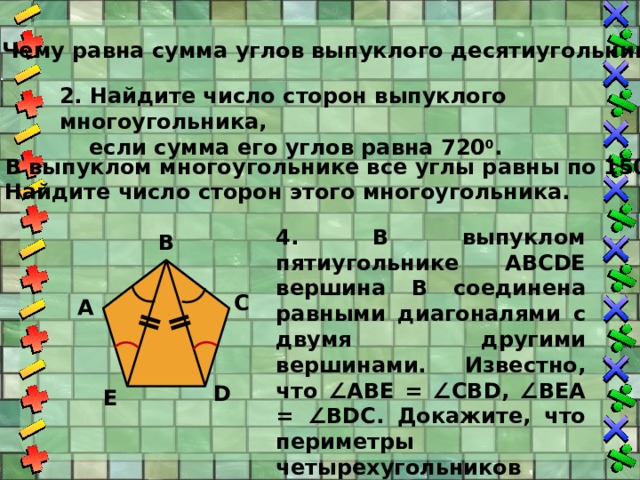
1. Чему равна сумма углов выпуклого десятиугольника?

2. Найдите число сторон выпуклого многоугольника,

если сумма его углов равна 720 0 .

3. В выпуклом многоугольнике все углы равны по 150 0 .

Найдите число сторон этого многоугольника.

4. В выпуклом пятиугольнике АВСDЕ вершина В соединена равными диагоналями с двумя другими вершинами. Известно, что ∠АВЕ = ∠СВD, ∠ВЕА = ∠ВDС. Докажите, что периметры четырехугольников АВDЕ и ВЕDС равны.

В

С

А

D

Е

BC, AB = AD, BC = CD, а прямые, содержащие диагонали четырехугольника пересекаются в точке О. Сравните периметры пятиугольников BCODA и DCOBA. O C A D " width="640"

ǁ

ǁ

∣

ǁ

∣

ǁ

∣

В

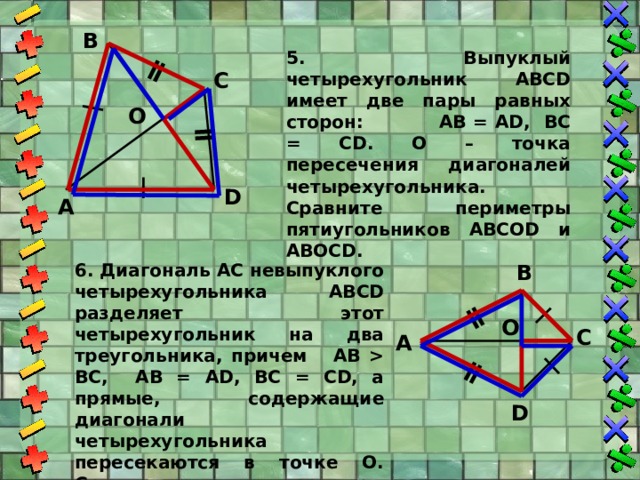
5. Выпуклый четырехугольник АВСD имеет две пары равных сторон: АВ = АD, ВС = СD. О – точка пересечения диагоналей четырехугольника. Сравните периметры пятиугольников АВСОD и АВОСD.

С

О

∣

D

А

B

6. Диагональ АС невыпуклого четырехугольника АВСD разделяет этот четырехугольник на два треугольника, причем АВ BC, AB = AD, BC = CD, а прямые, содержащие диагонали четырехугольника пересекаются в точке О. Сравните периметры пятиугольников BCODA и DCOBA.

O

C

A

D

В

С

D

E

A

F

А

С

D

E

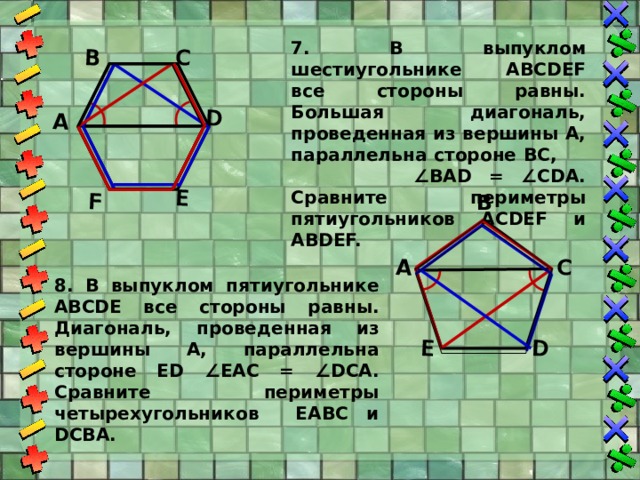
7. В выпуклом шестиугольнике АВСDEF все стороны равны. Большая диагональ, проведенная из вершины А, параллельна стороне ВС, ∠ВАD = ∠СDА. Сравните периметры пятиугольников АСDEF и АВDEF.

B

8. В выпуклом пятиугольнике АВСDE все стороны равны. Диагональ, проведенная из вершины А, параллельна стороне ED ∠EAC = ∠DCА. Сравните периметры четырехугольников EABC и DCBA.