Мультимедийная презентация по математике "Тела вращения"

Математика. Раздел «Геометрия» 1 курс

Тела вращения

Евсюкова Светлана Евгеньевна

преподаватель математики БПОУ ГА «ГАГПК им.М.З.Гнездилова»

Содержание

Шар и сфера

Конус

Тела вращения

Цилиндр

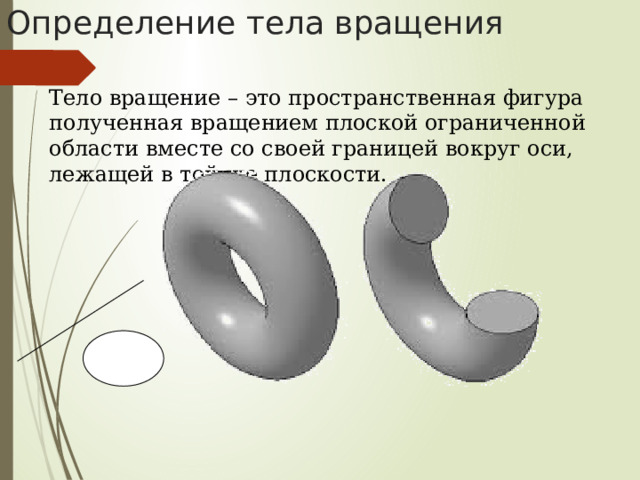
Определение тела вращения

Тело вращение – это пространственная фигура полученная вращением плоской ограниченной области вместе со своей границей вокруг оси, лежащей в той же плоскости.

Задание

1) Приведите примеры из окружающего мира тел, похожих на тело полученное вращением треугольника вокруг оси, содержащей его сторону:

Задание

Из каких геометрических тел состоит тело, полученное вращением трапеции вокруг оси, содержащей большее основание трапеции.

Конусы

Цилиндр

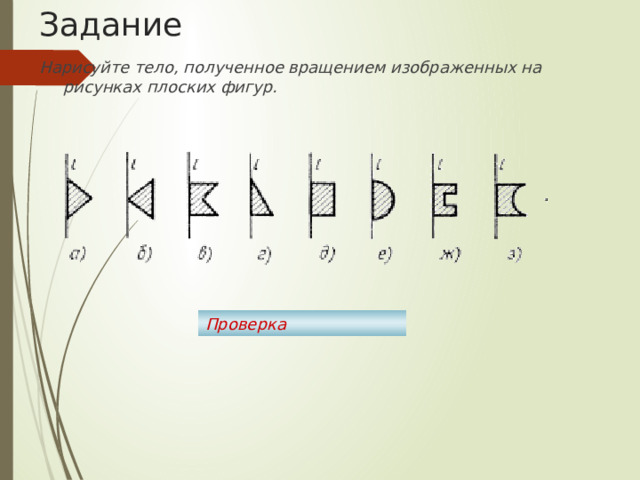
Задание

Нарисуйте тело, полученное вращением изображенных на рисунках плоских фигур.

Проверка

Задание

Нарисуйте тело, полученное вращением изображенных на рисунках плоских фигур.

Задание

Нарисуйте плоскую фигуру, вращая которую можно получить изображенное тело.

В)

А)

Б)

Г)

Д)

Цилиндр

Зададим две параллельные плоскости α и  . В плоскости α расположим окружность некоторого радиуса. Если из каждой точки окружности провести взаимно параллельные прямые пресекающие плоскость  , то в плоскости  получится окружность такого же радиуса. Отрезки прямых, заключенных между параллельными плоскостями образуют в этом случае цилиндрическую поверхность .



Цилиндр – это тело, заключенное между двумя кругами расположенными в параллельных плоскостях и цилиндрической поверхностью.

α

Цилиндр

Цилиндр – это тело, которое описывает прямоугольник при вращении около оси, содержащей его сторону.

Верхний и нижний круги – это основания цилиндра.

Прямая проходящая через центры кругов – это ось цилиндра.

Отрезок параллельный оси цилиндра, концы которого лежат на окружностях основания – это образующая цилиндра.

Радиус основания - это радиус цилиндра.

Высота цилиндра - это перпендикуляр между основаниями цилиндра.

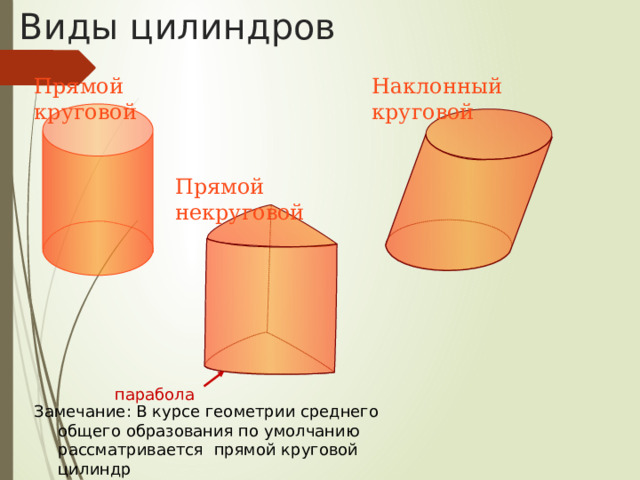
Виды цилиндров

Прямой круговой

Наклонный круговой

Прямой некруговой

парабола

Замечание: В курсе геометрии среднего общего образования по умолчанию рассматривается прямой круговой цилиндр

Сечения цилиндра

Осевое сечение: Плоскость сечения содержит ось цилиндра и перпендикулярна основаниям. В сечении –

прямоугольник.

Сечение плоскостью параллельной оси цилиндра Плоскость сечения параллельна оси цилиндра и перпендикулярна основаниям. В сечении –

прямоугольник.

Сечение плоскостью параллельной основанию цилиндра Плоскость сечения параллельна основаниям цилиндра и перпендикулярна оси. В сечении –

круг.

Замечание: Секущая плоскость может располагаться по-разному, рассмотрим некоторые виды сечений

Площадь поверхности цилиндра

Для вывода формулы площади полной поверхности цилиндра потребуется развертка цилиндра.

Полная поверхность состоит из 2 оснований и боковой поверхности.

Площадь основания находим как площадь круга

S =  R 2

R – радиус основания цилиндра

h

Боковая поверхность цилиндра есть …

2  R

R

прямоугольник.

R

Одна сторона прямоугольника – это высота цилиндра ( h ), другая – длина окружности основания ( 2  R ). Площадь боковой поверхности цилиндра равна произведению сторон прямоугольника.

Получаем, S полн = S бок + 2S осн = 2  Rh + 2  R 2

S полн = 2  R(R + h)

Решение устных задач с цилиндром

1)Во сколько раз увеличится боковая поверхность цилиндра, если его высота увеличится в 5 раз, а радиус основания останется прежним?

R

Ответ: площадь боковой поверхности увеличится в 5 раз.

5h

R

h

Sбок = 2  R5h = 10  Rh

Sбок = 2  Rh

2) Как изменится площадь боковой поверхности цилиндра, если радиус основания увеличится в 2 раза, а высота останется прежней?

R

2R

Ответ: площадь боковой поверхности увеличится в 2 раза.

h

h

Sбок = 2  Rh

Sбок = 2  2Rh = 4  Rh

Решение устных задач с цилиндром

3) Осевые сечения двух цилиндров равны. Равны ли высоты этих цилиндров?

h

2R

2R

Ответ: нет

h

Sсеч = h·2R

Sсеч = 2R·h

4) Стороны прямоугольника равны 4 см и 5 см. Найдите площадь поверхности тела, полученного при вращении этого прямоугольника вокруг меньшей стороны.

5 см

R=5 см, h=4см

4 см

Sполн = 2  R(h + R)= 2  · 5 ·(4 + 5) =90 

Ответ: площадь полной поверхности равна 90  см 2

Решение задач с практическим содержанием

5) Найдите площадь листа жести, если из него изготовлена труба длиной 8 м и диаметром 32 см?

Ответ: 2,56  м 2

Решение

6) Сколько квадратных метров жести израсходовано на изготовление 1 млн. консервных банок диаметром 10 см и высотой 5 см (на швы и отходы добавить 10% материала)?

Решение

Ответ: 11000  м 2

7) Цилиндрический паровой котел имеет диаметр 1 м, длина котла равна 3,8 м, давление пара 10 атм. Найдите силу давления пара на поверхность котла.

Ответ: ≈1,4 · 10 Н

Решение

8) Сколько 2-х килограммовых банок краски нужно купить для окрашивания полуцилиндрического свода подвала длиной 6 м и высотой 2,9 м. Расход краски 100 г на 1 м 2.

Ответ: 3 банки

Решение

Решение задачи 5

5) Найдите площадь листа жести, если из него изготовлена труба длиной 8 м и диаметром 32 см?

Дано: цилиндр, h = 8 м, d = 32 см.

Найти: S бок

8 м

S - ?

32 см

d = 32 cм = 0,32 м; d = 2R

S бок =  dh;

S бок =  ·0,32·8 = 2,56 

Ответ: 2,56  м 2

Решение задачи 6

6) Сколько квадратных метров жести израсходовано на изготовление 1 млн. консервных банок диаметром 10 см и высотой 5 см (на швы и отходы добавить 10% материала)?

Дано: цилиндр, h = 5 см, d = 10 см, n = 1 млн. штук

Найти: S материала

S, м 2 - ?

5см

10 см

S материала = n· S банки 1) Найдем количество материала на изготовление 1 банки:

d = 2R, R = 0,5d= 5см, S полн = 2  R(R+h); S полн =  ·2·5 ·(5 + 5) = 100  (см 2 )

10% = 0,1; S банки = 100  + 0,1·100  = 110  (см 2 ) 2) S материала = 1000000 ·110  = 11 ·10 7  (см 2 ),

1м 2 = 10000 см 2 ; S материала = 11000  (см 2 ).

Ответ: 11000  м 2 ≈ 34540 м 2

Решение задачи 8

8) Сколько 2-х килограммовых банок краски нужно купить для окрашивания полуцилиндрического свода подвала длиной 6 м и высотой 2,9 м. Расход краски 100 г на 1 м 2.

Дано: h = 6 м, R = 2,9 м, m банки = 2 кг, 100 г на 1 м 2

Найти: n – количество банок

6 м

2,9 м

1) Вычислим площадь поверхности, которую нужно покрасить:

S свода = 0,5S бок =0,5 ·2·2,9 ·6  = 17,4  ≈17,4 ·3,14 = 54,636(м 2 )

2) На 1 м 2 расходуется 100 г = 0,1 кг краски, значит на окраску свода потребуется 54,636 · 0,1 = 5,4636 (кг) краски,

т. к. банки по 2 кг, то 5,4636 : 2 ≈ 3 банки краски

Ответ: 3 банки краски

Конус

Зададим плоскость α и точку С вне этой плоскости. В плоскости α расположим окружность некоторого радиуса. Проведем прямые проходящие через точку С и все точки окружности. Поверхность, образованная отрезками с концами на окружности и в точке С образуют коническую поверхность .

С

Конус – это тело, ограниченное конической поверхностью и кругом, включая окружность.

α

Конус

Конус – это тело, которое описывает прямоугольный треугольник при вращении вокруг оси, содержащей его катет.

• Круг – это основание конуса.

• Точка вне круга с которой соединяются все точки окружности – это вершина конуса.

• Прямая проходящая через центр круга и вершину конуса – есть ось конуса.

• Отрезок соединяющий вершину с любой точкой окружности основания – это образующая конуса.

• Радиус основания - это радиус конуса.

• Высота конуса - это перпендикуляр, опущенный из вершины конуса к основанию.

Замечание: так как ось перпендикулярна основанию и проходит через вершину, то высота конуса лежит на его оси.

Конические сечения

1) Если плоскость пересекает все образующие конической поверхности, то в сечении получается эллипс .

2) Если плоскость сечения параллельна одной из образующих, то в сечении получается парабола .

3) Если плоскость сечения пересекает обе полости конической поверхности, то в сечении получается гипербола .

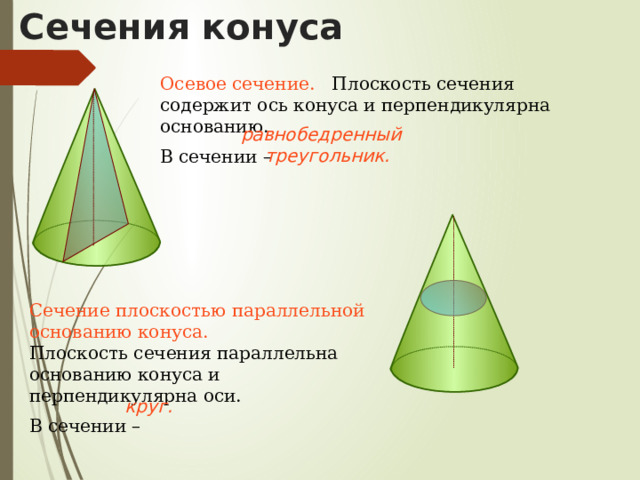
Сечения конуса

Осевое сечение. Плоскость сечения содержит ось конуса и перпендикулярна основанию.

В сечении –

равнобедренный треугольник.

Сечение плоскостью параллельной основанию конуса. Плоскость сечения параллельна основанию конуса и перпендикулярна оси.

В сечении –

круг.

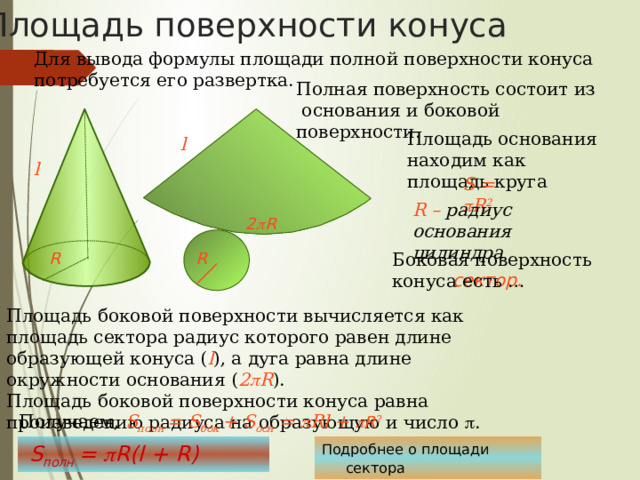
Площадь поверхности конуса

Для вывода формулы площади полной поверхности конуса потребуется его развертка.

Полная поверхность состоит из основания и боковой поверхности.

Площадь основания находим как площадь круга

l

l

S =  R 2

R – радиус основания цилиндра

2  R

Боковая поверхность конуса есть …

R

R

сектор.

Площадь боковой поверхности вычисляется как площадь сектора радиус которого равен длине образующей конуса ( l ), а дуга равна длине окружности основания ( 2  R ). Площадь боковой поверхности конуса равна произведению радиуса на образующую и число  .

Получаем, S полн = S бок + S осн =  Rl +  R 2

S полн =  R(l + R)

Подробнее о площади сектора

Площадь сектора

r – радиус круга, α – величина дуги в градусах, R – радиус основания конуса, l – длина образующей конуса

r = l

α

Вычисляя боковую поверхность конуса вписываем в данную формулу новые обозначения и выражаем α через радиус ( R ) и образующую ( l ) . Длина дуги сектора равна длине окружности основания конуса 2  R , с другой стороны ее можно вычислить по формуле для длины дуги. Получаем равенство:

Выразим α и подставим в формулу площади сектора круга.

Содержание

Решение устных задач с конусом

1)Во сколько раз увеличится боковая поверхность конуса, если его образующая увеличится вдвое, а радиус основания одновременно увеличится в 3 раза?

2l

l

Ответ: площадь боковой поверхности увеличится в 6 раз.

3R

R

Sбок =  3R2l = 6  Rl

Sбок =  Rl

2) Вычислите площадь боковой и полной поверхностей конуса, длина образующей которого равна 10 см, а радиус основания 3 см.

Sосн =  R 2 =  · 3 2 = 9  (см 2 )

Sбок =  3·10 = 30  (см 2 )

10

Sполн = 39  (см 2 )

Ответ: 30  см 2 , 39  см 2

3

Решение задач

3) Коническая крыша башни имеет диаметр 6 м и высоту 2 м. сколько листов кровельного железа потребуется для этой крыши, если размер листа 0,7 м x 1,4 м, а на швы и обрезки тратится 10% от площади крыши.

1,4 м

0,7 м

2 м

1) Вычислим площадь листа кровельного железа 0,7 · 1,4 = 0,98 м 2

2) вычислим радиус, конуса R = 0,5 d= 0,5 · 6 = 3 (м), h– высота конуса, h = 2 м. 3) Образующую конуса найдем по теореме Пифагора

2

l

4) Sбок =  Rl =  ·3 · √13 = 3√13  (м 2 )

3

S материала = 3√13  + 0,1 · 3√13  = 3,3√13  (м 2 )

S материала ≈ 37,36 м 2

5) Вычислим количество листов кровельного железа 37, 36 : 0,98 = 38,12 ≈ 39

Ответ: количество листов равно 39 штук.

Определение шара

Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного, от заданной точки точки.

Эта точка называется центром шара.

Расстояние от центра шара до любой точки поверхности называется – радиусом шара

Шар можно получить вращением полукруга вокруг оси, содержащей его диаметр.

Сфера – это поверхность все точки которой равноудалены от заданной точки.

Сечения шара

Сечение шара, проходящее через его центр.

В сечении –

круг.

В этом случае в сечении получается круг наибольшего радиуса, его называют большой круг шара .

Сечение плоскостью, не проходящей через центр.

В сечении –

круг.

Теорема: Площадь поверхности шара равна четыре площади большого круга шара.

S = 4  R 2

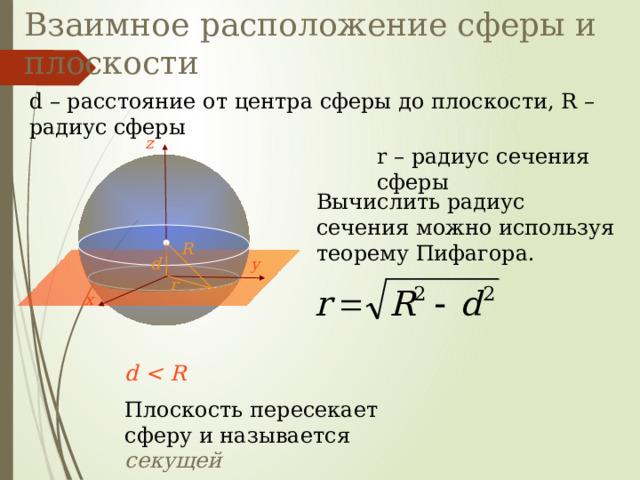
Взаимное расположение сферы и плоскости

d – расстояние от центра сферы до плоскости, R – радиус сферы

z

r – радиус сечения сферы

Вычислить радиус сечения можно используя теорему Пифагора.

R

y

d

r

x

d

Плоскость пересекает сферу и называется секущей

Взаимное расположение сферы и плоскости

d – расстояние от центра сферы до плоскости, R – радиус сферы

z

Теорема: Радиус сферы проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.

R

y

x

d = R

Плоскость имеет одну общую точку со сферой и называется касательной

R Плоскость не имеет общих точек со сферой. y x " width="640"

Взаимное расположение сферы и плоскости

d – расстояние от центра сферы до плоскости, R – радиус сферы

z

d R

Плоскость не имеет общих точек со сферой.

y

x

Решение задач

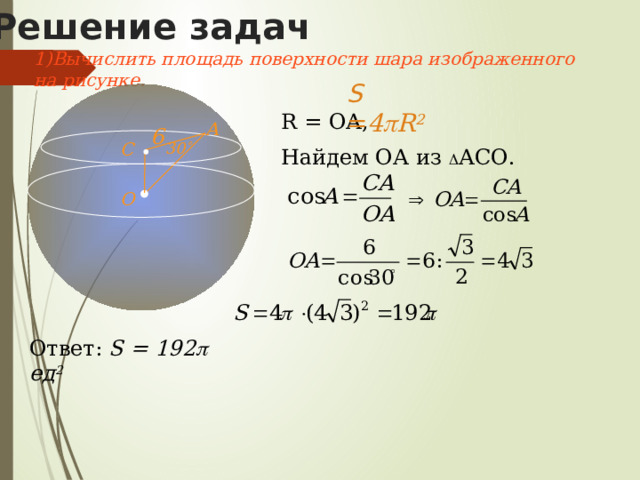
1)Вычислить площадь поверхности шара изображенного на рисунке.

S = 4  R 2

R = ОА,

Найдем ОА из  АСО.

А

6

С

30 

О

Ответ: S = 192  ед 2

Решение задач

2) Наибольшая высота орбиты корабля «Восток-2», на котором летал космонавт Г.С. Титов, равна 244 км. Найдите угол, под которым космонавт видел Землю в момент наибольшего удаления от нее (радиус Земли примерно равен 6371 км).

О - центр Земли, А – точка орбиты в которой находится корабль, В и С – точки касания.

 ВАС - искомый угол.

Углы В и С прямые, теорема о радиусе проведенном в точку касания.  АВО =  АСО, т.к. АО общая, АВ= АС как отрезки касательных   ВАО =  САО.

ОА = 6371 + 244 = 6615 км, ОВ = 6371 км

В

А

  ВАО = 74  23`,

значит  ВАС = 148  46`≈149  .

О

С

R з

Ответ: Космонавт видит Землю под углом ≈149 

Литература

• Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия, 10-11: Учеб. для общеобразоват. учреждений. – М.: Просвещение, 2019.
• Бевз Г.П. и др. Геометрия: Учеб. для 7-11 кл. общеобразоват. учреждений. – М.: Просвещение, 1994.
• Глейзер Г.Д. Геометрия: Учеб. пособие для 10-12 кл.веч. (смен.) шк. и самообразования. – М.: Просвещение, 1989.
• Клопский В.М., Скопец З.А., Ягодовский М.И. Геометрия: Учеб. пособие для 9 и 10 классов. – М.: Просвещение, 1980.