Начальные сведения из теории вероятностей

Начальные сведения из теории вероятностей

Автор: Софронова Наталия Андревна,

учитель математики МОУ «Упшинская ООШ»

Оршанского района Республики Марий Эл

(К учебнику Ю.Н.Макарычева и др.«Алгебра, 9 класс», 2008 г.)

Случайные события

Случайное событие - это событие,

которое может произойти или не произойти

Примеры:

Выпадение орла или решки при подбрасывании монеты.

Поражение мишени или промах при выстреле.

Выигрыш, проигрыш или ничейный результат спортивной команды при встрече с соперником.

Теория вероятностей

• Закономерности случайных событий изучает специальный раздел математики, который называется теорией вероятностей.

• Методы теории вероятностей применяются в

• информатике,
• физике,
• астрономии,
• биологии,
• медицине

Зарождение теории вероятностей

Поиск ответа на вопрос

• Как часто наступает то или иное событие в большой серии происходящих в одинаковых условиях испытаний со случайными исходами ?

Пример

• Бросали 100 раз игральный кубик и наблюдали, сколько раз на верхней грани кубика выпадет шесть очков.
• При бросании игрального кубика на его верхней грани может выпасть одно, два, три, четыре, пять, шесть очков. Каждое из этих шести событий ( шести исходов испытания ) является случайным.
• Допустим, что в данной серии экспериментов «шестерка» выпала 17 раз.
• Число 17 называют частотой события
• Отношение частоты к общему числу испытаний равное 17 / 100 называют относительной частотой этого события .

• Относительной частотой случайного события в серии испытаний называется отношение числа испытаний, в которых это событие наступило, к числу всех испытаний

Орел или решка ?

• Пример.

• Подбрасывают монету и отмечают, упадет она кверху орлом или решкой.
• Если монета однородна и имеет правильную геометрическую форму, то шансы выпадения орла или решки одинаковы.
• При небольшом числе испытаний выпадение, например, орла может произойти чаще, чем выпадение решки. Однако, если эти испытания производятся большое число раз, то относительная частота выпадения орла близка к относительной частоте выпадения решки.

Вероятность события

• К.Пирсон, английский ученый (1857-1936) бросал монету 24000 раз. В этом испытании монета упала кверху орлом 12012 раз, значит относительная частота выпадения орла равна

12012 : 24000 = 0,5005

• В.И.Романовский, российский ученый (1879-1954) подбрасывал монету 80640 раз. В этом испытании монета упала кверху орлом 39699 раз, значит относительная частота выпадения орла равна

39699 : 80640 = 0,4923

• Аналогичные опыты проделывали и другие ученые. Оказалось, что каждый раз относительная частота выпадения орла незначительно отличалась от ½.

• Говорят, что вероятность события « выпал орел при подбрасывании однородной монеты, имеющей правильную геометрическую форму», равна ½

Статистический подход

Если в длинной серии одинаковых экспериментов со случайными исходами значения относительных частот появления одного и того же события близки к некоторому определенному числу , то это число принимают за вероятность данного случайного события.

Такой подход к вычислению вероятностей называют статистическим

Вероятность случайного события оценивают, когда в ходе исследования анализируют относительную частоту наступления этого события при многократном повторении в одних и тех же условиях эксперимента или наблюдения.

Примеры:

• Определение всхожести семян некоторого растения.
• Предсказание результатов выступления спортсмена в соревнованиях по стрельбе

Вероятность равновозможных событий

• Для того, чтобы оценить вероятность интересующего нас события путем статистического исследования, необходимо провести большое число опытов или наблюдений , и только после этого определить приближенно вероятность этого события. В то же время в ряде случаев вероятность события можно оценить исходя из условий самого опыта или наблюдения путем рассуждений, не прибегая к испытаниям
• Если кубик имеет правильную форму и сделан из однородного материала, то при его бросании шансы выпадения на его верхней грани каждого числа очков от 1 до 6 одинаковы, то есть нет никаких оснований считать, что какой-нибудь из исходов более возможен, чем остальные.
• Говорят, что существует 6 равновозможных исходов опыта с бросанием кубика: выпадение 1 очка, выпадение 2 очков, выпадение 3 очков, выпадение 4 очков, выпадение 5 очков, выпадение 6 очков.

• Вообще исходы в определенном опыте или наблюдении считают равновозможными, если шансы этих исходов одинаковы.

Благоприятные исходы

• Исходы, при которых происходит некоторое событие, называются благоприятными для этого события.

• Событие В: выпадение на кубике числа очков, кратного 3.

Это событие происходит лишь при двух исходах испытания: когда выпало 3 очка и когда выпало 6 очков, то есть для события В благоприятными являются два исхода из шести равновозможных исходов.

• Отношение числа благоприятных исходов к числу всех равновозможных исходов равно 2 / 6 .
• Это отношение считают вероятностью события В и пишут: Р(В) = 2 / 6
• Р – первая буква французского слова probabilite ( вероятность )

Классический подход

Задача 1. Найдем вероятность того, что при подбрасывании двух монет на обеих монетах выпадет решка.

• При одновременном бросании двух монет равновоможными являются следующие исходы:

1 монета – орел, 2 монета – орел

1 монета – орел, 2 монета - решка

1монета – решка, 2 монета - орел

1 монета – решка, 2 монета – решка

• Событие А: на обеих монетах выпадет решка

• Благоприятный исход – 1
• Количество равновозможных исходов – 4
• Р(А) = 1 / 4

Задача 2. Из 25 экзаменационных билетов по геометрии ученик выучил 11 первых и 8 последних билетов. Какова вероятность того, что на экзамене ему достанется билет, который он не подготовил?

• Событие М: ученику достанется билет, который он не выучил
• Общее число равновозможных исходов при выборе билетов – 25.

• Число благоприятных для события М исходов равно 25 – (11+8) = 6

• Р(М) = 6 / 25

Задача 3. Антон и Игорь бросают белый и черный игральные кубики и подсчитывают сумму выпавших очков. Они договорились, что если при очередном бросании в сумме выпадет 8 очков, то выигрывает Антон. Если в сумме выпадет 7 очков, то выигрывает Игорь. Можно ли считать, что шансы выиграть в этой игре у мальчиков одинаковые?

• Событие А: в сумме выпадет 8 очков
• Событие В: в сумме выпадет 7 очков
• При бросании кубиков на белом кубике может выпасть 1, 2, 3, 4, 5 или 6 очков. Каждому числу очков, выпавших на белом кубике, соответствует шесть вариантов очков, выпавших на черном кубике.

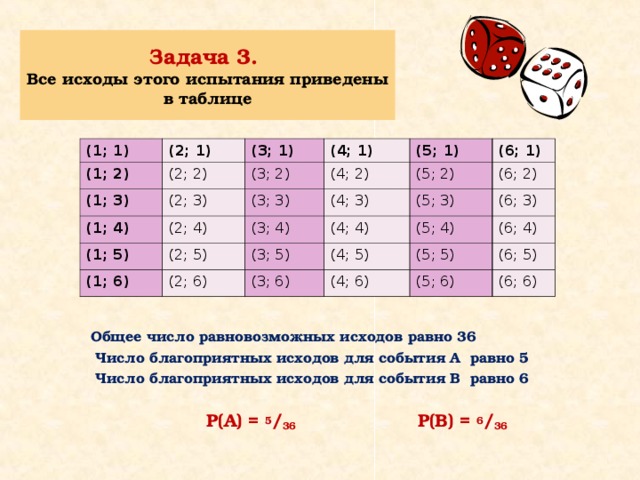
Задача 3. Все исходы этого испытания приведены в таблице

(1; 1)

(1; 2)

(2; 1)

(2; 2)

(1; 3)

(3; 1)

(4; 1)

(1; 4)

(3; 2)

(2; 3)

(4; 2)

(2; 4)

(5; 1)

(1; 5)

(3; 3)

(1; 6)

(3; 4)

(2; 5)

(5; 2)

(4; 3)

(6; 1)

(2; 6)

(6; 2)

(4; 4)

(3; 5)

(5; 3)

(3; 6)

(4; 5)

(6; 3)

(5; 4)

(6; 4)

(4; 6)

(5; 5)

(6; 5)

(5; 6)

(6; 6)

Общее число равновозможных исходов равно 36

Число благоприятных исходов для события А равно 5

Число благоприятных исходов для события В равно 6

Р(А) = 5 / 36 Р(В) = 6 / 36

Задача 4. Из 16 собранных велосипедов 4 оказались с дефектами. Какова вероятность того, что 2 выбранных наугад велосипеда будут без дефектов?

• Событие А: 2 выбранных велосипеда будут без дефектов.
• Общее число равновозможных исходов при выборе двух велосипедов из 16 равно числу сочетаний из 16 по 2 .

• Число благоприятных для события А исходов при выборе двух велосипедов из 12 исправных равно числу сочетаний из 12 по 2

• Р(А) = 66 / 120 = 0,55

Задача 5 Группа туристов, в которой 7 юношей и 4 девушки выбирает по жребию четырех дежурных. Какова вероятность того, что будут выбраны 2 юноши и 2 девушки?.

• Событие А: будут выбраны 2 юноши и 2 девушки
• Общее число равновозможных исходов при выборе четырех дежурных из 11 человек равно

• Число благоприятных для события А исходов равно

• Р (А) = 126 /330

Достоверное событие

Событие, которое при проведении некоторого опыта или наблюдения происходит всегда, называют достоверным событием.

• Вероятность достоверного события равна 1.

Пример достоверного события

Событие С: при бросании игрального кубика выпадет менее 7 очков

Общее число равновозможных исходов - 6

Число благоприятных для события С исходов - 6

• Р (С) = 6 / 6 =1

Невозможное событие

Событие, которое не может произойти ни при каком исходе опыта или наблюдения, называют невозможным событием.

• Вероятность невозможного события равна 0.

Пример невозможного события

Событие М: при бросании игрального кубика выпадет 7 очков.

Общее число равновозможных исходов - 6

Число благоприятных для события С исходов - 0

• Р (С) = 0 / 6 =0

С - некоторое событие Р(С) – вероятность наступления этого события

Задача 6 . Участники игры поочередно бросают в мишень дротики. Мишень представляет собой круг, в котором выделены малый круг и кольцевая зона, причем радиус малого круга в 2 раза меньше радиуса большого круга. Найти вероятность того, что при попадании дротика в мишень точка попадания окажется в кольцевой зоне.

Событие А: точка попадания дротика окажется в кольцевой зоне .

• Пусть радиус малого круга равен R ,
• тогда радиус большого круга равен 2R .
• Площадь малого круга равна …
• Площадь большого круга равна …
• Площадь кольца равна ...
• Р(А) равна отношению площади кольца к площади большого круга, то есть …

Несовместные события

Два события называются несовместными , если в одном и том же испытании они не могут произойти одновременно, то есть наступление одного из них исключает наступление другого.

Пример несовместных событий

Пусть в коробке находится 19 шаров: 10 белых, 4 красных и 5 зеленых. Из коробки наугад вынимают один шар. Рассмотрим такие события:

событие А – шар оказался красным ;

событие В – шар оказался зеленым .

События А и В не могут произойти одновременно. Они являются несовместными.

Сложение вероятностей

Событие А – шар оказался красным .

Событие В – шар оказался зеленым .

Событие С - шар оказался не белым

(красным или зеленым).

Не белых шаров – 9 (4 красных и 5 зеленых)

Р(А) = 4 / 19

Р(В) = 5 / 19

Р(С) = 9 / 19

Вывод:

Р(С) = Р(А) + Р(В)

Если событие С означает, что наступает одно из двух несовместных событий А или В, то вероятность события С равна сумме вероятностей событий А и В.

Сложение вероятностей

Задача 7.

На карточках написали натуральные числа от 1 до 10 включительно, после чего карточки перевернули и перемешали. Затем наугад открыли одну карточку. Какова вероятность того, что на ней написано простое число или число , большее 7?

• Событие А: на карточке простое число .
• Событие В: на карточке число, большее 7 .
• Событие С : на карточке простое число или число , большее 7.

• Найдем Р(С).

Сложение вероятностей

Решение.

Всего исходов - 10

• Исходы, благоприятные для события А ( на карточке простое число) – 2,3,5,7.
• Р(А) = 4 / 10 = 0, 4.
• Исходы, благоприятные для события В ( на карточке число, большее 7) – 8, 9,10.
• Р(В) = 3 / 10 = 0,3.
• А и В – несовместны.
• Событие С означает, что наступает одно из двух несовместных событий А или В, поэтому:
• Р(С) = Р(А) + Р(В) = 0,4 + 0,3 = 0,7

Противоположные события

Бросают игральный кубик.

Событие А: выпало 6 очков.

Событие В: выпало менее 6 очков.

А и В – противоположные события (если наступит событие А, то событие В не наступит, и наоборот).

Р(А) = 1/6, Р(В) = 5/6, Р(А) + Р(В) = 1

Сумма вероятностей противоположных событий равна 1.

Противоположные события

При решении некоторых задач бывает удобно воспользоваться свойством вероятностей противоположных событий

Противоположные события

Задача 8.

Бросают два игральных кубика. Какова вероятность того, что сумма очков, выпавших на двух кубиках, меньше 11?

Независимые события

Пусть в одном из двух ящиков находится 15 деталей, из которых 2 нестандартные, а в другом – 20 деталей, из которых 3 нестандартные. Из каждого ящика вынимают по одной детали. Какова вероятность того, что обе детали окажутся нестандартными?

Событие А: из первого ящика вынимают нестандартную деталь.

Событие В: из второго ящика вынимают нестандартную деталь.

А и В – независимые события (вероятность наступление одного из них не влияет на вероятность наступления другого события).

Независимые события

Задача 9.

Пусть в одном из двух ящиков находится 15 деталей, из которых 2 нестандартные, а в другом – 20 деталей, из которых 3 нестандартные. Из каждого ящика вынимают по одной детали. Какова вероятность того, что обе детали окажутся нестандартными?

Решение.

Событие А: из первого ящика вынимают нестандартную деталь.

Р(А) = 2 / 15 .

Событие В: из второго ящика вынимают нестандартную деталь.

Р(В) = 3 / 20

А и В – независимые события.

Независимые события

Независимые события

Если событие С означает совместное наступление двух независимых событий А и В, то вероятность события С равна произведению вероятностей событий А и В.

Р(С) = Р(А) ∙ Р(В)

Независимые события

Задача 10.

В непрозрачном пакете лежат 9 жетонов с номерами 1, 2, …, 9. Из пакета наугад вынимают жетон, записывают его номер и возвращают в пакет. Затем опять вынимают жетон и записывают его номер. Какова вероятность того, что оба раза будут вынуты жетоны, номера которых являются простыми числами?

Независимые события

Независимые события

Задача 11.

В результате многократных наблюдений установили, что вероятность попадания в мишень одного стрелка равна 0,9, а другого – 0,8. Каждый из стрелков сделал по одному выстрелу из мишени. Какова вероятность того, что мишень будет пораженной?

Решение.

Событие А – первый стрелок попал в мишень.

Событие В - второй стрелок попал в мишень.

Событие С – мишень поражена.

События А и В – независимы.

Событие С не означает их совместного наступления.