Некоторые свойства окружности. Касательная

Некоторые свойства окружности. Касательная к окружности

7 класс

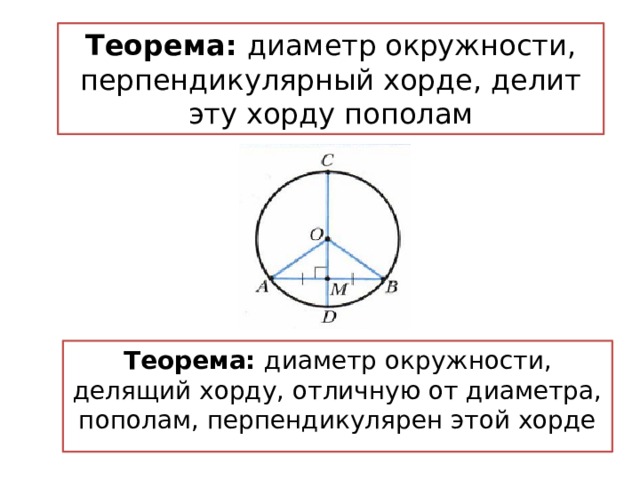
Теорема: диаметр окружности, перпендикулярный хорде, делит эту хорду пополам

Теорема: диаметр окружности, делящий хорду, отличную от диаметра, пополам, перпендикулярен этой хорде

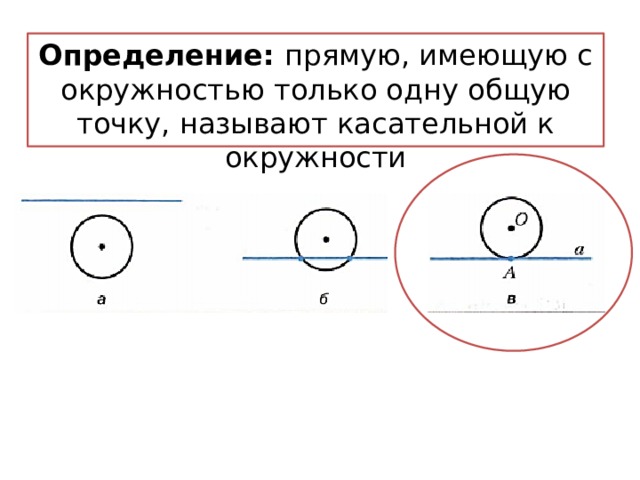
Определение: прямую, имеющую с окружностью только одну общую точку, называют касательной к окружности

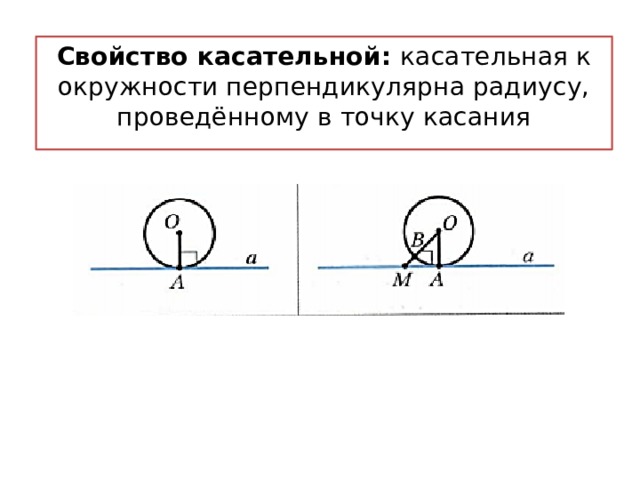
Свойство касательной: касательная к окружности перпендикулярна радиусу, проведённому в точку касания

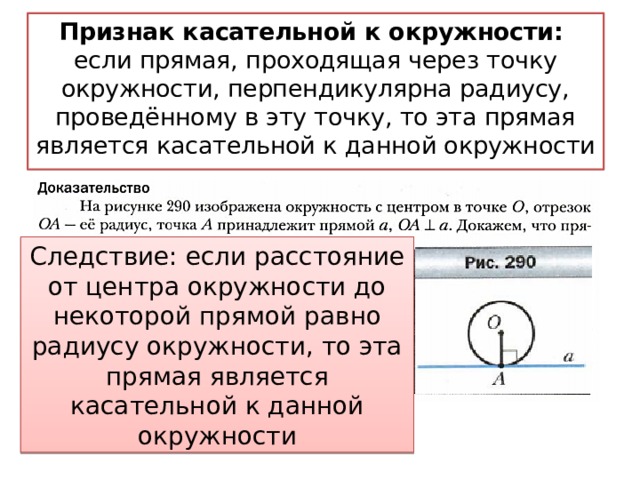
Признак касательной к окружности:

если прямая, проходящая через точку окружности, перпендикулярна радиусу, проведённому в эту точку, то эта прямая является касательной к данной окружности

Следствие: если расстояние от центра окружности до некоторой прямой равно радиусу окружности, то эта прямая является касательной к данной окружности

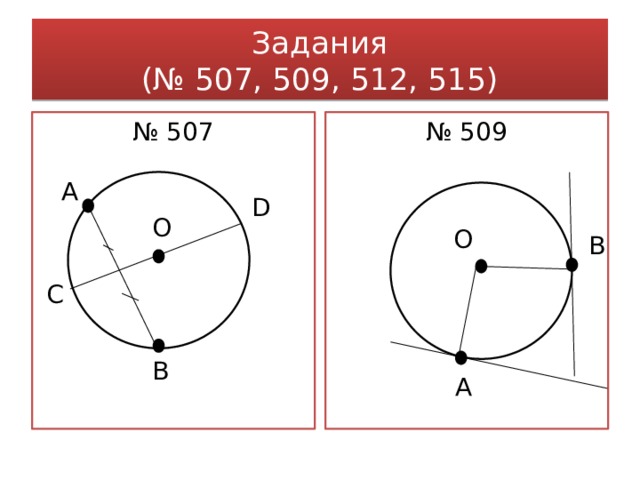
Задания (№ 507, 509, 512, 515)

№ 509

№ 507

А

D

О

О

B

С

В

А

Задания (№ 507, 509, 512, 515)

А

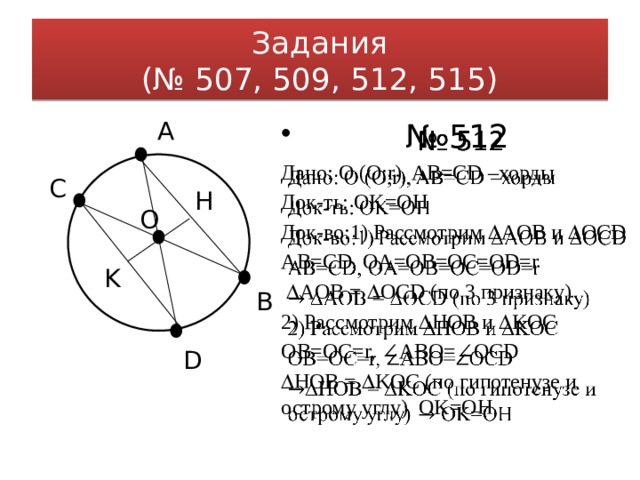
№ 512

Дано: O (O;r), AB=CD –хорды

Док-ть: OK=OH

Док-во:1) Рассмотрим  AOB и  OCD

AB=CD, OA=OB=OC=OD=r

 AOB =  OCD (по 3 признаку)

2) Рассмотрим  HOB и  KOC

OB=OC=r, ∠ABO=∠OCD

 HOB =  KOC (по гипотенузе и острому углу) OK=OH

C

H

О

K

B

D

Задания (№ 507, 509, 512, 515)

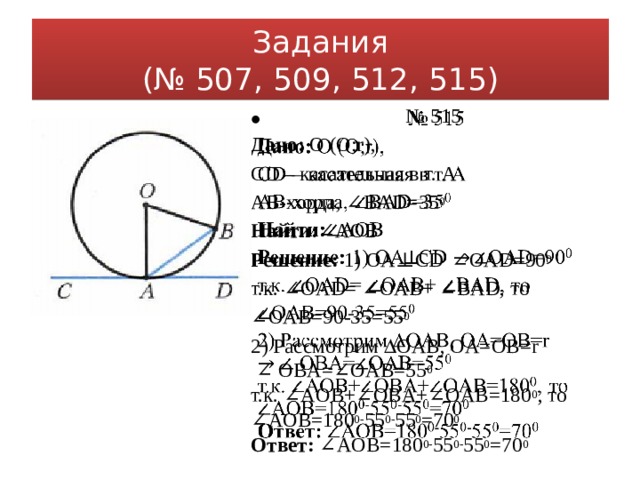
№ 515

Дано: O (O;r),

CD – касательная в т. A

AB-хорда, ∠BAD=35 0

Найти: ∠AOB

Решение: 1) OA⊥CD ∠OAD=90 0

т.к. ∠OAD= ∠OAB+ ∠BAD, то

∠ OAB=90-35=55 0

2) Рассмотрим  OAB, OA=OB=r

∠ OBA=∠OAB=55 0

т.к. ∠AOB+∠OBA+∠OAB=180 0 , то

∠ AOB=180 0- 55 0- 55 0 =70 0

Ответ: ∠AOB=180 0- 55 0- 55 0 =70 0

Домашняя работа

П. 20, вопросы разобрать

№ 511, 516

Спасибо за внимание!