МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«Национальный исследовательский ядерный университет «МИФИ»
Московский областной политехнический колледж –
филиал федеральное государственное автономное образовательное
учреждение высшего профессионального образования «Национальный
исследовательский ядерный университет «МИФИ»
(МОПК НИЯУ МИФИ)
Методическое пособие для студентов
Краткий курс лекций по теме
Неопределенный интеграл и его приложение
(название)
Рассмотрено на заседании ПЦК
физико-математических дисциплин
Протокол № ____ от «____» ___________ 2016 г.
Председатель ПЦК Л.А. Кувшинова___________
Разработал преподаватель математики
Е.Н. Лебедева _____________________________
г. Электросталь 2020 г.
СОДЕРЖАНИЕ
| Пояснительная записка…………………………………….………………... | 3 |
| 1. | Теоретическая часть……………………………………………………... | 6 |
|
| 1.1. | Неопределенный интеграл и его свойства……………………...... | 6 |
|
|
| 1.1.1. Первообразная функции……………………………………. | 6 |
|
|
| 1.1.2. Неопределенный интеграл и его простейшие свойства...... | 7 |
|
|
| 1.1.3. Основные формулы интегрирования……………………… | 9 |
|
| 1.2. | Методы интегрирования………………………………………….. | 10 |
|
|
| 1.2.1. Метод непосредственного интегрирования……………...... | 10 |
|
|
| 1.2.2. Интегрирование методом замены переменной (способ подстановки)……………………………………………………….. |
11 |
|
|
| 1.2.3. Интегрирование по частям…………………………………. | 12 |
|
|
| 1.2.4. Интегрирование рациональных дробей…………………… | 14 |
|
|
| 1.2.5. Интегрирование некоторых тригонометрических функций………………………………………………………….… |
14 |
|
| 1.3. | Приложения неопределенного интеграла………………………... | 15 |
|
|
| 1.3.1. Нахождение первообразной по начальным условиям…..... | 15 |
|
|
| 1.3.2. Выделение из семейства кривых с одинаковым наклоном линии, проходящей через конкретную точку…………………… |
16 |
|
|
| 1.3.3. Составление уравнения движения тела по заданному уравнению скорости или ускорения……………………………... |
17 |
| 2. | Практическая часть…………………………………………………….... | 18 |
|
| 2.1. | Примеры решения задач………………………………………..…. | 18 |
|
| 2.2 | Задачи для самостоятельного решения………………………..…. | 27 |
| Ответы………………………………………………………………………… | 29 |
| Список литературы…………………………………………………………... | 30 |
Пояснительная записка
Настоящее пособие предназначено для студентов как дневных, так и заочных отделений колледжа, а также может быть использовано для самостоятельного изучения темы, закрепления пройденного материала, овладения способами и методами решения задач в объеме действующей программы по математике для средних профессиональных учебных заведений.
Целью и основными задачами данной разработки являются пополнение знаний студентов основами математических знаний, умений и навыков в объеме, необходимом для их повседневной практической деятельности, для дальнейшей учебы и работы по специальности, для усвоения общетехнических и специальных предметов, а также для дальнейшего повышения квалификации путем самообразования, обеспечение выпускнику конкурентоспособности на рынке труда.
Изучение темы «Неопределенный интеграл и его приложение» направлено на развитие гибкости мышления студентов, на привитие алгоритмической культуры. Именно поэтому изучение основных формул интегрирования и умение их использовать в процессе решения упражнений имеют большое практическое и воспитательное значение. Понятие интеграла является фундаментальным понятием математического анализа, находящим обширные приложения в различных областях науки и техники. Именно поэтому необходимо глубокое и осознанное изучение этого понятия.
Решение задач по математике у студентов колледжей часто сопряжено со многими трудностями. Помочь студентам преодолевать эти трудности, научить применять теоретические знания к решению задач – основное назначение настоящего пособия.
Методика изложения материала в пособии определяется, прежде всего, тем, что это пособие предназначено для студентов, не имеющих пока среднего образования, а потому не готовых к полноценному усвоению математического анализа в традиционном изложении. Поэтому в пособии введение определений и доказательство теорем сопровождаются достаточным количеством геометрических иллюстраций.
Пособие содержит программный материал. В данном пособии весь теоретический материал изложен доступно для большинства учащихся. Это способствует решению важной педагогической задачи – научить работать с источником.
В работе представлены теоретические сведения, необходимые для усвоения материала и решения задач.
В пособии даны алгоритмы решений типовых задач. Алгоритм – это совокупность четко определенных правил решения задач за конечное число шагов или последовательность выполняемых действий. Алгоритмы развивают логику, являются основой составления программ в работе с компьютером; алгоритмы используются в любой сфере деятельности человека.
Пособие состоит из двух частей.
В первой части рассматривается основные понятие, связанные с неопределенным интегралом: первообразная функции, простейшие свойства неопределенного интеграла, основные формулы интегрирования, методы интегрирования (метод непосредственного интегрирования, интегрирование методом замены переменной (способ подстановки), интегрирование по частям, интегрирование рациональных дробей, интегрирование некоторых тригонометрических функций), приложения неопределенного интеграла (нахождение первообразной по начальным условиям, выделение из семейства кривых с одинаковым наклоном линии, проходящей через конкретную точку, составление уравнения движения тела по заданному уравнению скорости или ускорения).
Во второй части пособия разобраны основные задачи темы, а также представлены задания для самостоятельной работы студентов. Предложенные задачи разнообразны по трудности, что дает возможность осуществить индивидуальный подход к студентам, в частности, организовать работу с наиболее подготовленными, проявляющих интерес к математике. Эти задания на закрепление знаний, умений и навыков. Упражнения для самостоятельного решения снабжены ответами.
Особенностью представленного пособия является усиление роли самостоятельной работы студентов.
Изучив, данное пособие студент должен уметь обобщать полученные знания, вычислять интегралы различных функций, находить первообразную функции по начальным данным, выделять из семейства кривых с одинаковым наклоном линии, проходящей через конкретную точку, составлять уравнение движения тела по заданному уравнению скорости или ускорения его движения.
Теоретическая часть
Неопределенный интеграл и его свойства
Первообразная функции
Одной из главных задач дифференцированного исчисления является задача нахождения скорости изменения какой-либо функции, т.е. задача нахождения производной (или дифференциала). На практике часто приходится решать обратную задачу: зная скорость изменения функции, найти эту функцию; эта операция называется интегрированием. Это означает, что необходимо найти функцию 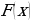 по одному из выражений
по одному из выражений 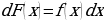 или
или 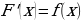 , где
, где 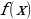 – известная функция.
– известная функция.
Искомая функция 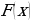 называется первообразной функцией по отношению к функции
называется первообразной функцией по отношению к функции 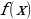 .
.
Определение. Первообразной функцией для данной функции 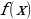 называется такая функция
называется такая функция 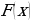 , производная от которой равна
, производная от которой равна 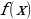 (или, что то же самое, дифференциал которой равен
(или, что то же самое, дифференциал которой равен 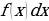 ).
).
Дифференцирование функции – однозначная операция, то есть если функция имеет производную, то только одну. Это утверждение следует из определение предела и производной: если функция имеет предел, то только один. Обратная операция – отыскание первообразной – неоднозначна.
Например, так, функции 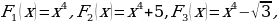
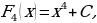 где
где 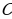 – любое действительное число, являются первообразными функции
– любое действительное число, являются первообразными функции 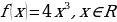 , поскольку все эти функции имеют одну и ту же производную
, поскольку все эти функции имеют одну и ту же производную 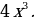
Теорема. Если 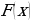 является первообразной функции
является первообразной функции 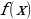 на некотором промежутке, то множество всех первообразных этой функции имеет вид
на некотором промежутке, то множество всех первообразных этой функции имеет вид 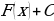 , где
, где 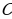 – любое действительное число.
– любое действительное число.
Доказательство.
Пусть 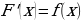 . Тогда
. Тогда 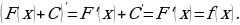
Покажем, что все первообразные функции 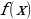 отличаются лишь постоянным слагаемым.
отличаются лишь постоянным слагаемым.
Пусть 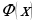 – другая первообразная функции
– другая первообразная функции 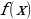 на рассматриваемом промежутке, то есть
на рассматриваемом промежутке, то есть 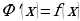 . Тогда
. Тогда 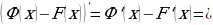
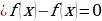 при всех
при всех 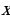 из рассматриваемого промежутка. Следовательно,
из рассматриваемого промежутка. Следовательно, 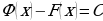 .
.
Что и требовалось доказать.
Таким образом, любые две первообразные данной функции отличаются друг от друга на постоянное слагаемое, а выражение 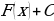 исчерпывает множество всех первообразных заданной функции
исчерпывает множество всех первообразных заданной функции 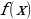 .
.
И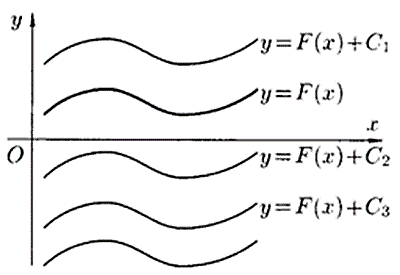 так, задача нахождения первообразной неоднозначна. Она имеет бесконечное множество решений.
так, задача нахождения первообразной неоднозначна. Она имеет бесконечное множество решений.
Геометрически выражение 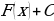 представляет собой семейство кривых, получаемых из любой из них параллельным переносом вдоль оси Ох.
представляет собой семейство кривых, получаемых из любой из них параллельным переносом вдоль оси Ох.
Неопределенный интеграл и его простейшие свойства
Отыскание первообразной функции 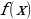 по заданной ее производной
по заданной ее производной 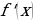 или по дифференциалу
или по дифференциалу 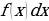 есть действие, обратное дифференцированию, – интегрирование.
есть действие, обратное дифференцированию, – интегрирование.
Определение. Совокупность всех первообразных 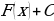 функции
функции 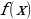 на рассматриваемом промежутке называется неопределенным интегралом и обозначается символом
на рассматриваемом промежутке называется неопределенным интегралом и обозначается символом 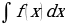 , где
, где 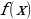 – подынтегральная функция,
– подынтегральная функция, 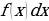 – подынтегральное выражение,
– подынтегральное выражение, 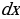 – дифференциал независимой переменной, х – переменная интегрирования.
– дифференциал независимой переменной, х – переменная интегрирования.
Таким образом, если 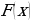 – какая-либо первообразная функции
– какая-либо первообразная функции 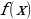 на некотором промежутке, то
на некотором промежутке, то
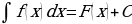 ,
,
где 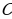 – любое действительное число.
– любое действительное число.
Наличие постоянной 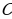 делает задачу нахождения функции по ее производной не вполне определенной; отсюда происходит и само название «неопределенной интеграл».
делает задачу нахождения функции по ее производной не вполне определенной; отсюда происходит и само название «неопределенной интеграл».
Значит, чтобы найти неопределенной интеграл от заданной функции, нужно найти какую-нибудь одну ее первообразную и прибавить к ней произвольную постоянную 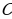 .
.
Слово «интеграл» происходит от латинского слова integer, что означает «восстановленный».
Чтобы проверить, правильно ли найден неопределенный интеграл, необходимо продифференцировать полученную функцию; если при этом получается подынтегральное выражение, то интеграл найден верно.
Неопределенные интегралы можно находить, подбирая первообразные. Однако, это не всегда просто. При интегрировании помогает знание некоторых свойств, формул интегрирования, а также специальных приемов.
Рассмотрим основные свойства неопределенного интеграла.
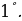 Производная неопределенного интеграла равна подынтегральной функции, то есть
Производная неопределенного интеграла равна подынтегральной функции, то есть
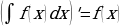 .
.
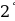 . Постоянный множитель подынтегрального выражения можно вынести за знак неопределенного интеграла, то есть
. Постоянный множитель подынтегрального выражения можно вынести за знак неопределенного интеграла, то есть
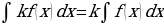 ,
,
где 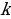 – постоянная, отличная от нуля, величина.
– постоянная, отличная от нуля, величина.
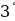 . Неопределенный интеграл от алгебраической суммы функций равен алгебраической сумме неопределенных интегралов от этих функций, то есть
. Неопределенный интеграл от алгебраической суммы функций равен алгебраической сумме неопределенных интегралов от этих функций, то есть
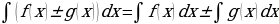 .
.
При интегрировании алгебраической суммы функций принято записывать только одну произвольную постоянную, так как алгебраическая сумма произвольных постоянных есть постоянная.
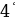 . Дифференциал неопределенного интеграла равен подынтегральному выражению, то есть
. Дифференциал неопределенного интеграла равен подынтегральному выражению, то есть
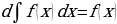 .
.
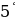 . Неопределенный интеграл от дифференциала (производной) некоторой функции равен сумме этой функции и произвольной постоянной
. Неопределенный интеграл от дифференциала (производной) некоторой функции равен сумме этой функции и произвольной постоянной 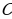 , то есть
, то есть
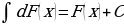 или
или 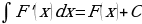 .
.
Данные свойства вытекают непосредственно из определения неопределенного интеграла.
Основные формулы интегрирования.
На основании определения неопределенного интеграла, правил интегрирования и таблицы производных основных элементарных функций можно составить таблицу основных неопределенных интегралов:
Интегралы, приведенные в таблице, называются табличными интегралами.
Методы интегрирования
1.2.1. Метод непосредственного интегрирования
Определение. Непосредственным интегрированием называется вычисление неопределенных интегралов путем приведения их к табличным с применением основных свойств.
Здесь могут представиться следующие случаи:
Данный интеграл находится непосредственно по таблице;
Данный интеграл после применения свойств 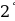 и
и 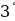 приводится к одному или нескольким табличным интегралам;
приводится к одному или нескольким табличным интегралам;
Данный интеграл после элементарных тождественных преобразований и применения свойств 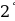 и
и 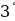 приводится к одному или нескольким табличным интегралам.
приводится к одному или нескольким табличным интегралам.
Интегрирование методом замены переменной
(способ подстановки)
Если заданный интеграл с помощью алгебраических преобразований трудно или невозможно свести к одному или нескольким табличным интегралам, то для его отыскания применяют особые способы, одним из которых является способ подстановки (или замены переменной).
Заметим, что все способы интегрирования имеют целью свести данный интеграл к табличному с помощью тех или иных искусственных преобразований.
Метод замены переменной обычно применяется, когда подынтегральное выражение представляет собой независимую переменную, умноженную на многочлен от этой переменной, или на тригонометрическую функцию от этой переменной или на степенную функцию (в том числе корень) от этой переменной.
Алгоритм вычисления неопределенного интеграла
методом замены переменной
Определите, к какому табличному интегралу приводится данный интеграл (предварительно преобразовав подынтегральное выражение, если нужно);
В интеграле 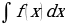 замените переменную х новой переменной t с помощью подстановки:
замените переменную х новой переменной t с помощью подстановки:
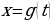 ;
;
Найдите дифференциалы обеих частей подстановки:
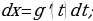
Произведите замену под интегралом:
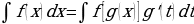 ;
;
Найдите полученный интеграл относительно новой переменной t: 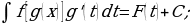
В результате произведите обратную замену, то есть перейдите к старой переменной х.
Интегрирование по частям
При интегрировании функций, содержащих произведения, логарифмические, показательные, тригонометрические, обратные тригонометрические функции, а также их комбинации бывает удобно воспользоваться способом интегрирования по частям, который позволяет свести исходный неопределенный интеграл к более простому виду либо к табличному интегралу.
Метод вычисления интегралов, называемый интегрированием по частям, основан на правиле дифференцирования произведения.
Выведем формулу интегрирования по частям.
Интегрируя обе части равенства 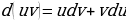 , получим
, получим
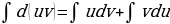 или
или 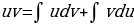 ,
,
откуда
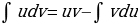 .
.
С помощью этой формулы нахождение интеграла 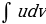 сводится к нахождению интеграла
сводится к нахождению интеграла 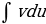 , который может оказаться или проще данного, или даже табличным.
, который может оказаться или проще данного, или даже табличным.
При использовании формулы интегрирования по частям данное подынтегральное выражение представляют в виде произведения двух сомножителей, которые обозначаются u и dv. Множитель u выбирают так, чтобы u было проще чем u.
было проще чем u.
Алгоритм вычисления неопределенного интеграла
по частям
Выберите функцию u (от исходной переменной) такую, что дифференциал от нее 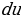 проще, чем u;
проще, чем u;
Разделите подынтегральное выражение на u – получите dv (можно устно);
Из dv найдите интегрированием v (обычно ее находят устно и сразу вносят под знак дифференциала, но можно и отдельным интегрированием);
Из u найдите его дифференциал 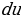 ;
;
Подставьте полученные величины 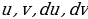 в формулу
в формулу 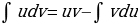 ;
;
Возьмите интеграл от 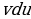 . При этом возможны варианты:
. При этом возможны варианты:
если интеграл от 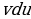 легкий, то взять его;
легкий, то взять его;
если интеграл от 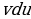 все еще не простой, но проще исходного, применить интегрирование по частям уже для него;
все еще не простой, но проще исходного, применить интегрирование по частям уже для него;
если в правой части получился такой же интеграл, как и исходный, в этом уравнении можно привести подобные и результат получится сам собой;
если интеграл от 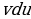 сложнее взять, повторить шаги – 6 для другого
сложнее взять, повторить шаги – 6 для другого 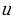 .
.
Самое сложное, что есть в этом методе – это правильно определить, какую часть подынтегрального выражения следует брать за u, а какую за 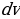 .
.
В частности, полезно иметь в виду, что в интегралах вида 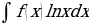 ;
; 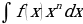 ;
; 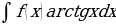 ;
; 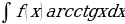 ;
; 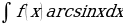 в большинстве случаев функцию
в большинстве случаев функцию 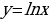 ;
; 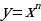 ;
; 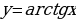 ;
; 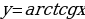 ;
; 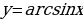 принимают за функцию u. А в интегралах вида
принимают за функцию u. А в интегралах вида 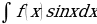 ;
; 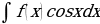 ;
; 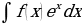 за функцию u принимают функцию
за функцию u принимают функцию 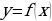 .
.
Интегрирование рациональных дробей
Определение. Любое выражение вида 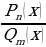 , где
, где 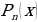 и
и 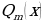 – многочлены соответственно n-ой и m-ой степени называют рациональной дробью.
– многочлены соответственно n-ой и m-ой степени называют рациональной дробью.
Если 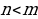 , то рациональная дробь правильная, если
, то рациональная дробь правильная, если 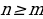 , то рациональная дробь неправильная.
, то рациональная дробь неправильная.
Любую неправильную дробь можно представить в виде суммы многочлена (целой части) и правильной дроби (дробной части), поэтому интегрирование рациональных дробей сводится к интегрированию правильных рациональных дробей.
Для интегрирования правильной рациональной дроби ее представляют в виде суммы простейших дробей вида 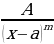 и
и 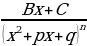 , где
, где 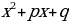
не имеет действительных корней, а 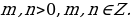
Алгоритм интегрирования рациональных дробей
Выясните является ли дробь правильной? Данный шаг выполняется устно;
Если дробь неправильная преобразуйте ее в правильную, выделив целое выражение;
. Разложите знаменатель на множители;
Методом неопределенных коэффициентов разложите подынтегральную функцию в сумму простейших (элементарных) дробей;
Определите коэффициенты;
Вычислите интегралы от простейших дробей.
1.2.5. Интегрирование некоторых тригонометрических функций
1. Интегралы вида 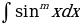 и
и 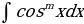 находят в зависимости от четности степени
находят в зависимости от четности степени 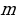 :
:
а) если 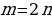 , то есть
, то есть 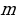 – четное, то используют формулы понижения степени:
– четное, то используют формулы понижения степени:
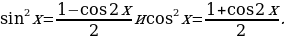
Б) если 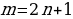 , то есть
, то есть 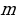 – нечетное, то нужно отделить от нечетной степени один множитель и ввести новую переменную, пологая
– нечетное, то нужно отделить от нечетной степени один множитель и ввести новую переменную, пологая 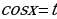 или
или 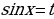 .
.
2. Интегралы вида 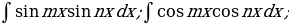
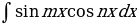 вычисляют с помощью преобразований подынтегральной функции по следующим формулам:
вычисляют с помощью преобразований подынтегральной функции по следующим формулам:
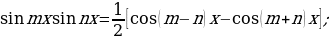
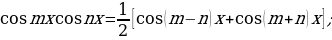
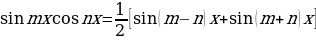
Приложения неопределенного интеграла
1.3.1. Нахождение первообразной по начальным условиям
Известно, что при интегрировании функции получается совокупность первообразных. Для выделения из всей совокупности конкретной первообразной задают дополнительные, так называемые начальные условия.
При решении таких задач используют следующий алгоритм:
Алгоритм нахождение первообразной по начальным условиям
Находят неопределенный интеграл от заданной функции;
Вычисляют величину С, подставляя начальные условия в полученную совокупность первообразных для заданной функции;
Находят искомую первообразную, заменяя в совокупности первообразных постоянную интегрирования ее вычисленным значением.
Выделение из семейства кривых с одинаковым наклоном линии, проходящей через конкретную точку
Под наклоном кривой понимают тангенс угла наклона касательной к этой кривой в данной точке.
Из дифференциального исчисления известно, что угловой коэффициент касательной k кривой 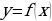 в точке с абсциссой х равен значению производной в этой точке, то есть
в точке с абсциссой х равен значению производной в этой точке, то есть 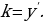
Рассмотрим обратную задачу: зная наклон 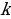 кривой в любой ее точке как функцию абсциссы этой точки, то есть, зная, что
кривой в любой ее точке как функцию абсциссы этой точки, то есть, зная, что 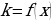 , найти уравнение кривой.
, найти уравнение кривой.
Так как 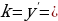
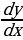 , то
, то 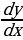 =
=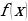 , то есть
, то есть 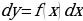 , откуда интегрированием находим
, откуда интегрированием находим 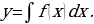 Вычислив этот неопределенный интеграл, получим уравнение
Вычислив этот неопределенный интеграл, получим уравнение 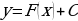 , содержащее произвольную постоянную С. Этому уравнению на плоскости соответствует бесконечное множество кривых (семейство кривых), уравнения которых отличаются друг от друга только постоянными слагаемыми.
, содержащее произвольную постоянную С. Этому уравнению на плоскости соответствует бесконечное множество кривых (семейство кривых), уравнения которых отличаются друг от друга только постоянными слагаемыми.
Определение. Графики функций, которые получаются в результате интегрирования называются интегральными кривыми.
К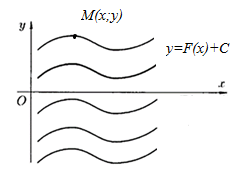 аждый интеграл дает семейство интегральных кривых. Интегральные кривые одного семейства имеют одну и ту же форму и смещены друг относительно друга вдоль оси Оу. Сдвиг кривой определяется постоянной С. Из семейства кривых, имеющих один и тот же наклон, выделяют ту, которая проходит через данную точку.
аждый интеграл дает семейство интегральных кривых. Интегральные кривые одного семейства имеют одну и ту же форму и смещены друг относительно друга вдоль оси Оу. Сдвиг кривой определяется постоянной С. Из семейства кривых, имеющих один и тот же наклон, выделяют ту, которая проходит через данную точку.
Составление уравнения движения тела по заданному уравнению скорости или ускорения
Из дифференциального исчисления известно, что 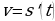 и
и 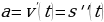 , где
, где 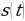 ,
, 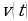 и
и 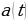 – соответственно путь, скорость и ускорение движущегося тела. Тогда закон движения тела по заданной скорости можно найти интегрированием, а по заданному ускорению – двукратным интегрированием.
– соответственно путь, скорость и ускорение движущегося тела. Тогда закон движения тела по заданной скорости можно найти интегрированием, а по заданному ускорению – двукратным интегрированием.
Практическая часть
2.1. Примеры решения задач
1. Найдите первообразную функции 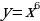 на множестве R.
на множестве R.
Решение: Степень 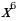 получается при дифференцировании
получается при дифференцировании 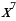 . Так как
. Так как 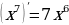 , то, чтобы при дифференцировании
, то, чтобы при дифференцировании 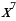 получить перед
получить перед 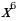 коэффициент 1, нужно
коэффициент 1, нужно 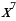 взять с коэффициентом
взять с коэффициентом 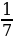 . Следовательно,
. Следовательно, 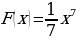 .
.
2. Показать, что функция 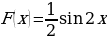 является первообразной функции
является первообразной функции 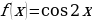 .
.
Решение: Так как 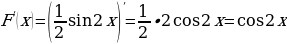 , то
, то 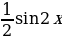 – первообразная функции
– первообразная функции 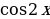 .
.
3. Найдите интегралы
1) 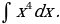
Решение: Применяя формулу 2 при 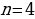 , получим
, получим
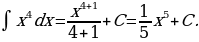
2) 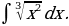
Решение: 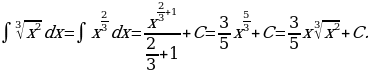
3) 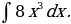
Решение: Применяя формулу 2 и свойство 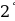 , получим
, получим 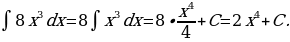
4) 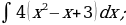
Решение: Применяя формулу 2 и свойства 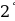 и
и 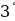 , получим
, получим
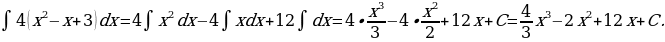
Постоянная интегрирования 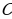 равна алгебраической сумме трех постоянных интегрирования, так как каждый интеграл имеет свою произвольную постоянную интегрирования (
равна алгебраической сумме трех постоянных интегрирования, так как каждый интеграл имеет свою произвольную постоянную интегрирования (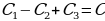 ).
).
5) 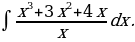
Решение: 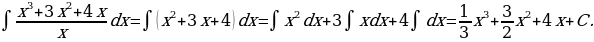
6) 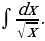
Решение: 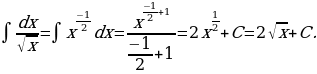
7) 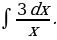
Решение: По формуле 3 находим 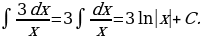
8) 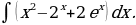
Решение: По формулам 2, 4, 5 и свойствам 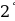 и
и 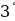 находим
находим 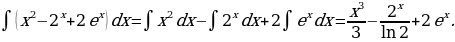
9) 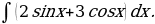
Решение: Применяя формулы 6 и 8 и свойства 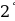 и
и 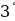 , получим
, получим 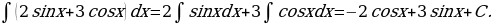
10) 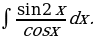
Решение: Применяя формулу 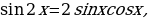 получим
получим 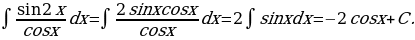
11) 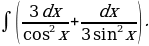
Решение: По свойствам 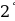 и
и  , применяя формулы 8 и 9, получим
, применяя формулы 8 и 9, получим 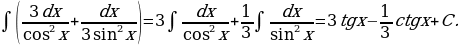
12) 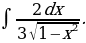
Решение: Применяя формулу 12 и свойство  , находим
, находим 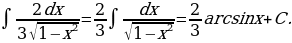
13) 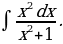
Решение: Имеем 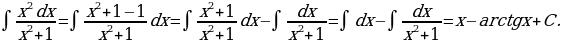
Здесь мы преобразовали числитель: 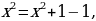 а затем использовали свойство
а затем использовали свойство 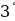 и формулы 1 и 13.
и формулы 1 и 13.
14) 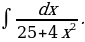
Решение: Имеем 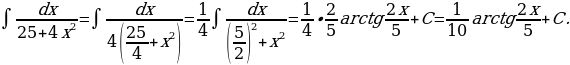
15) 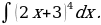
Решение: Введем подстановку 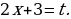 Дифференцируя, имеем
Дифференцируя, имеем 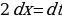 , откуда
, откуда 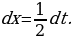 Подставив в данный интеграл вместо
Подставив в данный интеграл вместо 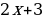 и
и 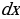 их выражения, получим
их выражения, получим 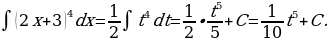
Заменив 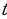 его выражением через
его выражением через 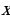 , находим
, находим 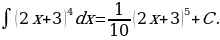
Решение этого примера можно кратко оформить так:
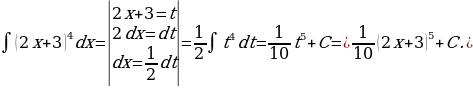
16) 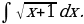
Решение: 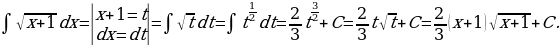
17) 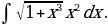
Решение: 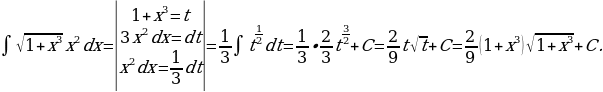
18) 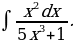
Решение: 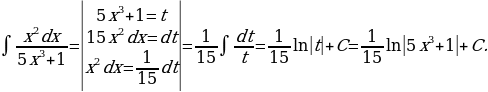
19) 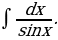
Решение: Так как 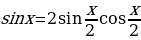 , то
, то 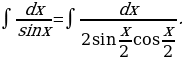 Разделив и умножив знаменатель на
Разделив и умножив знаменатель на 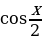 , получим
, получим 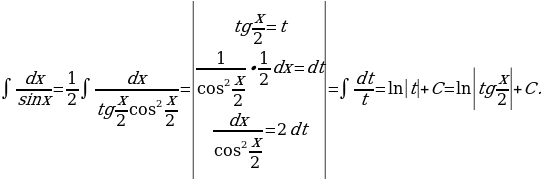
20) 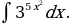
Решение: 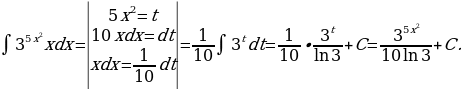
21) 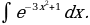
Решение: 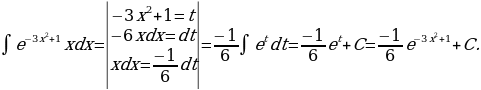
22) 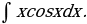
Решение: Интеграл содержит произведение двух функций 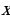 и
и 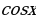 . Способ подстановки не дает возможности найти этот интеграл. Обозначим
. Способ подстановки не дает возможности найти этот интеграл. Обозначим 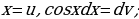 тогда
тогда 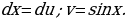 Приняв
Приняв 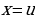 , мы получили
, мы получили 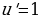 и интеграл
и интеграл 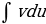 оказался проще, чем
оказался проще, чем 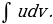 Далее необходимо применить формулу интегрирования по частям.
Далее необходимо применить формулу интегрирования по частям.
Решение этого примера можно кратко оформить так:
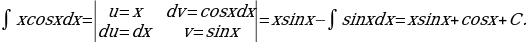
Если же в этом интеграле сделать другую замену: 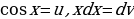 , то полученный интеграл окажется сложнее исходного, то есть замена окажется неудачной.
, то полученный интеграл окажется сложнее исходного, то есть замена окажется неудачной.
Умение определить целесообразность той или иной замены приходит с приобретением навыка.
23) 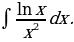
Решение: 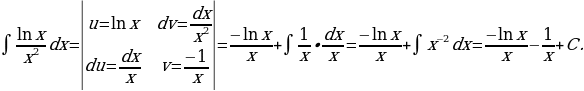
24) 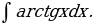
Решение: 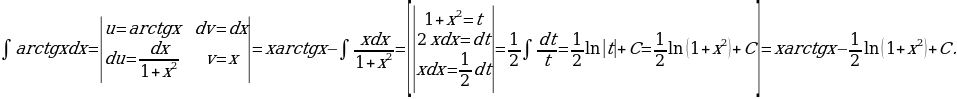
25) 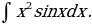
Решение: Иногда формулу интегрирования по частям приходится дважды.
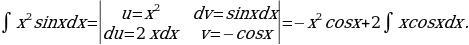
Для нахождения полученного в правой части равенства интеграла снова интегрируем по частям:
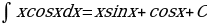 (см. решение примера 22).
(см. решение примера 22).
В результате получаем окончательный ответ:
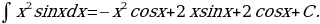
26) 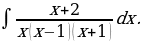
Решение: Разложим дробь 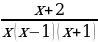 на сумму трех дробей:
на сумму трех дробей:
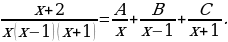
Приведя к общему знаменателю, получим тождество:
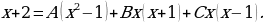
Корни знаменателя: 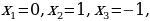 следовательно,
следовательно,
| 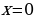 , ,
| тогда 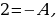 | или 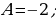 |
| 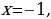
| тогда 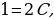 | или 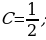 |
| 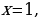
| тогда 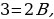 | или 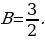 |
Следовательно, 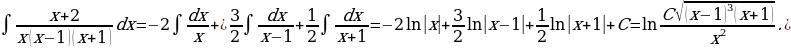
27) 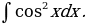
Решение: 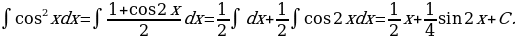
28) 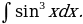
Решение: 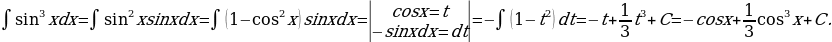
29) 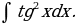
Решение: 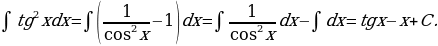
30) 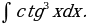
Решение: 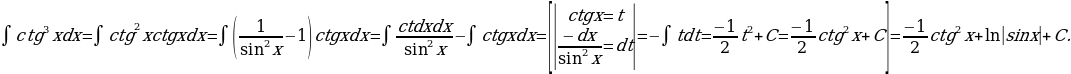
31) 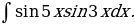
Решение: 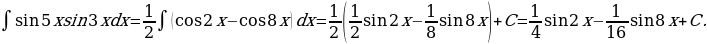
32) 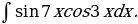
Решение: 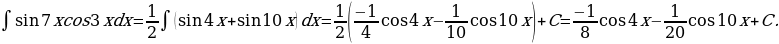
4. Найдите функцию, производная которой равна 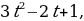 если известно, что при
если известно, что при 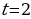 функция принимает значение, равное 25.
функция принимает значение, равное 25.
Решение: 1) Из условия следует, что искомая функция является первообразной функции 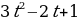 ; поэтому, взяв неопределенный интеграл от
; поэтому, взяв неопределенный интеграл от 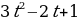 , найдем все первообразные указанной функции:
, найдем все первообразные указанной функции: 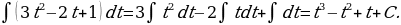
2) Из полученного выражения 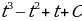 , определяющие все первообразные функции
, определяющие все первообразные функции 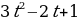 , найдем теперь искомую первообразную функции. Используя дополнительное условие (значение искомой функции равно 25 при
, найдем теперь искомую первообразную функции. Используя дополнительное условие (значение искомой функции равно 25 при 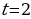 ), найдем определенное значение постоянной интегрирования
), найдем определенное значение постоянной интегрирования 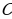 ; имеем
; имеем 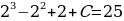 , откуда
, откуда 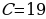 .
.
3) Итак, искомая функция имеет вид 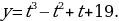
5. Составить уравнение кривой, проходящей через точку 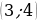 , если угловой коэффициент касательной к этой кривой в любой ее точке
, если угловой коэффициент касательной к этой кривой в любой ее точке 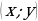 равен
равен 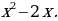
Решение: 1) Известно, что 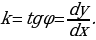
В данном случае имеем 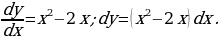
В результате интегрирования получаем 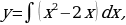 т.е.
т.е.
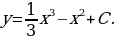
2) Теперь из найденного семейства кривых выделим ту кривую, которая проходит через данную точку 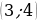 . Для этого подставим в уравнение
. Для этого подставим в уравнение 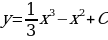 вместо
вместо 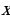 и
и 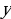 координаты данной точки. Имеем
координаты данной точки. Имеем 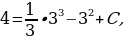 т.е.
т.е. 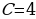 .
.
3) Через данную точку проходит та из семейства кривых
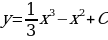 , для которой
, для которой 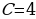 , т.е.
, т.е. 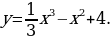
6. Скорость прямолинейного движения точки задана уравнением
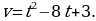 Найдите уравнение движения точки.
Найдите уравнение движения точки.
Решение: 1) Известно, что скорость прямолинейного движения тела равна производной пути 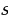 по времени
по времени 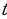 , т.е.
, т.е. 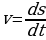 , откуда
, откуда 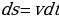 . Тогда имеем
. Тогда имеем 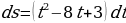 .
.
2) Чтобы найти уравнение движения, проинтегрируем обе части полученного равенства: 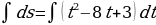 , следовательно
, следовательно
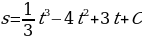 . Это искомое уравнение.
. Это искомое уравнение.
7. Скорость прямолинейного движения точки изменяется по закону
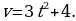 Найдите закон движения
Найдите закон движения 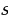 , если за время
, если за время 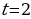 с точка прошла 20 м.
с точка прошла 20 м.
Решение: 1) Имеем 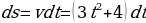 ; тогда
; тогда
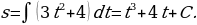
2) Подставив в найденное уравнение начальные условия 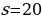 м,
м,
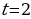 с, получим
с, получим 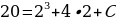 , т.е.
, т.е. 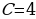 .
.
3) Итак, искомое уравнение имеет вид 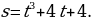
8. Найти закон движения свободно падающего тела при постоянном ускорении 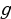 , если в начальный момент движения тело находилось в покое.
, если в начальный момент движения тело находилось в покое.
Решение: 1) Известно, что ускорение прямолинейно движущегося тела есть производная скорости 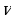 по времени
по времени 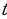 . Следовательно,
. Следовательно, 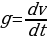 , откуда
, откуда 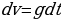 . Откуда после интегрирования находим
. Откуда после интегрирования находим
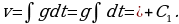
2) Используя начальные условия 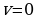 при
при 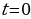 , находим
, находим 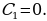
3) Таким образом, уравнение скорости движения имеет вид 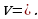
4) Теперь воспользуемся тем, что скорость прямолинейного движения тела равна производной пути 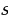 по времени
по времени 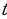 , т.е.
, т.е. 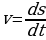 . Так как
. Так как 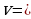 , то
, то 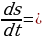 или
или 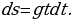 Интегрируя, находим
Интегрируя, находим 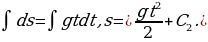
5) Используя начальные условия 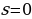 при
при 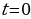 , находим
, находим 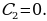
6) Итак, уравнение движения свободно падающего тела имеет вид
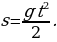
9. Тело движется с ускорением 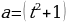 м/с2. Найдите закон движения
м/с2. Найдите закон движения 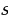 , если за время
, если за время 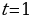 с скорость
с скорость 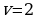 м/с, а путь
м/с, а путь 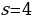 м.
м.
Решение: Эта задача также решается в два этапа. Сначала нужно найти 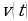 , зная, что
, зная, что 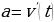 . Затем найти
. Затем найти 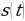 , зная, что
, зная, что 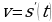 .
.
Имеем 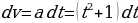 , откуда
, откуда
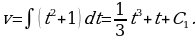
2) Используя начальные условия 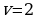 при
при 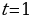 , получим
, получим
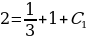 , откуда
, откуда 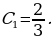
3) Следовательно, 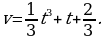
4) Имеем 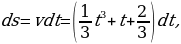 откуда
откуда
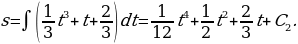
5) Используя начальные условия 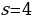 при
при 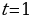 , получим
, получим
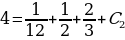 , откуда находим
, откуда находим 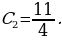
6) Итак, 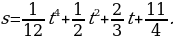
2.2. Задачи для самостоятельного решения
1. Найдите первообразную функции 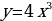 на множестве R.
на множестве R.
2. Проверить, что функция 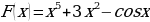 является первообразной функции
является первообразной функции 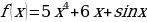 на множестве R.
на множестве R.
3. Показать, что функция 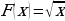 есть первообразная функции
есть первообразная функции 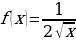 на промежутке
на промежутке 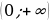 .
.
4. Даны пары функций, из которых вторая должна быть первообразной для первой: а) 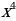 и
и 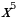 ; б)
; б) 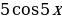 и
и 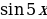 ; в)
; в) 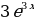 и
и 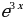 ; г)
; г) 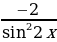 и
и 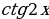 ;
;
д) 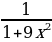 и
и 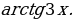 В каких примерах допущены ошибки?
В каких примерах допущены ошибки?
5. Найти интегралы
| 1) 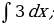 |
| 11) 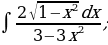 |
| 21) 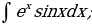 |
| 2) 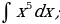 |
| 12) 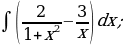 |
| 22) 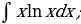 |
| 3) 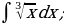 |
| 13) 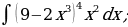 |
| 23) 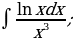 |
| 4) 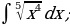 |
| 14) 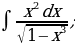 |
| 24) 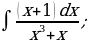 |
| 5) 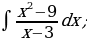 |
| 15) 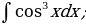 |
| 25) 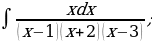 |
| 6) 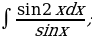 |
| 16) 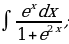 |
| 26) 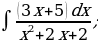 |
| 7) 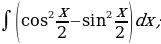 |
| 17) 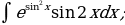 |
| 27) 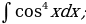 |
| 8) 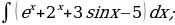 |
| 18) 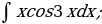 |
| 28) 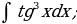 |
| 9) 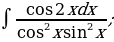 |
| 19) 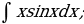 |
| 29) 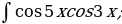 |
| 10) 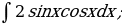 |
| 20) 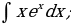 |
| 30) 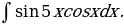 |
6. Найдите функцию, обращающуюся в нуль при 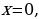 если производная этой функции имеет вид
если производная этой функции имеет вид 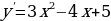 .
.
7. Найдите 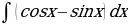 , если при
, если при 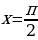 первообразная равна 6.
первообразная равна 6.
8. Найдите уравнение кривой, проходящей через точку 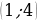 , если угловой коэффициент касательной в каждой точке кривой задается функцией
, если угловой коэффициент касательной в каждой точке кривой задается функцией 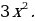
9. На промежутке 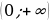 найдите такую первообразную функции
найдите такую первообразную функции 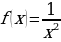 , график которой проходит через точку
, график которой проходит через точку 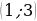 .
.
10. Составьте уравнение кривой, проходящей через точку 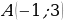 , если угловой коэффициент касательной к кривой в каждой точке кривой равен утроенному квадрату абсциссы точки касания.
, если угловой коэффициент касательной к кривой в каждой точке кривой равен утроенному квадрату абсциссы точки касания.
11. Найдите уравнение кривой, проходящей через точку 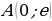 , если угловой коэффициент касательной к кривой в любой ее точке кривой равен
, если угловой коэффициент касательной к кривой в любой ее точке кривой равен 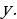
12. Скорость тела задана уравнением 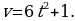 Найти уравнение движения, если за время
Найти уравнение движения, если за время 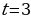 с тело прошло путь
с тело прошло путь 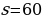 м.
м.
13. Точка движется с ускорением 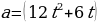 м/с2. Найдите закон движения точки
м/с2. Найдите закон движения точки 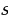 , если в момент времени
, если в момент времени 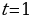 ее скорость
ее скорость 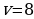 м/с, а путь
м/с, а путь 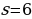 м.
м.
Ответы
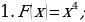 4. Ошибки допущены в примерах а) и д); 5. 1)
4. Ошибки допущены в примерах а) и д); 5. 1) 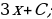 2)
2) 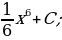 3)
3) 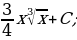 4)
4) 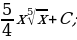 5)
5) 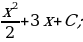 6)
6) 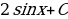 ; 7)
; 7) 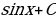 ; 8)
; 8) 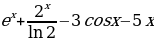 ; 9)
; 9) 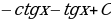 ; 10)
; 10) 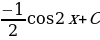 ; 11)
; 11) 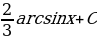 ; 12)
; 12) 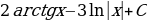 ; 13)
; 13) 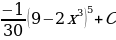 ; 14)
; 14) 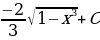 ; 15)
; 15) 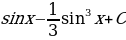 ; 16)
; 16) 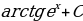 ; 17)
; 17) 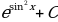 ; 18)
; 18) 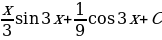 ; 19)
; 19) 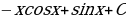 ; 20)
; 20) 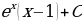 ; 21)
; 21) 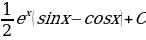 ; 22)
; 22) 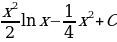 ; 23)
; 23) 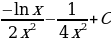 ;24)
;24) 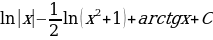 ; 25)
; 25) 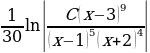 ; 26)
; 26) 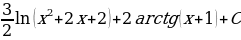 ; 27)
; 27) 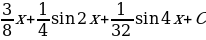 ; 28)
; 28) 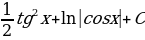 ; 29)
; 29) 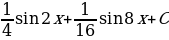 ; 30)
; 30) 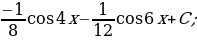 6.
6. 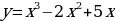 ; 7.
; 7. 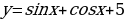 ; 8.
; 8. 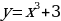 ; 9.
; 9. 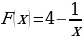 ; 10.
; 10. 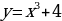 ; 11.
; 11. 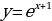 ; 12.
; 12. 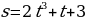 ; 13.
; 13. 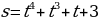 .
.
Список литературы
Богомолов Н.В. Практические занятия по математике: Учебное пособие для средних проф. учеб. заведений – М.: Высш. шк. 2007.
Клюева Л.А., Тальский Д.А. Практикум по математике для заочных техникумов. Учеб. пособие. – М.: Высш. шк. 1970.
Лисичкин В.Т., Соловейчик И.Л. Математика: Учеб. пособие для техникумов. – М.: Высш. шк. 2013.
Михайлова Ж.Н. Алгоритмы – ключ к решению задач по алгебре 10 – 11 классы. – М. Просвещение, 2009.
Сергиенко Л.Ю., Самойленко П.И. Планирование учебного процесса по математике: Учеб.-метод. Пособие для преподавателей сред. спец. учеб. заведений. – М.: Высш. шк. 2014.
http://www.mathprofi.ru/integraly_primery_reshenij.html
http://www.xn--80aaenbrolc2dd.xn--p1ai/neopredelennyj-integral-primery-reshenij/
http://festival.1september.ru/articles/606369/







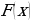 по одному из выражений
по одному из выражений 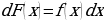 или
или 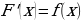 , где
, где 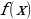 – известная функция.
– известная функция.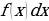 ).
).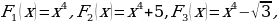
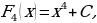 где
где 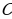 – любое действительное число, являются первообразными функции
– любое действительное число, являются первообразными функции 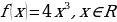 , поскольку все эти функции имеют одну и ту же производную
, поскольку все эти функции имеют одну и ту же производную 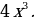
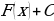 , где
, где 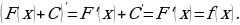
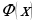 – другая первообразная функции
– другая первообразная функции 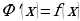 . Тогда
. Тогда 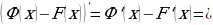
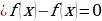 при всех
при всех 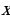 из рассматриваемого промежутка. Следовательно,
из рассматриваемого промежутка. Следовательно, 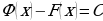 .
. так, задача нахождения первообразной неоднозначна. Она имеет бесконечное множество решений.
так, задача нахождения первообразной неоднозначна. Она имеет бесконечное множество решений.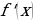 или по дифференциалу
или по дифференциалу 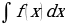 , где
, где 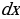 – дифференциал независимой переменной, х – переменная интегрирования.
– дифференциал независимой переменной, х – переменная интегрирования.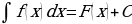 ,
,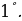 Производная неопределенного интеграла равна подынтегральной функции, то есть
Производная неопределенного интеграла равна подынтегральной функции, то есть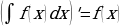 .
.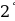 . Постоянный множитель подынтегрального выражения можно вынести за знак неопределенного интеграла, то есть
. Постоянный множитель подынтегрального выражения можно вынести за знак неопределенного интеграла, то есть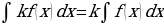 ,
, 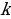 – постоянная, отличная от нуля, величина.
– постоянная, отличная от нуля, величина.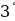 . Неопределенный интеграл от алгебраической суммы функций равен алгебраической сумме неопределенных интегралов от этих функций, то есть
. Неопределенный интеграл от алгебраической суммы функций равен алгебраической сумме неопределенных интегралов от этих функций, то есть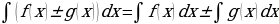 .
.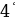 . Дифференциал неопределенного интеграла равен подынтегральному выражению, то есть
. Дифференциал неопределенного интеграла равен подынтегральному выражению, то есть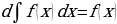 .
.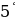 . Неопределенный интеграл от дифференциала (производной) некоторой функции равен сумме этой функции и произвольной постоянной
. Неопределенный интеграл от дифференциала (производной) некоторой функции равен сумме этой функции и произвольной постоянной 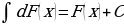 или
или 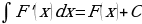 .
.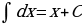
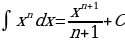

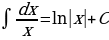
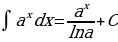
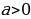 ,
, 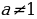
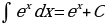
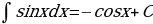
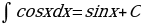
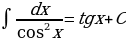
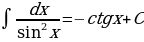
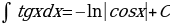
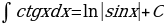
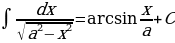
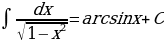
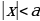 ,
, 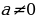
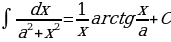
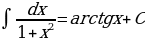
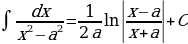
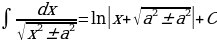
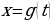 ;
;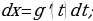
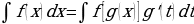 ;
;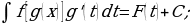
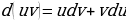 , получим
, получим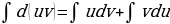 или
или 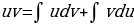 ,
,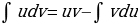 .
.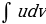 сводится к нахождению интеграла
сводится к нахождению интеграла 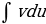 , который может оказаться или проще данного, или даже табличным.
, который может оказаться или проще данного, или даже табличным. было проще чем u.
было проще чем u.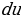 проще, чем u;
проще, чем u;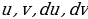 в формулу
в формулу 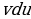 . При этом возможны варианты:
. При этом возможны варианты: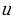 .
.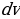 .
.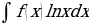 ;
; 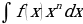 ;
; 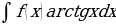 ;
; 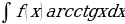 ;
; 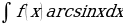 в большинстве случаев функцию
в большинстве случаев функцию 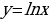 ;
; 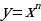 ;
; 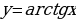 ;
; 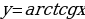 ;
; 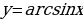 принимают за функцию u. А в интегралах вида
принимают за функцию u. А в интегралах вида 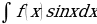 ;
; 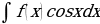 ;
; 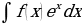 за функцию u принимают функцию
за функцию u принимают функцию 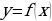 .
.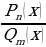 , где
, где 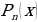 и
и 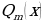 – многочлены соответственно n-ой и m-ой степени называют рациональной дробью.
– многочлены соответственно n-ой и m-ой степени называют рациональной дробью.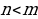 , то рациональная дробь правильная, если
, то рациональная дробь правильная, если 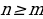 , то рациональная дробь неправильная.
, то рациональная дробь неправильная.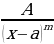 и
и 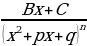 , где
, где 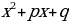
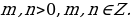
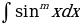 и
и 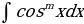 находят в зависимости от четности степени
находят в зависимости от четности степени 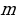 :
: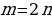 , то есть
, то есть 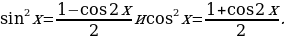
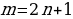 , то есть
, то есть 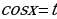 или
или 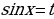 .
.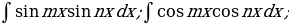
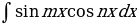 вычисляют с помощью преобразований подынтегральной функции по следующим формулам:
вычисляют с помощью преобразований подынтегральной функции по следующим формулам: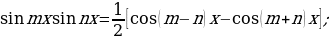
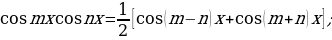
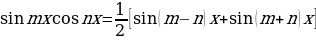
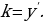
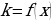 , найти уравнение кривой.
, найти уравнение кривой.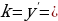
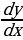 , то
, то 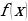 , то есть
, то есть 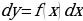 , откуда интегрированием находим
, откуда интегрированием находим 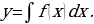 Вычислив этот неопределенный интеграл, получим уравнение
Вычислив этот неопределенный интеграл, получим уравнение 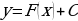 , содержащее произвольную постоянную С. Этому уравнению на плоскости соответствует бесконечное множество кривых (семейство кривых), уравнения которых отличаются друг от друга только постоянными слагаемыми.
, содержащее произвольную постоянную С. Этому уравнению на плоскости соответствует бесконечное множество кривых (семейство кривых), уравнения которых отличаются друг от друга только постоянными слагаемыми. аждый интеграл дает семейство интегральных кривых. Интегральные кривые одного семейства имеют одну и ту же форму и смещены друг относительно друга вдоль оси Оу. Сдвиг кривой определяется постоянной С. Из семейства кривых, имеющих один и тот же наклон, выделяют ту, которая проходит через данную точку.
аждый интеграл дает семейство интегральных кривых. Интегральные кривые одного семейства имеют одну и ту же форму и смещены друг относительно друга вдоль оси Оу. Сдвиг кривой определяется постоянной С. Из семейства кривых, имеющих один и тот же наклон, выделяют ту, которая проходит через данную точку.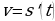 и
и 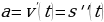 , где
, где 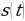 ,
, 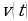 и
и 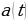 – соответственно путь, скорость и ускорение движущегося тела. Тогда закон движения тела по заданной скорости можно найти интегрированием, а по заданному ускорению – двукратным интегрированием.
– соответственно путь, скорость и ускорение движущегося тела. Тогда закон движения тела по заданной скорости можно найти интегрированием, а по заданному ускорению – двукратным интегрированием. 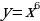 на множестве R.
на множестве R.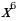 получается при дифференцировании
получается при дифференцировании 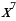 . Так как
. Так как 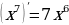 , то, чтобы при дифференцировании
, то, чтобы при дифференцировании 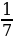 . Следовательно,
. Следовательно, 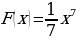 .
. 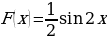 является первообразной функции
является первообразной функции 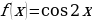 .
.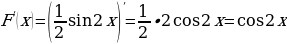 , то
, то 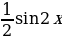 – первообразная функции
– первообразная функции 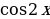 .
. 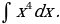
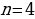 , получим
, получим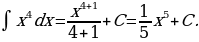
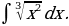
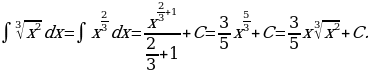
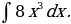
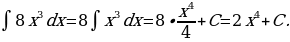
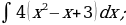
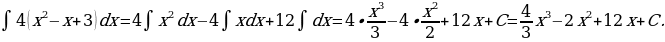
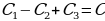 ).
).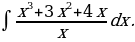
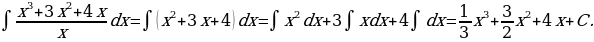
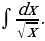
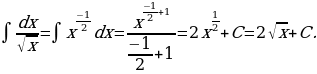
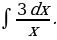
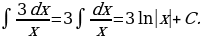
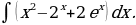
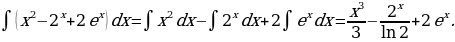
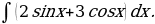
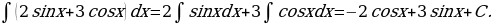
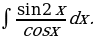
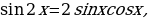 получим
получим 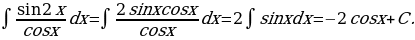
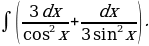
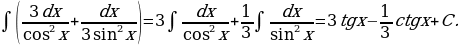
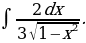
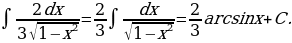
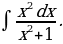
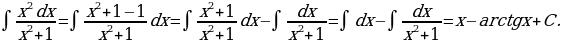
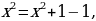 а затем использовали свойство
а затем использовали свойство 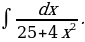
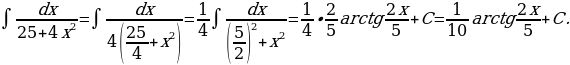
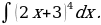
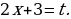 Дифференцируя, имеем
Дифференцируя, имеем 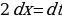 , откуда
, откуда 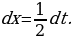 Подставив в данный интеграл вместо
Подставив в данный интеграл вместо 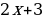 и
и 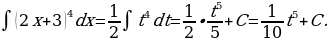
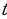 его выражением через
его выражением через 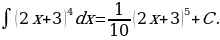
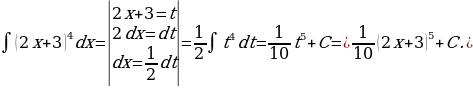
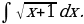
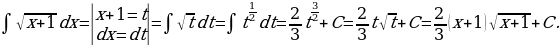
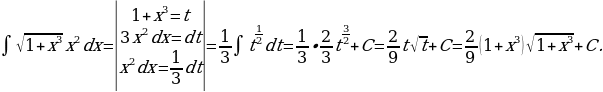
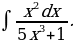
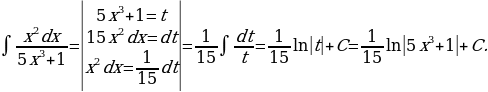
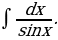
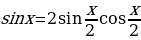 , то
, то 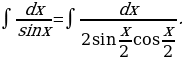 Разделив и умножив знаменатель на
Разделив и умножив знаменатель на 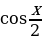 , получим
, получим 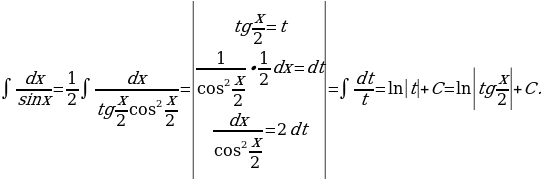
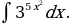
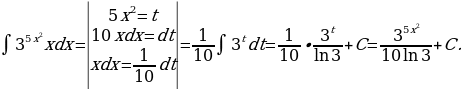
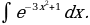
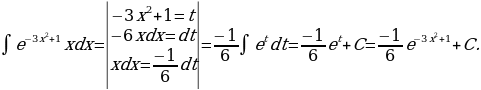
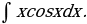
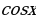 . Способ подстановки не дает возможности найти этот интеграл. Обозначим
. Способ подстановки не дает возможности найти этот интеграл. Обозначим 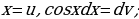 тогда
тогда 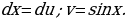 Приняв
Приняв 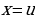 , мы получили
, мы получили 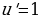 и интеграл
и интеграл 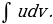 Далее необходимо применить формулу интегрирования по частям.
Далее необходимо применить формулу интегрирования по частям.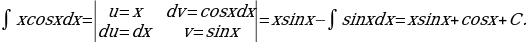
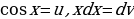 , то полученный интеграл окажется сложнее исходного, то есть замена окажется неудачной.
, то полученный интеграл окажется сложнее исходного, то есть замена окажется неудачной.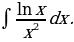
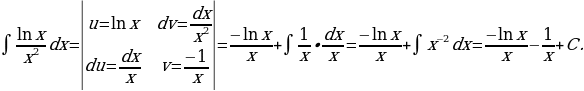
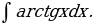
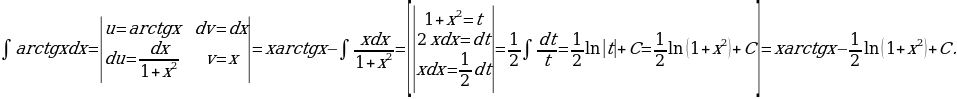
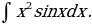
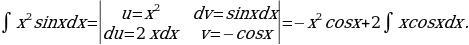
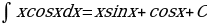 (см. решение примера 22).
(см. решение примера 22).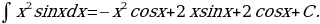
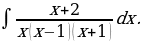
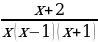 на сумму трех дробей:
на сумму трех дробей: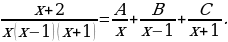
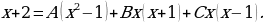
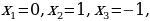 следовательно,
следовательно,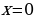 ,
,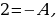
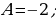
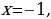
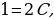
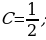
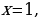
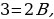
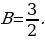
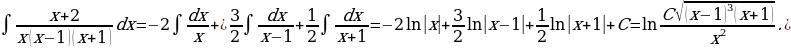
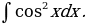
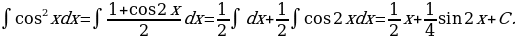
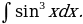
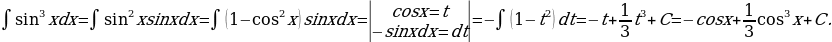
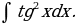
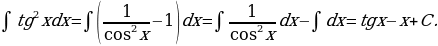
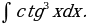
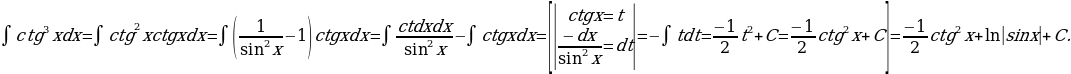
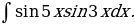
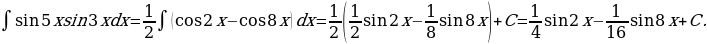
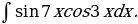
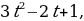 если известно, что при
если известно, что при 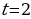 функция принимает значение, равное 25.
функция принимает значение, равное 25.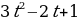 ; поэтому, взяв неопределенный интеграл от
; поэтому, взяв неопределенный интеграл от 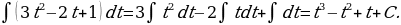
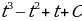 , определяющие все первообразные функции
, определяющие все первообразные функции 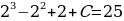 , откуда
, откуда 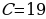 .
.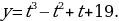
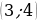 , если угловой коэффициент касательной к этой кривой в любой ее точке
, если угловой коэффициент касательной к этой кривой в любой ее точке 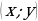 равен
равен 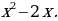
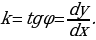
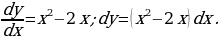
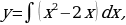 т.е.
т.е. 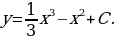
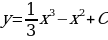 вместо
вместо 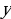 координаты данной точки. Имеем
координаты данной точки. Имеем 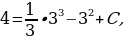 т.е.
т.е. 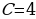 .
.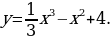
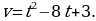 Найдите уравнение движения точки.
Найдите уравнение движения точки.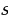 по времени
по времени 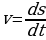 , откуда
, откуда 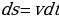 . Тогда имеем
. Тогда имеем 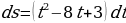 .
.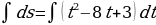 , следовательно
, следовательно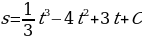 . Это искомое уравнение.
. Это искомое уравнение.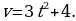 Найдите закон движения
Найдите закон движения 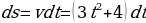 ; тогда
; тогда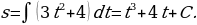
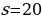 м,
м,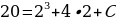 , т.е.
, т.е. 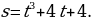
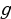 , если в начальный момент движения тело находилось в покое.
, если в начальный момент движения тело находилось в покое.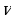 по времени
по времени 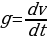 , откуда
, откуда 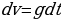 . Откуда после интегрирования находим
. Откуда после интегрирования находим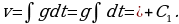
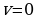 при
при 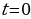 , находим
, находим 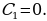
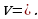
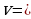 , то
, то 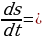 или
или 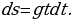 Интегрируя, находим
Интегрируя, находим 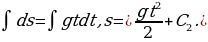
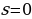 при
при 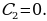
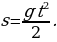
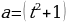 м/с2. Найдите закон движения
м/с2. Найдите закон движения 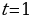 с скорость
с скорость 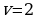 м/с, а путь
м/с, а путь 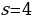 м.
м.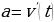 . Затем найти
. Затем найти 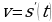 .
.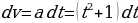 , откуда
, откуда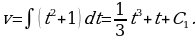
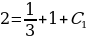 , откуда
, откуда 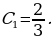
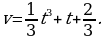
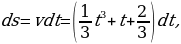 откуда
откуда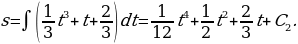
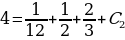 , откуда находим
, откуда находим 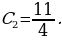
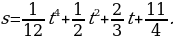
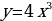 на множестве R.
на множестве R.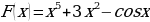 является первообразной функции
является первообразной функции 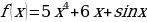 на множестве R.
на множестве R.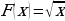 есть первообразная функции
есть первообразная функции 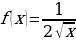 на промежутке
на промежутке 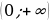 .
.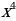 и
и 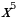 ; б)
; б) 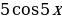 и
и 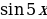 ; в)
; в) 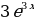 и
и 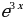 ; г)
; г) 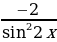 и
и 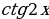 ;
; 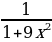 и
и 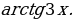 В каких примерах допущены ошибки?
В каких примерах допущены ошибки?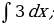
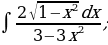
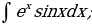
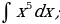
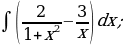
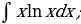
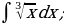
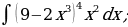
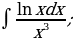
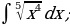
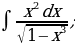
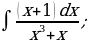
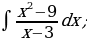
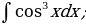
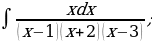
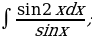
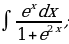
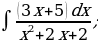
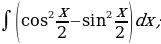
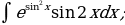
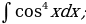
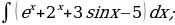
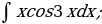
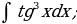
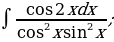
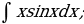
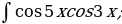
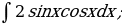
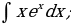
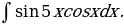
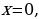 если производная этой функции имеет вид
если производная этой функции имеет вид 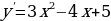 .
.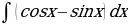 , если при
, если при 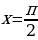 первообразная равна 6.
первообразная равна 6.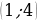 , если угловой коэффициент касательной в каждой точке кривой задается функцией
, если угловой коэффициент касательной в каждой точке кривой задается функцией 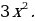
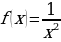 , график которой проходит через точку
, график которой проходит через точку 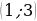 .
.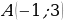 , если угловой коэффициент касательной к кривой в каждой точке кривой равен утроенному квадрату абсциссы точки касания.
, если угловой коэффициент касательной к кривой в каждой точке кривой равен утроенному квадрату абсциссы точки касания.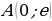 , если угловой коэффициент касательной к кривой в любой ее точке кривой равен
, если угловой коэффициент касательной к кривой в любой ее точке кривой равен 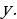
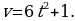 Найти уравнение движения, если за время
Найти уравнение движения, если за время 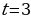 с тело прошло путь
с тело прошло путь 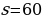 м.
м.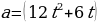 м/с2. Найдите закон движения точки
м/с2. Найдите закон движения точки 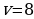 м/с, а путь
м/с, а путь 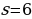 м.
м.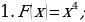 4. Ошибки допущены в примерах а) и д); 5. 1)
4. Ошибки допущены в примерах а) и д); 5. 1) 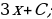 2)
2) 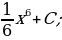 3)
3) 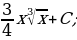 4)
4) 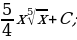 5)
5) 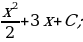 6)
6) 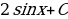 ; 7)
; 7) 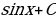 ; 8)
; 8) 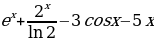 ; 9)
; 9) 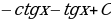 ; 10)
; 10) 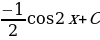 ; 11)
; 11) 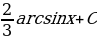 ; 12)
; 12) 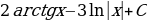 ; 13)
; 13) 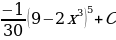 ; 14)
; 14) 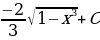 ; 15)
; 15) 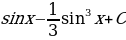 ; 16)
; 16) 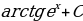 ; 17)
; 17) 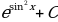 ; 18)
; 18) 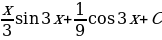 ; 19)
; 19) 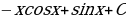 ; 20)
; 20) 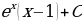 ; 21)
; 21) 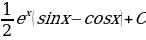 ; 22)
; 22) 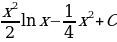 ; 23)
; 23) 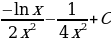 ;24)
;24) 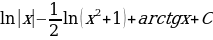 ; 25)
; 25) 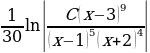 ; 26)
; 26) 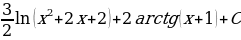 ; 27)
; 27) 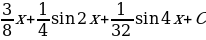 ; 28)
; 28) 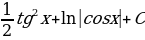 ; 29)
; 29) 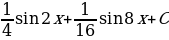 ; 30)
; 30) 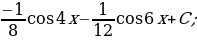 6.
6. 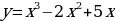 ; 7.
; 7. 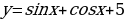 ; 8.
; 8. 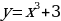 ; 9.
; 9. 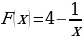 ; 10.
; 10. 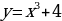 ; 11.
; 11. 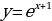 ; 12.
; 12. 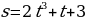 ; 13.
; 13. 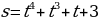 .
.









