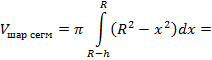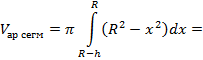| Объем шарового сегмента, шарового слоя и шарового сектора |
| На уроке мы рассмотрим части шара: шаровой сегмент, шаровой слой и шаровой сектор
|
|
| Определение. Шаровым сегментом называется часть шара, отсекаемая от него какой-нибудь плоскостью.
Секущая плоскость разбивает шар на два шаровых сегмента.
Круг, получающийся в сечении, называется основанием каждого из этих сегментов, а длины отрезков диаметра, перпендикулярного к секущей плоскости, называются высотами сегмента. На экране высоты сегментов обозначены 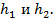
| 
|
| Теорема. Объем шарового сегмента равен 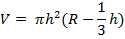
где R – радиус шара; h – высота сегмента.
Доказательство. Применим уже известную нам интегральную формулу для вычисления объемов тел.
Проведем ось Ox перпендикулярно к плоскости основания. Тогда произвольное сечение, проведенное перпендикулярно к оси Ox, будет кругом, а его площадь S выражается формулой:
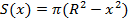 , при R- hxR. , при R- hxR.
Эту формулу мы получили при выводе формулы объема шара. Вычислив соответствующий определенный интеграл, получаем:
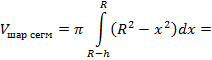
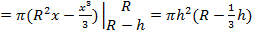 . .
Итак,
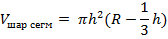
Ч. т. д.
| Теорема. Объем шарового сегмента равен 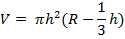
где R – радиус шара; h– высота сегмента.
Доказательство. Проведем ось Ox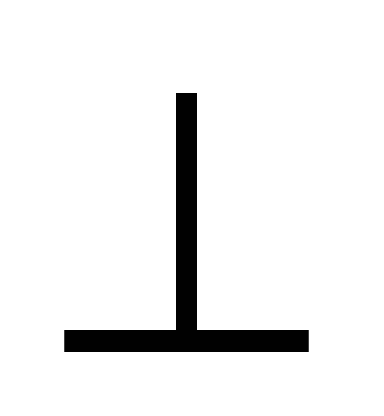 к плоскости основания. к плоскости основания. Тогда произвольное сечение, проведенное 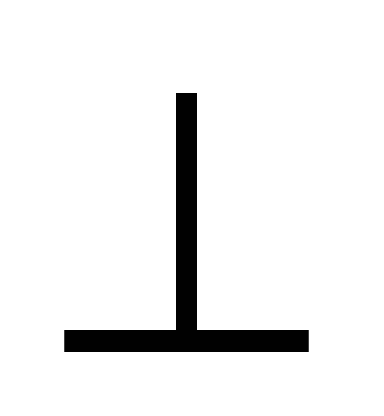 Ox, будет кругом, а его площадь S выражается формулой: Ox, будет кругом, а его площадь S выражается формулой:
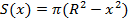 , при R- hxR. , при R- hxR.
Вычислим соответствующий интеграл: 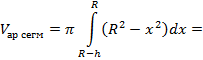
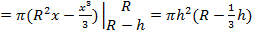 . .
Итак,
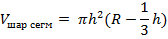
Ч. т. д.
|
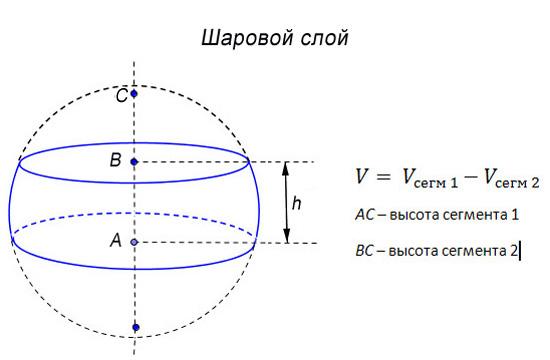
| Определение. Шаровым слоем называется часть шара, заключенная между двумя параллельными сечениями. Расстояние h между сечениями называется высотой слоя, а сами сечения – основаниями слоя.
Объем шарового слоя можно вычислить как разность объемов двух шаровых сегментов.
Например, объем шарового слоя, изображенного на экране, равен разности объемов шаровых сегментов с высотами AC и BC.
| 
|
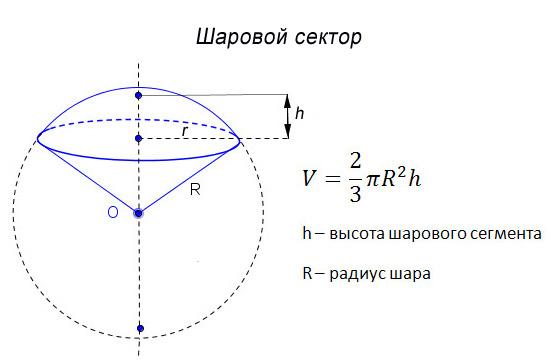
| Определение. Шаровым сектором называется тело, полученное вращением кругового сектора с углом меньшим 900, вокруг прямой, содержащей один из ограничивающих сектор радиусов.
Шаровой сектор состоит из шарового сегмента и конуса.
Если радиус шара равен R, а высота шарового сегмента равна h, то объем V шарового сектора вычисляется по формуле: 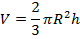
| 
|
| Переходим к решению задач. |
|
| Задача 1 Диаметр шара разделен на три равные части и через точки деления проведены плоскости, перпендикулярные к диаметру. Найдите объем получившегося шарового слоя, если радиус шара равен R.
Дано: Шаровой слой. R – радиус шара D –диаметр, точки C, D делят диаметр на три равные части: AC = CD = DC Нужно найти: 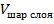
| Задача 1 Диаметр шара разделен на три равные части и через точки деления проведены плоскости, перпендикулярные к диаметру. Найдите объем получившегося шарового слоя, если радиус шара равен R. 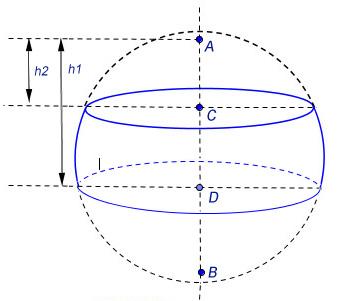
Дано: Шаровой слой R – радиус шара AB–диаметр, 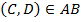 AC = CD = DC Найти :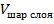
81 |
| Решение: Объем шарового слоя можно найти как разность объемов двух шаровых сегментов, с высотами AD и AC.
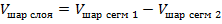
Обозначим высоты сегментов через 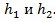 На чертеже отрезок AB – диаметр шара и он равен двум радиусам, высота первого сегмента h1 — отрезок AD, высота второго h2 — отрезок AC.
Так как по условию задачи, точки C и D делят диаметр шара AB на три равные части (AC = СD = DB), то 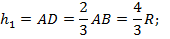
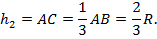
Общая формула для нахождения объема шарового сегмента: 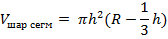
Найдем объем большего сегмента: Найдем объем меньшего сегмента: Теперь мы можем вычислить объем шарового слоя, вычислив их разность:
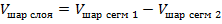
Ответ:
| Решение. 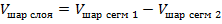
Обозначим высоты сегментов через 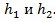
На чертеже AB – диаметр шара, AB = 2R,   . .

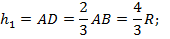
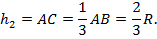
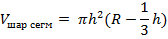

Ответ: |
| Задача 2 Радиус основания шарового сегмента 8 см, а его высота – 4 см. Найти объем сегмента.
Дано: Шаровой сегмент. Радиус основания r=8 см. Высота h = 4 см. Нужно найти объем шарового сегмента V.
| Задача2. Радиус основания шарового сегмента 8 см, а его высота – 4 см. Найти объем сегмента.
Дано: Шаровой сегмент r= 8 см h = 4 см Найти: Vсегм.
|
| Решение. Формула для вычисления объема шарового сегмента: 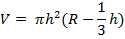
где R – радиус шара; h – высота сегмента.
Найдем радиус шара R.
Проведем ось Ox перпендикулярно основанию шарового сектора. Она пройдет через центр основания (свойство высоты, опущенной из центра шара на секущую плоскость) и будет перпендикулярна его радиусу ( ). ).
Рассмотрим осевое сечение.
Так как OA = OB = R, то OC = R –AC = R – 4
 – прямоугольный ( – прямоугольный ( . .
По теореме Пифагора: 
После подстановки значений получим уравнение с одной переменной: 
Решая это уравнение, найдем R. 
8R= 80; R = 10 Теперь можно вычислить объем Ответ:  | Решение. Формула для вычисления объема шарового сегмента: 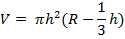
где R – радиус шара; h– высота сегмента.
Найдем радиус шара R. Проведем ось Ox перпендикулярно основанию шарового сектора.
Рассмотрим осевое сечение. Так как OA =OB = R, то OC = R –AC = R – 4  – прямоугольный ( – прямоугольный ( . .
По теореме Пифагора  . .
Подставив значения, получим уравнение: 
Решая его, найдем R. 
8R = 80; R = 10
Вычисляем объем
Ответ:  |
| Задача 3. Найдите объем шарового сектора, если радиус окружности основания соответствующего шарового сегмента равен 60 см, а радиус шара равен 75 см.
Дано: Шаровой сектор. r = 60 см R = 75 см Найти:
Решение. Формула для нахождения объема шарового сектора:  , ,
где R – радиус шара; h – высота шарового сегмента.
Радиус шара нам известен по условию задачи. Не известно значение высоты h.
Для нахождения h проведем ось Ox перпендикулярно основанию шарового сектора и рассмотрим осевое сечение.
На чертеже AO = OB = R, поэтому h = CB = R – CO. Отрезок CO можно найти из треугольника ACO. Так как ось Ox перпендикулярна основанию сегмента, то она перпендикулярна его радиусу ( . . Треугольник AOC – прямоугольный. По теореме Пифагора: = 45см Теперь можно найти h: h = R – CO=75 – 45=30 см Осталось вычислить объем: Ответ: 112 500 πсм3.
| Задача 3. Найдите объем шарового сектора, если радиус окружности основания соответствующего шарового сегмента равен 60 см, а радиус шара равен 75 см.
Дано: шаровой сектор r= 60 см R = 75 см Найти: Решение. Формула для нахождения объема шарового сектора:  , ,
где R – радиус шара; h – высота шарового сегмента. Для нахождения h проведем ось Ox перпендикулярно основанию шарового сектора и рассмотрим осевое сечение. Так как AO = OB = R, то h = CB = R – CO.
ΔACO– прямоугольный ( ): ): =45см Находим h: h = R –CO=75 – 45=30 см Вычисляем объем: Ответ: 112 500 πсм3.
|