Обучение учащихся доказательству теорем в контексте деятельностной концепции уде

ПЕДАГОГИЧЕСКИЕ ИССЛЕДОВАНИЯ

ОБУЧЕНИЕ УЧАЩИХСЯ ДОКАЗАТЕЛЬСТВУ ТЕОРЕМ В КОНТЕКСТЕ ДЕЯТЕЛЬНОСТНОЙ КОНЦЕПЦИИ УДЕ

TEACHING STUDENTS TO PROVE THEOREMS IN THE CONTEXT OF THE ACTIVITY THEORY OF DUE

И. В. Ульянова

В статье раскрываются особенности методики обучения учащихся доказательству планиметри­ческих теорем с использованием блоков укрупнен-

I. V. Ulyanova

The article describes the peculiarities of the methods of teaching students to prove plane geometry theorems using blocks of enlarged problems. It is argued that

85

ных задач. Эти блоки являются основным сред­ством обучения учащихся геометрии в контексте деятельностной концепции укрупнения дидакти­ческих единиц (УДЕ), которая способствует соз­данию единой методологической основы для форми­рования понятий, обучения решению задач и дока­зательству теорем и др.

Ключевые слова: теория и методика обучения ма­тематике, теорема, доказательство теоремы, за­дача, укрупнение дидактических единиц (УДЕ), деятельностная концепция УДЕ, блоки укрупнен­ных задач.

these blocks are the primary means of teaching stu­dents geometry in the context of the activity theory of the didactic unit enlargement (DUE). The given the­ory promotes the development of the integrated meth­odological base to formulate notions, to teach to solve problems, to prove theorems, etc.

Keywords: theory and methods of teaching mathemat­ics, theorem, to prove theorems, problem, didactic unit enlargement (DUE), activity theory of DUE, blocks of enlarged problems.

Современная востребованность информацион­ных технологий во всех сферах общества влечет за собой соответствующую модернизацию систе­мы образования, выражающуюся, в частности, в поиске средств, методов, технологий повышения уровня интел­лектуального развития школьников. Последнее обосно­вывает актуальность многих проблем математического образования, в том числе и проблемы обучения учащих­ся доказательству.

В школьном курсе математики доказательства всег­да являлись источником и условием формирования мыслительных операций учащихся, их логического, аб­страктного, дедуктивного и эвристического мышления, развития у них воображения, навыков исследователь­ской деятельности, самостоятельной активности, по­знавательного интереса и т. д. Доказательства также выступают хорошим способом систематизации учебно­го материала, средством мотивации и получения уча­щимися новых знаний, установления связей между изу­чаемым материалом и уже изученным ранее. Велико и общекультурное значение доказательств. Однако для максимального проявления указанных свойств необхо­дима специально организованная деятельность по обу­чению школьников доказательству, включающая в себя ряд этапов, соответствующих разным возрастным кате­гориям обучаемых. А именно:

• этап формирования у учащихся потребности в ло­гических доказательствах и навыков дедуктивных умоза­ключений, а также понимания ими того факта, что из од­них утверждений логическим путем можно выводить но­вые утверждения (5-6-е классы);

• этап формирования умений выполнять цепочки дедуктивных умозаключений, применять некоторые эв­ристики, преобразовывать требование теоремы в рав­носильное ему или в такое, из которого данное вытекает как следствие, выводить вспомогательные задачи и т. д. (6-7-е классы);

• этап обучения анализу доказательства (выделение отдельных логических шагов, поиск и устранение логиче­ских пробелов, развертывание дедуктивных умозаключе­ний в логическую схему, выделение идеи доказательства и его воспроизведению, применение эвристических при­емов) (7-й класс);

• этап обучения самостоятельному поиску доказа­тельства, выделению его идеи и ее последующей реали­зации (7-8-е классы);

• этап обучения умению опровергать предложен­ные доказательства (9-10-е классы) [1].

Неотъемлемым компонентом обучения учащихся доказательству выступает обучение их доказательству теорем.

Впервые термины «теорема» и «доказательство тео­ремы» вводятся на третьем из указанных выше этапов, что соответствует началу систематического изучения гео­метрии в 7-м классе. В целом процесс изучения теоремы разбивается на следующие этапы:

• мотивация изучения теоремы;

• ознакомление с фактом, отраженным в теореме;

• формулировка теоремы;

• усвоение содержания теоремы;

• ознакомление со способом доказательства теоремы;

• доказательство теоремы;

• применение теоремы;

• установление связи теоремы с другими теоре­мами [1].

При этом, как показывает опыт ведущих учителей, установление связей между отдельными шагами доказа­тельства теоремы, нередко представляющего собой до­статочно длинную цепь последовательно связанных де­дуктивных умозаключений, как и их выделение и обосно­вание, представляет для многих семиклассников (да и для более старших учащихся) значительную трудность. К тому же не следует спешить с привлечением школьников к са­мостоятельному доказательству. Учащиеся должны снача­ла разобраться в структуре готовых доказательств и нау­читься работать с ними. Поэтому традиционно педагоги на этапе ознакомления учащихся со способом доказа­тельства теоремы представляют им именно готовые дока­зательства с последующим их анализом и воспроизведе­нием. Повышению эффективности такой работы значи­тельно способствует использование на этом этапе (как и на других этапах работы с теоремой) различных приемов технологии укрупнения дидактических единиц (УДЕ).

86

Технология УДЕ - это модель совместной педагогиче­ской деятельности, реализующая содержательное обоб­щение, состоящее из интегративных единиц усвоения,

Рис. 1. Граф-схема доказательства

которые включают взаимосвязанные, а иногда взаимои­сключающие части и образуют целостность. В современ­ных условиях возрастания требований к качеству приоб­ретаемых учащимися знаний, умений и навыков при со­храняющейся тенденции к сокращению количества часов, отводимых на изучение дисциплин естественно-матема­тического цикла, увеличивающей ценность каждого учеб­ного часа, данная технология является достаточно акту­альной. Она позволяет повышать качество образования при меньшем потреблении временных ресурсов. Дей­ствительно, к примеру, использование при обучении уча­щихся доказательству теорем такого ее приема, как при­ем освоения и составления граф-схем, позволяет охватить единым взором все доказательство и увидеть те его дета­ли, которые остаются в тени при словесном способе, не­редко представляемом ученику запутанным и сложным. Это позволяет обучаемым быстрее понять применяемый способ доказательства, а также увеличивает степень осо­знанности ими других возможных вариантов доказатель­ства или образования новых теорем на базе исходной. К тому же, по составленной схеме ученикам легче обнару­жить и исправить допущенную ошибку, развивая таким образом у себя элементы самоконтроля. Подобное на­глядно демонстрирует граф-схема (рис. 1) доказательства прямой и обратной теорем о свойствах и признаках па­раллельных прямых, записанных соответственно над чер­той и под ней в следующем предложении:

«Если при пересечении двух ^паР^{аллельных} прямых

секущей

образуются

соответственные

^углы равны ^то

такие

углы равны

прямые параллельны

».

При обучении учащихся доказательству теорем огром­ным потенциалом обладают блоки укрупненных задач - конструкции из нескольких задач, объединенных в единое целое на основе принципа общности деятельности по их решению. Данный принцип подразумевает укрупнение ре­шения какой-либо последующей задачи в блоке посред­ством выполнения действий, дополняющих решение одной жение в сознании ученика анало­гичных, противоположных, взаим­но обратных действий, операций, понятий, теорем и т. п., что способ­ствует наряду с вышесказанным до­стижению целостности математи­ческих знаний как главного условия развития и саморазвития интеллек­та учащихся, их углубления и расширения. Например, че­рез такие блоки можно изучать теоремы, дополняющие материал учебника. Продемонстрируем сказанное, обра­тившись к следующему блоку задач:

1. Четырехугольник A1B1C1D1 вписан в квадрат ABCD так, что АА1 = ВВ1 = СС1 = DD1. Докажите, что ABCD - квадрат.

2. На сторонах квадрата ABCD со стороной а от­мечены точки А1, В1, С1, D1 так, что АА1 = ВВ1 = СС1 = DD1 = b. Вычислите площадь четырехугольника А1В1С1О1.

3. На сторонах квадрата ABCD отмечены точки А1, В1, С1, D1 так, что АА1 = ВВ1 = СС1 = DD1 = а, А1В = В1С = G1D = О1А = b. Вычислите квадрат гипотенузы треугольника ААД

4. Докажите, что в прямоугольном треугольнике АВС с прямым углом С выполняется равенство АВ2 = АС2 + ВС₂.

5. Докажите, что в непрямоугольном треуголь­нике со сторонами а, b, с выполняется неравенство а₂ + b₂ * с₂.

6. Сформулируйте и решите задачу, обратную к задаче 1.4.

Взаимосвязи между решениями задач данного блока отражены на схеме, представленной на рис. 2.

Указанный блок задач 1.1-1.6 эффективно способ­ствует одновременному обучению учащихся доказатель­ству прямой и обратной теорем Пифагора.

Действительно, при последовательном решении за­дач 1.1-1.3 учащиеся фактически знакомятся со способом доказательства прямой теоремы Пифагора, предлагае­мым авторами учебника [2].

одно из направлений методической идеи укрупнения действий, в целом способствую-
	1.1
щей созданию единой методологической осно­вы формирования понятий, обучения реше­нию задач, доказательству теорем и др.	1.3 1.4 1.5 1.6
	1.2	л
В процессе решения блоков укрупненных задач на уроках геометрии происходит сбли-		Рис. 2. Схема взаимосвязей между решениями задач

из предшествующих ей задач. Таким образом реализуется Идея доказательства обратной теоремы Пифагора

Акцентуация внимания учащихся на прямоугольных треугольниках в чертежах к задачам 1.1-1.3 (рис. 3) и их сравнительный анализ с чертежом к задаче 1.4 способ­ствует восприятию последнего (рис. 4) как отдельного фрагмента ранее выполненных чертежей, вызывая подсо­знательное желание достроить его до такого же полного квадрата. Стремление к осуществлению этого желания вызывает идею доказательства прямой теоремы Пифаго­ра, которая как раз и представлена в виде задачи 1.4, и ее последующей реализации.

методом от противного легко возникает и реализуется на основе решения задачи 1.5 данного блока, которая представляет собой противоположную теорему Пифа­гора, являющуюся равносильной обратной теореме. Известно, что если проблематично доказать прямую теорему, то возможно попытаться доказать равносиль­ную ей обратную противоположной теорему. Тогда как в случае проблемности доказательства обратной тео­ремы имеет смысл доказать равносильную ей противо­положную теорему.

С другой стороны, данную задачу 1.5 можно рассма­тривать как полигон для применения только что изученной прямой теоремы, что и предполагает решение задачи 1.6.

Соответствующую работу учащихся с данным блоком задач можно дополнить самостоятельным изучением ими другого способа доказательства обратной теоремы Пифа­гора, отличного от представленного авторами учебни­ка [2] в готовом виде.

в, .г

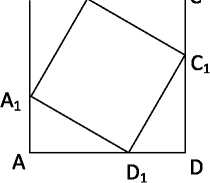
Рис. 3. Чертеж к задачам 1.1-1.3

Рис. 4. Чертеж к задаче 1.4

Таким образом, при обучении учащихся доказатель­ству теорем используемый при этом блок укрупненных задач условно можно разделить на 3 основные части по целевому назначению входящих в них задач:

1. задачи, решения которых способствуют осознанию учащимися способа доказательства теоремы;

2. задачи, решения которых способствуют реализа­ции выявленного способа доказательства;

3. задачи, решения которых способствуют примене­нию данной теоремы и установлению ее связей с ранее изученными теоремами.

Такие части не противоречат указанной выше мето­дике изучения учащимися теорем в целом.

Через такие блоки, как уже было сказано, можно знакомить учащихся не только со способом доказатель­ства теоремы, предлагаемым авторами учебников, но и с другими возможными способами. Подобное демонстри­рует рассмотренный нами блок задач 1.1-1.6, а также блок 2.1-2.3. В последнем решения первых двух задач подсказывают идею доказательства теоремы-признака о равенстве прямоугольных треугольников по гипотенузе и катету иным способом, чем тот, что подразумевает ис­пользование распространенного приема наложения одного треугольника на другой [2]. Этот новый способ предполагает определенное приложение исходных тре­угольников друг к другу и последующее использование свойств равнобедренного треугольника.

1. В равнобедренном треугольнике АВС к основа­нию АС проведена высота ВН. Докажите, что треугольни­ки АВН и СВН равны.

2. (Аналог задачи 2.1). В равнобедренном треуголь­нике АВС к основанию АС проведена медиана ВМ. Дока­жите, что ДАВМ = ДСВМ. Определите вид треугольников АВМ и СВМ.

3. (Теорема-признак). В прямоугольных треугольни­ках АВС и А₁В₁С₁ Z С = Z С1 = 90°, АВ = А1В1, ВС = В1С1. До­кажите, что ДАВС = ДА1В1С1.

В контексте полноценной работы с теоре­мами в предлагаемый учащимся блок укрупнен­ных задач возможно включать и другие задачи, например, мотивирующие изучения теоремы.

Итак, в заключение отметим, что блоки укрупненных задач с одинаковым успехом воз­можно использовать при изучении как плани­метрических, так и стереометрических теорем в отдельности (соответственно 7-9-е и 10­11-е классы), а также для их одновременного и последовательного изучения, соединяя тем са-

мым в сознании учащихся плоскостную и про­странственную геометрии в единое целое. Последнее дает возможность обучаемым проводить более глубо­кие сравнения, широкое обобщение, выдвигать гипоте­зы и предположения, переносить знания, умения и на­выки в новую ситуацию, переосмысливать с новых, бо­лее общих позиций уже изученный ранее материал и т. д. Большую роль при этом будут играть аналогии, интуи­тивные рассуждения, позволяющие приобщить учащих­ся к исследовательской деятельности. Все это в значи­тельной мере способствует повышению интеллектуаль­ного уровня учащихся.

СПИСОК ИСТОЧНИКОВ И ЛИТЕРАТУРЫ

1. Саранцев Г. И. Обучение математическим дока­зательствам в школе: Кн. для учит. - М.: Про­свещение, 2000.

2. Атанасян Л. С. и др. Геометрия: Учеб. для 7-9 кл. сред. шк. - М.: Просвещение, 1991.

NiSH_2010-4.indb 1 01.12.2010 14:27:53