Просмотр содержимого документа
«"Окружность. Взаимное расположение прямой и окружности"»

ТЕМА : ” ОКРУЖНОСТЬ. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ОКРУЖНОСТИ ” .
Окружность.
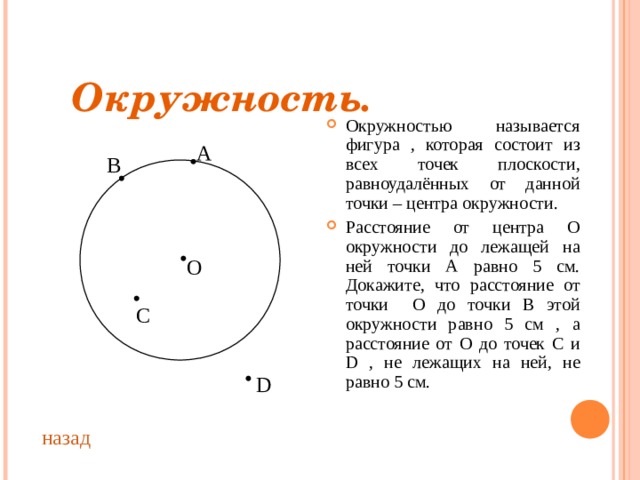
- Окружностью называется фигура , которая состоит из всех точек плоскости, равноудалённых от данной точки – центра окружности.
- Расстояние от центра О окружности до лежащей на ней точки А равно 5 см. Докажите, что расстояние от точки О до точки В этой окружности равно 5 см , а расстояние от О до точек С и D , не лежащих на ней, не равно 5 см.
А
В
О
C
D
назад
2
РАДИУС.
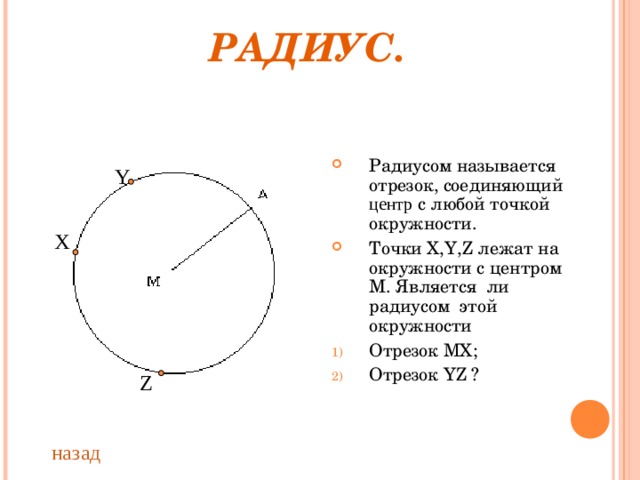
- Радиусом называется отрезок, соединяющий центр с любой точкой окружности.
- Точки X,Y,Z лежат на окружности с центром М. Является ли радиусом этой окружности
Y
X
Z
назад
ХОРДА.
В
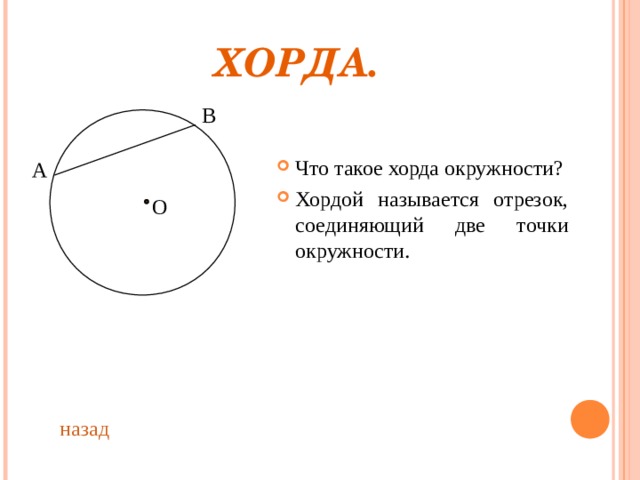
- Что такое хорда окружности?
- Хордой называется отрезок, соединяющий две точки окружности .
А
О
назад
ДИАМЕТР.
А
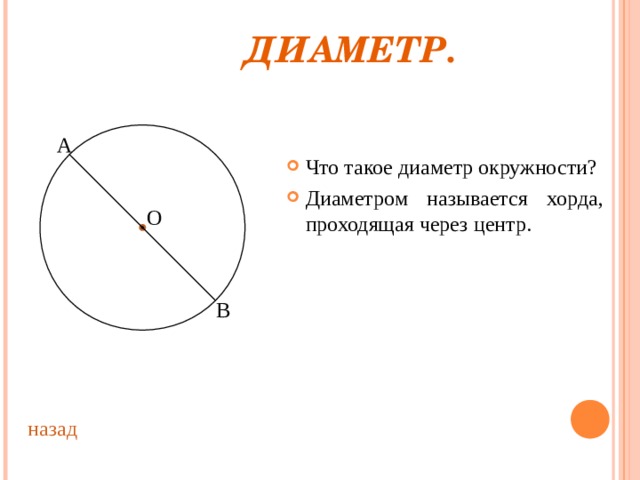
- Что такое диаметр окружности?
- Диаметром называется хорда, проходящая через центр.
О
В
назад
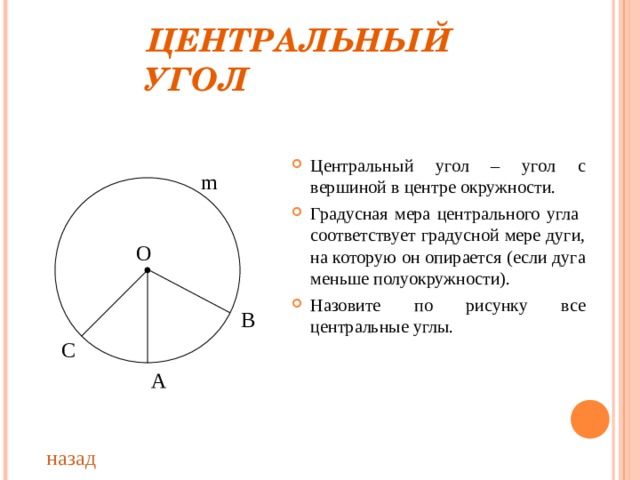
ЦЕНТРАЛЬНЫЙ УГОЛ
- Центральный угол – угол с вершиной в центре окружности.
- Градусная мера центрального угла соответствует градусной мере дуги, на которую он опирается (если дуга меньше полуокружности).
- Назовите по рисунку все центральные углы.
m
О
В
С
А
назад
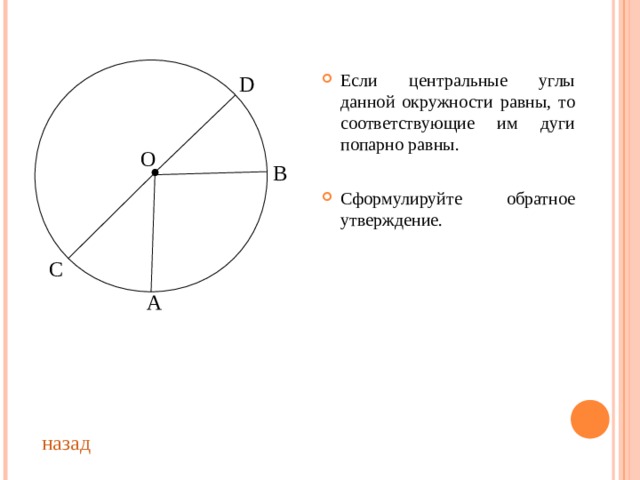
- Если центральные углы данной окружности равны, то соответствующие им дуги попарно равны.
- Сформулируйте обратное утверждение.
D
О
В
С
А
назад
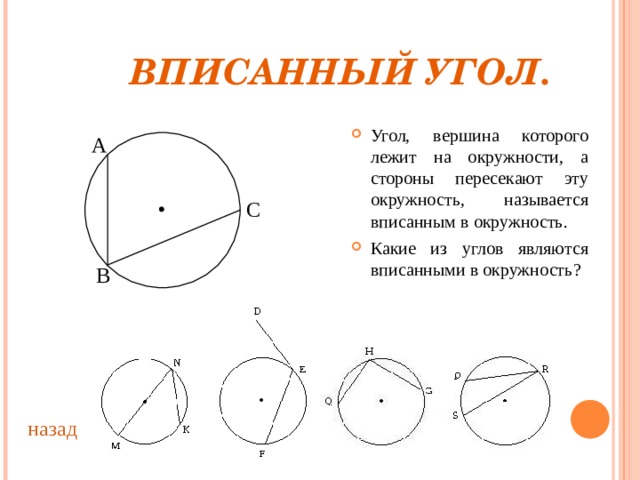
ВПИСАННЫЙ УГОЛ.
- Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным в окружность.
- Какие из углов являются вписанными в окружность ?
А
С
В
назад
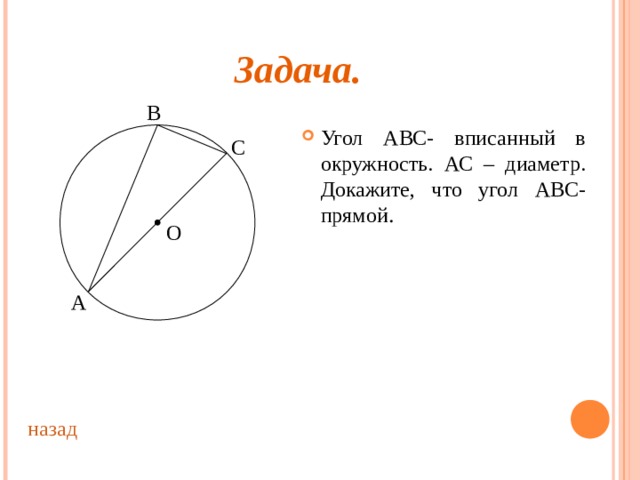
Задача.
В
- Угол ABC- вписанный в окружность. АС – диаметр. Докажите, что угол ABC - прямой .
С
О
А
назад

СВОЙСТВО ВПИСАННОГО УГЛА.
- Докажите, что равны все вписанные в окружность углы, стороны которых проходят через две данные точки окружности, а вершины лежат по одну сторону от прямой, соединяющей эти точки.
назад

ЗАДАЧА.
Точки А, В и С лежат на окружности с центром О, АВС = 50 , АВ : СВ = 5 : 8. Найдите эти дуги и АОС.
назад
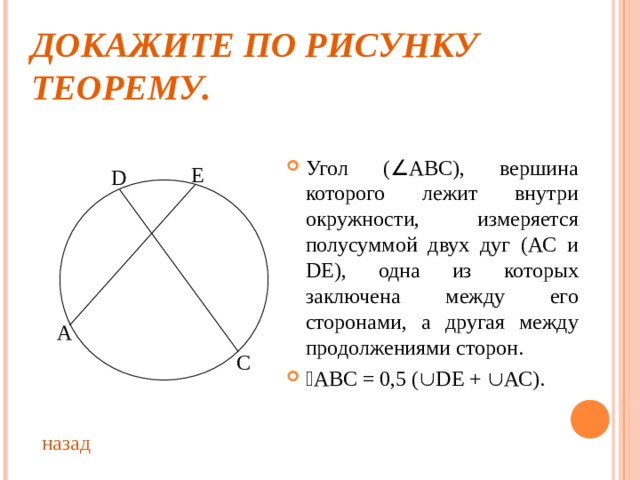
ДОКАЖИТЕ ПО РИСУНКУ ТЕОРЕМУ.
- Угол ( АВС), вершина которого лежит внутри окружности, измеряется полусуммой двух дуг (АС и D Е), одна из которых заключена между его сторонами, а другая между продолжениями сторон.
- АВС = 0,5 ( D Е + АС).
Е
D
А
С
назад

ЗАДАЧА.
Хорды МК и РТ пересекаются в точке А. Найдите длину АМ, если АР = 2 дм, АТ = 24 дм, АМ : КА = 3 : 4.
назад
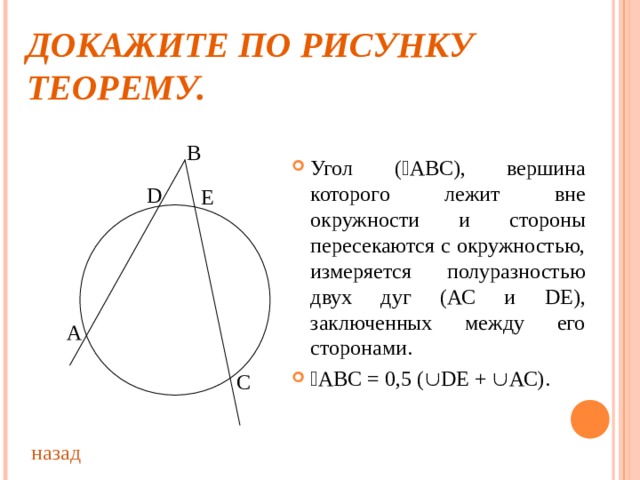
ДОКАЖИТЕ ПО РИСУНКУ ТЕОРЕМУ.
В
- Угол ( АВС), вершина которого лежит вне окружности и стороны пересекаются с окружностью, измеряется полуразностью двух дуг (АС и D Е), заключенных между его сторонами.
- АВС = 0,5 ( D Е + АС).
D
Е
А
С
назад

ЗАДАЧА.
Расстояние от точки А до центра окружности радиуса 5 см равно 10 см. Через точку А проведена секущая, которая пересекает окружность в точках В и С. Найти АС, если точка В делит отрезок АС пополам.
назад
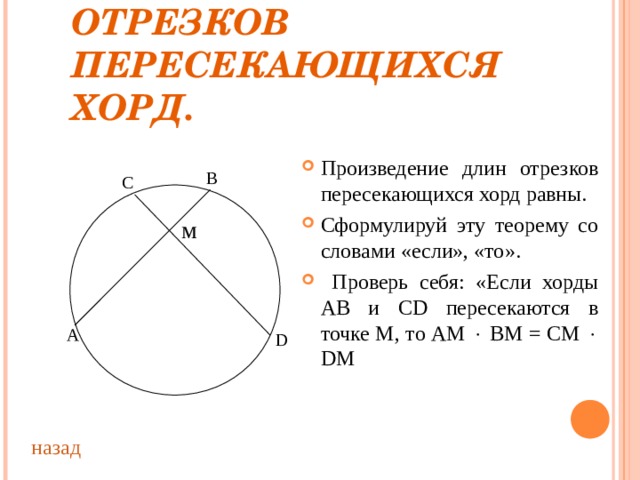
ПРОИЗВЕДЕНИЕ ОТРЕЗКОВ ПЕРЕСЕКАЮЩИХСЯ ХОРД.
- Произведение длин отрезков пересекающихся хорд равны.
- Сформулируй эту теорему со словами «если», «то».
- Проверь себя: «Если хорды АВ и С D пересекаются в точке М, то АМ ВМ = СМ D М
В
С
м
А
D
назад
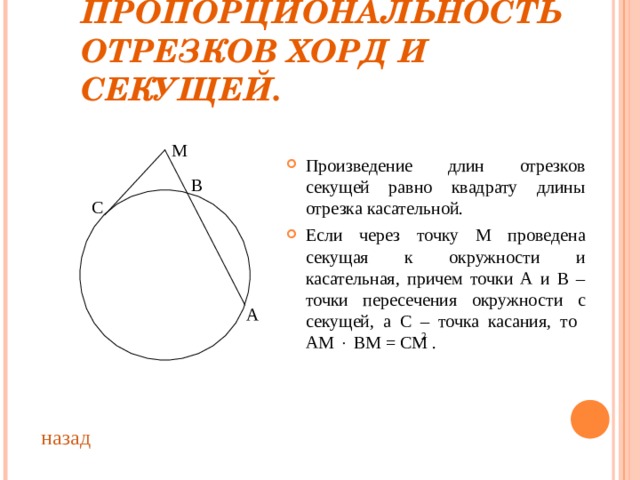
ПРОПОРЦИОНАЛЬНОСТЬ ОТРЕЗКОВ ХОРД И СЕКУЩЕЙ.
М
- Произведение длин отрезков секущей равно квадрату длины отрезка касательной.
- Если через точку М проведена секущая к окружности и касательная, причем точки А и В – точки пересечения окружности с секущей, а С – точка касания, то АМ ВМ = СМ .
В
С
А
назад
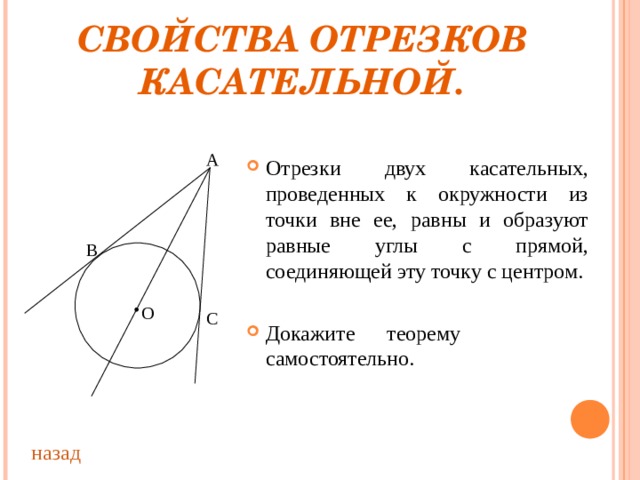
СВОЙСТВА ОТРЕЗКОВ КАСАТЕЛЬНОЙ.
А
- Отрезки двух касательных, проведенных к окружности из точки вне ее, равны и образуют равные углы с прямой, соединяющей эту точку с центром.
- Докажите теорему самостоятельно.
В
О
С
назад

ЗАДАЧА.
Из точки М к окружности с центром О и радиусом 8 см проведены касательные АМ и ВМ (А и В – точки касания). Найти периметр треугольника АВМ, если угол АОВ равен 120 .
назад
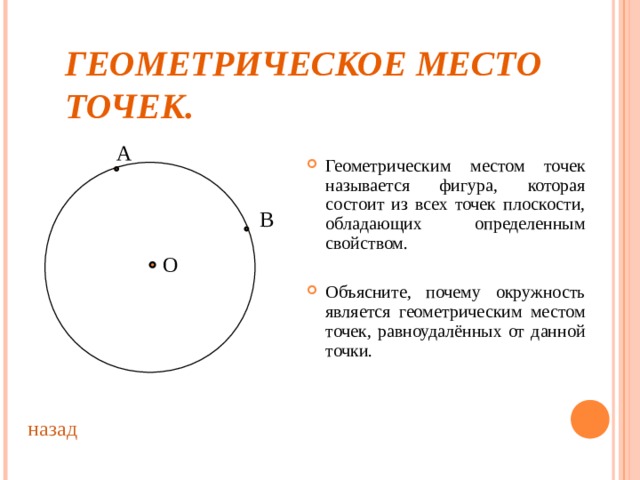
ГЕОМЕТРИЧЕСКОЕ МЕСТО ТОЧЕК.
А
- Геометрическим местом точек называется фигура, которая состоит из всех точек плоскости, обладающих определенным свойством.
- Объясните, почему окружность является геометрическим местом точек, равноудалённых от данной точки.
В
О
назад

ТЕОРЕМА О ГЕОМЕТРИЧЕСКОМ МЕСТЕ ТОЧЕК.
- Геометрическое место точек, равноудалённых от двух данных точек, есть прямая, перпендикулярная к отрезку, соединяющему эти точки и проходящая через его середину.
- Дано: а ; АВ а ; АО = ОВ.
Доказать: а - геометрическое место точек, равноудалённых от А и В.
- Будет ли теорема доказана, если установить, что любая точка прямой а равноудалена от А и В.
М
В
О
А
а
назад
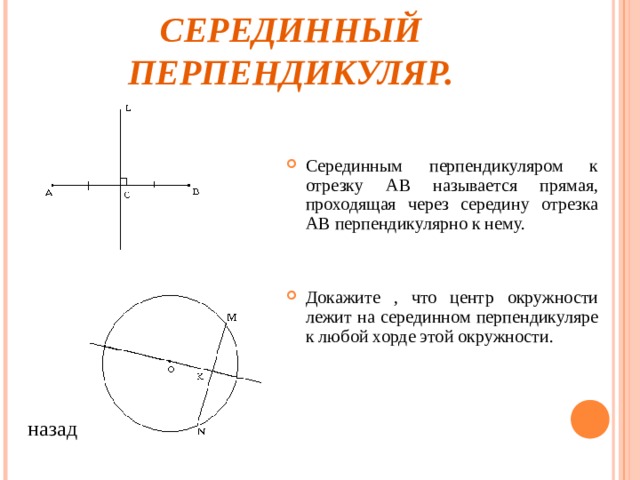
СЕРЕДИННЫЙ ПЕРПЕНДИКУЛЯР.
- Серединным перпендикуляром к отрезку АВ называется прямая, проходящая через середину отрезка АВ перпендикулярно к нему.
- Докажите , что центр окружности лежит на серединном перпендикуляре к любой хорде этой окружности.
назад
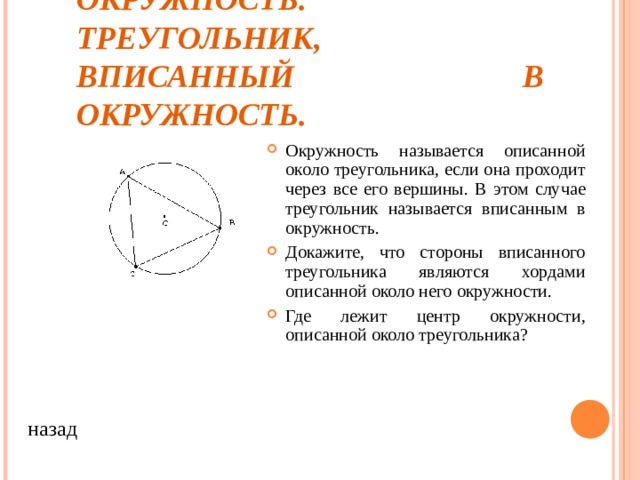
ОПИСАННАЯ ОКРУЖНОСТЬ. ТРЕУГОЛЬНИК, ВПИСАННЫЙ В ОКРУЖНОСТЬ.
- Окружность называется описанной около треугольника, если она проходит через все его вершины. В этом случае треугольник называется вписанным в окружность.
- Докажите, что стороны вписанного треугольника являются хордами описанной около него окружности.
- Где лежит центр окружности, описанной около треугольника?
назад

Задача.
В
- Где лежит центр окружности, описанной около прямоугольного треугольника?
С
О
А
назад

ЗАДАЧА.
Найдите радиус окружности, описанной около треугольника со сторонами 10, 12, и 10 см.
назад

КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ
- Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности Общая точка окружности и касательной называется точкой касания.
- Что можно сказать о сторонах треугольника С D Е по отношению к окружности?
назад
ОКРУЖНОСТЬ, ВПИСАННАЯ В ТРЕУГОЛЬНИК.
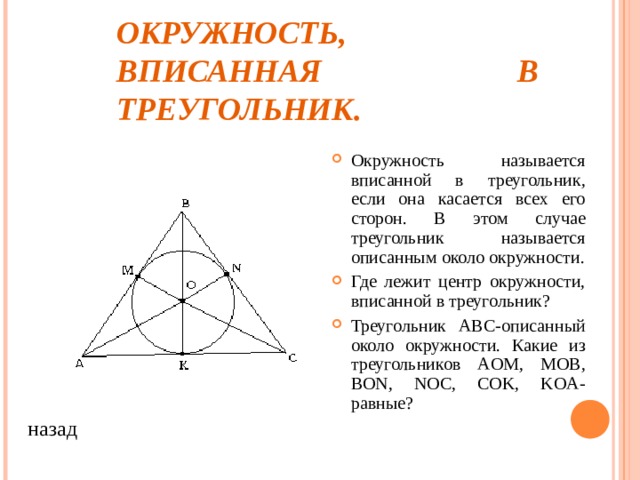
- Окружность называется вписанной в треугольник, если она касается всех его сторон. В этом случае треугольник называется описанным около окружности.
- Где лежит центр окружности, вписанной в треугольник?
- Треугольник ABC- описанный около окружности. Какие из треугольников AOM, MOB, BON, NOC, COK, KOA- равные ?
назад

ЗАДАЧА.
В прямоугольном треугольнике один из углов 30 . Найдите меньшую сторону треугольника, если радиус вписанной окружности равен 4 см.
назад
ОКРУЖНОСТЬ, ОПИСАННАЯ ОКОЛО ЧЕТЫРЕХУГОЛЬНИКА.
В
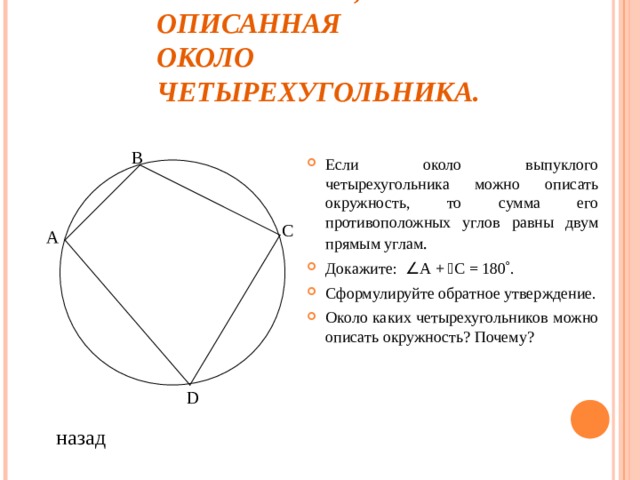
- Если около выпуклого четырехугольника можно описать окружность, то сумма его противоположных углов равны двум прямым углам .
- Докажите: А + С = 180 .
- Сформулируйте обратное утверждение.
- Около каких четырехугольников можно описать окружность? Почему?
С
A
D
назад

ЗАДАЧА.
Диагональ трапеции составляет с большим основанием угол 30 , а центр окружности, описанной возле трапеции, принадлежит этому основанию. Найдите площадь трапеции, если ее боковая сторона равна 2 см.
назад
ОКРУЖНОСТЬ, ВПИСАННАЯ В ЧЕТЫРЕХУГОЛЬНИК
В
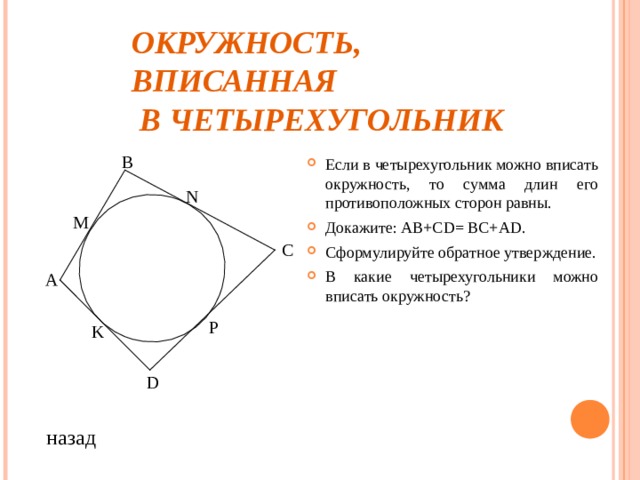
- Если в четырехугольник можно вписать окружность, то сумма длин его противоположных сторон равны.
- Докажите: АВ+С D = ВС+А D .
- Сформулируйте обратное утверждение.
- В какие четырехугольники можно вписать окружность?
N
M
С
А
P
K
D
назад

ЗАДАЧА.
Найдите площадь равнобедренной трапеции, описанной около окружности, если ее основания равны 2 см и 8 см.
назад
















































