Муниципальный этап всероссийской олимпиады школьников по физике
2016-17 учебный год
7 класс
1. Решение
Выразим расстояние: S=6Vвел. Найдем соотношение между скоростями:
S/Vвел +S/Vпеш = 18 мин; Vпеш = Vвел /2; t= 4 S/ Vпеш = 48 мин.
Критерии оценивания:
Выражено расстояние через скорость - 2 б
Выражено соотношение между скоростями - 2б
Выражено соотношение для времени - 2б
Приведён числовой ответ - 2б.
2. Решение
Выполним перевод скоростей : 36 км/ч = 10 м/с; 54 км/ч = 15м/с. Если мысленно превратить три стороны квадрата в прямую линию, то получается что велосипедисты едут навстречу друг другу по прямой линии. В этом случае время до их первой встречи определяется, как расстояние (равное 3 сторонам квадрата) деленное на их суммарную (относительную) скорость
t₁ = 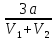 =
=  = 180 с = 3 мин (1)
= 180 с = 3 мин (1)
Для нахождения интервала времени ∆t, необходимого для расчета времени второй встречи сформулируем задачу: эти велосипедисты после первой встречи начинают движение со своими скоростями в противоположным направлениях и до второй встречи проходят четыре стороны квадрата. Следовательно,
∆t =  =
= 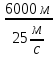 = 240 с = 4 мин (2),
= 240 с = 4 мин (2),
Тогда t₂ = t₁ + ∆t =7 мин (3)
Очевидно, что t₃ отличается от t₂ на тот же самый интервал ∆t, т.к. от момента второй встречи все повторяется, как и после первой, т.е.
t₃ = t₂ + ∆t = 7 мин + 4 мин = 11 мин(4 )
ОТВЕТ: t₁ = 3мин, t₂ = 7 мин, t₃ = 11 мин.
Критерии оценивания:
| 1 | Правильно выполнен перевод единиц измерения скоростей | 1 балл |
| 2 | Получено выражение (1) и вычислено время t1 | 3 балла |
| 3 | Получено выражение (3) и вычислено время t2 | 2 балла |
| 4 | Получено выражение (4) и вычислено время t3 | 2 балла |
3. Решение
Пусть  - масса каждой из частей бруска,
- масса каждой из частей бруска, 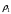 и
и 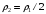 - их плотности. Тогда части бруска имеют объемы
- их плотности. Тогда части бруска имеют объемы  и
и 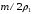 , а весь брусок массу
, а весь брусок массу 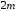 и объем
и объем  . Средняя плотность бруска
. Средняя плотность бруска
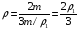 .
.
Отсюда находим плотности частей бруска:
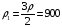 кг/м3,
кг/м3,  кг/м3.
кг/м3.
Критерии оценивания:
1. Определено, что средняя плотность бруска есть 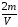 – 1 балл.
– 1 балл.
2. Определены объемы каждой части бруска  и
и 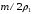 – 2 балла.
– 2 балла.
3. Определен весь объем бруска  – 2 балла.
– 2 балла.
4. Выражена средняя плотность бруска через 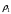 – 1 балла.
– 1 балла.
5. Найдена плотность каждого бруска – по 2 балла.
4. Решение
Расход воды из горячего крана составляет (10 л)/(100 с) = 0,1 л/с, а из холодного крана (3 л)/(24 с) = 0,125 л/с . Следовательно, общий расход воды равен 0,1 л/с + 0,125 л/с = 0,225 л/с . Поэтому кастрюля емкостью 4,5 литра наполнится водой за время (4,5 л)/(0,225 л/с) = 20 с.
ОТВЕТ: кастрюля наполнится водой за 20 с.
Критерии оценивания:
| 1 | Вычислен расход воды из горячего крана | 1 балл |
| 2 | Вычислен расход воды из холодного крана | 2 балла |
| 3 | Вычислен общий расход воды | 2 балла |
| 4 | Вычислено время наполнения кастрюли | 3 балла |
5.

Критерии оценивания:
Рассмотрен ряд из пяти кубиков – 1 балл
Найдена длина ряда кубиков – 2 балла
Найдена длина ребра одного кубика – 2 балла
Найден объём большого куба – 3 балла.
Максимальное количество баллов – 40.
Муниципальный этап всероссийской олимпиады школьников по физике
2016-17 учебный год
8 класс
1. Решение
На систему, состоящую из поплавка и грузила, действуют направленные вниз силы тяжести  (приложена к поплавку) и
(приложена к поплавку) и 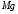 (приложена к грузилу), а также направленные вверх силы Архимеда
(приложена к грузилу), а также направленные вверх силы Архимеда 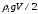 (приложена к поплавку) и
(приложена к поплавку) и  (приложена к грузилу). В равновесии сумма сил, действующих на систему равна нулю:
(приложена к грузилу). В равновесии сумма сил, действующих на систему равна нулю:
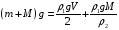 .
.
Отсюда
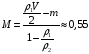 г.
г.
Критерии оценивания:
1. Нарисован рисунок с приложенными к каждому телу силами – 1 балл.
2. Записана сумма сил, действующих на поплавок (с учетом силы натяжения со стороны лески) – 1 балл.
3. Записана сумма сил, действующих на грузило (с учетом силы натяжения со стороны лески) – 1 балл.
4. Исключена сила натяжения и записано условие равновесия системы – 2 балла.
5. Получено конечное выражение для массы грузила – 2 балла.
6. Получено числовое значение – 1 балл.
2. Решение
Выразим высоту налитой жидкости:
h1=m1/ (ρв*S), где S – площадь сечения сосуда. Гидростатическое давление:
p1 = ρв gh1.
Изменение давления Δp= ρв gh2, где
h2= m2/ (ρ2*S), так как Vш = Vв.
Тогда в процентах р1 – 100%
Δp - х %
Получаем ответ на 2,2%
Критерии оценивания:
Уравнение для давления - 2 балла.
Выражена высота налитой жидкости - 2балла.
Выражено выражение для изменения h - 2балла.
Получено соотношение в % - 2балла.
3.

Критерии оценивания:
Найдено время заполнения бассейна одним насосом – 2 балла.
Найдено время заполнения 2/3 бассейна одним насосом – 2 балла.
Найдено время заполнения 1/3 бассейна тремя насосами – 2 балла.
Найдено время заполнения всего бассейна – 2 балла.
4. Решение
Найдем количество теплоты, необходимое для нагревания льда от -20 до 00С. : 840 Дж.
Найдем количество теплоты, необходимое для охлаждения воды от 20 до 00С: -8400 Дж.
Найдем количество теплоты, необходимое для плавления льда: 6640 Дж.
Баланс количества теплоты в сторону нагревания воды: ΔQ=8400-6680-840= =920Дж.
Тогда установится температура: Δt= 920/(0,12*4200) = 1,80С.
Критерии оценивания:
Перевод единиц - 1 балл.
Записана формула количества теплоты для нагревания льда – 1 балл.
Записана формула количества теплоты для плавления льда – 1 балл.
Записана формула количества теплоты для охлаждения воды – 1 балл.
Вычислена разность количества теплоты - 1балл.
Количество теплоты на нагревание общей массы воды – 2 балла.
Приведён числовой ответ -1 балл.
5.

Критерии оценивания:
Введена мощность чайника – 2 балла.
Уравнение теплового баланса в случае со льдом – 2 балла.
Уравнение теплового баланса в случае с водой – 2 балла.
Найдено значение массы чайника – 2 балла.







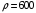 кг/м3. Но на самом деле брусок состоит из двух частей, равных по массе, плотность одной из которых в два раза больше плотности другой. Найдите плотности обеих частей бруска. Массой краски можно пренебречь.
кг/м3. Но на самом деле брусок состоит из двух частей, равных по массе, плотность одной из которых в два раза больше плотности другой. Найдите плотности обеих частей бруска. Массой краски можно пренебречь.
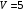 см3 и массу
см3 и массу  г. К поплавку на леске прикреплено свинцовое грузило, и при этом поплавок плавает, погрузившись на половину своего объема. Найдите массу грузила
г. К поплавку на леске прикреплено свинцовое грузило, и при этом поплавок плавает, погрузившись на половину своего объема. Найдите массу грузила 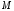 . Плотность воды
. Плотность воды 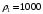 кг/м3, плотность свинца
кг/м3, плотность свинца  кг/м3.
кг/м3.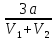 =
=  = 180 с = 3 мин (1)
= 180 с = 3 мин (1) =
= 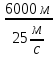 = 240 с = 4 мин (2),
= 240 с = 4 мин (2), - масса каждой из частей бруска,
- масса каждой из частей бруска, 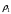 и
и 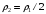 - их плотности. Тогда части бруска имеют объемы
- их плотности. Тогда части бруска имеют объемы  и
и 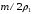 , а весь брусок массу
, а весь брусок массу 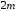 и объем
и объем  . Средняя плотность бруска
. Средняя плотность бруска 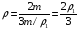 .
.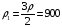 кг/м3,
кг/м3,  кг/м3.
кг/м3.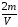 – 1 балл.
– 1 балл.
 (приложена к поплавку) и
(приложена к поплавку) и 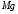 (приложена к грузилу), а также направленные вверх силы Архимеда
(приложена к грузилу), а также направленные вверх силы Архимеда 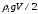 (приложена к поплавку) и
(приложена к поплавку) и  (приложена к грузилу). В равновесии сумма сил, действующих на систему равна нулю:
(приложена к грузилу). В равновесии сумма сил, действующих на систему равна нулю: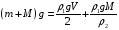 .
.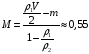 г.
г.











