Операции с множествами. Основные понятия теории графов. Комбинаторика.

7

Раздел 3. Основы дискретной математики, теории вероятностей, математической статистики и их роль в медицине.

Лекция №5

Тема: Операции с множествами. Основные понятия теории графов.

Комбинаторика.

План:

1. Элементы и множества. Операции над множествами и их свойства.

2. Основные понятия теории графов.

3. Основные понятия комбинаторики.

1. Элементы и множества. Операции над множествами и их свойства.

Множество — одно из ключевых понятий математики, в частности, теории множеств и логики.

Понятие множества обычно принимается за одно из исходных (аксиоматических) понятий, то есть не сводимое к другим понятиям, а значит и не имеющее определения. Однако, можно дать описание множества, например в формулировке Георга Кантора: Под «множеством» мы понимаем соединение в некое целое M определённых хорошо различимых предметов m нашего созерцания или нашего мышления (которые будут называться «элементами» множества M).

До XIX века математиками рассматривались в основном конечные множества.

Основы теории конечных и бесконечных множеств были заложены Бернардом Больцано, который сформулировал некоторые из её принципов.

С 1872 г. по 1897 г. (главным образом в 1872—1884 гг.) Георг Кантор опубликовал ряд работ, в которых были систематически изложены основные разделы теории множеств, включая теорию точечных множеств и теорию трансфинитных чисел (кардинальных и порядковых). В этих работах он не только ввёл основные понятия теории множеств, но и обогатил математику рассуждениями нового типа, которые применил для доказательства теорем теории множеств, в частности впервые к бесконечным множествам. Поэтому общепризнано, что теорию множеств создал Георг Кантор.

Множество - это совокупность, набор элементов, объединенных общими свойствами.

Множества обозначаются заглавными латинскими буквами A, B, C… , а элементы множества строчными латинскими буквами a, b, c,…Объекты, из которых состоит множество, называют элементами множества или точками множества. Элементы в множество входят по одному разу, т.е. без повторений.

Множество, которое не содержит ни одного элемента называется пустым и обозначается

Основные числовые множества:

N-{1,2,3,...,n} Множество всех натуральных чисел

Z-{0, ±1, ±2, ±3,...} Множество целых чисел. Множество целых чисел включает в себя множество натуральных.

Q-Множество рациональных чисел.

I - Множество иррациональных чисел

R-Множество всех вещественных чисел( -∞; +∞)

Основные операции:

1. Принадлежность элемента множеству: 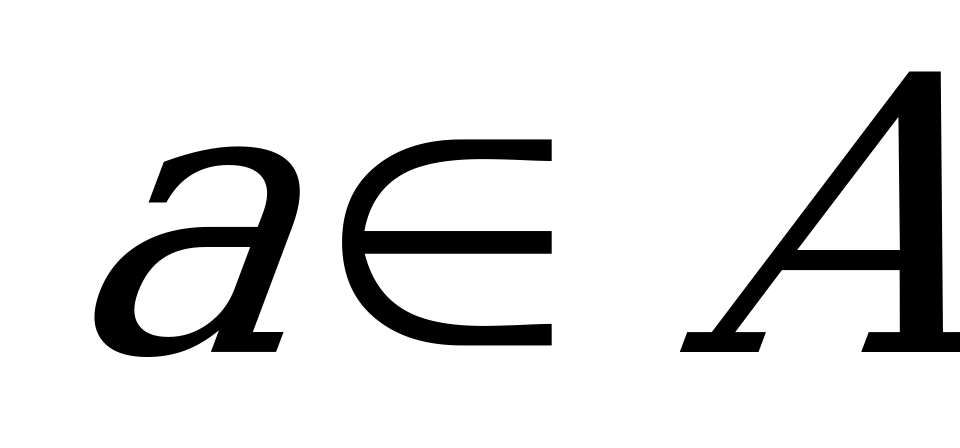; где a- элемент и A- множество (элемент a принадлежит множеству A ).

2. Непринадлежность элемента множеству: где а – элемент и А – множество (элемент a не принадлежит множеству A ).

3. Объединение множеств: А ; Объединением двух множеств А и В называется множество С, которое состоит из элементов множеств А и В, т.е.

или

Пример: {0,1, 3, 5} {1,2,3,4}={0,1,2,3,4,5}

1. Пересечение множеств: А ; Пересечением двух множеств А и В называется множество С которое состоит из общих элементов множеств А и В ,

и

Пример: {0,1, 3, 5} {1,2,3,4}={1,3,5}

1. Разность множеств: .Разностью множеств А и В называется множество A \ B элементы которого принадлежат множеству А, но не принадлежат множеству В.

Пример, если А={1,2,3,4}, B={3,4,5}, то АВ = {1,2}

1. Симметричной разностью множеств А и В называется множество А Δ В, являющееся объединением разностей множеств АВ и ВА, то есть А Δ В = (АВ) (ВА).

Пример, если А={1,2,3,4}, B={3,4,5,6}, то А Δ В = {1,2} {5,6} = {1,2,5,6}

7. Вхождение одного множества в другое множество:

Если любой элемент множества А является элементом множества В , то говорят, что множество А есть подмножество множества В (множество А входит в множество В)

8 . Не вхождение одного множества в другое множество: .

Если существует элемент множества А , который не является элементом множества В, то говорят, что множество А не подмножество множества В (множество А не входит в множествоВ ).

9.Дополнение множества:

Если предположим, что множество А является подмножеством некоторого универсального множества U , тогда определяется операция дополнения:

и

1. Основные понятия теории графов.

Родоначальником теории графов принято считать математика Леонарда Эйлера (1707-1783).

Задача о Кенигсбергских мостах и подобные ей задачи вместе с совокупностью методов их исследования составляют очень важный в практическом отношении раздел математики, называемый теорией графов. Первая работа о графах принадлежала Л. Эйлеру и появилась в 1736 году. Издавна среди жителей Кёнигсберга была распространена такая загадка: как пройти по всем мостам (через реку Преголя), не проходя ни по одному из них дважды? Многие кёнигсбержцы пытались решить эту задачу как теоретически, так и практически, во время прогулок. Но никому это не удавалось, однако не удавалось и доказать, что это даже теоретически невозможно.

В 1736 году задача о семи мостах заинтересовала выдающегося математика, члена Петербургской академии наук Леонарда Эйлера, о чём он написал в письме итальянскому математику и инженеру Мариони от 13 марта 1736 года. В этом письме Эйлер пишет о том, что он смог найти правило, пользуясь которым легко определить, можно ли пройти по всем мостам, не проходя дважды ни по одному из них (в случае семи мостов Кёнигсберга это невозможно).

На упрощённой схеме части города (графе) мостам соответствуют линии (дуги графа), а частям города — точки соединения линий (вершины графа). В ходе рассуждений Эйлер пришёл к следующим выводам:

Число нечётных вершин (вершин, к которым ведёт нечётное число рёбер) графа должно быть чётно. Не может существовать граф, который имел бы нечётное число нечётных вершин.

Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине.

Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком.

Граф кёнигсбергских мостов имел четыре нечётные вершины (то есть все), следовательно, невозможно пройти по всем мостам, не проходя ни по одному из них дважды.

В дальнейшем над графами работали Кениг (1774-1833), Гамильтон (1805-1865), из современных математиков - К. Берж, О. Оре, А. Зыков. С помощью графов часто упрощалось решение задач, сформулированных в различных областях знаний: в автоматике, электронике, физике, химии и др. С помощью графов изображаются схемы дорог, газопроводов, тепло и электросети. Помогают графы в решении математических и экономических задач. Графы формально описывают множество близких ситуаций. Самым привычным примером служит карта автодорог, на которой изображены перекрестки и связывающие их дороги. Перекрестки являются вершинами графа, а дороги - его ребрами.

Познакомимся с основными понятиями теории графов. Граф это множество точек или вершин и множество линий или ребер, соединяющих между собой все или часть этих точек. Вершины, прилегающие к одному и тому же ребру, называются смежными.

Если ребра ориентированны, что обычно показывают стрелками, то они называются дугами, и граф с такими ребрами называется ориентированным графом.

Если ребра не имеют ориентации, граф называется неориентированным.

Графы обычно изображаются в виде геометрических фигур, так что вершины графа изображаются точками, а ребра - линиями, соединяющими точки.

Таким образом, ребро определяется парой вершин. Два ребра, у которых есть общая вершина, также называются смежными (или соседними).

Геометрически граф часто изображают точками плоскости, причем соседние вершины соединены дугами (для орграфа некоторые дуги имеют направление, что обычно отмечают стрелкой).

Помимо этого, в теории графов рассматриваются также мультиграфы – это такие графы, в которых могут быть петли (т. е. некоторая вершина соединена сама с собой ребром) или некоторые пары вершины могут быть соединены между собой несколькими ребрами.

Маршрут в графе – это последовательность соседних (смежных) вершин. Ясно, что можно определить маршрут и как последовательность смежных ребер (в этом случае ребра приобретают направление). Заметим, что в маршруте могут повторяться вершины, но не ребра. Маршрут называется циклом, если в нем первая вершина совпадает с последней.

Путь в графе (иногда говорят простой путь) – это маршрут без повторения вершин (а значит, и ребер).

Контур – это цикл без повторения вершин, за исключением первой вершины, совпадающей с последней.

Последовательности вершин (рис. 1): 1–2–3–4–2–5 не простой путь, а маршрут; последовательности 1–2–3–4–7–5 и 1–2–5 – простые пути; 1–2–3–4–2–5–6–1 –это цикл (но не контур); 1–2–5–6–1 – это контур.

Петля это дуга, начальная и конечная вершина которой совпадают.

Простой граф, граф без кратных ребер и петель.

Степень вершины это удвоенное количество петель, находящихся у этой вершины плюс количество остальных прилегающих к ней ребер.

Пустым называется граф без ребер. Полным называется граф, в котором каждые две вершины смежные.

Граф называется деревом, если он связан и не имеет циклов.

Свойства деревьев

1. Любая пара вершин соединена единственным маршрутом.

2. Количество ребер меньше на одну чем вершин.

3. Удаление хотя бы одного ребра не нарушает его структуру.

4. Если в дерево добавить хотя бы одно ребро то появиться цикл.

3.Основные понятий комбинаторики.

Комбинато́рика (Комбинаторный анализ) — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них (например, частичного порядка). Комбинаторика связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей, и имеет широкий спектр применения в различных областях знаний (например в генетике, информатике, статистической физике).

Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».

Иногда под комбинаторикой понимают более обширный раздел дискретной математики, включающий, в частности, теорию графов.

Основными понятиями комбинаторики являются: размещение, сочетание и перестановка.

Определение 1. Размещением из n элементов по m называется любой упорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.

Число размещений обозначается A и вычисляется по формуле:

Замечание: n!=1*2*3*...*n (читается: "эн факториал"), кроме того полагают, что 0!=1.

Пример 4. Различными размещениями из трех элементов {1, 2, 3} по два будут наборы (1, 2), (2, 1), (1, 3), (3, 1), (2, 3),(3, 2). Размещения могут отличаться друг от друга как элементами, так и их порядком.

Пример 5. Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различные и нечетные?

Решение: т.к. нечетных цифр пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на две разные позиции двух из пяти различных цифр, т.е. указанных чисел будет:

Определение 2. Сочетанием из n элементов по m называется любой неупорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.

Число сочетаний обозначается C и вычисляется по формуле:

Пример 7. Сколькими способами читатель может выбрать две книжки из шести имеющихся?

Решение: Число способов равно числу сочетаний из шести книжек по две, т.е. равно:

Определение 3. Перестановкой из n элементов называется любой упорядоченный набор этих элементов.

Число различных перестановок из n элементов обозначается Pn и вычисляется по формуле Pn=n!.

Пример 8. Сколькими способами семь книг разных авторов можно расставить на полке в один ряд?

Решение: эта задача о числе перестановок семи разных книг. Имеется P7=7!=1*2*3*4*5*6*7=5040 способов осуществить расстановку книг.