Опорный конспект "Аксиомы стереометрии"

Аксиома 1

Аксиома 2

Аксиома 3

Аксиома 4

Если две точки прямой принадлежат плоскости, то и вся прямая лежит в этой плоскости

Если две плоскости имеют хотя бы одну общую точку, то они пересекаются по прямой, проходящей через эту точку.

Через любые три точки, не лежащие на одной прямой можно провести плоскость, и притом только одну.

В пространстве существуют плоскости.

В любой плоскости выполняются все аксиомы, а значит, и все теоремы планиметрии.

Следствие 1

Следствие 2

Следствие 3

Через две пересекающиеся прямые можно провести плоскость и притом только одну

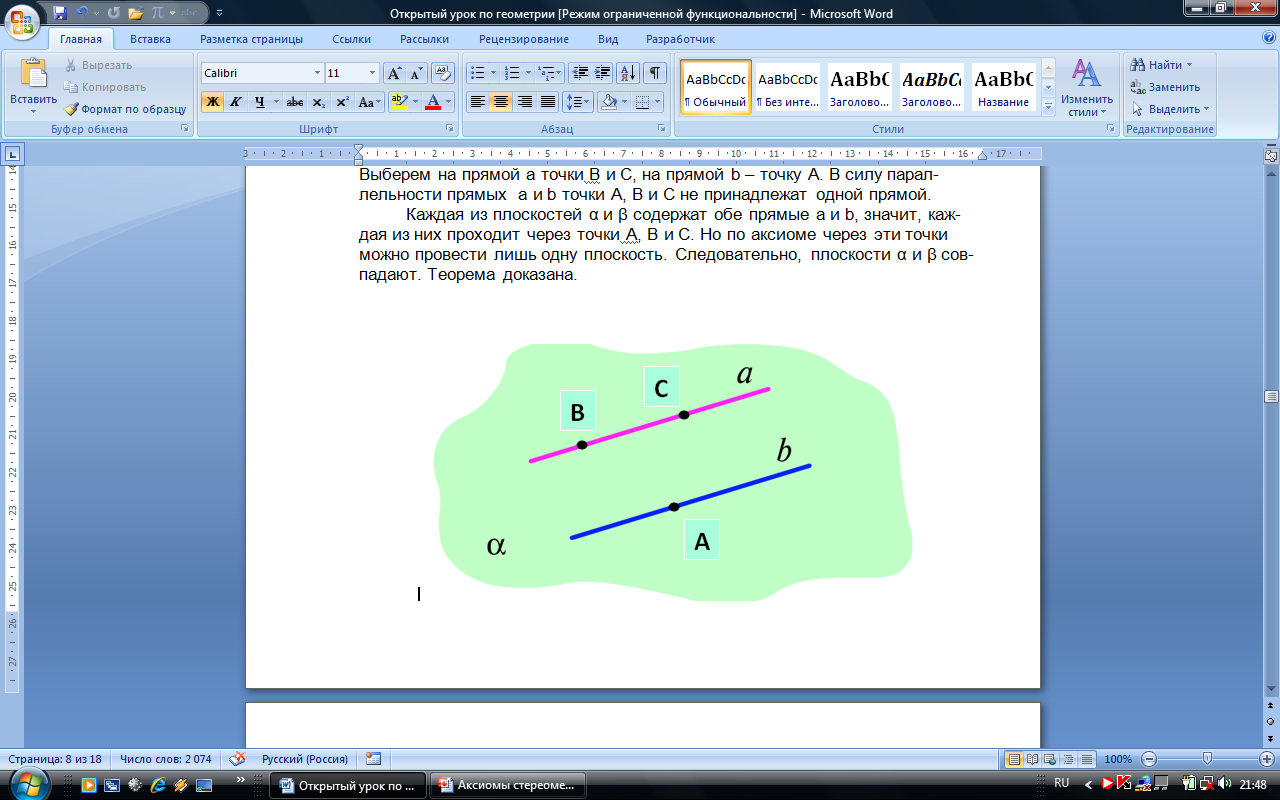
Через две параллельные прямые можно провести плоскость и притом только одну

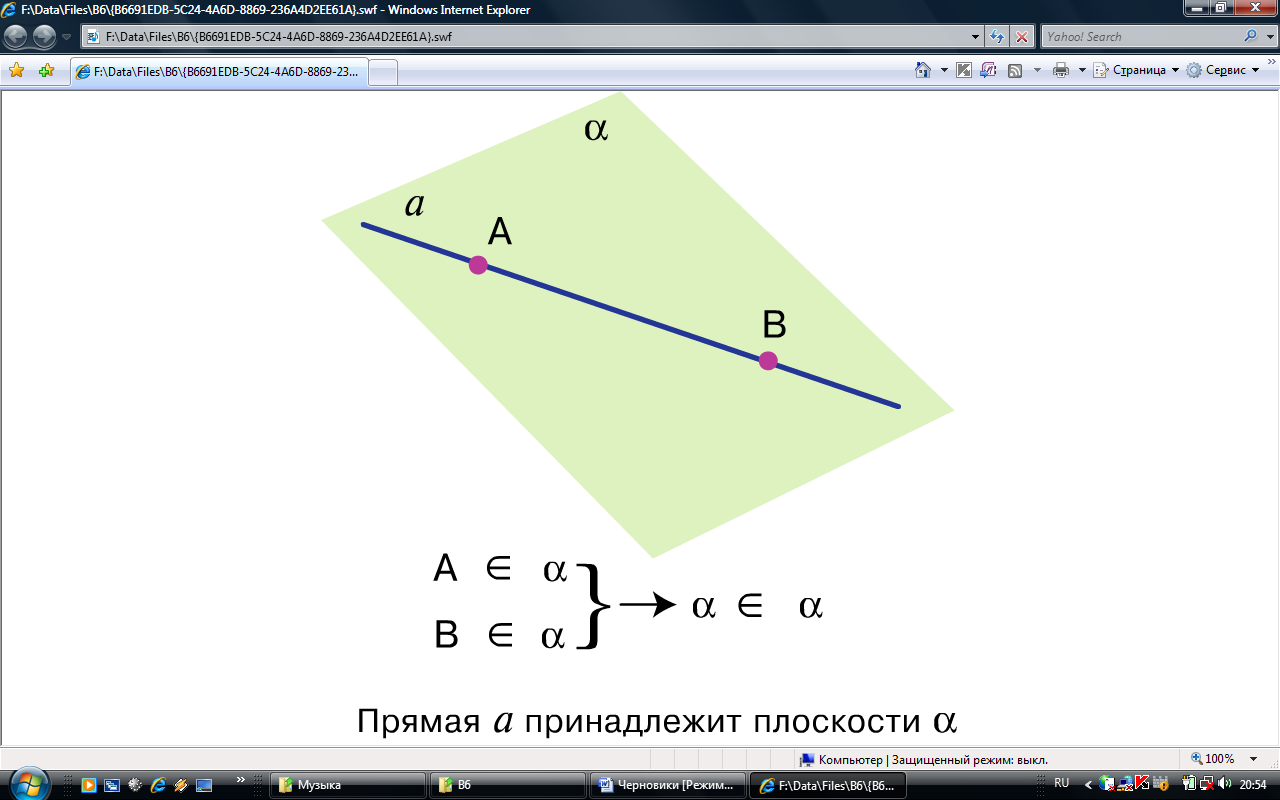
Через любую прямую и не принадлежащую ей точку можно провести плоскость, и притом только одну

Доказательство.

Пусть прямые а и b пересекаются в некоторой точке С. Выберем на прямых а и b любые точки А и В, отличные от С: А ͼ а, В ͼ b. Тогда три точки не принадлежат одной прямой и по аксиоме через них можно провести только одну прямую. Обозначим ее π.

Точки А и С прямой а принадлежат плоскости π, значит плоскость π проходит через прямую а (по аксиоме). Плоскость π проходит через прямую b, так как точки В и С этой прямой принадлежат плоскости π.

Таким образом, плоскость π проходит через прямые а и b, и следовательно, является искомой.

Доказательство Пусть а и b – данные параллельные прямые. Через прямые а и b можно провести плоскость. Обозначим ее α.

Допустим противное. Пусть существует другая плоскость, отличная от α, которая содержит каждую из прямых а и b. Обозначим эту плоскость β. Выберем на прямой а точки В и С, на прямой b – точку А. В силу параллельности прямых а и b точки А, В и С не принадлежат одной прямой.

Каждая из плоскостей α и β содержат обе прямые а и b, значит, каждая из них проходит через точки А, В и С. Но по аксиоме через эти точки можно провести лишь одну плоскость. Следовательно, плоскости α и β совпадают.

Доказательство.

Пусть даны прямая а и не принадлежащая ее точка М.

Выберем на прямой а любые точки В и С. Через точки В и С проходит только одна прямая – прямая а. Так как точка М по условию теоремы не принадлежит прямой а, то точки М, В и С не принадлежат одной прямой.

По аксиоме через точки М, В и С проходит только одна плоскость – плоскость МВС, которую обозначим α. Таким образом, плоскость α проходит через прямую а и точку М и является искомой.

Аксиома 1

Аксиома 2

Аксиома 3

Аксиома 4

Следствие 1

Следствие 2

Следствие 3