МНОГОГРАННИКИ. ПРАВИЛЬНЫЕ МНОГОГРАННИКИ.
Определение. Многогранник- это тело, поверхность которого состоит из конечного числа плоских многоугольников.
Определение. Многогранник называется правильным, если все его грани - равные правильные многоугольники, а все многогранные углы имеют одинаковое число граней. Все ребра правильного многогранника - равные отрезки, все плоские углы правильного многогранника также равны.
Определение. Многогранник называется выпуклым, если он весь лежит по одну сторону от плоскости любой его грани.
Определение. Отрезок, соединяющий две вершины многогранника, не принадлежащие одной грани, называется диагональю многогранника.
Определение. Выпуклый многогранник называется правильным, если:
1) все его грани – равные правильные многоугольники;
2) в каждой вершине сходится одинаковое количество граней;
3) все его двугранные углы равны.
Следствия. В правильном многограннике равны:
а) все ребра;
б) все плоские и многогранные углы и в каждой вершине сходится одинаковое количество ребер.
Существует всего пять правильных многогранников:
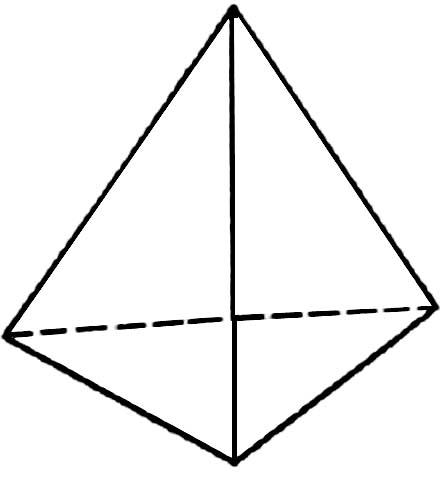
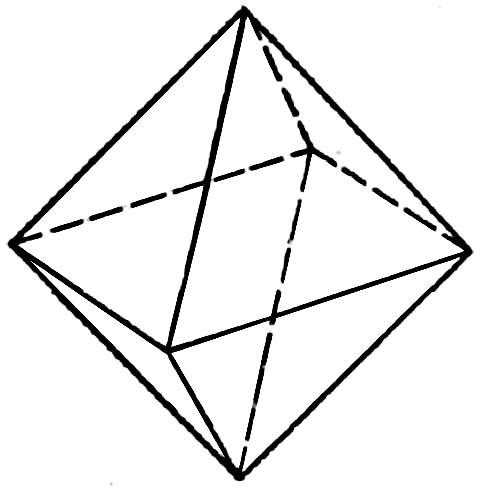
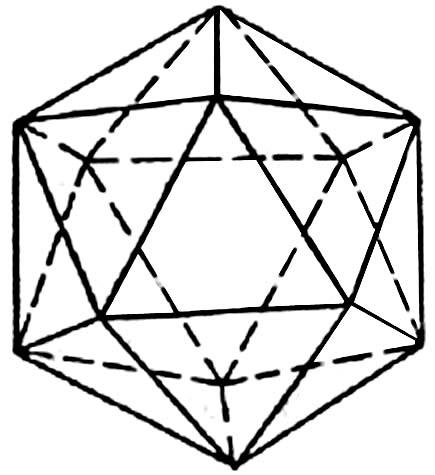
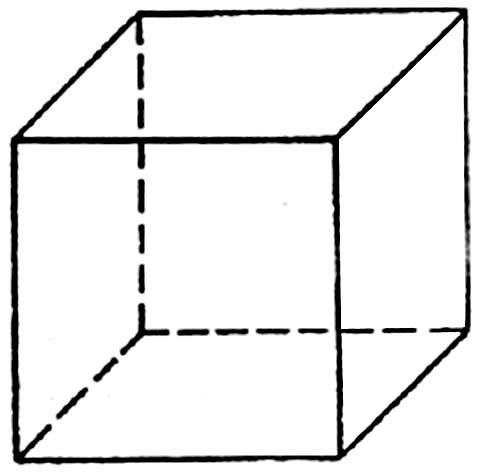
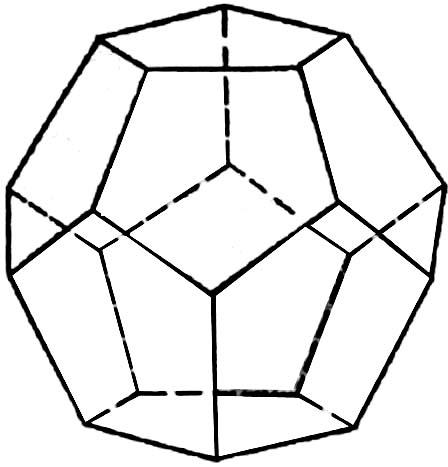
| Правильный тетраэдр | Правильный октаэдр | Правильный икосаэдр | Куб (гексаэдр) | Правильный додекаэдр |
| 
| 
| 
| 
| 
|
| Составлен из четырёх равносторонних треугольников | Составлен из восьми равносторонних треугольников. | Составлен из двадцати равносторонних треугольников | Составлен из шести квадратов | Составлен из двенадцати правильных пятиугольников |
Следствие. Выпуклых многогранников, у которых в каждой грани больше пяти ребер или в каждой вершине сходится более пяти ребер не существует.
Теорема Эйлера: Сумма числа граней и вершин любого многогранника равна числу рёбер, увеличенному на 2. Г + В = Р + 2
Число граней плюс число вершин минус число рёбер в любом многограннике равно 2. Г + В - Р = 2
| Правильный многогранник | Число |
| граней | вершин | рёбер |
| Тетраэдр | 4 | 4 | 6 |
| Куб | 6 | 8 | 12 |
| Октаэдр | 8 | 6 | 12 |
| Додекаэдр | 12 | 20 | 30 |
| Икосаэдр | 20 | 12 | 30 |
П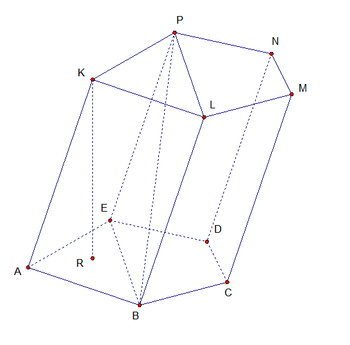 РИЗМА
РИЗМА
Определение. Призмой называется многогранник, который состоит из двух плоских многоугольников, лежащих в разных плоскостях и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки многоугольников.
Основания ABCDE, KLMNP
Боковые грани Все грани, кроме оснований. ABLK, BCML, CDNM, DEPN, EAKP
Боковые ребра AK, BL, CM, DN, EP
Высота KR
Диагональ BP
Диагональное сечение EBLP
Определение. Призма называется прямой, если ее боковые ребра перпендикулярны основаниям. В противном случае призма называется наклонной.
О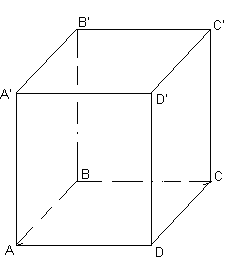 пределение. Прямая призма называется правильной, если ее основания являются правильными многоугольниками.
пределение. Прямая призма называется правильной, если ее основания являются правильными многоугольниками.
Основания правильной призмы являются правильными многоугольниками.
Боковые грани правильной призмы являются равными прямоугольниками.
Боковые ребра правильной призмы равны.
Правильная призма является прямой.
Параллелепипед

ПРЯМОЙ НАКЛОННЫЙ
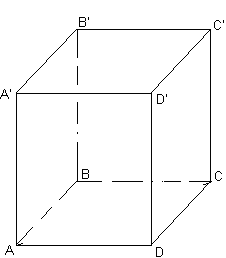
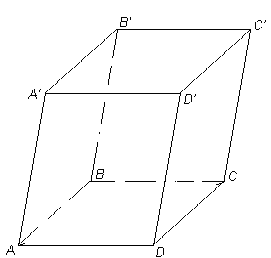
Определение. Если основание призмы есть параллелограмм, то она называется параллелепипедом. У параллелепипеда все грани - параллелограммы.
Грани параллелепипеда, не имеющие общих вершин, называются противоположными.

Теорема 1. У параллелепипеда противолежащие грани параллельны и равны.
AA`BB`=DD`CC`, AA`BB`|| DD`CC`
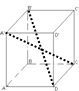
Теорема 2. Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.
A`O = OC, B`O = OD
Определение. Прямой параллелепипед, у которого основанием является прямоугольник, называется прямоугольным параллелепипедом. У прямоугольного параллелепипеда все грани- прямоугольники.
Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
Длина непараллельных ребер прямоугольного параллелепипеда называются его линейными размерами или измерениями. У прямоугольного параллелепипеда их три: длина, ширина, высота.
Центр симметрии прямоугольного параллелепипеда - точка пересечения его диагоналей.
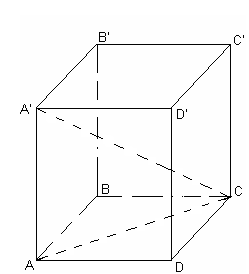
Теорема 3. В прямоугольном параллелепипеде квадрат диагонали равен сумме квадратов трех его измерений.
А`С2= А`А2 + АД2 +ДС2.
Решение задач на тему «Призма. Параллелепипед.»
Задача № 1. Основанием прямой четырехугольной призмы является ромб с диагоналями 1,6 дм и 3 дм, боковое ребро призмы равно 10 дм. Найдите площадь боковой и полной поверхности призмы.
Решение:
И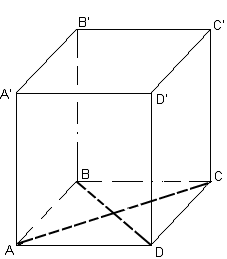 спользуя свойство – диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам, найдем сторону .
спользуя свойство – диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам, найдем сторону .
OD=0,8 дм, OC=1,5 дм
Рассмотрим ∆СОD- прямоугольный.
CD=�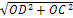 �
�
CD=�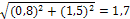 � дм
� дм
AB=BC=CD=AD=1,7 дм
S=4∙ (1,7∙10)=68 дм2.
Ответ: 68 дм2
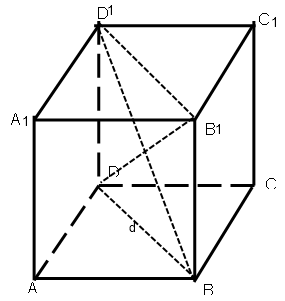
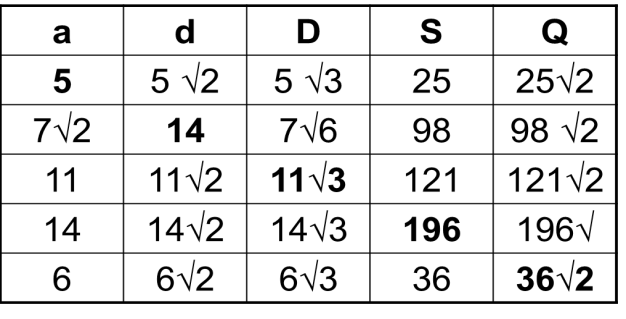
Задача № 2. Ребро куба равно а. заполните таблицу, используя формулы:
Диагональ грани:d= a√2
Диагональ куба: D= a√3
Периметр основания: P= 4a
Площадь грани: S=a2
П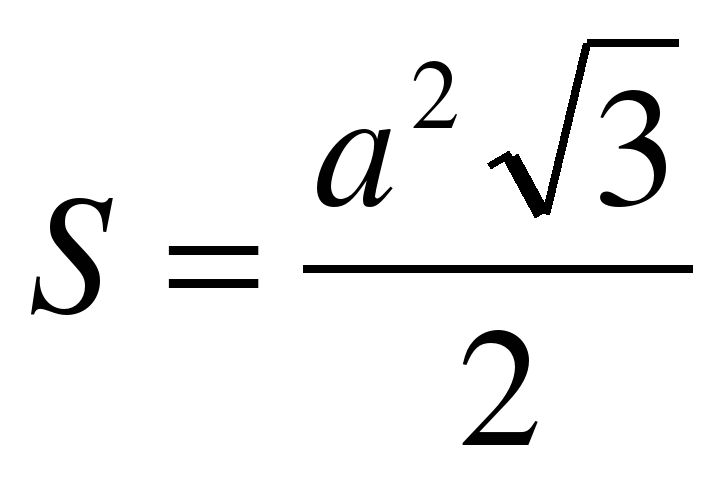 лощадь диагонального сечения: Q= a2√2
лощадь диагонального сечения: Q= a2√2
Площадь поверхности куба: S= 6a2
Периметр и площадь сечения, проходящего через концы трех ребер, выходящих из одной вершины: P= 3a√2 ,
Задача № 3. Сторона основания правильной треугольной призмы равна 8 см, боковое ребро - 6 см. Найдите Sсеч, проходящего через сторону верхнего основания и противолежащую вершину нижнего основания.

Решение:
Треугольник A1B 1C1 - равнобедренный(A1 B=C1B как диагональ равных граней)
1)Рассмотрим треугольник BCC1– прямоугольный
BC1 2 =BС2 +CC1 2
BC1= �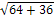 �=10 см
�=10 см
2) Рассмотрим треугольник BMC1– прямоугольный
BC1 2 = BM2 + M C1 2
BM2 = BC1 2 -M C1 2
BM2 =100-16=84
BM= �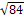 �=2�
�=2�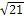 � см
� см
3) Sсеч = � � A1C1 *BM= �
� A1C1 *BM= � �∙8∙2�
�∙8∙2�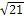 �=8�
�=8�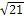 � см2
� см2
Ответ: 8�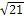 � см2
� см2
ПИРАМИДА
Определение. Пирамидой называется многогранник, который состоит из плоского многоугольника- основания пирамиды, точки, не лежащей в плоскости основания,- вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания.
А- вершина пирамиды;
AB, AC, AD, AE- ребра пирамиды;
ADE, AEB, ABC, ACD- боковые грани пирамиды;
BCDE- основание пирамиды;
AО- высота;
AF- апофема;
AEC-диагональное сечение.
Определение. Пирамида называется правильной, если ее основанием является правильный многоугольник, а основание высоты совпадает с центром этого многоугольника. Осью правильной пирамиды называется прямая, содержащая ее высоту.
У правильной пирамиды боковые ребра равны, а боковые грани – равные равнобедренные треугольники.
Определение. Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.
Если сечение пирамиды параллельно основанию, то мы получим усеченную пирамиду.
Определение. Усеченной пирамидой называется часть пирамиды, заключенная между ее основанием и секущей плоскостью, параллельной основанию.
А1А2 А3А4А5 и В1В2В3В4В5 - нижнее и верхнее основания усечённой пирамиды
А1В1, А2В2, А3В3… - боковые ребра усечённой пирамиды
А1В1 В2А2, В2А2В3А3… - боковые грани усечённой пирамиды.
СН – перпендикуляр, проведённый из какой-нибудь точки верхнего основания к нижнему основанию – называется высотой усечённой пирамиды
Свойства усеченной пирамиды:
Основания усеченной пирамиды — подобные многоугольники.
Боковые грани усеченной пирамиды — трапеции.
Боковые ребра правильной усеченной пирамиды равны и одинаково наклонены к основанию пирамиды.
Боковые грани правильной усеченной пирамиды — равные между собой равнобедренные трапеции и одинаково наклонены к основанию пирамиды.
Двугранные углы при боковых ребрах правильной усеченной пирамиды равны.
Усеченную пирамиду полученную из правильно пирамиды называют правильной.
Высоту боковой грани правильной усеченной пирамиды называют ее апофемой.
У правильной усеченной пирамиды:
Решение задач на тему «Пирамида. Усеченная пирамида».
Задача № 1. Основание пирамиды- параллелограмм со сторонами 6 см и 8 см, высота пирамиды- 12 см, а все боковые ребра равны между собой. Найдите длину бокового ребра.
Решение:
АО- высота. АС=АВ=АЕ=AD, то DO=OВ=ОС=ОЕ, поэтому точка О- центр окружности описанной около параллелограмма BCDE. Но тогда параллелограмм является параллелограммом, диагонали которого пересекаются в точке О и равны друг другу.� � BCDE- прямоугольник.
� BCDE- прямоугольник.
Из ∆BDC по теореме Пифагора � �, DB=�
�, DB=� �=10 см., следовательно АО= 5 см
�=10 см., следовательно АО= 5 см
АО� �DBC. ∆АОD- прямоугольный, по теореме Пифагора �
�DBC. ∆АОD- прямоугольный, по теореме Пифагора � �, АD=�
�, АD=� �=13 см.
�=13 см.
Ответ: 13 см
Задача №2. Сторона основания правильной треугольной пирамиды 6 см, а боковое ребро 4 см. Найдите высоту пирамиды и апофему.
Решение:
Апофема- высота боковой грани правильной пирамиды. Все боковые ребра правильной пирамиды равны друг другу , поэтому высота ED ∆АDВ является ее медианой, т.е. АЕ=ВЕ.
В прямоугольном треугольнике АDЕ DЕ=� � см.
� см.
Проведем высоту пирамиды ОD.
Рассмотрим ∆DОЕ- прямоугольный, т.к. DО� �АBC.
�АBC.
По теореме Пифагора найдем DО, � �, т.к ∆АBC- правильный, ОЕ- радиус вписанной окружности, ОЕ= �
�, т.к ∆АBC- правильный, ОЕ- радиус вписанной окружности, ОЕ= � � = �
� = � � см, следовательно DО = �
� см, следовательно DО = � �=2 см.
�=2 см.
Ответ: 2 см
Задача № 3. Стороны оснований правильной усеченной четырехугольной пирамиды равны 2 м и 8 м. Боковое ребро равно 5 м. Найдите высоту пирамиды.
Решение:
АА1С1 С- равнобокая трапеция. А1С1 и АС- диагонали соответственно верхнего и нижнего основания пирамиды. А1С1=2� � см, АС= 8�
� см, АС= 8� � см (как диагонали квадрата).
� см (как диагонали квадрата).
Проведем высоты А1Е и С1К. АЕ=КС=(АС- А1С1)/2=(8� �)/2=3�
�)/2=3� � см.
� см.
∆А А1Е- прямоугольный, по теореме Пифагора найдем А1Е.
А1Е=�� см.
Ответ:� � см
� см
ТЕЛА ВРАЩЕНИЯ. ЦИЛИНДР.
Тела вращения: цилиндр, конус, усеченный конус, шар, сфера.
Определение. Цилиндром называется тело, которое состоит из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.
Цилиндр может быть получен вращением прямоугольника вокруг одной из его сторон.

прямая OO` - ось цилиндра
отрезок OO`- высота,
отрезок АА`= ВВ` - образующая
круг (О,ОВ) =кругу (O`, O`В`) – основание цилиндра
Если секущая плоскость цилиндра проходит через ось цилиндра, то сечение представляет собой прямоугольник, две стороны которого образующие, а две другие- диаметры оснований цилиндра. Такое сечение называется осевым .
Определение. Цилиндр называется равносторонним, если осевое сечение является квадратом.
Если секущая плоскость перпендикулярна оси цилиндра, то сечение является кругом.
Теорема. Плоскость, параллельная плоскости основания цилиндра, пересекает его боковую поверхность по окружности, равной окружности основания.
Задача №1. Высота цилиндра равна 8 см, радиус равен 5 см. Найдите площадь сечения цилиндра плоскостью, параллельной его оси, если расстояние между этой плоскостью и осью цилиндра равно 3 см.
Решение:
А1В1ВА- прямоугольник. Из ∆АСО по теореме Пифагора АС=� �
�
AС=� �, AB=2�
�, AB=2� �
�
S=AB∙H=� �=2�
�=2� �∙8=16∙4=64 см2
�∙8=16∙4=64 см2
Ответ: 64 см2
Задача №2. Осевое сечение цилиндра – квадрат, диагональ которого равна 20 см. Найдите: а) высоту цилиндра; б) площадь основания цилиндра.
Решение:
AA1B1B – квадрат, AB1 = 20 см, AB = H; � �
�
�� �� (см2).
Ответ:� � (см2).
� (см2).
КОНУС.
Определение. Конусом (круговым конусом), называется тело, которое состоит из круга- основания конуса, точки, не лежащей в плоскости этого круга- вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания- образующие конуса.
Определение Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания.
Конус может быть получен вращением прямоугольного треугольника вокруг одного из катетов.
т. S – вершина конуса
круг (О,ОА) – основание конуса
SA=SB – образующие конуса
Отрезок SO – высота конуса
Прямая SO – ось конуса
Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны являются образующими конуса.
Теорема. Плоскость, параллельная плоскости основания конуса, пересекает конус по кругу, а боковую поверхность - по окружности с центром на оси конуса
Возьмем произвольный конус и проведем секущую плоскость, перпендикулярную его оси. Эта плоскость пересекается с конусом по кругу и разбивает конус на две части. Одна из частей представляет собой конус, а другая называется усеченным конусом.
Определение. Усеченным конусом называется часть конуса, заключенная между его основанием и сечением, параллельным основанию. Основание исходного конуса и круг, полученный в сечении этого конуса плоскостью, называются основаниями усеченного конуса, а отрезок, соединяющий их центры- высотой усеченного конуса.
h — высота усеченного конуса,
r1 и r2 — радиусы основания усеченного конуса, l — образующая усеченного конуса.
Усеченный конус может быть получен вращением прямоугольной трапеции вокруг ее боковой стороны, перпендикулярной к основаниям.
Осевым сечением усеченного конуса является равнобокая трапеция.
Задача №1. Высота конуса равна 15 см2, а радиус основания равен 8 см. Найдите образующую конуса.
Решение:
Из ∆РОВ по теореме Пифагора � �
�
Ответ:� �
�
Задача № 2. Образующая конуса, равная 12 см, наклонена к плоскости основания под углом . Найдите площадь основания конуса, если = 30.
Решение:
SOB – прямоугольный, в нем катеты – SO, OB, гипотенуза – SB, = cos30 , ОВ = R (радиус основания) ОВ= SB∙ � � = 6�
� = 6� � см.
� см.
В основании конуса лежит круг: S=R, S = � � (см)
� (см)
Ответ:� � (см)
� (см)
Задача № 3. В усеченном конусе диагональ осевого сечения равна 10 см, радиус меньшего основания 3 см, высота 6 см. Найдите радиус большего основания.
Решение:
Осевым сечением усеченного конуса является равнобокая трапеция. ВД- диагональ данной трапеции. Из вершины В опустим высоту. ВК=ОО1=6см. По теорема Пифагора, из ∆ДВК- прямоугольный, найдем ДК. � � см. ДК=8 см. ДК=ДО1+О1К, О1К=ОВ= 3 см.
� см. ДК=8 см. ДК=ДО1+О1К, О1К=ОВ= 3 см.
Следовательно ДО1= ДК- О1К=8-3=5 см.
Ответ: 5 см.
ШАР.
Определение. Шар- тело, которое состоит из всех точек пространства, находящих на расстоянии, не больше данного, от данной точки. Точка называется центром шара, а расстояние- радиусом шара.
Граница шара называется шаровой поверхностью или сферой.
О – центр шара
ОА=ОВ – радиус шара
АВ – диаметр
Всякое сечение шара плоскостью есть круг. Плоскость, проходящая через центр шара называется диаметральной плоскостью. Сечение шара диаметральной плоскостью называется большим кругом, а сечение сферы- большой окружностью.
Теорема. Любая диаметральная плоскость шара является его плоскостью симметрии. Центр шара является его центром симметрии.
Определение. Плоскость, проходящая через точку А шаровой поверхности и перпендикулярная радиусу, проведенному в точку А, называется касательной плоскостью. Точка А называется точкой касания.
Теорема. Касательная плоскость имеет с шаром только одну общую точку- точку касания.
Прямая в касательной плоскости шара, проходящая через точку касания, называется касательной к шару в этой точке. Так как касательная плоскость имеет с шаром только одну общую точку, то касательная прямая тоже имеет с шаром только одну общую точку- точку касания.
Теорема. Линия пересечения двух сфер есть окружность.
Задача № 1. Сечение шара плоскостью имеет площадь 36(м). Радиус шара 10м. Найти расстояние от центра шара до плоскости сечения.
Решение:
1. Любое сечение шара плоскостью есть круг. S= r , где r- радиус сечения.
36 = r r= 36 (м), r = 6 см.
2. ОО’ Х – прямоугольный
( ОО’ )= OX- O’X - по т. Пифагора
( ОО’ )=100 – 36 =64, ОО’ = 8 м
Ответ: 8 м
Задача № 2. Отрезок, соединяющий центр шара с точкой А касательной плоскости, равен 17 см. Радиус шара 8 см. Найдите расстояние от точки А до точки касания шара с плоскостью и от точки А до ближайшей к ней точки шара.
Решение.
АК � �ОК. По теореме Пифагора из треугольника ОАК: АК2 = АО2 – ОК2, АК = �
�ОК. По теореме Пифагора из треугольника ОАК: АК2 = АО2 – ОК2, АК = � �= 15 . AM - ближайшее расстояние от точки А до сферы,
�= 15 . AM - ближайшее расстояние от точки А до сферы,
AM = АО-ОМ = 17 – 8 = 9 см.
Ответ: 9. см
ПРАКТИЧЕСКАЯ РАБОТА на тему «Многогранники».
№ 1. Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 0,7 см и 2,4 см, боковое ребро призмы равно 10 см. Найдите площадь боковой и полной поверхности призмы.
№ 2. Стороны оснований правильной усеченной треугольной пирамиды 1 дм и 4 дм. Боковое ребро равно 2 дм. Найдите высоту пирамиды.
№ 3. Основание пирамиды - прямоугольник со сторонами 6 см и 8 см. каждое боковое ребро пирамиды равно 13 см. Вычислите высоту.
ПРАКТИЧЕСКАЯ РАБОТА на тему «Тела вращения»
№ 1. Радиус основания конуса равен 10 см, а высота 15 см. Найдите площадь сечения конуса плоскостью, параллельной основанию и находящейся на расстоянии 2 см от его вершины.
№ 2. Высота цилиндра равна 10 дм. Площадь сечения цилиндра плоскостью, параллельной оси цилиндра и удаленной на 9 дм от нее, равна 240 дм2. Найдите радиус цилиндра.
№ 3.
Дано: ОО1=5 см, ОР=13 см.
Найдите площадь сечения шара плоскостью.
ПРАКТИЧЕСКАЯ РАБОТА на тему «Многогранники».
№ 1. Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 0,7 см и 2,4 см, боковое ребро призмы равно 10 см. Найдите площадь боковой и полной поверхности призмы.
№ 2. Стороны оснований правильной усеченной треугольной пирамиды 1 дм и 4 дм. Боковое ребро равно 2 дм. Найдите высоту пирамиды.
№ 3. Основание пирамиды - прямоугольник со сторонами 6 см и 8 см. каждое боковое ребро пирамиды равно 13 см. Вычислите высоту.
ПРАКТИЧЕСКАЯ РАБОТА на тему «Тела вращения»
№ 1. Радиус основания конуса равен 10 см, а высота 15 см. Найдите площадь сечения конуса плоскостью, параллельной основанию и находящейся на расстоянии 2 см от его вершины.
№ 2. Высота цилиндра равна 10 дм. Площадь сечения цилиндра плоскостью, параллельной оси цилиндра и удаленной на 9 дм от нее, равна 240 дм2. Найдите радиус цилиндра.
№ 3.
Дано: ОО1=5 см, ОР=13 см.
Найдите площадь сечения шара плоскостью.











 РИЗМА
РИЗМА пределение. Прямая призма называется правильной, если ее основания являются правильными многоугольниками.
пределение. Прямая призма называется правильной, если ее основания являются правильными многоугольниками.




 спользуя свойство – диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам, найдем сторону .
спользуя свойство – диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам, найдем сторону . 












