Конспект – лекция по теме : Определители II и III порядков. Решение систем двух (трех) уравнений по формуле Крамера.
Определение 1. Матрицей называется прямоугольная таблица чисел.
А = 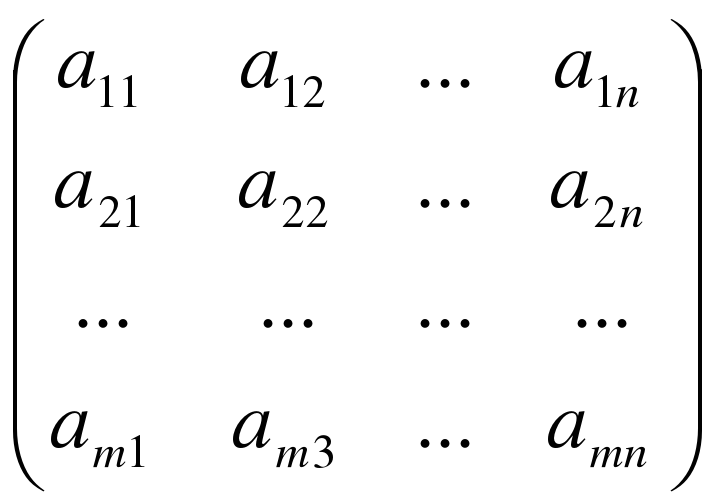
Обозначения: А – матрица, аij - элемент матрицы, i - номер строки, в которой стоит данный элемент, j - номер соответствующего столбца; m – число строк матрицы, n – число ее столбцов.
Определение 2. Числа m и n называются размерностями матрицы.
Определение 3. Матрица называется квадратной, если m = n. Число n в этом случае называют порядком квадратной матрицы.
Каждой квадратной матрице можно поставить в соответствие число, определяемое единственным образом с использованием всех элементов матрицы. Это число называется определителем.
Определение4. Определителем второго порядка называется число, полученное с помощью элементов квадратной матрицы 2-го порядка следующим образом:

При этом из произведения элементов, стоящих на так называемой главной диагонали матрицы (идущей из левого верхнего в правый нижний угол) вычитается произведение элементов, находящихся на второй, или побочной, диагонали.
Примеры.
1) 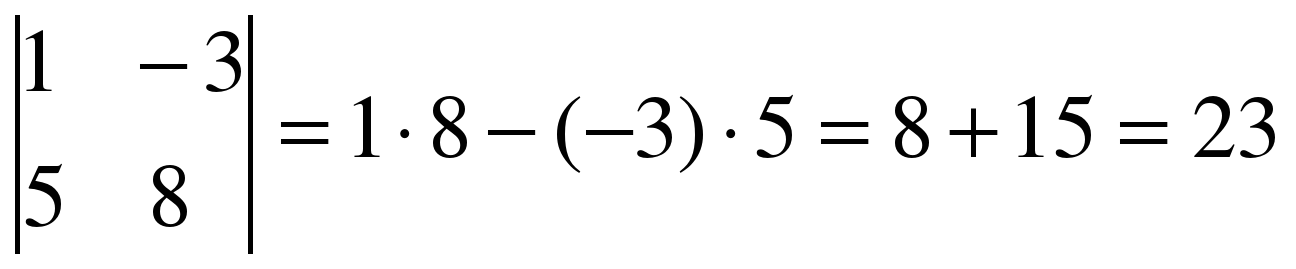 2)
2) 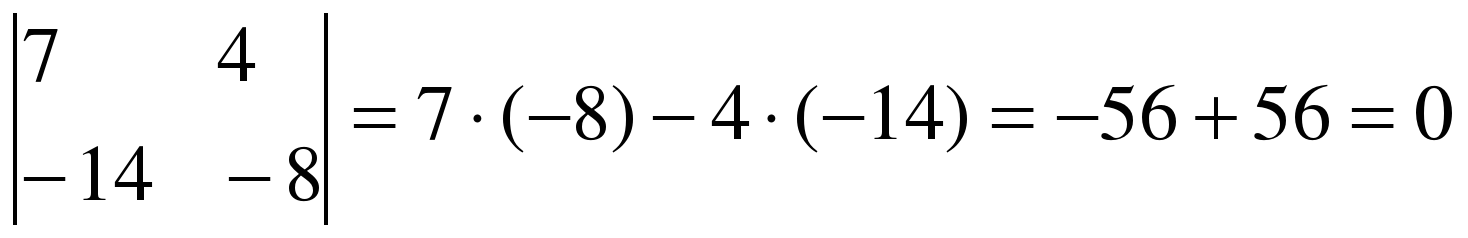
Определение 5. Определителем третьего порядка называется число, определяемое с помощью элементов квадратной матрицы 3-го порядка следующим образом:
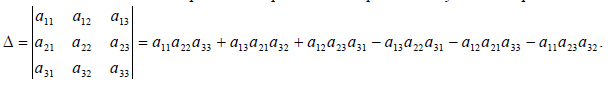
Замечание. Для того, чтобы легче запомнить эту формулу, можно использовать так называемое правило треугольников. Оно заключается в следующем: элементы, произведения которых входят в определитель со знаком «+», располагаются так:
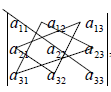
образуя два треугольника, симметричных относительно главной диагонали. Элементы, произведения которых входят в определитель со знаком «-» , располагаются аналогичным образом относительно побочной диагонали:
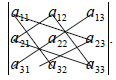
Примеры:
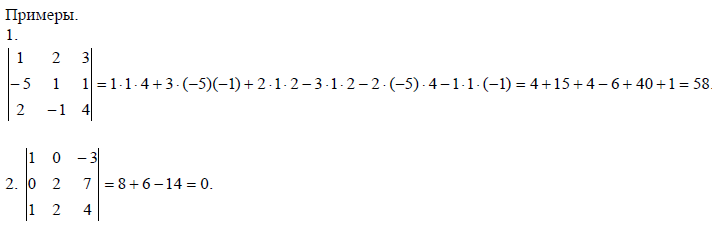
Свойства определителей
1. Определитель не меняется при транспонировании.
2. Если одна из строк определителя состоит из нулей, то определитель равен нулю.
3. Если в определителе переставить две строки, определитель поменяет знак.
4. Определитель, содержащий две одинаковые строки, равен нулю.
5. Если все элементы некоторой строки определителя умножить на некоторое число k, то сам определитель умножится на k.
6. Определитель, содержащий две пропорциональные строки, равен нулю.
7. Если все элементы i-й строки определителя представлены в виде суммы двух слагаемых ai j = bj + cj (j=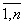 ), то определитель равен сумме определителей, у которых все строки, кроме i-ой, - такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов bj, в другом - из элементов cj.
), то определитель равен сумме определителей, у которых все строки, кроме i-ой, - такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов bj, в другом - из элементов cj.
8. Определитель не меняется, если к элементам одной из его строк прибавляются соответствующие элементы другой строки, умноженные на одно и то же число.
Замечание. Все свойства остаются справедливыми, если вместо строк взять столбцы.
Метод Крамера.
(Габриель Крамер (1704-1752) швейцарский математик)
Данный метод также применим только в случае систем линейных уравнений, где число переменных совпадает с числом уравнений. Кроме того, необходимо ввести ограничения на коэффициенты системы. Необходимо, чтобы все уравнения были линейно независимы, т.е. ни одно уравнение не являлось бы линейной комбинацией остальных.
Для этого необходимо, чтобы определитель матрицы системы не равнялся 0.
Действительно, если какое- либо уравнение системы есть линейная комбинация остальных, то если к элементам какой- либо строки прибавить элементы другой, умноженные на какое- либо число, с помощью линейных преобразований можно получить нулевую строку. Определитель в этом случае будет равен нулю.
Теорема (Правило Крамера). Система из n уравнений с n неизвестными
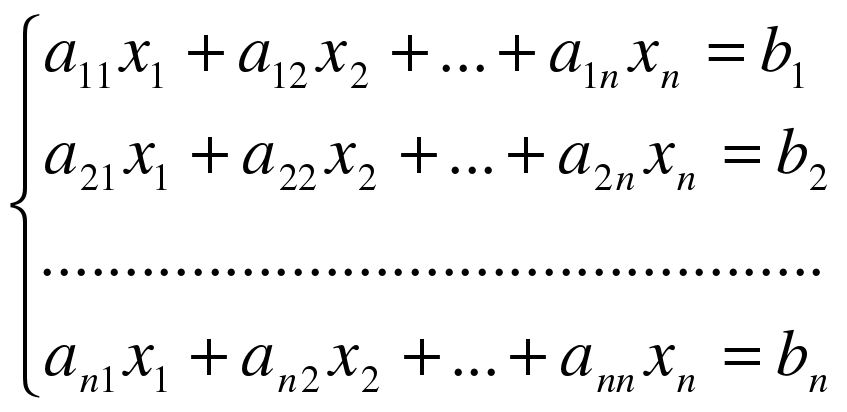
в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:
xi = 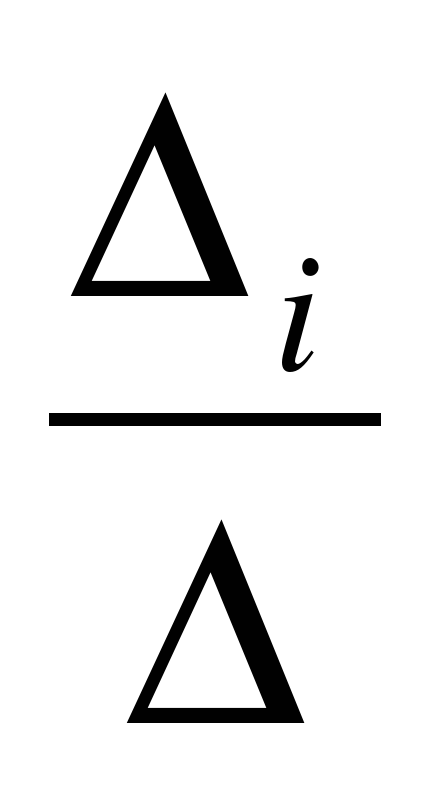 , где
, где
= det A, а i – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов bi.
Пример.
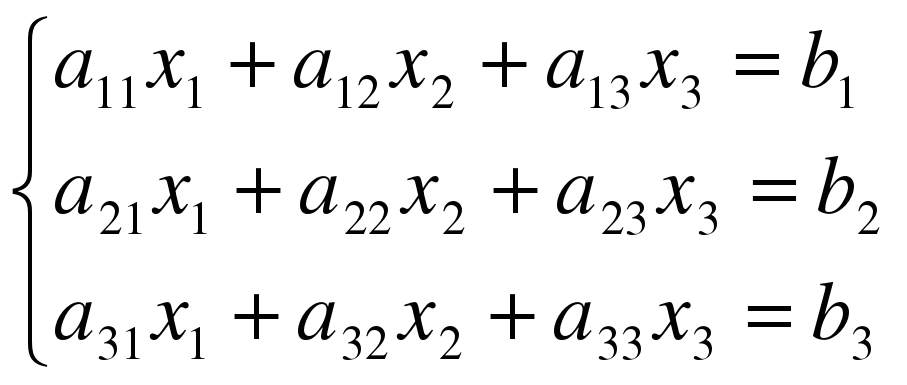
A =  ; 1=
; 1= 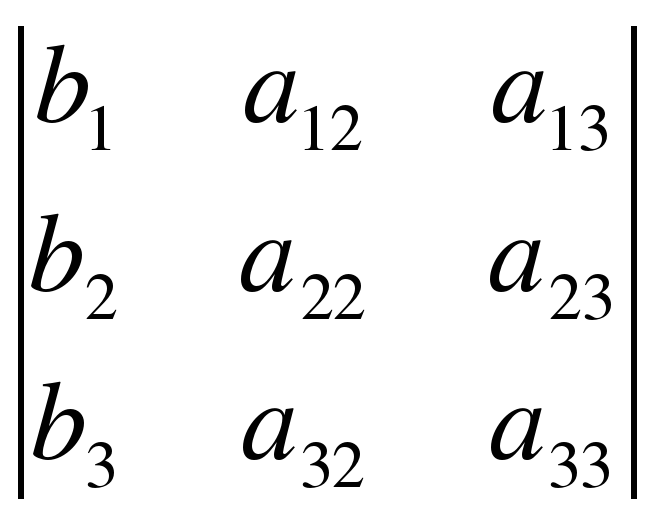 ; 2=
; 2= 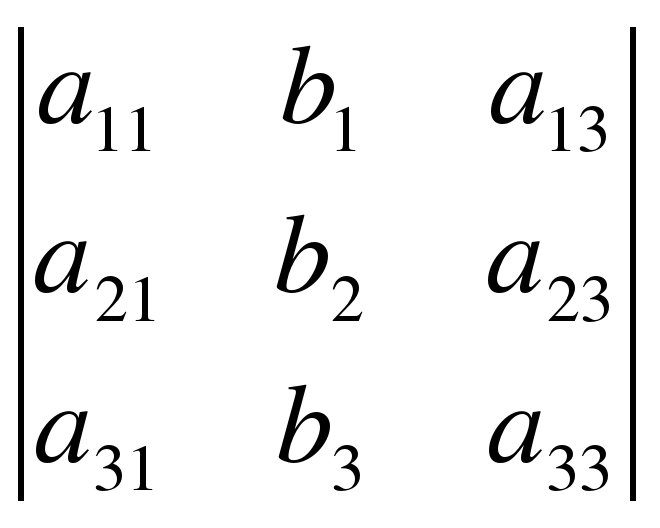 ; 3=
; 3= 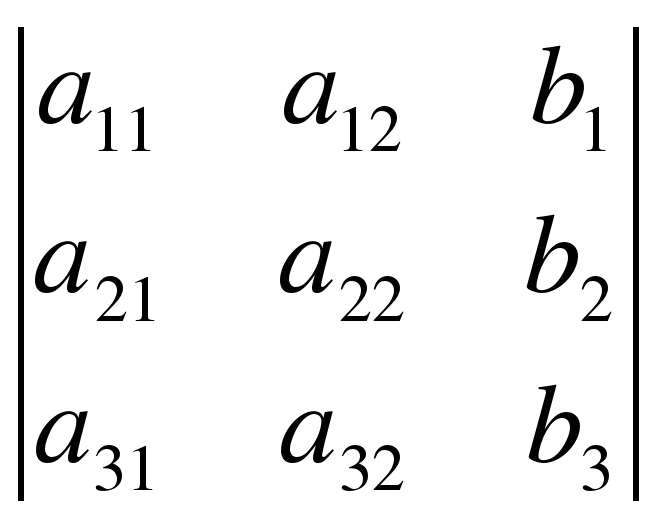 ;
;
x1 = 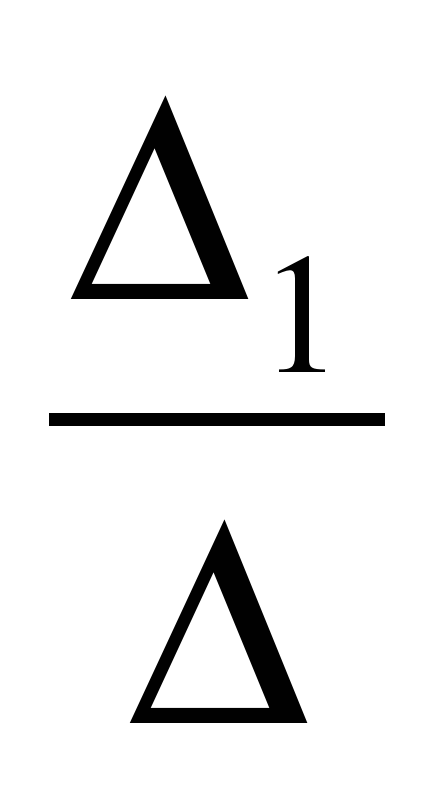 ; x2 =
; x2 = 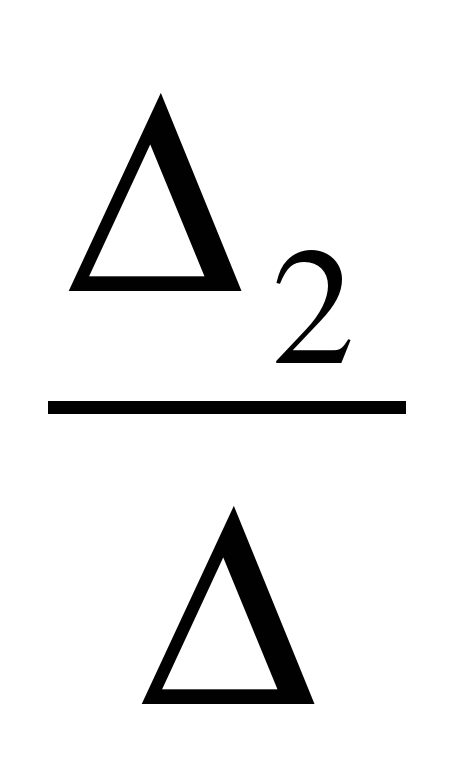 ; x3 =
; x3 = 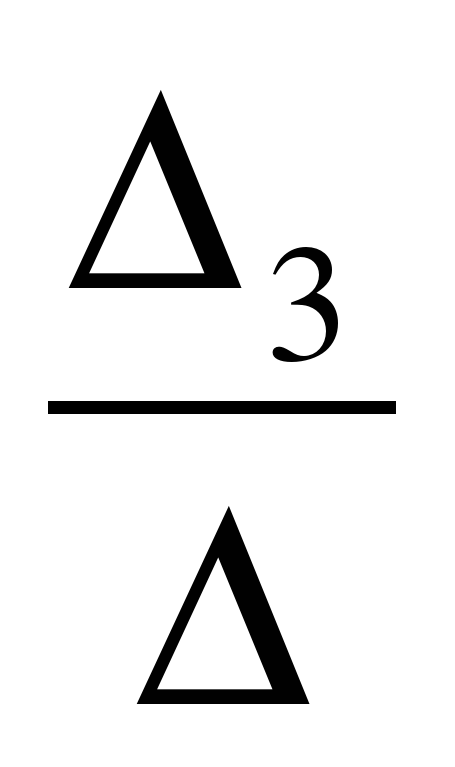 .
.
Пример. Найти решение системы уравнений:
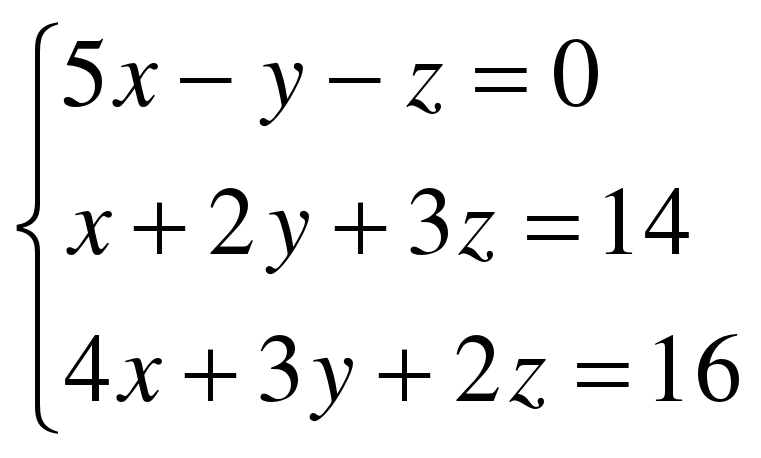
=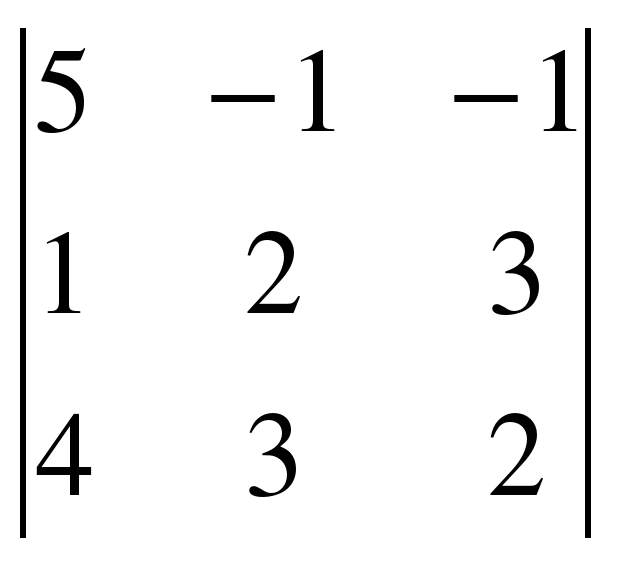 = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
= 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
Заменим первый столбец, столбцом свободных членов. Получим:
1 = 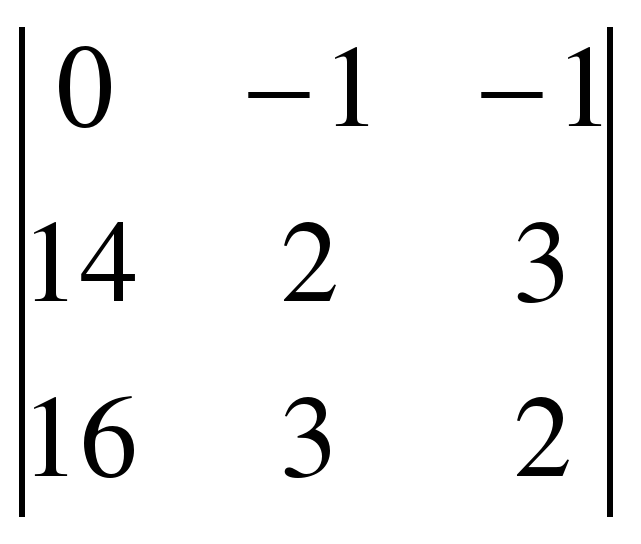 = (28 – 48) – (42 – 32) = -20 – 10 = -30.
= (28 – 48) – (42 – 32) = -20 – 10 = -30.
Заменим второй столбец, столбцом свободных членов. Получим:
2 = 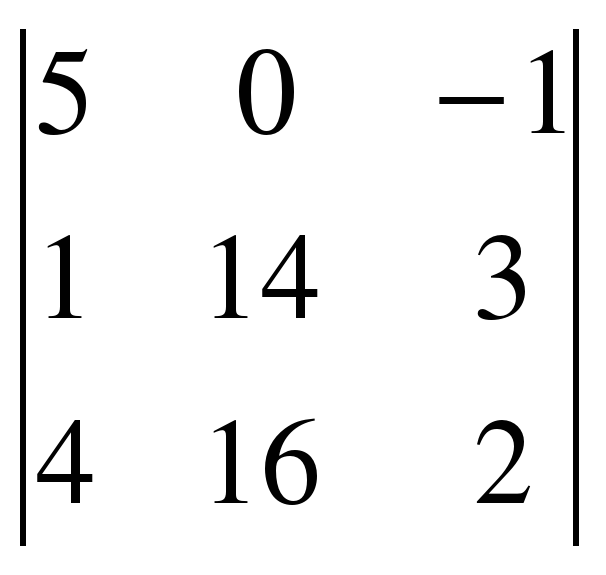 = 5(28 – 48) – (16 – 56) = -100 + 40 = -60.
= 5(28 – 48) – (16 – 56) = -100 + 40 = -60.
Заменим третий столбец, столбцом свободных членов. Получим:
3 = 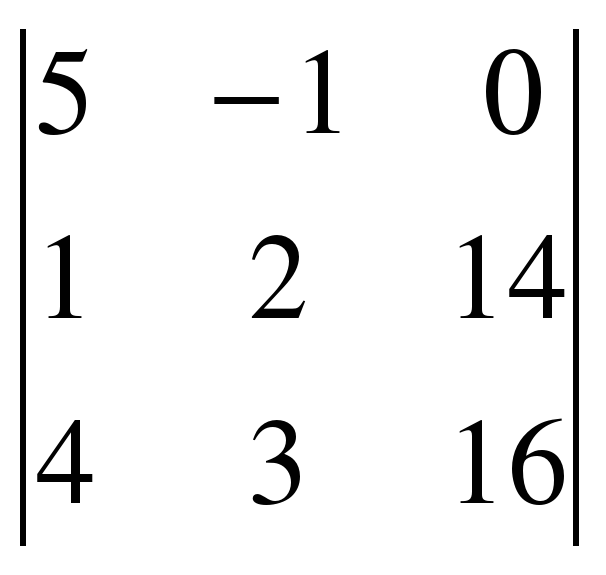 = 5( 32 – 42) + (16 – 56) = -50 – 40 = -90.
= 5( 32 – 42) + (16 – 56) = -50 – 40 = -90.
x1 =  = 1; x2 =
= 1; x2 = 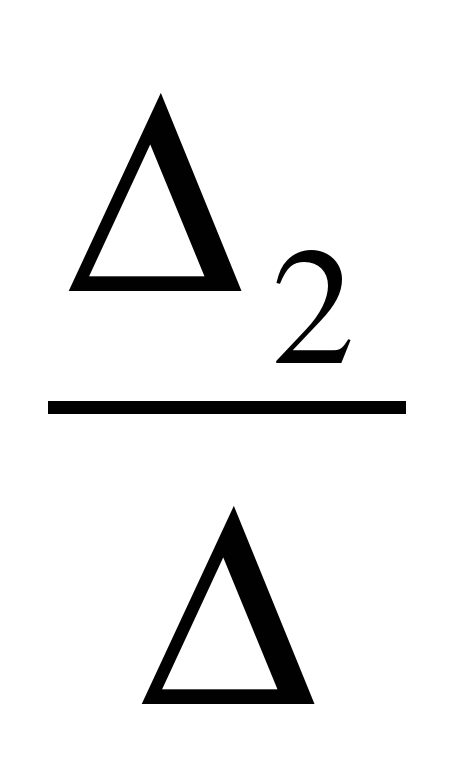 = 2; x3 =
= 2; x3 =  = 3.
= 3.
Ответ: x1 = 1; x2 = 2; x3 = 3.
Если система однородна, т.е. bi = 0, то при 0 система имеет единственное нулевое решение
x1 = x2 = … = xn = 0.
При = 0 система имеет бесконечное множество решений.
ПРАКТИЧЕСКАЯ РАБОТА
по теме «Определители II и III порядков. Решение систем двух (трех) уравнений по формуле Крамера»
№ 1. Вычислите определитель второго порядка:
а) ;
б)
№ 2. Вычислить определитель матрицы третьего порядка А =
№ 3. Найти решение системы уравнений по формулам Крамера:
№ 4. Найти решение системы уравнений по формулам Крамера: ;
Ответы и решения
№ 1 а) ==5-9= -4; б) ==5+9=14
№ 2. Ответ: А=19
№ 3.
№ 4. Ответ: x = 0; y = 0; z = -2.






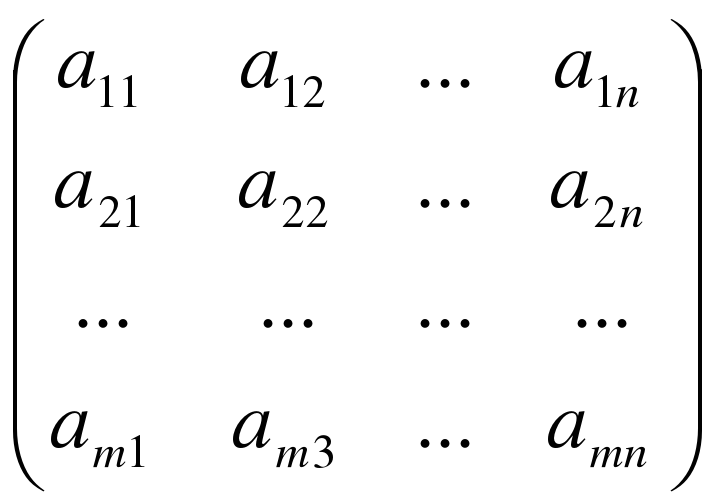

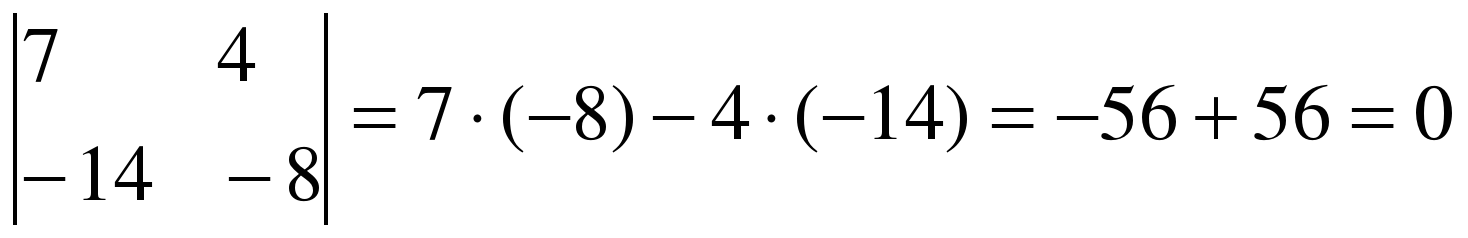
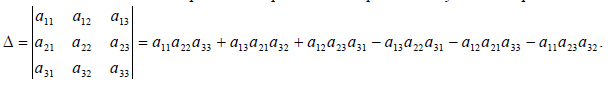
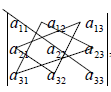

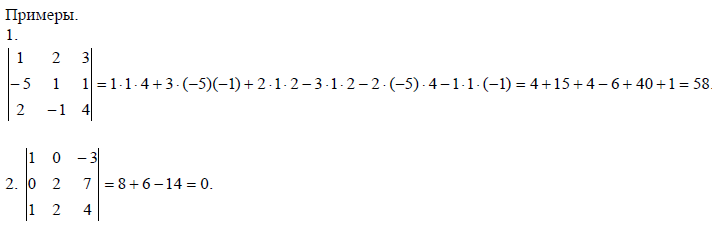
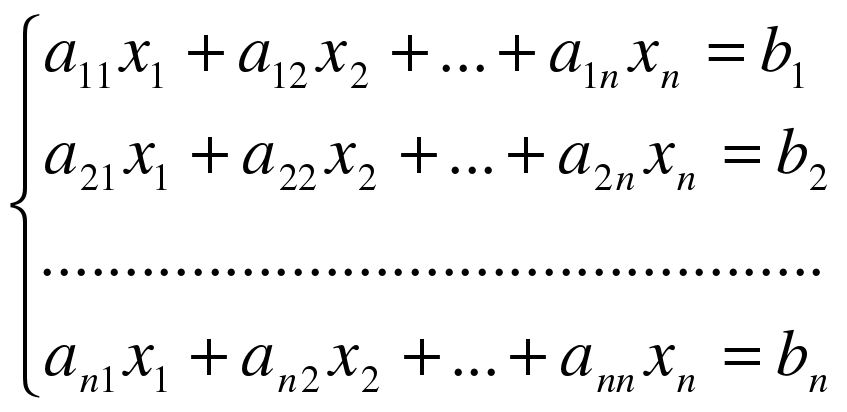
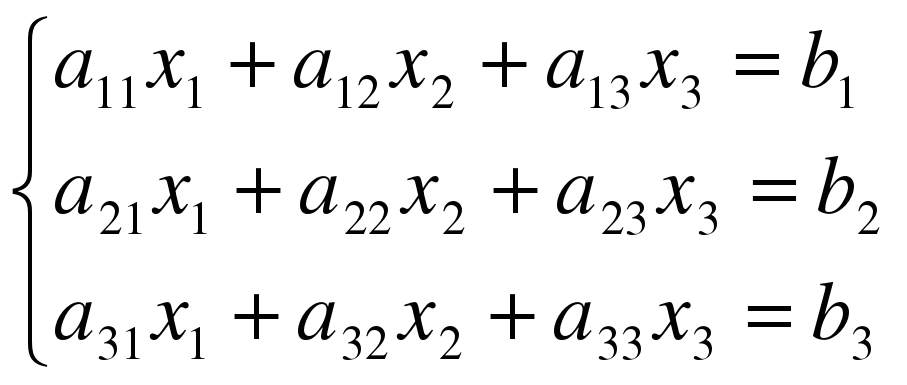
 ; 1=
; 1= 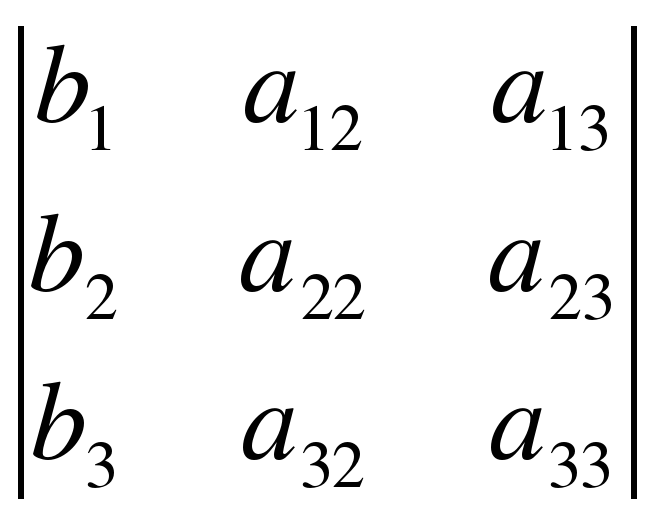 ; 2=
; 2= 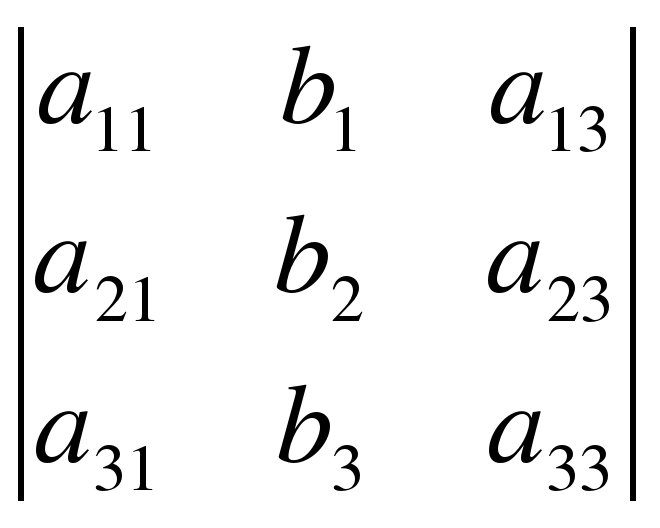 ; 3=
; 3= 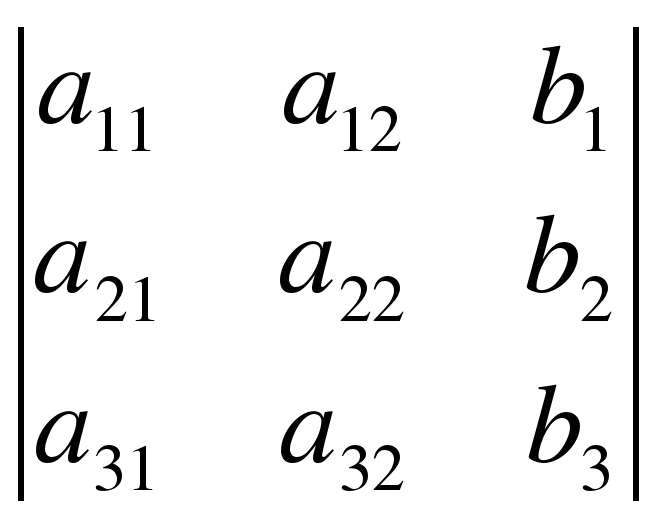 ;
;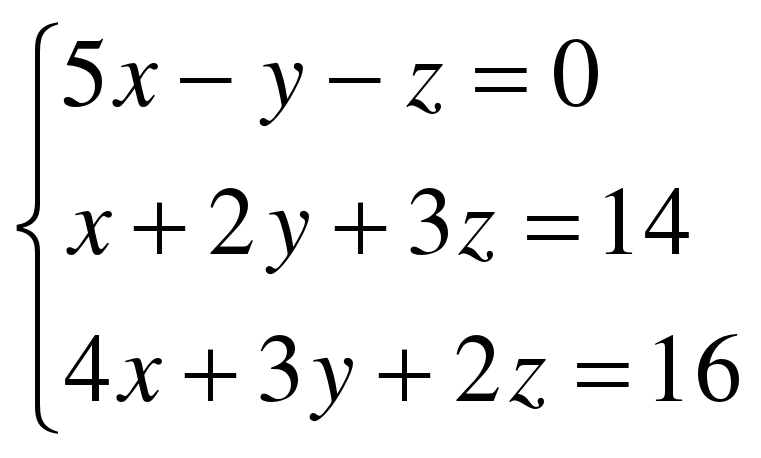
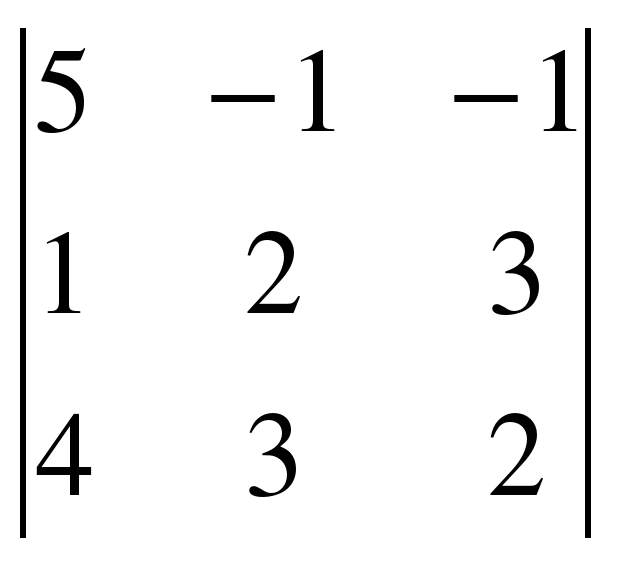 = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
= 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;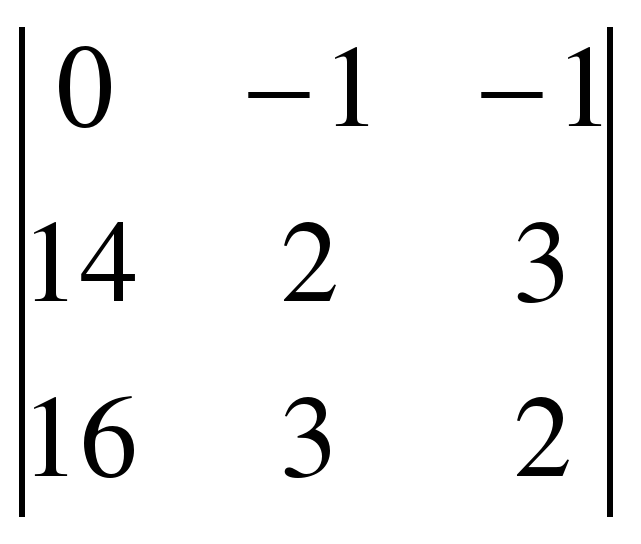 = (28 – 48) – (42 – 32) = -20 – 10 = -30.
= (28 – 48) – (42 – 32) = -20 – 10 = -30. = 5(28 – 48) – (16 – 56) = -100 + 40 = -60.
= 5(28 – 48) – (16 – 56) = -100 + 40 = -60. = 5( 32 – 42) + (16 – 56) = -50 – 40 = -90.
= 5( 32 – 42) + (16 – 56) = -50 – 40 = -90.


















