Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии

Этапы проведения урока

Задания для учащихся, выполнение которых приведёт к достижению запланированных результатов, цель, результативность.

Форма организации учебных действий

УУД

Организационный этап.

Нацеливание учащихся – мотивация

Закончился двадцатый век.

Куда стремится человек?

Изучены космос и море,

Строенье звезд и вся Земля,

Но математиков зовет

Известный лозунг:

«Прогрессио – движение вперед»

Вступительное слово учителя:

Эта история произошла давным-давно. В древнем городе жили добрый мудрец и злой человек, который завидовал славе мудреца. И решил он придумать такой вопрос, чтобы мудрец не смог на него ответить. Пошел он на луг, поймал бабочку, сжал ее между сомкнутых ладоней и подумал: "Спрошу-ка я: о, мудрейший, какая у меня бабочка - живая или мертвая? Если он скажет, что мертвая, я раскрою ладони - бабочка улетит, а если скажет - живая, я сомкну ладони, и бабочка умрет". Так завистник и сделал: поймал бабочку, посадил ее между ладоней, отправился к мудрецу и спросил его: "Какая у меня бабочка - живая или мертвая?" Но мудрец ответил: " Все в твоих руках:"

Бывают моменты в жизни, когда руки опускаются и кажется, что ничего не получится. Тогда вспомните слова мудреца "Все в твоих руках:" и пусть эти слова будут девизом нашего урока.

-- Вы перешли к изучению одной из интересных тем алгебры 9 класса – «Числовые последовательности». Наше познание курса алгебры можно сравнить с походом в горы и сегодня мы с вами преодолеем ещё одну математическую вершину, а какую вы узнаете позже. А теперь давайте проверим, готовы ли вы к восхождению.

Учащимся выдан лист рефлексии, они заполняют Ф. И.

 Личностные:

формирование мотивации, развитие познавательного интереса

Актуализация опорных знаний. Теоретический опрос

Ребята, предыдущие два урока алгебры были посвящены теме «Последовательности».

1.Что называется числовой последовательностью?

2. Приведите примеры числовых последовательностей.

3. Каким способом можно задать последовательность?

4. Какие члены последовательности (bn) расположены между

B₁₃₄ и b₁₄₂ , bn -1 и bn + 2, bn +3 и bn +6 ?

5. Последовательность задана формулой :

a_n = 3n – 3.

Найдите: α ₅, α₁₀, αk .(Ответы: 12,27, 3k-3)

6. с₁ = - 10, сn+1 = сn + 10. Найдите : с₂, с₃, с₄. (ответы 0,10,20)

Вспоминают прошлый урок и отвечают (фронтальная работа)

коммуникативные

работа с информацией.

Развивать умение грамотно излагать свои мысли, понимать смысл поставленной задачи.

Устная работа. Создание проблемной ситуации, постановка темы и целей урока.

На доске записаны последовательности:

а) 4; 8; 12; … 16,20,24

г) 1; 2; 3; 4; …5,6,7,8

б) - 13; - 15; - 17; - 19; …-21,-23,-25

д) 2; 4; 6; 8; …10,12,14

в) - 2; -4; - 8; -16; …-32,-64,-128

Продолжите их.

Какие последовательности образованы с помощью одного и того же правила? (а,б,г,д)

Определение: Числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом, называется арифметической прогрессией.

Как проверить, является ли последовательность арифметической прогрессией?

Если разность между последующим и предыдущим членами последовательности есть одно и тоже число, то данная последовательность является арифметической прогрессией

Учащиеся выполняют решение предложенных заданий .

(Учащиеся пытаются сформулировать определения самостоятельно)

Личностные:

творчество

Осуществлять анализ, синтез, проводить сравнение и классификацию по заданным критериям.

Что же нам нужно для упрощения и рационализации этой работы?

Итак: О чем пойдет речь сегодня на уроке?

Какие цели мы должны поставить и реализовать на уроке?

«Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии».

• И наша цель сегодня на уроке: используя определение арифметической прогрессии, находить любой член прогрессии , разность , порядковые номера членов арифметической прогрессии и свойство арифметической прогрессии, активировать умственную деятельность, развивать критическое мышление, научиться оценивать свои знания.

• Результативность: формирование познавательной компетентности.

• А сейчас мы снова сформулируем определение, которое у нас получилось и запишем её в виде рекуррентной формулы:

Это наша формула –по определению

a_n+1 = α_n + d, d – некоторое число

Выразим d , получим формулу d = α_n+1 – α_n,

верную при любом значении n, она выражает разность арифметической прогрессии, обозначенная d.

Т.Е. если у нас известно а₁ и d , то легко определить любой член прогрессии по схеме:

а₁ (+d) _, а₂ (+d) _, а₃ (+d) _, а₄(+d) _, а₅(+d) _……… а_n-1 (+d), а _n(+d), а_n-2 (+d) _……

Все формулируют тему и цели урока.

Записывают тему урока в тетрадях.

 Личностные:

формирование мотивации,

развитие познавательного

интереса.

Первичное закрепление нового материала

Решить устно:

1.Назовите первые пять членов арифметической прогрессии:

Разбить на три группы по рядам:

1 вариант а) α₁ = 5, d = 4; Ответы: а₁=5, а₂= 9, а₃ = 15, а₄=19, а₅=23

2 вариант. б) α₁ = 5, d = - 2 Ответы: а₁=5, а₂= 3, а₃ =1 , а₄=-1, а₅=-3.

3 вариант в) α₁ = 5, d = 0. Ответы: а ₁=5, а₂= 5, а₃ = 5, а₄=5, а₅=5

Самостоятельная работа №2- ответы занести в бланк.

Дано: (аn)- арифметическая прогрессия.

1 вариант а) а₁ = 2, а₂= 6. Найти: d . Ответ: d = 4

2 вариант б) а₃ = 8, а₄= 5. Найти: d . Ответ: d = -3

3 вариант в) а₇ = 12, а₈ = -2. Найти: d . Ответ: d = -14

Работа в группах

Регулятивные: целеполагание, действия по образцу

коммуникативные

работа с информацией,

работа в коллективе, в группе

мотивация

Если предложить вашему вниманию такую задачу : а₁ = 4, d = 1/2, а найти надо а₁₀ , а_15, а_{100. и т.д..}

Очень неудобно вычислять подряд 10 членов прогрессии, затем 15 членов и тем более 100-ый член арифметической прогрессии. Может, есть другой?

Учащиеся предлагают свои решения и способы.

Личностные:

формирование мотивации, развитие познавательного

интереса

Исследовательская работа в группах по выводу формулы

Сейчас вы попробуете самостоятельно вывести некую формулу для вычисления n-члена арифметической прогрессии.

Вывод формулы n-го члена арифметической прогрессии

( вывод формулы провести на доске с помощью учащимися

Дано: (а_n) – арифметическая прогрессия, a₁- первый член прогрессии, d – разность.

• a₂ = a₁ + d

• a₃ = a₂ + d =(a₁ + d) + d = a₁+2d

• a₄ = a₃ + d =(a₁+2d) +d = a₁+3d

• a₅ = a₄ + d =(a₁+3d) +d = a₁+4d

• . . .

• a_n = a₁+ (n-1)d

Записать в тетрадь формулу: a_n = a₁+ d (n-1)

Коллективная совместная работа по выводу формулы.

1-й ученик

2-й ученик

3-й ученик

4-й ученик

Сравнивают конечные результаты и делают вывод.

Познавательные:

проведение

анализа.

Использовать знаково – символьные средства при решении учебных задач. (П)

Анализ:

открытие нового способа действий.

Создание проблемной ситуации,

Заметим , что эту формулу можно записать иначе:

a_n = a₁+ d (n-1)

a_n = a₁+ dn-d

a_n = dn+( a₁-d),

обозначим d через k , а разность ( a₁-d) через b, получим:

a_n=kn+b, где k и b некоторые числа

Таким образом, можно определить любой член арифметической прогрессии.

Но, есть и другие задачи, когда нужно определить, является ли данное число членом заданной арифметической прогрессии.

Содержит ли арифметическая прогрессия : 17; 13; 9 ; 5 число:

а)-7, б) -5

Решение:

а₁=17, a_n = a₁+ d (n-1) a_n = a₁+ d (n-1)

d= -4 17-4(n-1)= -7 17-4(n-1)= -5

а_n=-7 -4n = -28 -4n = -26

n= 7 n= -26/5

при n=7 (натур.число), следует, что а₇= -7. Другой ответ не подходит, т.к. индексом не может дробное число.

Учащиеся вместе с учителем выводят новые формулы.

Совместноерешение задачи у доски.

Познавательные:

Освоение нового способа деятельности.

Применение способов действий (формул) к новым ситуациям

Вторичное закрепление материала

Самостоятельное решение с последующей проверкой.(на белой доске решают два ученика)

№ 575 (а, б),

Комментированное решение с места

№ 576 (b₇= b₁ +6d , …….. b_2k = b₁+d(2k-1)

Решить у доски:

№ 577 ( а) с₅= с₁ +4d = 20+4*3=32

Самостоятельная работа №3 –ответы занести в бланк.

1.Дано: (аn)- арифметическая прогрессия,

1 Вариант а) а₁ = 4, а₃ = 6. Найти: а₂ ответ: 5

2 Вариант б) а₃ = -5, а₅ = 5. Найти: а₄ ответ: 0

3 Вариант в) а₇ = 10, а₉ = 6. Найти: а₈ ответ: 8

Индивидуальное самостоятельное решение с последующей проверкой.

Комментированное решение

Работа у доски.

Индивидуальная самостоятельная работа. Ответы заносятся в бланки-ответов.

Личностные:

Развитие креативных способностей

Физкультминутка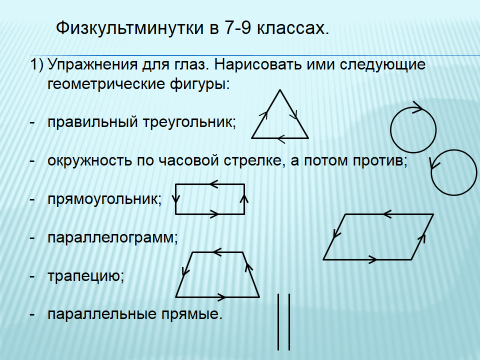

Выполнение физкультминутки

Закрепление нового материала

3.Закрепление.

№ 579 (а) ( решение у доски)

a_n = a₁+ d (n-1)

№ 591 (а) ( решение у доски) n=23

Учащиеся решают у доски (помощь учителя с затруднениями )

Личностные:

развивать находчивость, активность при решении задач.

Итог урока.

Рефлексия.

Тест по теме « Арифметическая прогрессия»

Возвращаясь к эпиграфу нашего урока, я хочу узнать, действительно ли был прав мудрец "Все в твоих руках" ?

- Что нового узнали на уроке?

- Какова формула n-го члена арифметической прогрессии? Пользуясь данной формулой что мы можем найти?

Трудным ли для вас было покорение новой математической вершины, я бы хотела узнать где вы находитесь - по-прежнему у подножия горы, на средине пути или на вершине, изобразите себя на заранее приготовленных листа.

Учащиеся записывают в бланки ответов (индивидуальная работа) и сдают учителю.

Учащиеся заполняютт лист рефлексии.

Умение адекватно оцениватьсвои знания и воспринимать оценку учителя. (Р)

Домашнее задание.

п.25 знать обе формулы определения n-члена арифметической прогрессии)

№ 575 (в.г) , № 577 ( б), № 579 (б, № 591 (б) .

Повторение: № 600(а)

Цель: проверить усвоение материала урока, формировать умение подбирать примеры

Результативность: формирование самообразовательной компетентности

 Возможность оценки достижения планируемых результатов.

 Регулятивные:

контроль, коррекция, оценка.

Формирование способности

к самосовершенствованию