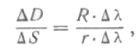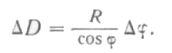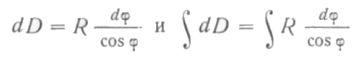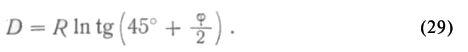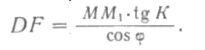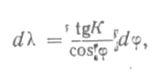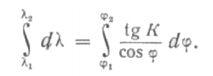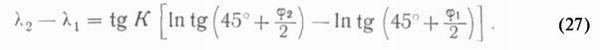Основные сведения о картографии и картографических проекциях.

Тема 1.4. Основные сведения о картографии и картографических проекциях.

План лекция № 5

1. Основные определения. Классификация картографических

проекций.

2. Проекция Меркатора.

3. Проекция Гаусса.

4. Гномоническая проекция.

Цель занятия:

Знать:

- основные определения и классификацию картографических проекций;

- достоинства и недостатки картографических проекций.

Уметь:

- различать карты по картографическим проекциям.

1. Основные определения. Классификация картографических

проекций.

При осуществлении перехода по наивыгоднейшему пути судоводителю необходимо иметь отчетливое представление о взаимном расположении пунктов отхода и прихода, о навигационных условиях, через которые проходит трасса выбранного пути, а также знать гидрометеорологическую обстановку на тот период времени, в течение которого будет проходить плавание.

Изучение районов земной поверхности, в которых предполагается плавание судов, осуществляется с помощью специальных навигационных пособий.

Наиболее распространенным видом навигационных пособий являются морские карты. Они используются для ведения навигационной прокладки, составления навигационно-гидрографических обзоров и дают разнообразные справочные сведения, необходимые судоводителю для изучения района плавания.

Карты изображают на плоскости земную поверхность или часть ее в определенном масштабе. Земля имеет сферическую форму, и изобразить ее на плоскости без искажений невозможно. Поэтому любая карта земной поверхности имеет искажения того или иного характера.

Способ условного изображения поверхности Земли на плоскости называют картографической проекцией, а полученную при этом систему меридианов и параллелей — картографической сеткой. При этом каждой точке на изображаемой поверхности соответствует однозначная точка на плоскости.

Классификация картографических проекций.

Существует много видов картографических проекций. Их можно классифицировать по следующим двум важнейшим признакам:

- по характеру искажений (по свойствам изображений), которые имеет данная карта;

- по виду меридианов и параллелей нормальной картографической сетки.

По характеру искажений проекции делят на:

- равноугольные (конформные);

- равновеликие (эквивалентные);

- произвольные виды проекций.

Равноугольные (конформные)

На картах в конформной проекции бесконечно малые фигуры изображаются подобными соответствующим фигурам на земной поверхности. Например, бесконечно малый кружок на земной поверхности изобразится на карте в равноугольной проекции также кружком. Подобие фигур обусловливает равенство соответствующих углов. Поэтому на картах в конформной проекции сохраняется равенство углов между какими-либо направлениями на местности и теми же направлениями на карте. Отсюда и название проекции — равноугольная (конформная). На картах в такой проекции невозможно сохранить эквивалентность площадей.

Равновеликие (эквивалентные)

На картах в равновеликой (эквивалентной) проекции сохраняется пропорциональность площадей соответствующим площадям на земной поверхности, но не сохраняется подобие фигур. Например, бесконечно малый кружок на земной поверхности изобразится на карте в равновеликой проекции, пропорциональным по площади эллипсом. Пропорциональность площадей сохраняется в равновеликих проекциях независимо от размеров изображаемой площади.

Произвольные

Произвольные проекции не сохраняют ни равенства углов, ни пропорциональности площадей, но они обладают особыми специальными свойствами. Из числа произвольных проекций часто выделяют равнопромежуточные проекции, обладающие промежуточными свойствами между равноугольными и равновеликими проекциями. В таких проекциях масштаб сохраняет свою величину по одному из главных направлений.

По виду меридианов и параллелей нормальной картографической сетки различают:

- конические;

- цилиндрические;

- азимутальные;

- перспективные;

- условные проекции.

При конических и цилиндрических проекциях земную поверхность проектируют по тому или иному закону на боковую поверхность касательного или секущего конуса или цилиндра, с последующей разверткой этой поверхности в плоскости. Различают нормальные, поперечные или косые конические или цилиндрические проекции в зависимости от того, совпадает ли ось конуса или цилиндра с осью Земли, с экватором или занимает некоторое промежуточное положение.

При азимутальной проекции земную поверхность проектируют на касательную к ней плоскость.

Перспективные проекции являются частным случаем азимутальных проекций и отличаются от последующих тем, что строятся по законам перспективы.

Условные проекции предполагают построение картографических сеток, исходя из тех или иных предварительно поставленных условий, исполнение которых позволяет создать проекции, обладающие необходимыми достоинствами. Таких проекций можно мыслить бесконечно большое число.

1. Проекция Меркатора.

Во время плавания необходимо вести учет движения судна в море. Для этого наиболее удобен и нагляден графический способ учета, связанный с прокладкой на карте пути судна и с построением углов, под которыми с судна наблюдают различные предметы. Поэтому к морской карте предъявляются следующие требования: 

- линия пути судна, следующего одним и тем же курсом (локсодромия), должна изображаться на карте прямой; 

- картографическая проекция должна быть равноугольной. 

Этим требованиям удовлетворяет равноугольная нормальная цилиндрическая (меркаторская) проекция. Свое второе название эта проекция получила по имени предложившего ее впервые в 1569 г. голландского ученого Кремера (Меркатора). Рассмотрим эту проекцию, 

Пусть вокруг земного шара описай цилиндр, ось которого совпадает с осью вращения Земли. Такой цилиндр (рис. 1) касается земного шара по экватору в точках EABCGFQ. Если на боковую поверхность этого цилиндра спроектировать изображения земных меридианов и параллелей, а затем его развернуть по одной из образующих, то получим нормальную цилиндрическую проекцию. На этой проекции все меридианы и параллели изображены прямыми линиями, образуя прямоугольную сетку. На такой сетке расстояния между меридианами пропорциональны разностям соответствующих им долгот, а расстояния D параллелей от экватора являются функцией широты. Исходя из требований, предъявляемых к морской карте, эта функция DI = f (φi) должна удовлетворять условиям равноугольности, т. е. конформности. 

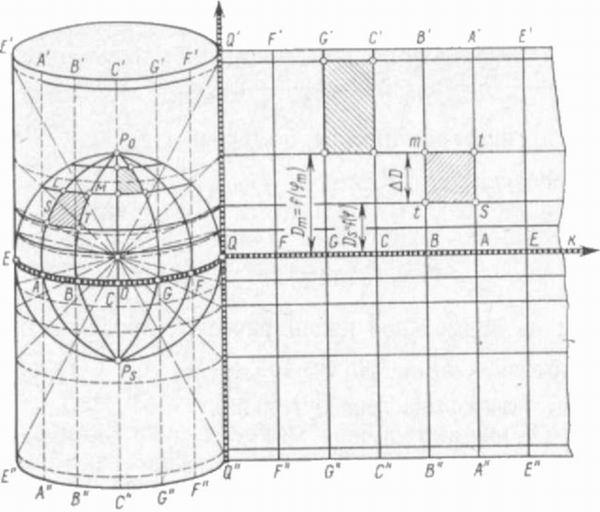
Рис. 1

Возьмем на поверхности земного шара участок LMTS (рис. 1 — сфера), образованный пересечением меридианов и параллелей, и соответствующую этому участку фигуру lmts на нормальной цилиндрической проекции. Фигуры LMTS и lmts должны быть подобными — только в этом случае проекция будет конформной. Тогда 

Определим значение сторон отмеченных фигур следующим образом: 

ТМ = AS — отрезок дуги меридиана; 

TS = rAЛ — длина дуги параллели между меридианами точек S и T (r — радиус параллели точек S и Т); 

ts = ВA = R-AЛ — длина дуги параллели на проекции, равная длине изображения дуги экватора В A (R — радиус земного шара); 

tm = AD - разность расстояния двух параллелей от экватора по меридиану. 

Тогда выражение (28) получит вид 

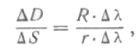
а так как r=R cos φ и АS=RAφ, то 

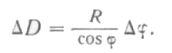
Переходя к дифференциалам, получим 

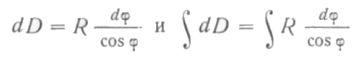
или 

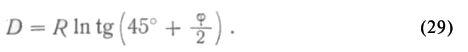
Итак, если на нормальной цилиндрической проекции параллель проводить на расстоянии 

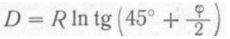
от экватора, то такая проекция будет конформна (равноугольна). 
Величину D, выраженную в минутах дуги экватора, называют меридиальной частью данной параллели. 
Уравнение прямой линии на меркаторской проекции выведем, подставляя в общий вид уравнения прямой с угловым коэффициентом вместо текущих координат их выражение через φ и λ. 
Полагая y = D = R In tg (45°+φ/2); x = Rλ (см. рис. 25), получим следующий вид уравнения прямой линии на равноугольной цилиндрической проекции: проекция будет конформна (равноугольна). 

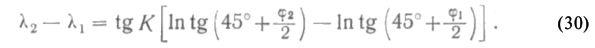
Кратчайшим расстоянием между двумя точками на земной поверхности является дуга большого круга-ортодромия , пересекающая все меридианы под разными углами. При плавании по ортодромии приходится постоянно менять курс судна, производя трудоемкие л громоздкие вычисления. Поэтому к плаванию по ортодромии прибегают только при больших океанских переходах (тысячи миль). Меньшие переходы делают постоянным курсом, линия которого на поверхности Земли представляет кривую двоякой кривизны — локсодромию. Локсодромия пересекает все меридианы под одним и тем же углом, спиралеобразно приближаясь к земному полюсу. Выведем уравнение локсодромии. 
Пусть радиус Земли равен R (рис. 2), а радиус некоторой параллели АВ — r. Тогда выражение 

определяет соотношение между длиной экватора и длиной параллели в широте φ. 
Пусть дуга М0С есть локсодромия с двумя произвольными точками на ней Mi (φ1 ,λ1) и М2 (φ2 ,λ2); К — угол пересечения локсодромии с земными меридианами. Тогда из треугольника MM1M2, который из-за малых размеров можно считать плоским и прямоугольным при вершине М, имеем 

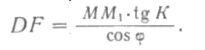
Обозначим DF = Аλ, MM1 = Аφ. Переходя к дифференциалам, получим 

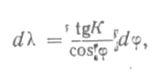
на основании чего можем записать 

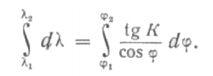
Так как tg К — постоянная величина, то уравнение локсодромии получает следующий окончательный вид: 

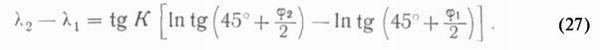
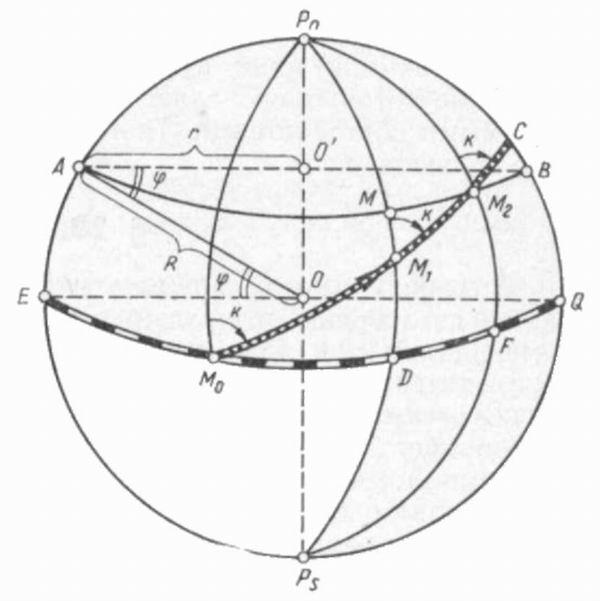
Рис. 2.

Сравнение выражений (27) и (30) показывает, что локсодромия изображается на меркаторской карте прямой линией. 

1. Проекция Гаусса.

Сущность равноугольной поперечно-цилиндрической поверхности, которая называется проекцией Гаусса, состоит в следующем.

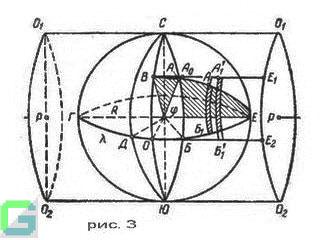
На рис. 3 изображена уровненная поверхность Земли, принимаемая в первом приближении за шар радиуса R, где северный и южный полюсы соответственно находятся в точках С и Ю. Мысленно поместим земной шар в цилиндр так, чтобы поверхность цилиндра касалась шара по некоторому меридиану ЮОВС. При этом ось цилиндра пройдет через центр шара и будет перпендикулярна плоскости меридиана касания.

На поверхности земного шара возьмем точку А, положение которой определяется географическими координатами – широтой S, равной дуге БА меридиана, проходящего через точку А, и долготой L, равной дуге ГДБ экватора.

Если через точку А и ось цилиндра РР проведем плоскость, которая в сечении на шаре образует дугу большого круга ЕАВ, перпендикулярную меридиану касания в точке В, то положение точки А может быть определено отрезками дуг больших кругов ОВ=XA и ВА=YА, которые принято называть сферическими прямоугольными координатами точки А. Если при этом будет известна долгота меридиана касания, то положение точки А на поверхности шара вполне определится.

Если дугу ОЕ экватора и дугу ВЕ большого круга ВАЕ мысленно выпрямить и совместить с поверхностью цилиндра так, чтобы они оставались перпендикулярными к меридиану касания, то эти дуги займут положение образующих цилиндра ОЕ2 и ВЕ1, а точка А сферы займет на поверхности цилиндра положение А0; при этом ее сферические координаты XА=ОВ (сферическая абсцисса) и YА=ВА=ВА0 (сферическая ордината) останутся без изменений.

Мысленно разрежем цилиндр по образующим О1О1 и О2О2, затем развернем его на плоскость. При развертке цилиндра меридиан касания СОЮ обращается в прямую линию и служит осью абсцисс, а выпрямленная дуга экватора ОЕ2 – осью ординат плоской прямоугольной системы координат. Начало этой системы координат окажется в точке О на экваторе.

На рис. 4 представлена развернутая на плоскость часть земного шара, ограниченная меридианами СДЮ и СБ0Ю, назначение которых выясним далее.

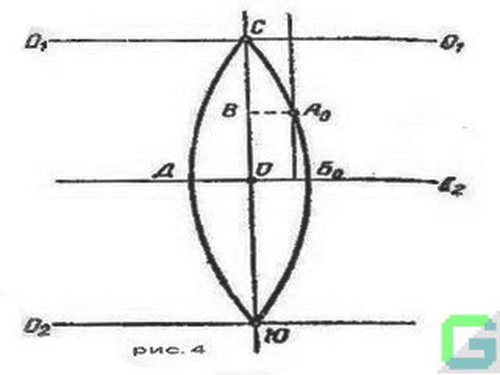
Таким образом, если нам будут известны сферические координаты некоторой точки А, то по этим координатам можно определить ее положение А0 на плоскости развернутого цилиндра.

Однако такая проекция неудобна, так как при этом не сохраняется подобие фигур. Например, элемент А1Б1 (полоска) поверхности земли при переносе с шара на цилиндр, а следовательно и на плоскость удлиняется вдоль оси абсцисс и становится равной величине А'1В'1 (рис. 3). Чтобы достигнуть подобия фигур при перенесении их с шара на плоскость, искусственно вводят искажение и по оси ординат. При этом делается это так, чтобы искажение по оси ординат было одинаковой меры с искажением по оси абсцисс данного места.

В результате такого преднамеренного увеличения размеров фигуры в направлении оси ординат, размеры ее окажутся большими в сравнении с действительными размерами на поверхности Земли.

Увеличение размеров фигур будет тем больше, чем дальше они будут расположены от меридиана касания по долготе. В высшей геодезии доказывается, что для обеспечения подобия фигур в малых частях нужно сферические ординаты точек умножать на множитель: 1 + Y2/6R2, т. е. для точки А0 (рис. 3) величина ординаты на плоскости будет :

yА = Y А (1 + Y2/6R2), (1)

где:

YА – сферическая ордината точки А на поверхности Земли;

R – радиус Земли.

Абсцисса хА точки А0 на плоскости останется равной ее сферической абсциссе ХА, т. е. хА = ХА.

Таким образом, если по оси абсцисс будем откладывать абсциссы х1 точек, равные их сферическим абсциссам Х1, а по оси ординат – ординаты, вычисленные по формуле (1), то на плоскости получим фигуры, подобные фигурам на поверхности земли, т. е. с равными углами. Такую проекцию принято называть равноугольной или конформной проекцией.

Вследствие увеличения размеров фигур при перенесении их вышеописанным способом с поверхности Земли на плоскость произойдет и увеличение длин во всех направлениях, т. е. длины на плоскости проекции окажутся больше соответствующих длин на поверхности земли, благодаря чему возникает необходимость введения специальных поправок в длины, измеренные на местности и приведенные к уровню моря.



В высшей геодезии доказывается, что поправка на увеличение длины при перенесении ее с поверхности Земли на плоскость проекции определяется в первом приближении по формуле:

dS = S y2/2R2, (2)

где:

dS – погрешность;

S – длина линии на местности;

R – радиус Земли

При удалении точек от меридиана касания на 3 град. по долготе величины поправок за искажение длин будут меньше ошибок измерения при топографических съемках. Поэтому, если ограничиться полосой поверхности Земли, заключенной между меридианами СБЮ и СДЮ (рис. 3, 4), отстоящими от меридиана касания на 3 град. долготы, то в пределах такой шестиградусной полосы или зоны нет необходимости вводить поправки при производстве мелкомасштабных топографических съемок. Благодаря этому условились при применении рассматриваемой проекции делить всю поверхность Земли меридианами на шестиградусные или трехградусные зоны по долготе. Трехградусные зоны применяются при крупномасштабных съемках.

проекция Гаусса

Для каждой зоны строится свой цилиндр, касающийся поверхности Земли по среднему меридиану зоны, который принято называть осевым меридианом. Долгота осевого меридиана для каждой зоны определяется по формуле:

6o n – 3o

(где n – номер зоны).

В каждой такой зоне начало прямоугольной системы координат будет в точке пересечения осевого меридиана с экватором.

В северном полушарии абсциссы положительны, ординаты имеют знак плюс к востоку от осевого меридиана и знак минус к западу. Иногда при составлении некоторых топографических карт ко всем ординатам прибавляется 500 км для устранения отрицательных их значений; кроме того, впереди записывается номер зоны.

Как известно, для определения взаимного положения пунктов опорной сети района съемок необходимо знать координаты хотя бы одного пункта. В высшей геодезии выводятся формулы перехода от географических координат пункта к прямоугольным плоским координатам с учетом всех искажений поперечно-цилиндрической проекции. Следовательно, для того, чтобы определить плоские прямоугольные координаты какой-либо точки поверхности Земли, нужно определить ее географические координаты, а затем обратиться к формулам высшей геодезии и вычислить по ним плоские прямоугольные координаты поперечно-цилиндрической проекции.

Такое свойство рассмотренной проекции позволило принять ее, как единую государственную систему координат.

Достоинства поперечно-цилиндрической проекции велики:

- на плоскости получается прямоугольная система координат, удобная для графических построений и для решения задач аналитическим путем.

- при производстве большинства топографических и маркшейдерских съемок нет необходимости вводить поправки в измерения за приведение их на плоскость проекции и тем осложнять вычисления.

- поперечно-цилиндрическая проекция обеспечивает возможность использования каждого плана, как составной части общего картографирования страны

4. Гномоническая проекция.

При больших океанских переходах часто прибегают к плаванию по дуге большого круга — ортодромии. Прокладка ортодромии на карте меркаторской проекции — дело сложное, требующее трудоемких предварительных вычислений. В то же время существует такая картографическая проекция, на которой дуга большого круга, а также меридианы прокладываются в виде прямой линии. Карты, выполненные в такой проекции, называемой центральной (гномонической), широко используются в морском судовождении, несмотря на то, что проекция не конформна, локсодромия на ней выглядит в виде кривой линии и с такой карты очень трудно производить снятие расстояний. 

Известно, что большой круг есть кривая, плоскость которой проходит через центр сферы, т. е. через точку зрения, поэтому любая дуга большого круга на центральной проекции изобразится обязательно только в виде прямой линии. Карты в гномонической проекции используются для расчетов плавания в открытом море по дуге большого круга, т. е. для прокладки на них ортодромических курсов и пеленгов, изображающихся на таких картах в виде прямых линий. Наглядное представление об изображении ортодромии (точечная линия) и локсодромии (сплошная линия) на гномонической а и меркаторской б проекциях дает рис.53. 

Гномоническая проекция(1) — древнейшая из всех известных, принадлежит к одному из видов азимутальных (перспективных) проекций. 

Гномоническая карта получается при проектировании земной поверхности на плоскость, касательную к ней, при условии, что глаз наблюдателя расположен в центре Земли. 

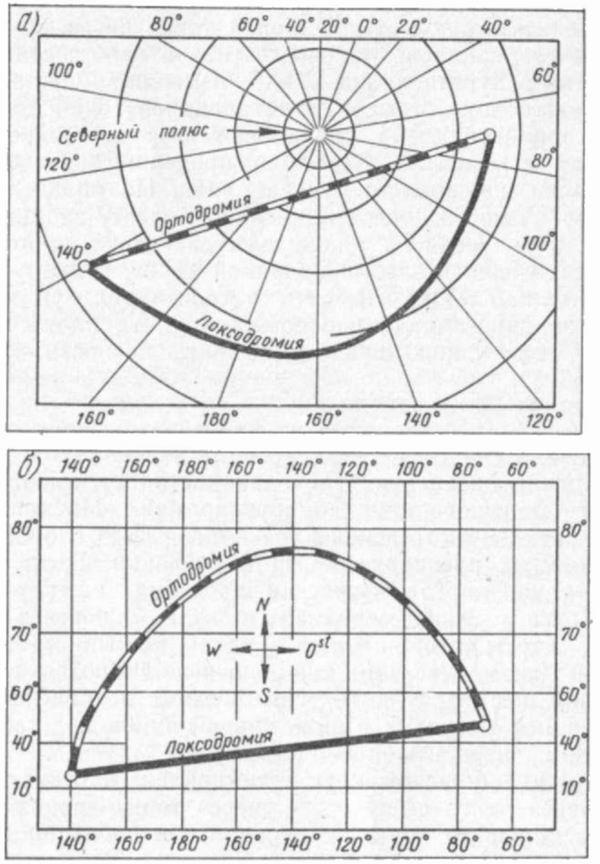
Рис. 5.

В зависимости от географического положения точки касания (центральной течки) гномонические проекции делят на три типа: 
- нормальной, прямой или полярной (рис. 6, а) называют проекцию, если центральная точка совпадает с одним из географических полюсов Земли; 
- поперечной или экваториальной (рис. 6, б) — если центральная точка находится на экваторе; 
- при горизонтальной или косой проекции (рис. 6, в) центральная точка находится между полюсами и экватором. 

Наиболее употребительны карты в нормальной (полярной) гиомонической проекции. В этой проекции, в частности, составлены карты океанов и околополярных районов земной поверхности. 

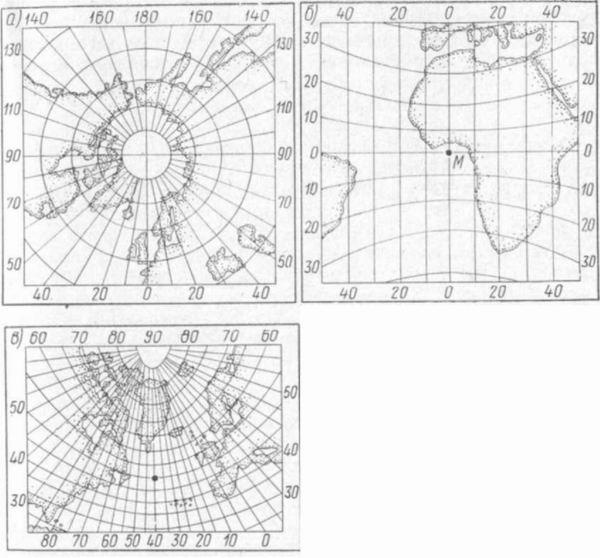
Рис. 6.

Карты в поперечной центральной проекции удобно использовать для изображений экваториальных областей звездного неба

Контрольные вопросы:

1. По виду меридианов и параллелей нормальной картографической сетки делят на?

2. Почему проекция Гаусса носит название: «Равноугольная поперечно-цилиндрическая»?

3. Как изображаются меридианы и параллели в проекции Гаусса?

4. По характеру искажений проекции делят на?

5. В чем достоинства поперечно-цилиндрической проекции?