От зеркальной симметрии к бордюрам и орнаментам

АННОТАЦИЯ

Бордюгова Ольга, Евсеева Маргарита п.Курагино, МБОУ КСОШ № 3, 8 класс

«От зеркальной симметрии к бордюрам и орнаментам».

Руководитель Юдина Ольга Ивановна, учитель математики.

Цель работы: изучение незеркальных видов симметрии.

Задачи:

1) Проанализировать имеющуюся информацию по теме исследования в научно-популярной литературе.

2) Изучить различные виды незеркальной симметрии: поворотную симметрию, зеркально-поворотную симметрию, переносную (трансляционную) симметрию, симметрию, имеющую скользящую плоскость симметрии.

3) Рассмотреть симметрию бордюров и орнаментов.

4) Попытаться создать эскизы бордюров и орнаментов на основании полученных знаний.

Методы и методики, используемые в работе: наблюдение, эксперимент, моделирование, сравнение, обобщение, планирование, определение понятий, анализ и синтез.

Основные результаты научного исследования:

1. Получена информация по теме исследования из научно-популярной литературы.

2. Изучены различные виды незеркальной симметрии: поворотная симметрия, зеркально-поворотная симметрия, переносная (трансляционная) симметрия, симметрия, имеющая скользящую плоскость симметрии.

3. Рассмотрена симметрия бордюров и орнаментов.

4. Созданы эскизы бордюров и орнаментов на основании полученных знаний.

Наша работа является исследовательским рефератом. Мы обращались к работам по симметрии к таким авторам, как: Тарасов Л., Смирнова И., Смирнов В., Шарыгин И., а также к работе выпускницы нашей школы Морозовой Марии «Бордюры».

ВВЕДЕНИЕ

ПОСТАНОВКА ПРОБЛЕМЫ

В прошлой исследовательской работе мы рассмотрели зеркальную симметрию. Эта симметрия, которую можно непосредственно видеть. Она может быть названа геометрической или математической симметрией.

Мы убедились, что при зеркальной симметрии объект и его зазеркальный двойник при всей своей схожести могут быть разными, несовместимыми друг с другом объектами.

Симметрия встречается часто и повсеместно – как в природе, так и в человеческом творчестве. Поэтому даже неискушенный человек обычно легко усматривает симметрию в относительно простых её проявлениях.

В процессе работы над темой «Что такое зеркальная симметрия» мы выяснили, что существуют и другие виды симметрии.

Мы поняли, что симметрия буквально пронизывает весь окружающий нас мир. Принципы симметрии играют важную роль в физике и математике, химии и биологии, технике и архитектуре, поэзии и музыке. Законы природы подчиняются принципам симметрии.

Поэтому мы решили продолжить дальнейшие исследования многообразных проявлений симметрии.

В данной работе мы рассмотрим незеркальные виды симметрии.

Мы с интересом изучили работу выпускницы нашей школы, ныне студентки четвертого курса СФУ Морозовой Маши «Бордюры».

Решили рассмотреть не только симметрию бордюров, но и симметрию орнаментов.

НЕЗЕРКАЛЬНЫЕ ВИДЫ СИММЕТРИИ

ПОВОРОТНАЯ СИММЕТРИЯ

П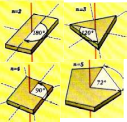 редположим, что объект совмещается сам с собой при повороте вокруг некоторой оси на угол, равный 360 градусов/n (или кратный этой величине), где n = 2, 3, 4, …. В этом случае говорят о поворотной симметрии, а указанную ось называют поворотной осью n-ого порядка (рис.2).

Р

Рисунок 1

Рисунок 2

ассмотрим пример с буквой «И» (рис.1). Она совмещается сама с собой при повороте вокруг оси на угол, равный 360 градусов/ 2, а указанную ось назовём поворотной осью 2-го порядка. На рисунке даны примеры простых объектов с поворотными осями разного порядка – от 2-го до 5-го. У трехмерного объекта может быть несколько поворотных осей (Рис.1). Например, первый объект на рисунке имеет не одну, а три поворотные оси 2-го порядка, второй объект имеет наряду с поворотной осью 3-го порядка, три поворотные оси 2-го порядка, третий объект имеет наряду с поворотной осью 4-го порядка четыре поворотные оси 2-го порядка (дополнительные поворотные оси показаны на рисунке штриховыми прямыми).

Р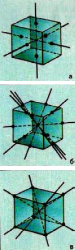

Рисунок 1

ассмотрим куб. Легко сообразить, что он имеет три поворотные оси 4-го порядка (рис.3а). При более внимательном рассмотрении обнаруживаются шесть поворотных осей 2-го порядка, проходящих через середины противоположных параллельных рёбер (рис.3б), а также четыре поворотные оси 3-го порядка, совпадающие с внутренними диагоналями куба (рис.3в). Таким образом, куб имеет всего 13 поворотных осей, среди которых встречаются оси 2-го, 3-го и 4-го порядка.

И

Рисунок 2

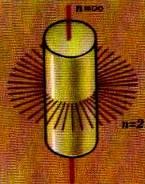
нтересна поворотная симметрия кругового цилиндра. Он имеет бесконечное число поворотных осей 2-го порядка и одну поворотную ось бесконечно высокого порядка (рис.4). Для описания симметрии конкретного объекта надо указать все поворотные оси и их порядок, а также все плоскости симметрии.

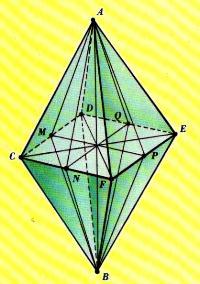
Рассмотрим, например, геометрическое тело, составленное из двух одинаковых правильных четырехугольных пирамид (приложение 1). Оно имеет одну поворотную ось 4-го порядка (ось AB), четыре поворотные оси 2-го порядка (оси CE, DF, MP, NQ), пять плоскостей симметрии (плоскости CDEF, AFBE, ACBE, AMBP, ANBQ).

ЗЕРКАЛЬНО-ПОВОРОТНАЯ СИММЕТРИЯ

В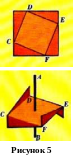 ырежем из плотной бумаги квадрат и впишем внутрь его косо другой квадрат (рис.5). Затем отогнем углы бумаги по линиям, ограничивающим внутренний квадрат (соседние углы отгибаются в противоположные стороны). В результате получим объект, показанный на рисунке. Он имеет поворотную ось 2-го порядка (ось AB) и не имеет плоскостей симметрии. Будем рассматривать наше изделие сначала сверху, а затем снизу. Мы обнаружим, что никакого различия между «верхом» и «низом» нет; в обоих случаях объект выглядит одинаково. В связи с этим возникает мысль, что поворотная симметрия 2-го порядка не исчерпывает всей симметрии данного объекта. Дополнительная симметрия, которой обладает наш объект, - это так называемая зеркально-поворотная симметрия: объект совмещается сам с собой в результате поворота на 90 градусов вокруг оси AB и последующего отражения относительно в плоскости CDEF. Ось AB называют зеркально-поворотной осью 4-го порядка. Таким образом, здесь наблюдается симметрия относительно двух последовательно выполняемых операций – поворота на 90 градусов и отражения относительно плоскости, перпендикулярной к оси поворота.

ПЕРЕНОСНАЯ (ТРАНСЛЯЦИОННАЯ) СИММЕТРИЯ

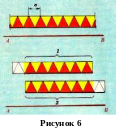Рассмотрим плоскую фигуру, изображенную на рисунке 6. При переносе (трансляции) вдоль прямой AB на расстояние a фигура совмещается сама с собой. В этом случае говорят о переносной, или трансляционной, симметрии. Прямая AB называется осью переноса, а расстояние а – элементарным переносом или периодом. Строго говоря, симметричная по отношению к переносам фигура должна быть бесконечно длинной в направлении оси переноса. Однако понятие переносной симметрии применяют и в случае фигур конечных размеров, имея в виду наблюдаемое при переносе частичное совмещение фигуры. Из рисунка видно, что при переносе конечной фигуры на расстояние а вдоль прямой AB наблюдается совмещение участка 1 и участка 2.

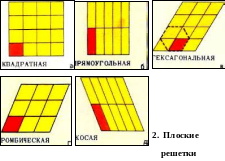
С переносной симметрией связано важное понятие двухмерной периодической структуры – плоской решетки. Плоская решетка может быть образована в результате пересечения двух семейств параллельных, равноотстоящих друг от друга прямых (рис.7). Точки пересечения прямых называются узлами решетки. Чтобы задать решетку, достаточно задать ее элементарную ячейку и затем переносить эту ячейку параллельно самой себе вдоль прямой AB на расстояния, кратные а, либо вдоль прямой AC на расстояния кратные b. Заметим, что элементарную ячейку данной решетки можно выбрать разными способами. Так, можно выбрать в качестве элементарной ячейку, которая на рисунке закрашена красным цветом. Однако можно было бы воспользоваться и любой из заштрихованных на рисунке ячеек.

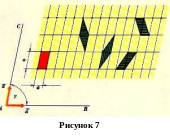Переносная симметрия плоской решетки полностью определяется совокупностью двух векторов (векторов a и b на рисунке).

Различают пять типов плоских решеток; они показаны в приложении 2: а) a = b, y = 90 градусов (квадратная решетка); б) a не = b, y = 90 градусов (прямоугольная решетка); в) a=b, y=60 градусов (гексагональная решетка); г) a=b, y не = 90 градусов, y не = 60 градусов (ромбическая решетка); д) а не = b, y не = 90 градусов (косая решетка).

С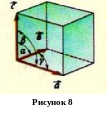 переносной симметрией в трехмерном пространстве связано понятие трехмерной периодической структуры – пространственной решетки. Такая решетка может рассматриваться как результат пересечения трех семейств параллельных плоскостей. Переносная симметрия трехмерной решетки определяется совокупностью трех векторов, задающих элементарную ячейку решетки. На рисунке 8 показана ячейка решетки, задаваемая векторами a, b, c. В простейшем случае длины всех ребер ячейки равны между собой, а углы между ребрами составляют 90 градусов. В этом случае говорят о кубической решетке.

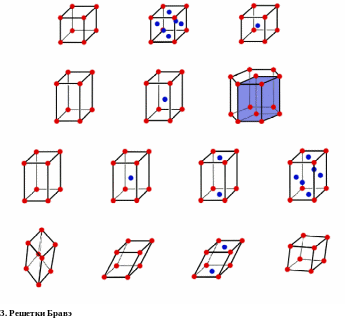
Всего же существует 14 типов пространственных решеток, различающихся по типу переносной симметрии. Иначе говоря, существует 14 типов решеток Браве (Браве – французский кристаллограф XIX века) (Приложение 3).

Скользящая плоскость (ось) симметрии.

Ранее было показано, что с последовательно выполняемыми операциями поворота и отражения может быть связан новый тип симметрии – зеркально-поворотная симметрия. Комбинирование поворотов или отражений с переносами также может выявить новые типы с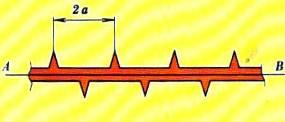 имметрии. В качестве примера отметим симметрию, отвечающую наличию так называемой скользящей плоскости симметрии (точнее, скользящей оси симметрии, так как р

Рисунок 9

ассматривается плоская фигура). На рисунке 9 изображена фигура, обладающая переносной симметрией вдоль оси AB c периодом 2а. Нетрудно видеть, что здесь имеет место еще один тип симметрии – симметрия относительно переноса вдоль оси AB с периодом а и последующего отражения относительно оси AB. Ось AB называется скользящей осью симметрии с периодом а.

Бордюры и орнаменты

Математик, так же как художник или поэт, создает узоры.

Г. Харди

Бордюры

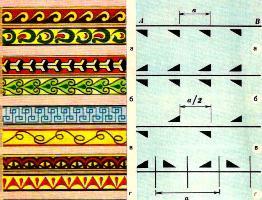
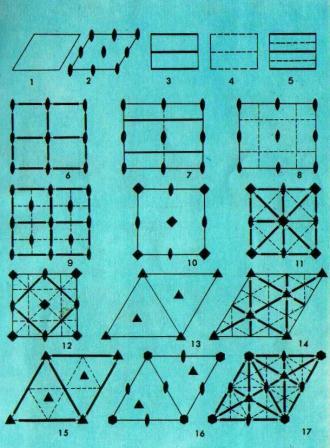
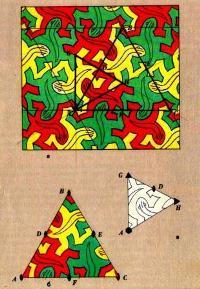
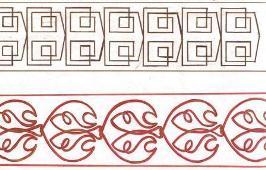
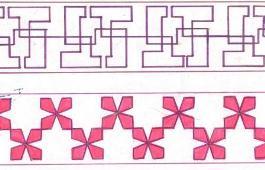
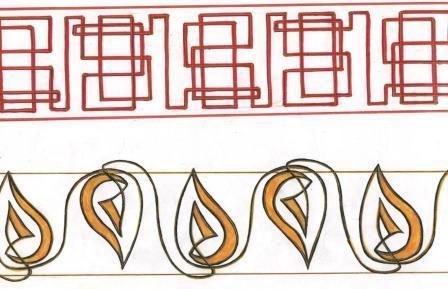
Периодически повторяющийся рисунок на длинной ленте называют бордюром. На практике бордюры встречаются в различных видах. Это может быть настенная роспись, украшающая стены зданий, галереи, лестничные переходы. Это моет быть чугунное литье, используемое в оградах парков, решетках мостов и набережных. Это могут быть гипсовые барельефы или керамика. В приложении 4 представлены 14 бордюров, разбитых на 7 пар. В каждую пару входят бордюры, одинаковые по типу симметрии. Всего существует 7 типов симметрии бордюров. Любой бордюр обладает переносной симметрией вдоль своей оси. В простейшем случае симметрия бордюра полностью исчерпывается переносной симметрией. Схематически бордюр этого типа показан на рисунке (А), где треугольник условно обозначает повторяющийся несимметричный элемент бордюра. Бордюры, показанные на рисунке (Б), обладают наряду с переносной также зеркальной симметрией: они зеркально симметричны относительно прямой, делящей ленту бордюра пополам в продольном направлении. Здесь ось переноса является также осью симметрии. У бордюров, показанных на рисунках (В), ось переноса является осью скользящего отражения.

Бордюры, показанные на рисунке (Г), имеют поперечные оси симметрии. Эти оси изображены на рисунке (Г) в виде отрезков прямых, перпендикулярных к оси переноса. На рисунке (Д) показаны бордюры, имеющие поворотные оси 2-го порядка, перпендикулярные к плоскости бордюра. Точки пересечения этих осей с плоскостью бордюра отмечены на рисунке (Д) закрашенными чечевицами. На комбинировании оси скользящего отражения с поворотными осями 2-го порядка, перпендикулярными к плоскости бордюра, основаны бордюры, изображенные на рисунке (Е); в результате такого комбинирования возникают поперечные оси симметрии. Наконец, на рисунках (Ж) представлены бордюры, основанные на комбинировании зеркальных отражений. Такие бордюры имеют наряду с продольной также поперечные оси симметрии; как следствие возникают поворотные оси 2-го порядка.

ОРНАМЕНТЫ

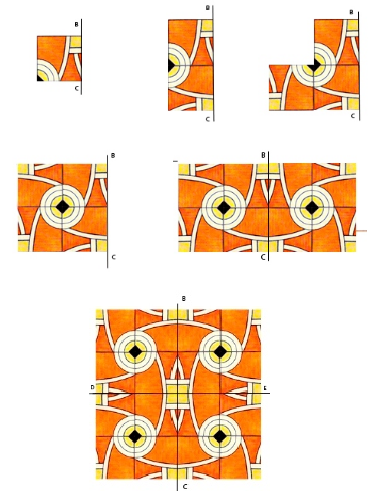
Трудно найти человека, не любовавшегося орнаментами- этими удивительными рисунками, часто встречающими в декоративном художественном творчестве. В них можно обнаружить затейливое сочетание переносной, зеркальной и поворотной симметрий. За примером орнамента не надо далеко ходить - взгляните на рисунок обоев, которыми оклеены стены вашей комнаты. Некоторые образцы орнаментов показаны в приложениях 5-7. Среди них два созданы известным голландским художником Эшером – орнаменты «Летящие птицы» (прил.5) и «Ящерицы» (прил.7).

В основе любого орнамента лежит одна из пяти рассмотренных в главе 2 плоских решёток. Тип плоской решётки определяет характер переносной симметрии данного орнамента. Орнамент «Летящие птицы» основан на косой решётке, характерный египетский орнамент основан на квадратной решётке, а орнамент «Ящерицы» - на гексагональной решётке.

В простейшем случае орнамент характеризуется только переносной симметрией. Таков, например, орнамент «Летящие птицы». Чтобы построить этот орнамент, надо выбрать соответствующую косую решётку, «заполнить» элементарную ячейку решётки определённым рисунком и затем многократно повторить этот рисунок за счет переносов ячейки без изменеия её ориентации. В приложении 8 элементарная ячейка орнамента заштрихована. Заметим, что площадь ячейки равна сумме площадей, занимаемых изображениями птиц разного цвета.

В приложении 9 рассмотрена симметрия египетского орнамента.

Переносная симметрия орнамента определяется квадратной решёткой, элементарная ячейка которой выделена на рисунке а. Эта ячейка имеет поворотные оси 2- го порядка, обычные и скользящие оси симметрии. На рисунке б сплошными прямыми показаны обычные оси симметрии, а штриховыми – скользящие. Точки пересечения поворотных осей 2- го порядка с плоскостью орнамента обозначены закрашенными чечевицами.

В отличие от орнамента «Летящие птицы» данный орнамент обладает более высокой симметрией, о чём свидетельствует наличие поворотных осей, а также обычных и скользящих осей зеркальной симметрии.

Симметрия египетского орнамента будет ещё более высокой, если упростить его раскраску- вместо красного и синего цветов использовать один цвет, например, красный. В этом случае дополнительно появляются поворотные оси 4- го порядка и, кроме того, увеличивается число скользящих осей симметрии.

Симметрия такого орнамента показана в приложении 9в, где закрашенными квадратиками обозначены точки пересечения поворотных осей 4- го порядка с плоскостью орнамента.

Рисунки б и в в приложении 9 содержат полную информацию о характере симметрии соответствующих орнаментов. Если на этих рисунках убрать узор, сохранив лишь обозначения обычных и скользящих осей симметрии, а также точек пересечения поворотных осей с плоскостью орнамента, то получается схематическое изображение двух разных типов симметрии орнаментов. Всего существует 17 типов симметрии плоских орнаментов. Они приведены в приложении 10. Здесь толстые прямые линии изображают обычные оси симметрии, а штриховые – скользящие. Для обозначения точек пересечения поворотных осей с плоскостью орнамента используются чечевицы (оси 2 –го порядка), треугольники (3-го порядка), квадратики (4 –го), шестиугольники (6-го). Орнамент, показанный на рисунке б, представлен в приложении 10 позицией 9, а орнамент, показанный на рисунке в, - позицией 12; орнаменту «Летящие птицы» отвечает позиция 1.

В принципе любой орнамент можно построить так, как строился орнамент «Летящие птицы»: посредством параллельных переносов заполненной определённым рисунком элементарной ячейки. Такой способ построения орнамента является единственным в том случае, когда орнамент не обладает ни поворотной, ни зеркальной симметрией. В остальных случаях возможны иные способы построения орнамента; при этом в качестве исходного изображения (как говорят, основного мотива) используют не всю элементарную ячейку орнамента, а лишь часть её.

Обратимся к египетскому орнаменту, показанному в приложении 6.

В качестве основного мотива этого орнамента может быть выбрано изображение в пределах прямоугольника, однократно заштрихованного в приложении 9 а (площадь прямоугольника составляет одну восьмую площади элементарной ячейки орнамента). Этот основной мотив показан отдельно в приложении 11 а.

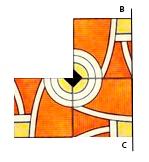
Для построения орнамента воспользуемся осями симметрии ВС и DE, показанными в приложениях 9 и 11, а также поворотной осью 2-го порядка, проходящей через точку А. Зафиксируем точку F и оси BC и DE на плоскости рисунка и, используя основной мотив (рис. а), будем выполнять отражения относительно ВС и DE и повороты на 180 вокруг точки А в любой последовательности и сколь угодно долго. Поворот вокруг точки А превращает рисунок а в рисунок б (прил.9); последующее отражение относительно ВС приводит к рисунку в. Затем производим отражение относительно DE (получаем рисунок г), новый поворот на 180 вокруг А (получаем рисунок д), новое отражение относительно ВС и т.д. По мере выполнения поворотов и отражений орнамент как бы расцветает на наших глазах, всё более и более заполняя площадь рисунка.

Рассмотрим египетский орнамент с упрощённой раскраской (прил. 9 в). Теперь в качестве основного мотива можно выбрать изображение в пределах квадрата, заштрихованного в клеточку на рисунке а. Самостоятельно выполняем построение орнамента. Для этого воспользуемся поворотной осью 4- го порядка и осью симметрии ВС (прил.12).

В приложении 13 показаны бордюры из математической копилки, созданной Машей Морозовой.

ВЫВОДЫ

1. Мы рассмотрели незеркальную симметрию. Эта симметрия положений, форм, структур. Её можно непосредственно видеть. Как и зеркальная симметрия, она может быть названа геометрической.

2. Мы выяснили, что существует несколько видов незеркальной симметрии.

3. Мы поняли, что она связана с упорядоченностью и уравновешенностью, пропорциональностью и соразмерностью частей, простотой и гармонией (а иногда с однообразием), когда познакомились с удивительными рисунками – орнаментами и бордюрами и попытались создать свои эскизы.

Итак, мы познакомились с геометрической симметрией. Но симметрия лежит в самой основе естественнонаучной картины мира, в физических явлениях и законах природы; и её можно назвать физической симметрией.

Хотелось бы в дальнейшем рассмотреть симметрию в природе.

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ

1) Азевич А.И. 20 уроков гармонии - М.: 1998 (Библиотека журнала «Математика в школе». Выпуск 7).

2) Земляков А. Орнаменты - Квант.- 1977- № 3.

3) Лэнгдон Н., Снейп Ч. С математикой в путь - М.: Педагогика, 1987.

4) Смирнова И., Смирнов В. Паркеты (библиотечка газеты «Первое сентября») - М.: Чистые пруды, 2009.

5) Таболников С. Вариации на тему Эшера - Квант.- 1990.- № 12.

7) Тарасов Л. Этот удивительно симметричный мир - М.: Просвещение, 1982.

8) Федоров Е. С. Симметрия на плоскости – СПб. , 1981.

9) Цукарь А. Геометрические преобразования и паркеты - Математика. Приложение к газете « Первое сентября». -1999. - № 47.

10) Цукарь А. Бордюры - Математика. Приложения к газете «Первое сентября». - 1998 - № 48.

11) Шарыгин И. Ф., Ерганжиева Л. Н. « Наглядная геометрия. 5 - 6 классы» - М.: Дрофа, 2007.

11

ПРИЛОЖЕНИЯ

5. Морис Эшер. «Летящие птицы»

6. Египетский орнамент

4. Типы бордюров

7. Морис Эшер «Ящерицы»

8. Морис Эшер «Летящие птицы» . Переносная симметрия

10. 17 типов симметрии плоских орнаментов

9. Симметрия Египетского орнамента

11. Построение египетского орнамента

12. Самостоятельное построение орнамента.

13. Симметрия орнамента «Ящерицы»

14. Из математической копилки

Морозовой Маши

КАЛЕНДАРНЫЙ ПЛАН ИССЛЕДОВАТЕЛЬСКОЙ РАБОТЫ

Дата записи	Вид деятельности	Результат	Примечания
06.06.2012 – 14.06.02012	Выбор темы.	Определились с темой «От зеркальной симметрии к бордюрам и орнаментам».	Составили план работы: Изучение научно – популярной литературы и Интернет – источников по теме исследования. Нахождение различных типов незеркальной симметрии. Оформление работы.
14.06.2012	Определение целей и задач исследования.	Цель работы: Изучение незеркальных видов симметрии.
14.06.2012 – 20.06.2012	Подбор информации по теме исследования в научно – популярной литературе и Интернет ресурсах.	Найдена информация статей по теме «Что такое незеркальные виды симметрии?».
20.06.2012 – 06.10.2012	Подбор информации по теме исследования в научно – популярной литературе и Интернет – ресурсах. Обработка полученной информации.	Написаны вопросы: Виды незеркальной симметрии: А) Поворотная симметрия. Б) Зеркально – поворотная симметрия.	Обобщение полученных данных.
06.10.2012 – 03.11.2012	Обработка информации.	Написана часть работы: Виды незеркальной симметрии: В) Переносная (трансляционная) симметрия Г) Скользящая плоскость (ось) симметрии.	Обобщение полученных данных.
	Обработка полученной информации	Написано: « Бордюры », « Орнаменты »	Обобщение полученных данных
01.12.12. – 22.12.12.	Обработка полученной информации	Выполнение египетского орнамента по основному мотиву	Обобщение полученных данных
22.12.12. – 19.01.12.	Обработка информации	Написаны заключения, выводы	Обобщение полученных данных
19.01.12 – 25.01.12	Оформление работы, представление её на конкурс	Оформление работы в соответствии с требованиями
19.01.12- 25.01.12	Оформление презентации работы и доклада	Оформлен доклад	Тема: « От зеркальной симметрии к бордюрам и орнаментам »
19.01.12- 25.01.12	Оформление презентации к докладу	Оформление презентации в соответствии с требованиями	Тема: « От зеркальной симметрии к бордюрам и орнаментам ». На слайдах представлены: цель работы, задачи, выводы.

Районная научно-практическая конференция «Новое поколение Курагинского района» для 8-11 классов
Заявитель (ШНОУ)	МБОУ Курагинская средняя общеобразовательная школа №3
Полное название темы работы	От зеркальной симметрии к бордюрам и орнаментам
Название секции конференции	Математика
Тип работы	Исследовательский реферат
Возрастная номинация	8-11 класс
Фамилия имя отчество (полностью) автора, дата рождения	Бордюгова Ольга Сергеевна, 10.06.1998 Евсеева Маргарита Эдуардовна, 14.08.1998
Домашний адрес автора	662910 поселок Курагино Красноярского края, ул. Степная,18 662910 поселок Курагино Красноярского края, ул. Советская, 82
Место учебы:	МБОУ Курагинская средняя общеобразовательная школа №3
Класс	8 Б класс
Место выполнения работы	Школьное научное объединение
Руководитель	Юдина Ольга Ивановна, учитель математики МБОУ КСОШ №3
Научный руководитель
Ответственный за корректуру текста работы	Брух Светлана Александровна, учитель русского языка и литературы МБОУ КСОШ №3
Е-mail (обязательно) Контактный телефон	Контактный телефон авторов: 2-21-61; 2-34-72 E-mail авторов: evseeva-09@mail.ru; olga_bordyugova@mail.ru Контактный телефон руководителя: 2-51-67