
ФИЛИАЛ «САМАРСКИЙ МЕДИКО-СОЦИАЛЬНЫЙ КОЛЛЕДЖ» ГБПОУ «САМАРСКИЙ МЕДИЦИНСКИЙ КОЛЛЕДЖ им. Н. ЛЯПИНОЙ»
Открытое занятие
Тема 1.7.: «Начала математического анализа»
Раздел темы 1.7.4. «Применение производной к исследованию функций на экстремумы»
ДИСЦИПЛИНА: ОУД.03 «МАТЕМАТИКА: АЛГЕБРА И
НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА; ГЕОМЕТРИЯ»
специальность: 33.02.01 Фармация
Подготовила:
Котова Ю.Ю.,
преподаватель
математики
2016г.

Цели занятия:
- обобщить знания о производной функции и её применении для исследования функции;
- отработать алгоритм применения схемы исследования функции на экстремумы.

«Знания имей отличные, исследуй функции различные!»

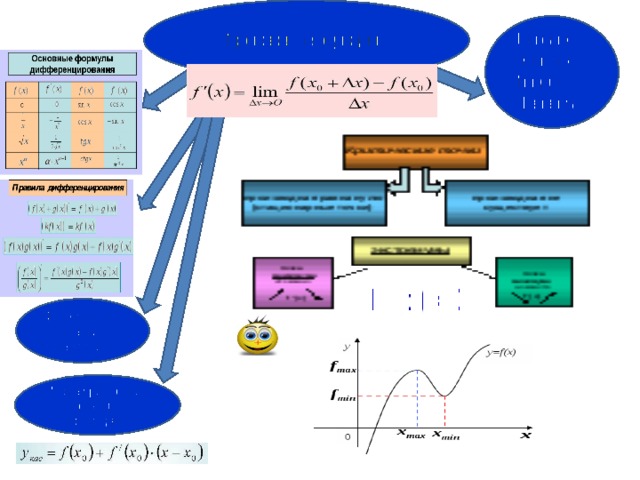
Найти производную функции
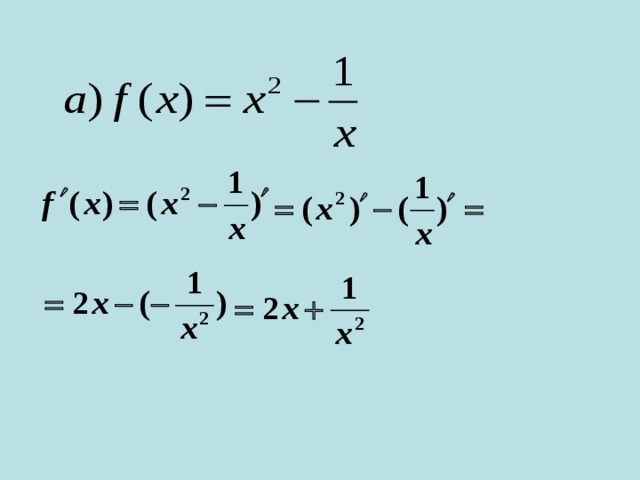
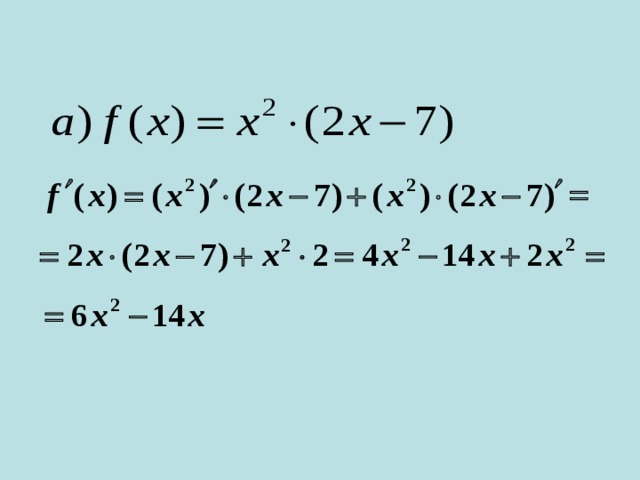
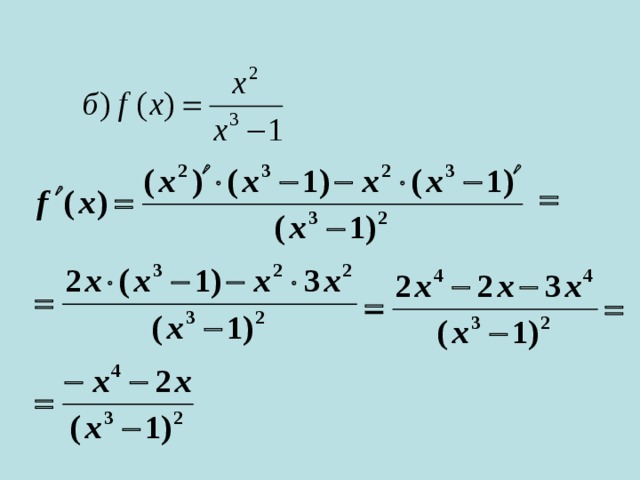

Проверка домашнего задания:
( 3 √(x 2 -cosx) 2 )′= (2x+sinx) / 3 √(x 2 -cosx)
(ln 7 (x 2 -3x+1))′=(14x-21) ln 6 (x 2 -3x+1) /
(x 2 -3x+1)

(проверка знания
правил и формул дифференцирования)
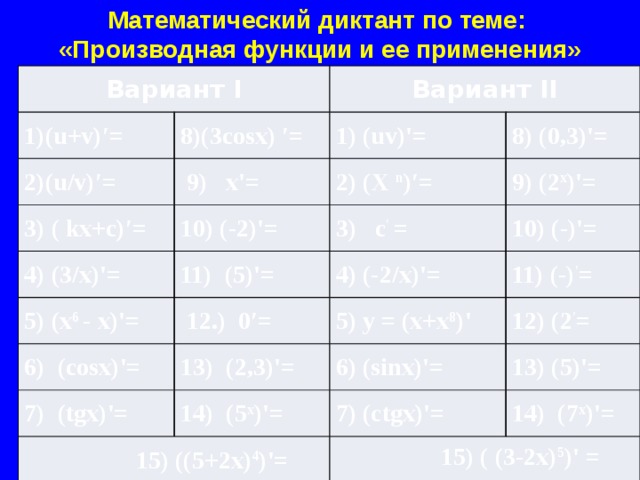
Математический диктант по теме:
«Производная функции и ее применения»
Вариант I
1)(u+v)′=
Вариант II
8)(3cosx) ′=
2)(u/v)′=
1) (uv)'=
9) х'=
3) ( kx+c)′=
4) (3/x)'=
8) (0,3)'=
2) (Х n )′=
10) (-2)'=
5) (x 6 - x)'=
11) (5)'=
3) c ′ =
9) (2 х )'=
10) (-)'=
4) (-2/x)'=
12.) 0′=
6) (сosx)'=
11) (-) ′ =
5) y = (x+x 8 )'
7) (tgx)'=
13) (2,3)'=
12) (2 ′ =
6) (sinx)'=
14) (5 x )'=
15) ((5+2x) 4 )'=
13) (5)'=
7) (сtgx)'=
14) (7 х )'=
15) ( (3-2x) 5 )' =
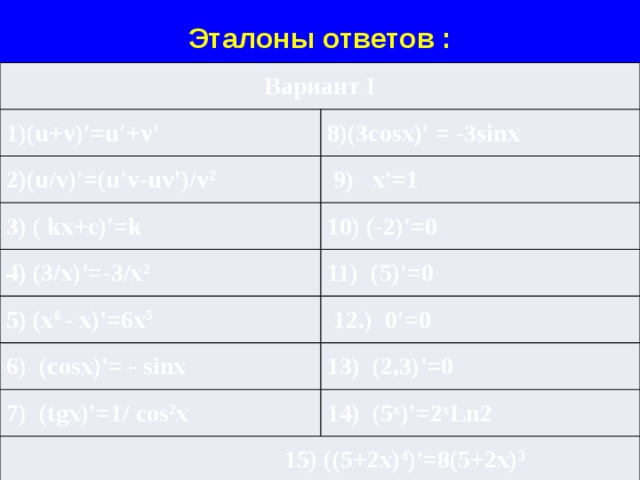
Эталоны ответов :
Вариант I
1)(u+v)′=u′+v′
8)(3cosx)′ = -3sinx
2)(u/v)′=(u′v-uv′)/v 2
9) х'=1
3) ( kx+c)′=k
4) (3/x)'=-3/x 2
10) (-2)'=0
11) (5)'=0
5) (x 6 - x)'=6x 5
12.) 0′=0
6) (сosx)'= - sinx
13) (2,3)'=0
7) (tgx)'= 1/ сos 2 х
14) (5 x )'= 2 x Ln2
15) ((5+2x) 4 )'=8(5+2x) 3
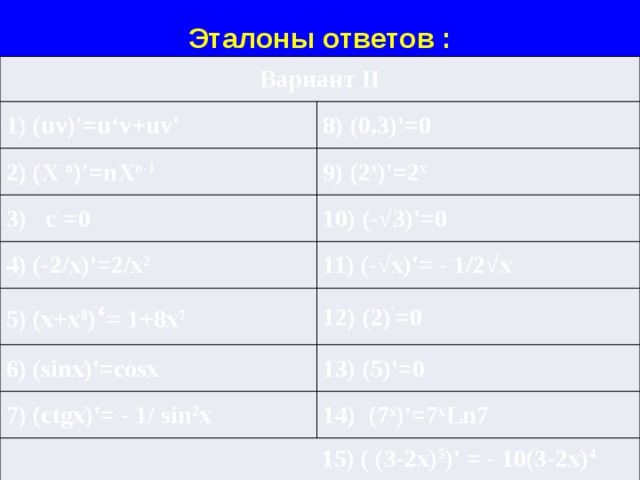
Эталоны ответов :
Вариант II
1) (uv)'=u‘v+uv'
8) (0,3)'=0
2) (Х n )′=nX n-1
9) (2 х )'=2 х
3) c ′ =0
10) (-√3)'=0
4) (-2/x)'=2/x 2
5) (x+x 8 ) ‘ = 1+8x 7
11) (-√x)'= - 1/2√x
12) (2) ′ =0
6) (sinx)'=cosx
13) (5)'=0
7) (сtgx)'= - 1/ sin 2 x
14) (7 х )'=7 х Ln7
15) ( (3-2x) 5 )' = - 10(3-2x) 4

“ Эстафета”
Математическая эстафета
(14х 6 ) ′
(5) ′
(7 х ln 7) ′
(10(3-2х) 4 ) ′
(12х 3 ) ′
(3) ′
(5 х ln 8) ′
(5-7х) ′
Спеши! Успевай!
Про товарища
не забывай!!!

Эталоны ответов 1 команды:

Эталоны ответов 2 команды:

Точка движется прямолинейно по закону
Вычислите скорость и ускорение точки при t =1.
Решение: v (t)=S ′ (t) = 6t 2 +t v (1)=6+1=7(м/с)
a(t)=( 6t 2 +t) ′ =12t+1
a(1)=12(м/с 2 )
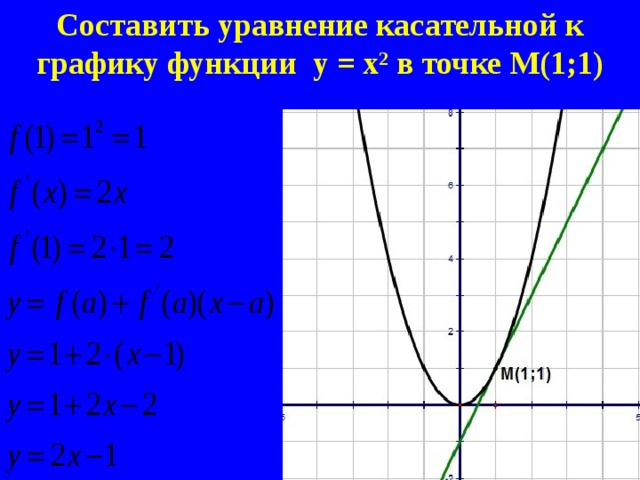
Составить уравнение касательной к графику функции у = х 2 в точке М(1;1)
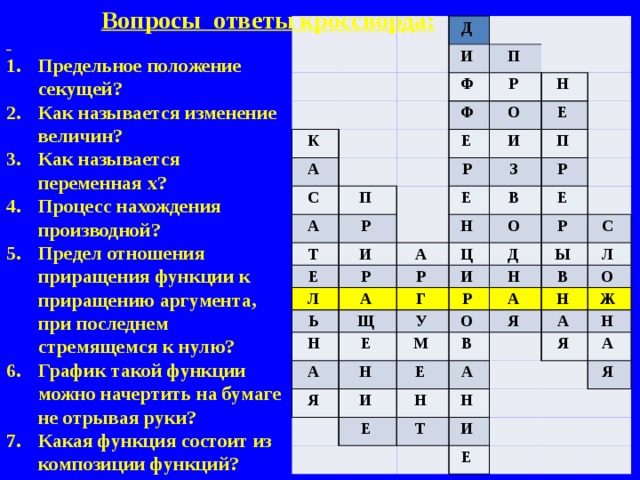
Вопросы ответы кроссворда:
Д
К
И
Ф
П
А
С
Р
Ф
Н
О
Е
А
П
Т
Р
Е
И
Р
Е
П
И
Е
З
Р
Р
В
Л
Н
А
А
Р
Ц
Ь
О
Е
Н
Д
И
Р
Щ
Г
Е
А
Н
Ы
С
Р
У
Л
Я
Н
В
А
О
М
О
И
Я
В
Н
Е
Ж
Е
Н
А
А
Н
Н
Я
Т
А
И
Я
Е
- Предельное положение секущей?
- Как называется изменение величин?
- Как называется переменная х?
- Процесс нахождения производной?
- Предел отношения приращения функции к приращению аргумента, при последнем стремящемся к нулю?
- График такой функции можно начертить на бумаге не отрывая руки?
- Какая функция состоит из композиции функций?
Дифференциальное исчисление- это описание окружающего нас мира, выполненное на математическом языке. Производная помогает нам успешно решать не только математические задачи, но и задачи практического характера в разных областях науки, техники и жизни.

Лагранж - это имя ученого, который ввёл термин « производная » , ему же мы обязаны и современным обозначением производной (с помощью штриха). Термин « вторая производная » и обозначение (два штриха) также ввёл он. В 19 лет он стал профессором в Артиллерийской школе Турина.

Дифференциальное исчисление — математический язык классической физики.
Исаак Ньютон (1643-1727) один из создателей дифференциального исчисления. Главный его труд- «Математические начала натуральной философии».-оказал колоссальное влияние на развитие естествознания, стал поворотным пунктом в истории естествознания. Ньютон ввёл понятие производной, изучая законы механики, тем самым раскрыл её механический смысл.
Недаром английский писатель А Поуг сказал: «Был этот мир глубокой тьмой окутан. Да будет свет! И вот явился Ньютон!»

Когда дело доходило до конкурентов на интеллектуальном поприще, Ньютон мог быть ревнивым и мстительным. К примеру, он враждовал с немецким математиком и философом Готфридом Лейбницем. Мужчины вели ожесточенную борьбу за то, кто из них изобрел дифференциальное исчисление. Ньютон разработал систему в 1660-х годах, но не опубликовал. Лейбниц сформулировал собственную систему и опубликовал ее десять лет спустя. Чтобы решить этот спор, был собран комитет при Королевском научном сообществе, куда обратился Лейбниц.
Однако Ньютон служил президентом этой организации, поэтому ему удалось собрать комитет со своими сторонниками. В результате его публично признали автором этого изобретения. Тем не менее сегодня используется именно система Лейбница.

В 1705 году Эдмон Галлей предсказал, что комета, которую наблюдали в 1531, 1607 и 1682 годах, должна возвратиться в 1758 году
Используя методы дифференциального исчисления английский астроном, математик Эдмон Галлей ещё в XVII веке предсказал возвращение кометы Галлея.
(что, увы, было уже после его смерти). Комета действительно возвратилась, как было рассчитано, и позже была названа в его честь. Комета Галлея вернется во внутреннюю Солнечную систему в следующий раз в 2061 году.
Различные математические исследования
встречаются и в
работах
Рене Декарта .
Большой вклад в изучение дифференциального исчисления внес Леонард Эйлер .

« Все, что до этого было в науках: темно, сомнительно и недостоверно, математика сделала ясным, верным и очевидным …»
« Математику уже затем учить надо, что она
ум в порядок приводит » М.В. Ломоносов
Применение производной к исследованию функций

Изучение нового материала:
- подумаем, что об этом мы уже знаем или
предполагаем;
- вдумчиво прочитаем текст используя Инсерт;
- снова вернёмся к вопросам, рассмотренным
в начале знакомства с новым материалом,
обсудим - правы ли мы были, а если нет, то
в чём ошиблись;
- закрепим полученные знания на практике;
- подведём итоги урока
 х 1 , так и f(х 2 ) f(х 1 )? 3. Если функция, определённая на интервале, в каждой точке имеет положительную производную, то данная функция возрастает на этом интервале? 4. Для убывания дифференцируемой на интервале функции необходимо, чтобы её производная во всех точках интервала принимала отрицательные значения? 5. Если функция возрастает в интервале, то угловой коэффициент касательных к графику этой функции в любой точке интервала будет положительным? 6. Можно ли с помощью производной функции найти максимальное или минимальное значение функции. " width="640"
х 1 , так и f(х 2 ) f(х 1 )? 3. Если функция, определённая на интервале, в каждой точке имеет положительную производную, то данная функция возрастает на этом интервале? 4. Для убывания дифференцируемой на интервале функции необходимо, чтобы её производная во всех точках интервала принимала отрицательные значения? 5. Если функция возрастает в интервале, то угловой коэффициент касательных к графику этой функции в любой точке интервала будет положительным? 6. Можно ли с помощью производной функции найти максимальное или минимальное значение функции. " width="640"
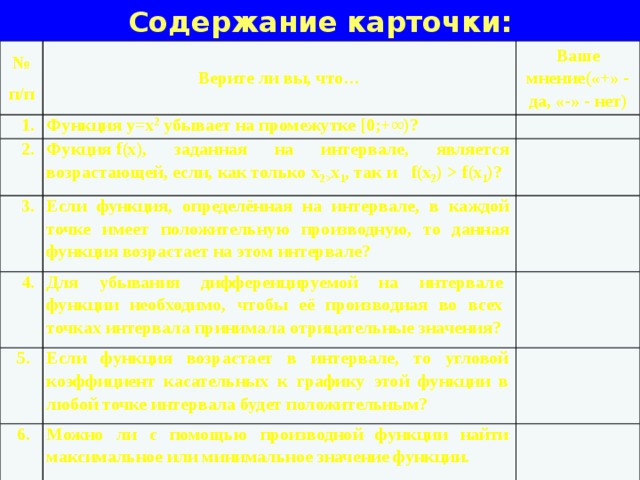
Содержание карточки:
№
Верите ли вы, что…
1.
п/п
Ваше мнение(«+» - да, «-» - нет)
Функция у=х 2 убывает на промежутке [0;+∞)?
2.
Фукция f(х), заданная на интервале, является возрастающей, если, как только х 2 х 1 , так и f(х 2 ) f(х 1 )?
3.
Если функция, определённая на интервале, в каждой точке имеет положительную производную, то данная функция возрастает на этом интервале?
4.
Для убывания дифференцируемой на интервале функции необходимо, чтобы её производная во всех точках интервала принимала отрицательные значения?
5.
Если функция возрастает в интервале, то угловой коэффициент касательных к графику этой функции в любой точке интервала будет положительным?
6.
Можно ли с помощью производной функции найти максимальное или минимальное значение функции.

Инсерт
- Знак «галочка» (V) – отметьте в тексте уже известную вам информацию;
- Знак «галочка» (V) – отметьте в тексте уже известную вам информацию;
- Знак «плюс» (+) – отметьте новую информацию;
- Знак «плюс» (+) – отметьте новую информацию;
- Знак «минус» (-) – отмечается то, что идет вразрез с имеющимися у вас представлениями, то, о чем вы думали иначе;
- Знак «минус» (-) – отмечается то, что идет вразрез с имеющимися у вас представлениями, то, о чем вы думали иначе;
- Знак «вопрос» (?) – отмечается то, что осталось непонятным и требует дополнительного изучения и понимания, то, о чем вы бы хотели узнать подробнее.
- Знак «вопрос» (?) – отмечается то, что осталось непонятным и требует дополнительного изучения и понимания, то, о чем вы бы хотели узнать подробнее.
 0. Теорема 2. Функция f (x) убывает на интервале (a; b) тогда и только тогда, когда для любого х из (a; b) f ′ (х) Правило нахождения интервалов монотонности. Находим производную f ′ (х), Находим точки в которых f ′ (х)=0 или не существует. Эти точки называются критическими для функции f . Критические точки разбивают область определения на интервалы, на каждом из которых производная f ′ (х) сохраняет свой знак. Эти интервалы будут интервалами монотонности. Определяем знак f ′ (х) на каждом из найденных интервалов. Если f ′ (х)0 на интервале, то на нем функция возрастает, если f ′ (х) " width="640"
0. Теорема 2. Функция f (x) убывает на интервале (a; b) тогда и только тогда, когда для любого х из (a; b) f ′ (х) Правило нахождения интервалов монотонности. Находим производную f ′ (х), Находим точки в которых f ′ (х)=0 или не существует. Эти точки называются критическими для функции f . Критические точки разбивают область определения на интервалы, на каждом из которых производная f ′ (х) сохраняет свой знак. Эти интервалы будут интервалами монотонности. Определяем знак f ′ (х) на каждом из найденных интервалов. Если f ′ (х)0 на интервале, то на нем функция возрастает, если f ′ (х) " width="640"
Текст лекции:
1часть лекции
Функция монотонна на неком промежутке, когда она возрастает или убывает на избранном интервале .
Из задач на нахождение касательной видно, что функция возрастает, если её угловой коэффициент положителен и убывает, если он отрицателен. Но угловой коэффициент касательной – это производная функции в точке касания, следовательно справедливы теоремы.
Теорема 1 . Функция f возрастает на интервале (а; в) тогда и только тогда, когда для любого х из (а;в) f ′ (х)0.
Теорема 2. Функция f (x) убывает на интервале (a; b) тогда и только тогда, когда для любого х из (a; b) f ′ (х)
Правило нахождения интервалов монотонности.
- Находим производную f ′ (х),
- Находим точки в которых f ′ (х)=0 или не существует. Эти точки называются критическими для функции f .
- Критические точки разбивают область определения на интервалы, на каждом из которых производная f ′ (х) сохраняет свой знак. Эти интервалы будут интервалами монотонности.
- Определяем знак f ′ (х) на каждом из найденных интервалов.
- Если f ′ (х)0 на интервале, то на нем функция возрастает, если f ′ (х)
y
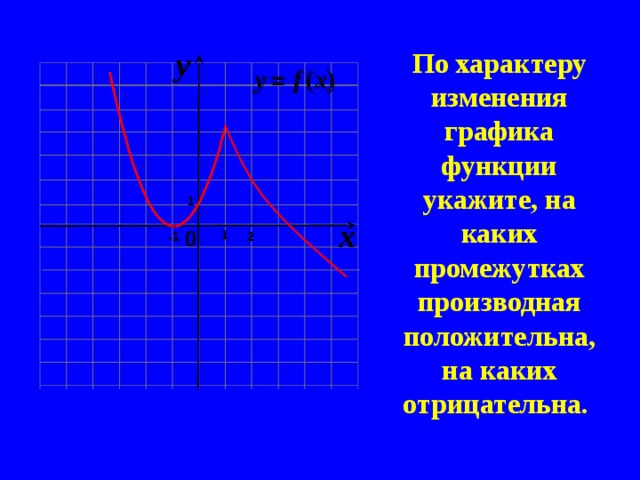
По характеру изменения графика функции укажите, на каких промежутках производная положительна, на каких отрицательна.
1
x
0
1
-1
2

2 часть лекции
Исследование на экстремумы.
Определение. Точка х 0 называется точкой максимума , если в ней возрастание сменяется убыванием. Точка х 0 называется точкой минимума, если в ней убывание сменяется возрастанием.
Теорема 3.
Если точка х 0 является точкой максимума или минимума функции у = f (х), то f ′ (х) = 0 (или она не существует в этой точке).
Теорема 4. Если производная f ′ (х) при переходе через точку х 0 меняет знак с плюса на минус, то х 0 является точкой максимума. Если производная f ′ (х) при переходе через точку х 0 меняет знак с минуса на плюс, то точка х 0 является точкой минимума.
Точки минимума и максимума называются точками экстремумов.

Достаточные условия экстремума.
Пусть функция у = f(х) непрерывна на некотором промежутке и имеет внутри промежутка точку экстремума х = х 0 , тогда:
х 0
а) х = х 0 - точка минимума, если в ней данная функция переходит с убывания на возрастание, а производная данной функции переходит с «-» на «+».
f ′ (х)
+
–
f (х)
х
х min
Экстремум- минимум
х 0
+
б) х = х 0 - точка максимума, если в ней данная функция переходит с возрастания на убывание, а производная данной функции переходит с «+» на «-».
f ′ (х)
–
х
f (х)
х max
Экстремум - максимум
f ′ (х)
+
х 0
+
х
f (х)
в) в точке х = х 0 экстремума нет, если по обе стороны от этой точки функция не меняет монотонность, а производная имеет одинаковый знак.
Экстремума нет, точка перегиба
f ′ (х)
–
–
х 0
х
f (х)
Экстремума нет, точка перегиба
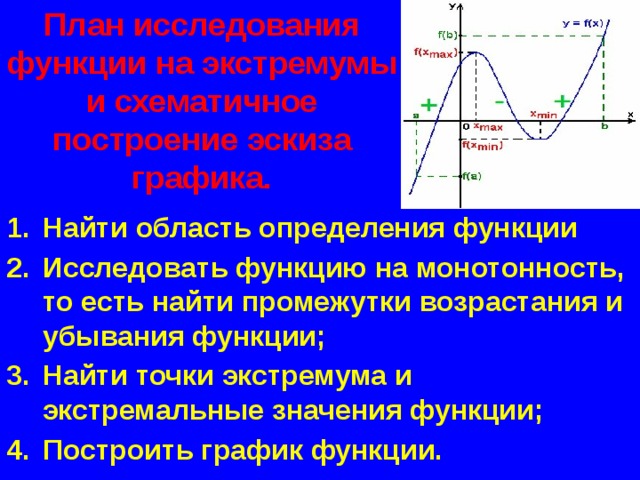
План исследования функции на экстремумы и схематичное построение эскиза графика.
- Найти область определения функции
- Исследовать функцию на монотонность, то есть найти промежутки возрастания и убывания функции;
- Найти точки экстремума и экстремальные значения функции;
- Построить график функции.

3 часть лекции
Правило нахождения точек экстремумов.
- Найдите критические точки.
- Исследуйте знак производной f ′ (х) в окрестности каждой точки
на монотонность.
Пример. Найдите экстремумы функции f (х) = 0,25х 4 - 2х 2 +5
Решение: 1) находим первую производную:
f ′ (х) = x 3 +4x
Приравниваем производную к нулю:
x 3 +4x=0, решаем данное уравнение и находим критические
точки первого рода:
х(х 2 -4)=0, х 1 =0, х 2 =4 , получаем:
х 1 =0, х 2 =2, х = -2 – критические точки 1 рода
Выставляем данные критические точки на координатную прямую и проверяем знаки в интервалах, определяем, как ведет себя функция, где она возрастает, где убывает в зависимости от знака её производной
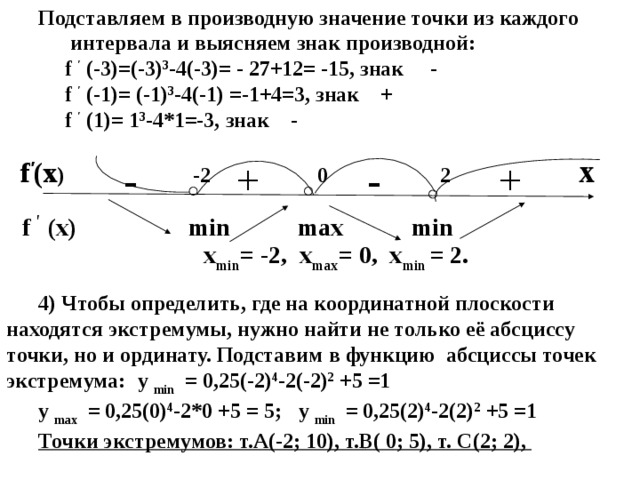
Подставляем в производную значение точки из каждого
интервала и выясняем знак производной:
f ′ (-3)=(-3) 3 -4(-3)= - 27+12= -15, знак -
f ′ (-1)= (-1) 3 -4(-1) =-1+4=3, знак +
f ′ (1)= 1 3 -4*1=-3, знак -
- + - +
f ′ (х ) -2 0 2 х
f ′ (х) min max min
х min = -2, x max = 0, x min = 2.
4) Чтобы определить, где на координатной плоскости находятся экстремумы, нужно найти не только её абсциссу точки, но и ординату. Подставим в функцию абсциссы точек экстремума: у min = 0,25(-2) 4 -2(-2) 2 +5 =1
у max = 0,25(0) 4 -2*0 +5 = 5; у min = 0,25(2) 4 -2(2) 2 +5 =1
Точки экстремумов: т.А(-2; 10), т.В( 0; 5), т. С(2; 2),

4 часть лекции
Уточняющие, дополнительные подсчеты:
Чтобы построить график точнее, находятся нули
функции (точки пересечения графика функции о осями)
а) ось у, точку находим из условия х = 0. (0; f (0)), в
данном случае (0; 5)
б) ось х, точки пересечения находим из условия у = 0 .
0,25х 4 - 2х 2 +5 = 0,- биквадратное уравнение, заменим
х 2 =у, 0,25 у 2 - 2у +5 = 0,
D =4-5= - 1 – нет корней, нет пересечения с осью ОУ.
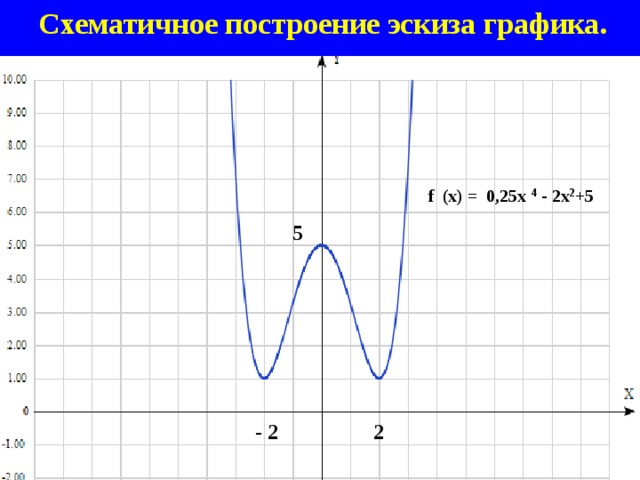
Схематичное построение эскиза графика.
f (х) = 0,25х 4 - 2х 2 +5
5
- 2
2
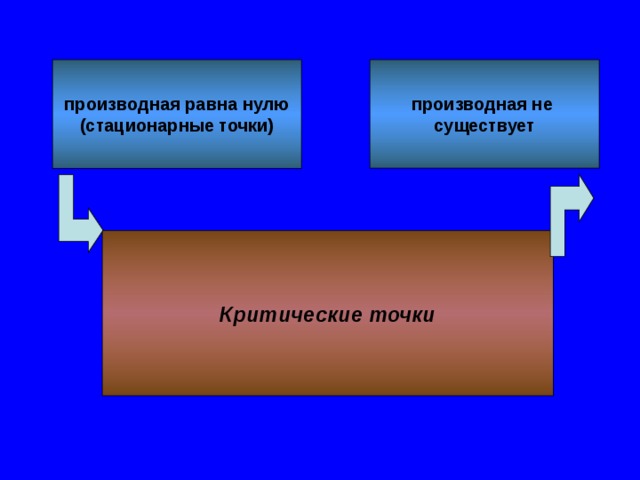
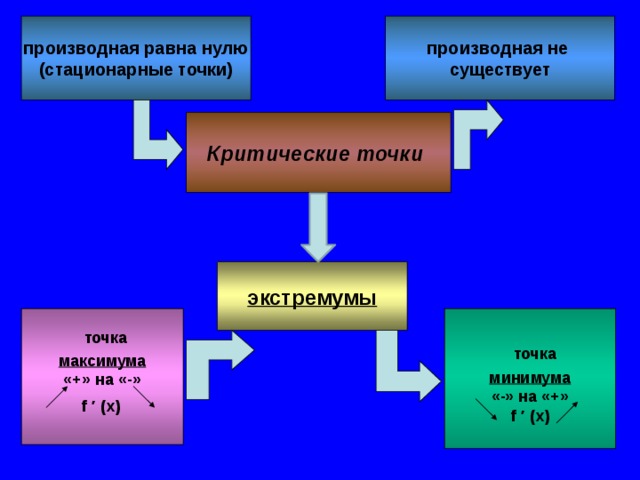
производная равна нулю
производная не
(стационарные точки)
существует
Критические точки
производная равна нулю
производная не
(стационарные точки)
существует
Критические точки
экстремумы
максимума
«+» на «-»
минимума
«-» на «+»
точка
точка
f ′ (х)
f ′ (х)
30
 х 1 , так и f(х 2 ) f(х 1 )? 3. 4. Если функция, определённая на интервале, в каждой точке имеет положительную производную, то данная функция возрастает на этом интервале? да Для убывания дифференцируемой на интервале функции необходимо, чтобы её производная во всех точках интервала принимала отрицательные значения? 5. да да Если функция возрастает в интервале, то угловой коэффициент касательных к графику этой функции в любой точке интервала будет положительным? 6. да Можно ли с помощью производной функции найти максимальное или минимальное значение функции. да " width="640"
х 1 , так и f(х 2 ) f(х 1 )? 3. 4. Если функция, определённая на интервале, в каждой точке имеет положительную производную, то данная функция возрастает на этом интервале? да Для убывания дифференцируемой на интервале функции необходимо, чтобы её производная во всех точках интервала принимала отрицательные значения? 5. да да Если функция возрастает в интервале, то угловой коэффициент касательных к графику этой функции в любой точке интервала будет положительным? 6. да Можно ли с помощью производной функции найти максимальное или минимальное значение функции. да " width="640"
Содержание карточки:
№
Верите ли вы, что…
1.
п/п
Ваше мнение(«+» - да, «-» - нет)
Функция у=х 2 убывает на промежутке [0;+∞)?
2.
нет
Фукция f(х), заданная на интервале, является возрастающей, если, как только х 2 х 1 , так и f(х 2 ) f(х 1 )?
3.
4.
Если функция, определённая на интервале, в каждой точке имеет положительную производную, то данная функция возрастает на этом интервале?
да
Для убывания дифференцируемой на интервале функции необходимо, чтобы её производная во всех точках интервала принимала отрицательные значения?
5.
да
да
Если функция возрастает в интервале, то угловой коэффициент касательных к графику этой функции в любой точке интервала будет положительным?
6.
да
Можно ли с помощью производной функции найти максимальное или минимальное значение функции.
да
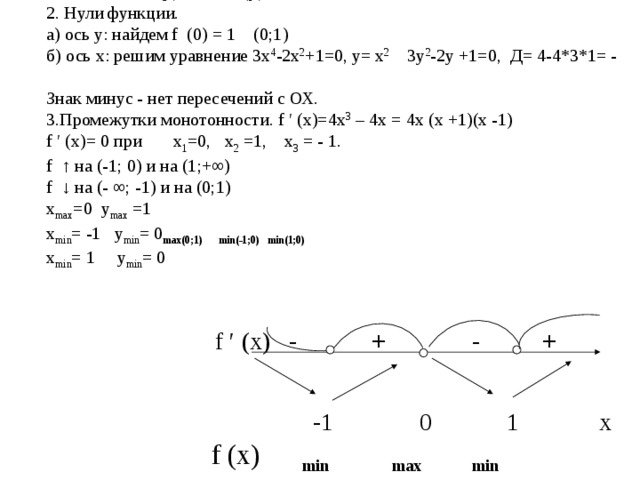
Исследуйте функцию и постройте схематично её график f (х)= х 4 -2х 2 +1
Решение: 1.D(у) = R; E(у) = R
2. Нули функции.
а) ось у: найдем f (0) = 1 (0;1)
б) ось х: решим уравнение 3х 4 -2х 2 +1=0, у= х 2 3у 2 -2у +1=0, Д= 4-4*3*1= -
Знак минус - нет пересечений с ОХ.
3.Промежутки монотонности. f ′ (х)=4х 3 – 4х = 4х (х +1)(х -1)
f ′ (х)= 0 при х 1 =0, х 2 =1, х 3 = - 1.
f ↑ на (-1; 0) и на (1;+∞)
f ↓ на (- ∞; -1) и на (0;1)
х max =0 y max =1
х min = -1 y min = 0 max(0;1) min(-1;0) min(1;0)
х min = 1 y min = 0
-1 0 1 х
f (х) min max min
f ′ (х) - + - +
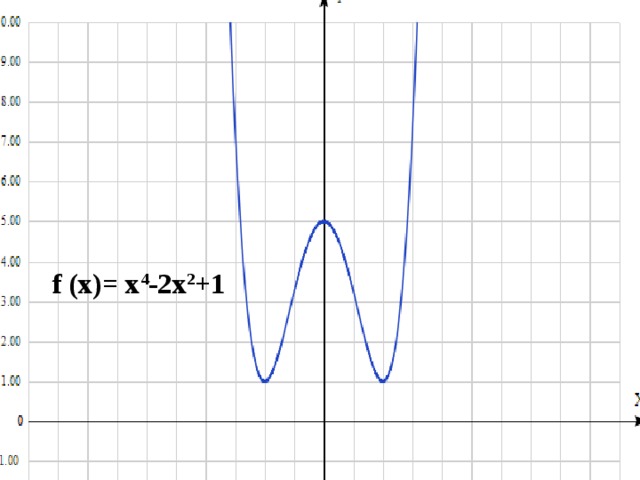
f (х)= х 4 -2х 2 +1

Домашнее задание:
1)Выучить теоретический материал.
2) Решить упражнения: Найдите экстремумы следующих функций:
а) f (х) = 1+4х – х 2 ;
б) f (х) = 3+х 2 – 6х

Спасибо
за урок!










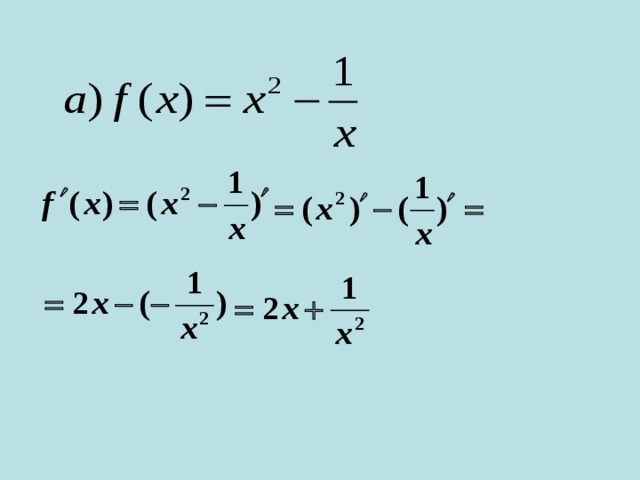
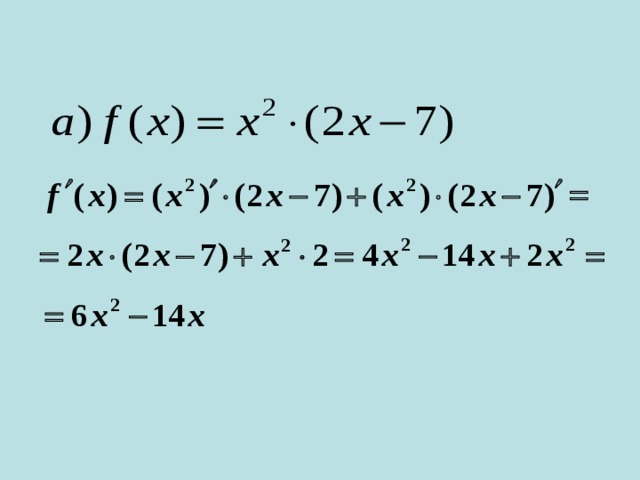
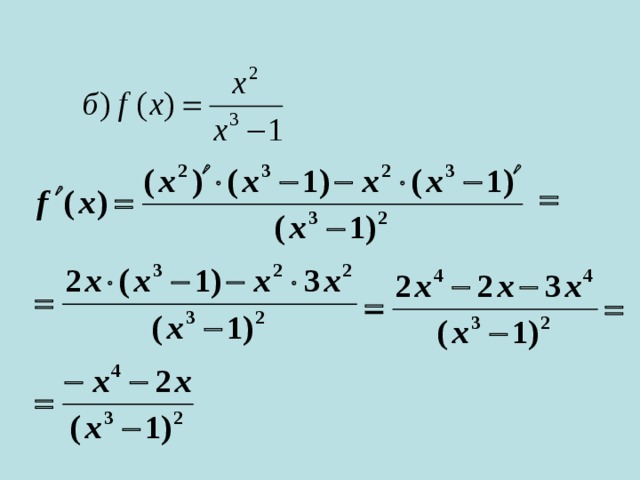



















 х 1 , так и f(х 2 ) f(х 1 )? 3. Если функция, определённая на интервале, в каждой точке имеет положительную производную, то данная функция возрастает на этом интервале? 4. Для убывания дифференцируемой на интервале функции необходимо, чтобы её производная во всех точках интервала принимала отрицательные значения? 5. Если функция возрастает в интервале, то угловой коэффициент касательных к графику этой функции в любой точке интервала будет положительным? 6. Можно ли с помощью производной функции найти максимальное или минимальное значение функции. " width="640"
х 1 , так и f(х 2 ) f(х 1 )? 3. Если функция, определённая на интервале, в каждой точке имеет положительную производную, то данная функция возрастает на этом интервале? 4. Для убывания дифференцируемой на интервале функции необходимо, чтобы её производная во всех точках интервала принимала отрицательные значения? 5. Если функция возрастает в интервале, то угловой коэффициент касательных к графику этой функции в любой точке интервала будет положительным? 6. Можно ли с помощью производной функции найти максимальное или минимальное значение функции. " width="640"

 0. Теорема 2. Функция f (x) убывает на интервале (a; b) тогда и только тогда, когда для любого х из (a; b) f ′ (х) Правило нахождения интервалов монотонности. Находим производную f ′ (х), Находим точки в которых f ′ (х)=0 или не существует. Эти точки называются критическими для функции f . Критические точки разбивают область определения на интервалы, на каждом из которых производная f ′ (х) сохраняет свой знак. Эти интервалы будут интервалами монотонности. Определяем знак f ′ (х) на каждом из найденных интервалов. Если f ′ (х)0 на интервале, то на нем функция возрастает, если f ′ (х) " width="640"
0. Теорема 2. Функция f (x) убывает на интервале (a; b) тогда и только тогда, когда для любого х из (a; b) f ′ (х) Правило нахождения интервалов монотонности. Находим производную f ′ (х), Находим точки в которых f ′ (х)=0 или не существует. Эти точки называются критическими для функции f . Критические точки разбивают область определения на интервалы, на каждом из которых производная f ′ (х) сохраняет свой знак. Эти интервалы будут интервалами монотонности. Определяем знак f ′ (х) на каждом из найденных интервалов. Если f ′ (х)0 на интервале, то на нем функция возрастает, если f ′ (х) " width="640"











 х 1 , так и f(х 2 ) f(х 1 )? 3. 4. Если функция, определённая на интервале, в каждой точке имеет положительную производную, то данная функция возрастает на этом интервале? да Для убывания дифференцируемой на интервале функции необходимо, чтобы её производная во всех точках интервала принимала отрицательные значения? 5. да да Если функция возрастает в интервале, то угловой коэффициент касательных к графику этой функции в любой точке интервала будет положительным? 6. да Можно ли с помощью производной функции найти максимальное или минимальное значение функции. да " width="640"
х 1 , так и f(х 2 ) f(х 1 )? 3. 4. Если функция, определённая на интервале, в каждой точке имеет положительную производную, то данная функция возрастает на этом интервале? да Для убывания дифференцируемой на интервале функции необходимо, чтобы её производная во всех точках интервала принимала отрицательные значения? 5. да да Если функция возрастает в интервале, то угловой коэффициент касательных к графику этой функции в любой точке интервала будет положительным? 6. да Можно ли с помощью производной функции найти максимальное или минимальное значение функции. да " width="640"














