Отношение площадей подобных треугольников

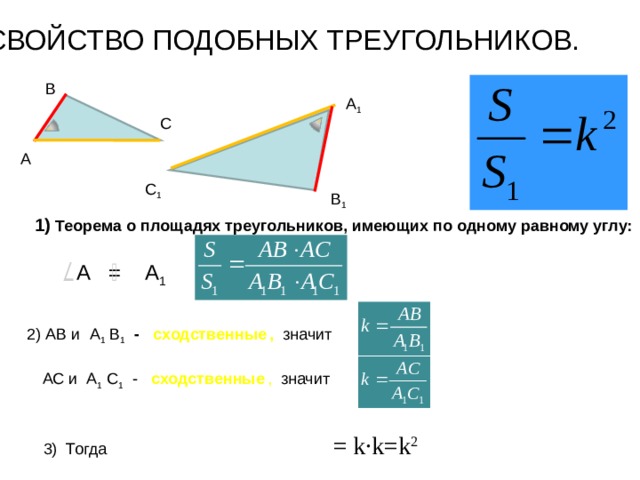
СВОЙСТВО ПОДОБНЫХ ТРЕУГОЛЬНИКОВ.

В

А 1

С

А

С 1

В 1

1) Теорема о площадях треугольников, имеющих по одному равному углу:

А = А 1

2) АВ и А 1 В 1 - сходственные , значит

АС и А 1 С 1 - сходственные , значит

= k∙k=k 2

3) Тогда

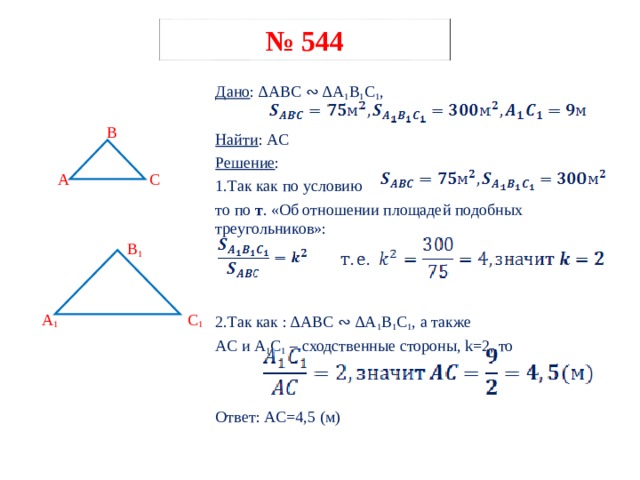
№ 544

B

A C

B 1

A 1 C 1

Дано : ∆ ABC ∾ ∆A 1 B 1 C 1 ,

Найти : AC

Решение :

1.Так как по условию

то по т . «Об отношении площадей подобных треугольников»:

2.Так как : ∆ ABC ∾ ∆A 1 B 1 C 1 , а также

AC и A 1 C 1 – сходственные стороны, k=2, то

Ответ: AC =4,5 (м)

Реши задачи

• Две сходственные стороны подобных треугольников равны

8 см и 4 см. Периметр второго треугольника равен 12 см.

Чему равен периметр первого треугольника ?

24 см

2. Две сходственные стороны подобных треугольников равны

9 см и 3 см. Площадь второго треугольника равна 9 см 2 .

Чему равна площадь первого треугольника ?

81 см 2

3. Две сходственные стороны подобных треугольников равны

5 см и 10 см. Площадь второго треугольника равна 32 см 2 .

Чему равна площадь первого треугольника ?

8 см 2

4. Площади двух подобных треугольников равны 12 см 2 и 48 см 2 .

Одна из сторон первого треугольника равна 4 см. Чему равна

сходственная сторона второго треугольника ?

8 см

Задание для самоподготовки

• П.58, 59, 60 повторить
• выполнить №545, 548